无人机GNSS辅助光束法平差最佳摄站权值探索

李 飞，袁 凯，张 超

(济南市勘察测绘研究院，山东 济南 250101)

近年来，无人机的快速发展为遥感信息获取提供了新方法，它可以有效弥补卫星影像受平台、周期和分辨率上的不足。在无人机遥感逐渐成为国防战略和经济建设关键技术的同时，其在小范围高精度测绘、应急作战保障、灾害紧急救援等方面发挥着不可替代的作用[1]。

利用无人机影像实现地理环境监测和应急预案制定，地面目标的精确定位始终是首要考虑的问题[2]。从目前技术发展来看，影像对地定位技术主要包括摄影测量学科和计算机视觉学科两大方面[3]，但本质上两者均是对未知参数的估值问题，即所谓的光束法平差，其中摄影测量的空中三角测量是以物点、摄影中心、像点构建的共线条件方程为基本平差单元，解算过程会出现误差方程数量多，计算结果受初值和粗差影响较大，而计算机视觉的运动恢复结构技术则是通过齐次坐标建立三维世界与二维影像的映射关系，依靠矩阵运算的方式求解最大似然估值，具有良好的抗差能力，且计算效率更高[4]，是目前主流商业软件所采用的核心技术。

在差分GNSS模块微型化发展的今天，差分型无人机已占据了大部分市场，其厘米级的高精度动态定位优势备受各界关注。国外部分学者验证了应用RTK无人机直接进行地理定位，可以实现分米级的测量精度，可有效应用于三维快速成图[5]；还有部分学者应用四旋翼无人机搭载差分板卡，最后以少量控制点实现了地面目标的厘米级定位精度，进而生产了数字正射影像图[6]。国内的部分研究人员也给出了不同型号的差分型无人机配合计算机视觉的SFM技术可大大提升定位精度，降低对地面控制点的依赖[7]。事实上，在光束法平差过程，差分型无人机可以提供精度较高的外方位线元素初值，但一般情况下，差分GNSS系统的理论测量精度是静态条件下的测试结果。因此，如何确定GNSS观测值的权重，将是影响光束法平差结果好坏的关键因素。本文以计算机视觉的运动恢复结构技术实现影像对地定位，重点讨论摄站坐标权值对定位精度的影响，通过对最佳权值的探索，降低对地面控制点的依赖，进而实现优化定位精度的目的。

1 精确摄站约束下的光束法平差

一般情况下，我们以像点实际坐标和观测坐标构成的重投影误差作为衡量定位精度的指标。光束法平差即是令重投影误差最小，进而求得最大似然估值[8]。本文应用差分型无人机获取的高精度摄站坐标实现投影矩阵计算，进一步得到影像外方位元素、相机参数和地面坐标。设影像数量为n，对应地面的像点m个，地面点Mi(i=1,2,…,m)对应影像j(j=1,2,…，n)上的像点为mij，影像j的投影矩阵为Pj，则光束法平差的约束条件可表示为：

(1)

式中，wij为像点可见性函数，若Mi在影像j上可见时，取值为1，不可见时取值为0；Q(Pj,Mi)为由地面点坐标Mi(i=1,2,…,m)经投影变换Pj得到的像点坐标，若令PjMi=[(PjMi)1(PjMi)2(PjMi)3]T,则像点坐标的计算值可表示为：

(2)

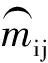
(3)

s表示影像的畸变参数，因此，在未知参数初值的邻域内，即可将观测方程线性化处理，得到一阶误差方程式：

VX=Bx+AXt+Ss-LX,WM:E

VG=AGt-LG,WM:PG

VI=AIt-LI,WM:PI

(4)

式中，VX、VG、VI分别为像点、摄站以及影像姿态角改正数向量；E、PG、PI为权重矩阵；x为物点坐标增量向量；t为影像位姿参数增量向量；s为相机畸变参数向量；B、AX、S、AG、AI为观测值的系数矩阵；LX、LG、LI分别为像点坐标残差、摄站坐标残差和姿态角残差向量。

对误差方程实现最小二乘平差计算，即可获取待求目标点的三维坐标信息。

2 GNSS辅助空中三角测量的定权研究

2.1 观测值权值对定位精度的影响

以多种观测值构成的联合平差中，权值的确定方法往往会对平差计算结果产生很大影响，若权值在定义时存在误差，待求参数在平差解算后仍然满足无偏要求，但此时单位权方程却是有偏的，进而影响到待求参数的协因数矩阵。

设某平差模型如下：

E(l)=BX,D(l)=σ2P-1

(5)

其中P为观测值权矩阵，根据最小二乘运算法则，可用下式表示待求参数的估值和相应的协因数矩阵：

(6)

(7)

一般情况下，在平差解算过程未考虑最佳权值时，权值包含某误差ΔP，记为

(8)

则实际待求参数的估值和相应的协因数矩阵可表示为：

(9)

(10)

N-1ΔNN-1ΔNN-1

(11)

因此，结合式(6)、(9)、(10)、(11)，可以有效获取待求参数的实际估值：

(12)

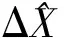
(13)

因此，理论和实际的平差模型可分别表示如下：

(14)

(15)

综合以上分析，平差模型的解算精度在一定程度上受权值影响比较大。要获得高精度参数估计，必须保证权值具有一定的合理性，降低权值误差。因此，对于无人机GNSS辅助光束法平差，合适的权值设定是提高对地定位精度的关键因素。

2.2 摄站坐标的定权方法

区别于传统依靠地面控制点的空中三角测量，本文以精确摄站坐标为主要控制依据，因此差分GNSS所测坐标的权值成为了平差解算精度的关键。我们知道，观测值方差往往可以作为表示精度的一个指标，且与观测条件的误差相对应，故各观测值方差的比值同样可以作为衡量精度的指标，可将其设为权[10]。

由于差分型无人机的动态定位精度受飞行速度、飞行距离、信号接收等情况影响，因此，对于不同飞行任务，摄站坐标的获取精度均存在差异性，下文将结合实验，设置一定精度范围，改变摄站坐标权值，将不同权值约束下的平差计算值与检查点实测结果进行比较，进而得到最佳的摄站坐标权值，实现优化定位的目的。

3 实验与分析

3.1 实验数据

实验选取某测区2 km2范围，采用某差分型固定翼无人机，搭载索尼RX1RII数码相机实施航摄飞行，其中布设航线10条，采集航向重叠80%、旁向重叠60%的影像247幅，布设控制点18个，检查点16个。任务区域和航线布设形式如图1所示，控制点和检查点坐标如表1所示。

图1 任务区和航线布设形式

表1 控制点和检查点坐标/m

3.2 光束法平差的摄站权值探索实验

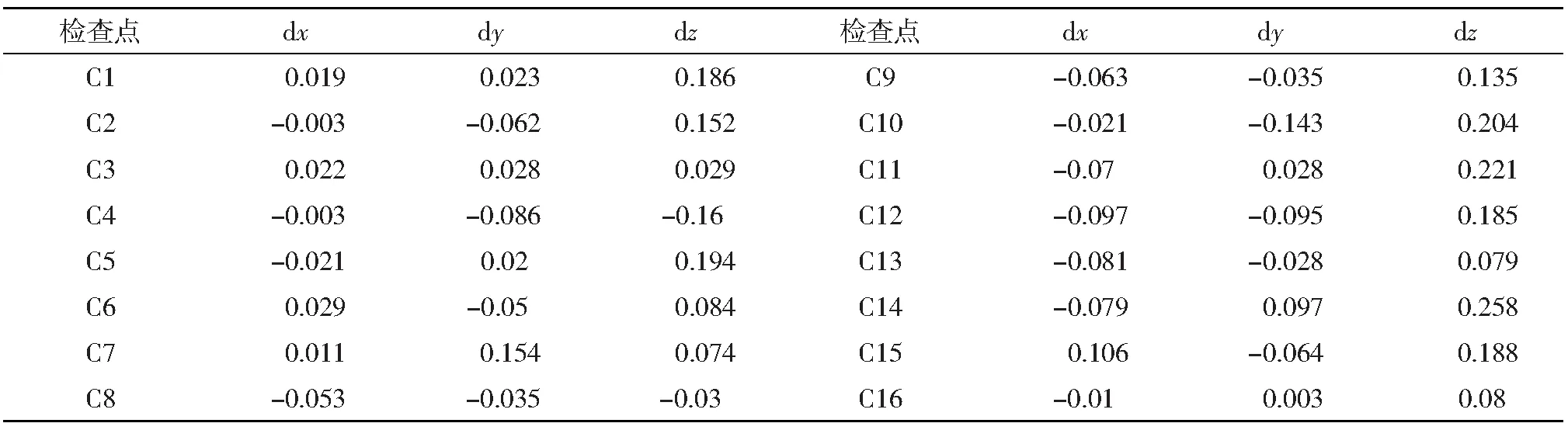
表2 σG=0.01 m检查点反投影误差/m

图2 σG=0.01 m检查点的计算精度

σG取值为0.05 m进行平差，检查点的反投影误差如表3所示，计算精度统计结果如图3所示。

表3 σG=0.05 m检查点反投影误差/m

图3 σG=0.05 m检查点的精度

σG取值为0.1 m进行平差，检查点的反投影误差如表4所示，计算精度统计结果如图4所示。

图4 σG=0.1 m检查点的精度/m

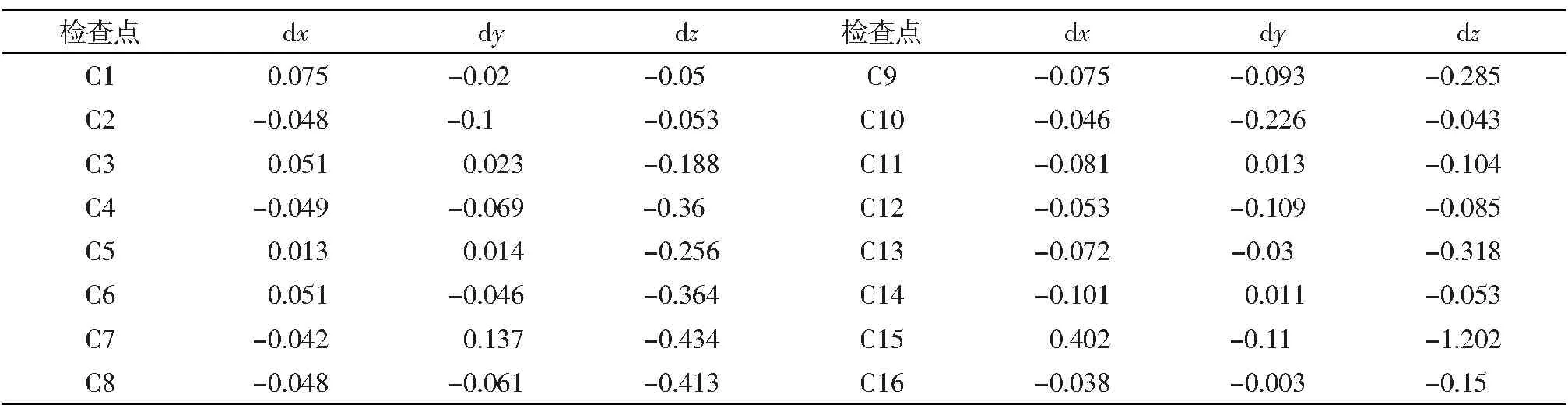
表4 σG=0.1 m检查点反投影误差/m

σG取值为0.2 m进行平差，检查点的反投影误差如表5所示，计算精度统计结果如图5所示。

图5 σG=0.2 m检查点的精度

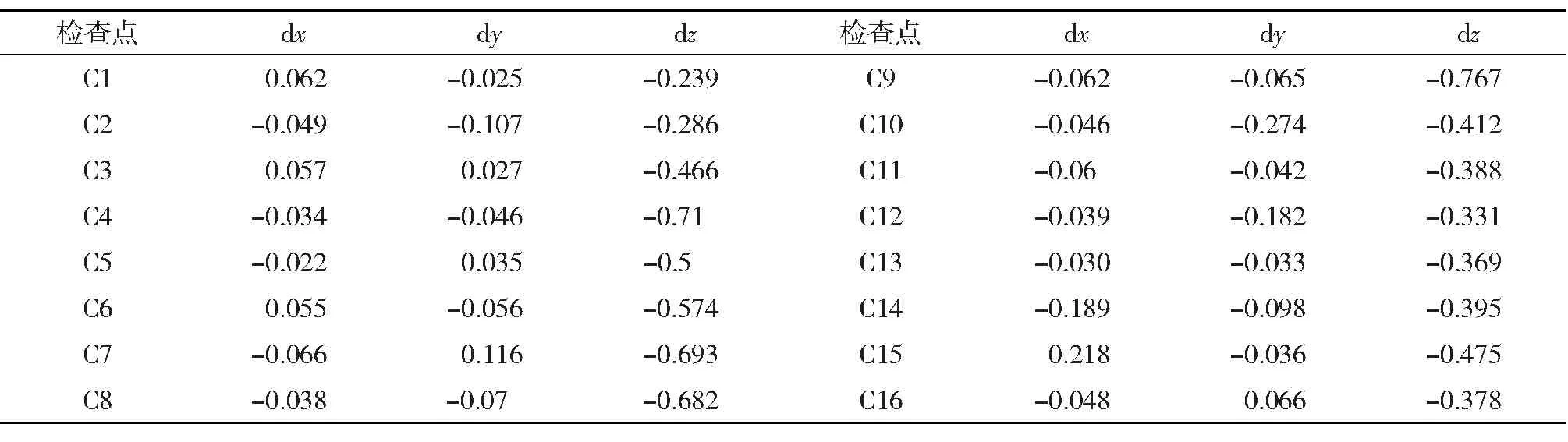
表5 σG=0.2 m检查点反投影误差/m

由图6可知，随着σG取值的增加，检查点的中误差呈现先减小后增加的趋势，其中，σG取值的不同对水平方向的定位误差影响不大，但对高程方向的定位误差影响显著。经比较分析，当σG=0.05 m时，可获取摄站坐标的最佳权值，此时中误差在水平和高程方向均取得最小值，即mxy=0.107 mm，mz=0.149 mm。

图6 不同权值的中误差统计

3.3 对地定位优化实验

在GNSS辅助空中三角测量过程中，经最佳摄站权值的探索，为光束法平差提供了精度优化的依据。为进一步探索本文对地定位的优化效果，在GNSS辅助光束法平差(GNSS BBA)过程中，分别引入0个、2个、4个和6个控制点参与平差解算，与18个控制点参与的平差(GCP BBA)定位进行比较，得到中误差计算结果如表6所示。

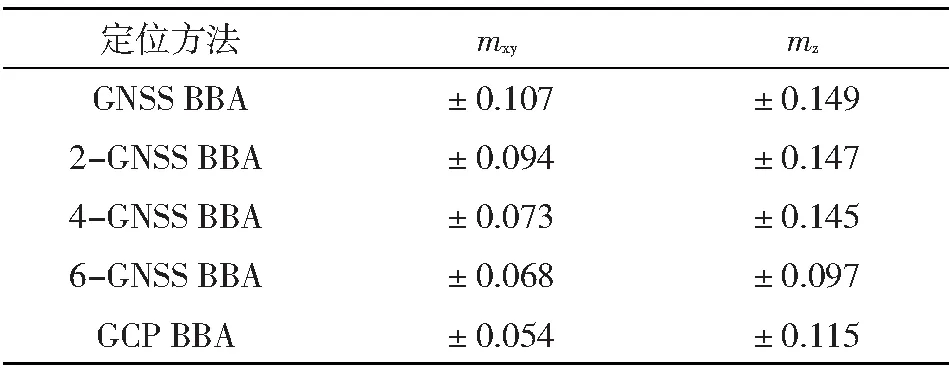
表6 对地定位精度统计/m

可见，本文GNSS辅助光束法平差过程中，通过引入少量的地面控制点，使得对地定位精度得到进一步提升。就本文实验而言，当引入6个地面控制点时，高程方向的定位精度提升显著，且和18个控制点参与的平差定位精度相当，甚至在高程方向还具有一定的优势。

3.4 实验总结

本文首先在GNSS辅助光束法平差过程中，通过统计不同摄站精度条件下检查点的误差分布，比较分析出了最佳摄站权值，即σG=0.05 m所对应的权值，在该权值约束下，对地定位精度得到了大幅度提升。随后，为验证本文方法在减少地面控制点方面的优势，分别引入了不同数量的地面控制点参与平差解算，结果发现，最佳摄站条件下的GNSS辅助光束法平差配合6个地面控制点，定位精度与18个控制点参与的平差定位效果相当。

4 结 语

本文为充分发挥差分型无人机的高精度动态定位优势，在GNSS辅助光束法平差过程中，提出了最佳摄站坐标权值参与平差的优化方法。实验结果表明，差分型无人机对地定位精度与平差解算过程权值的设定密切相关，最佳的摄站权值配合少量的地面控制点参与光束法平差，可以达到大量控制点参与的平差定位精度。可见，本文方法可以有效降低GNSS辅助光束法平差对控制点的依赖，对减少外业工作量、提高工作效率具有促进作用。但本文仅研究了摄站坐标的最佳权值，对平差过程其他观测量的权值缺少讨论。在下一步研究中，需要打破传统的定权方式，将最佳权值的确定融入到估值算法中，建立更佳完善的平差模型。