纤维增韧陶瓷基复合材料热端部件的热分析方法现状和展望
赵陈伟,毛军逵,2,*,屠泽灿,邱鹏霖
1.南京航空航天大学 能源与动力学院,南京 210016
2.南京航空航天大学 江苏省航空动力系统重点实验室, 南京 210016
早在20世纪50年代,陶瓷材料就以其耐高温、密度小等优点,受到研究人员的青睐。从那时起,人们就开始尝试在航空燃气涡轮发动机、冲压发动机、火箭发动机等先进推进系统中使用陶瓷材料[1]。传统陶瓷材料的机械性能难以满足热端部件的高载荷等工作要求,这使得陶瓷材料在这些先进推进系统中的实际工程应用受到阻碍。随着Aveston[2]在20世纪70年代初,提出纤维增韧陶瓷基复合材料(Ceramic Matrix Composite,CMC)的概念,CMC材料中纤维增韧大大改善了陶瓷材料的机械性能,使得其在高热负荷和高机械负荷下的实际工程应用成为可能。
自CMC材料问世以来,美、俄等航空航天大国,包括日本等新兴科技强国先后出台多个研发计划[3-7]对CMC材料进行研发,尤其为CMC热端部件在航空发动机等高性能动力装置中的工程应用提供了大量的支持。如美国政府主导的“综合高性能发动机技术IHPTET(Intergraded High Performance Turbine Engine Technology)”计划、“超高效发动机技术UEET(Ultra Efficient Energy Technology)”计划等,日本政府主导的“下一代超音速环境兼容推进系统的研究与开发ESPR(Research and Development of Environmentally Compatible Propulsion System for Next Generation Supersonic Transport)”计划,俄罗斯政府主导的“国家技术基础2007—2011”计划中均有专项经费用于CMC热端部件的研发。在上述计划的支持下,这些国家的CMC材料应用发展迅速。
经过多年的研发,整体成形的CMC热端部件得到越来越多的航空发动机制造厂商的青睐[8-10],CMC热端部件已逐渐在航空燃气涡轮发动机的转/静子部件上得到工程应用。2004年,GE(General Electric Company)和Allison联合开发并验证了空心CMC材料高压涡轮导向器叶片,该叶片质量比镍基高温合金导向器叶片减少50%[7]。2009年GE宣布,F136发动机的第三级低压涡轮导向叶片采用了CMC叶片[11]。在C919客机上采用的LEAP-X发动机,其高压涡轮一级外环、低压涡轮导向叶片以及尾锥等核心热端部件也均采用了CMC材料[12]。2015年,GE公司网站披露,GE公司研制了世界首个CMC低压涡轮转子叶片,并在F-414发动机的验证机上成功通过了500个严酷循环测试[13]。GE公司认为上述CMC涡轮导向叶片和转子叶片的成功研制,为GE公司与美国空军研究试验室合作开展下一代自适应发动机的研制奠定了基础;同时其为实现相比当今第五代发动机燃油消耗量降低25%、最大推力提高10%的目标提供了关键技术支撑[14]。
尽管CMC材料的安全使用温度可达 1 923 K左右[15-16],但在未来推重比为 12~15 的航空涡轮发动机中燃烧室出口燃气温度高达 2 100~2 300 K[2],而在火箭发动机以及使用火箭基组合循环推进系统的高超声速飞行器发动机中燃气温度更是高达 2 400~3 600 K[17]。显然未来先进动力装置热端部件的工作温度仍远超过了CMC材料所能承受的温度极限。
高温环境下,CMC材料中的SiC或C增韧纤维及SiC基体会发生氧化反应。事实上,目前CMC材料,除SiC基体外,已经发展出了多种基体材料。但与SiC基体在高温环境下会发生氧化反应相同,ZrB2-SiC-ZrC[18]、Si-C-N[19]、CVD-Si3 N4[20]以及SiBCN[21]等多种基体材料在高温环境下也存在氧化问题。本文重点归纳和分析了以SiC为基体的CMC材料导热系数预估及热端部件热分析方法。
GE公司[22]研究表明采用Hi-Nicalon纤维增强的CMC材料在1 200 ℃ 的空气中暴露4 000 h后,极限强度退化小于10%,而在1 315 ℃ 的空气中暴露1 000 h后,极限强度退化就高达30%。Unal等[23]对SiC/SiC复合材料的研究表明,SiC/SiC复合材料试样暴露于1 400 ℃ 的干燥氧气环境中50 h后,氧化试件的断裂应力下降约50%。同时高温环境下高温度梯度导致的热应力也会对CMC热端部件的结构可靠性构成威胁。因此,为了防止CMC热端部件在实际工程应用时超温发生氧化和产生过高的热应力,需要在CMC材料热端部件设计分析时准确预估其温度场。为此,建立高精度的CMC热端部件热分析方法就显得尤为重要。
从基础的导热系数热物性预估来看,CMC材料作为纤维增韧复合材料的一种,其增韧纤维的微观结构特性会使得增韧纤维的轴向与径向的导热系数存在明显差异[24-26], 进而使得CMC材料导热系数具有明显的各向异性[27-30]。Tian和Kevin[25]通过试验测试了碳纤维增韧树脂基复合材料的等效导热系数(Equivalent Thermal Cond-uctivity,ETC),结果显示沿纤维方向和垂直纤维方向的等效导热系数分别为6.316 W/(m·K)和0.611 W/(m·K),两者相差10.3倍。
同时,CMC材料内部非均质的结构特征,如其内部纤维束的排布和编织方式等,使得CMC导热系数各向异性特征具有显著的结构效应[31-33]。此外CMC材料导热系数各向异性与热端部件空间扭曲型面之间的耦合作用、气膜冷却热防护措施下气固耦合传热以及由于加工工艺等带来的物性分散度,都给CMC热端部件的热分析带来新的挑战[30-35],因此亟待发展针对CMC热端部件的各向异性导热系数预估方法、热分析模型和相应的分析方法。
本文主要归纳了不同编织方式(单向纤维、2/2.5维编织、3维编织)下CMC材料导热系数预估方法的研究进展,阐述了考虑CMC热端部件结构特征下其热分析方法的研究现状,重点剖析了目前CMC热端部件在气固耦合热分析时面临的挑战,展望了未来CMC热端部件高精度热分析的发展方向。
1 CMC材料各向异性导热系数的预估方法
在对CMC热端部件进行热分析时,CMC材料各向异性导热系数的准确预测是对其进行温度场计算模拟的核心问题之一。CMC材料由于内部编织结构的不同,其各向异性导热系数预测模型也不尽相同。就纤维编织方式而言,目前CMC材料主要分为3类,如图1所示。
第1类由单向增韧纤维和陶瓷基体复合得到,属于单向纤维增韧复合材料(Unidirectional Fiber Reinforced Composites,UFRC)中的一种,如图1(a)所示[36-37]。这类材料结构简单,便于加工和制造,增韧纤维在基体中单向布置。UFRC在纤维增韧方向上有较好的机械性能,而在垂直于纤维增韧的方向上抗剪切能力较弱。第2类是2/2.5维(2/2.5D)纤维编织CMC,属于2/2.5D纤维编织复合材料(Two/Two Point Five Dimensional Weave Composites,TDWC)中的一种,这类材料与第1类材料相比而言,其机械性能得到提高,具有较为理想的剪切性能以及层间性能,在航空、航天、船舶等行业的应用前景十分广泛[36-37],如图1(b)和图1(c)所示[38]。第3类是3维纤维编织CMC材料,属于3维纤维编织复合材料(Three Dimensional Braided Composites,TDBC)中的一种,如图1(d)所示[39-40]。目前TDBC已经大量应用于先进推进系统中的耐高温、耐磨损构件(如发动机涡轮叶片、喷管、燃烧室内衬等[41-45]),抗冲击、抗疲劳构件(如航空发动机包容机匣、静子叶片等[44,46])。
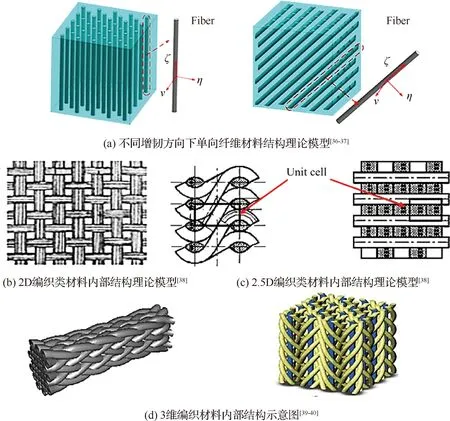
图1 典型纤维增韧CMC材料纤维结构示意图
目前CMC材料导热系数的预估方法主要分为两种。一种是通过建立CMC材料热阻网络模型来求解CMC材料等效导热系数的工程数学计算方法;另一种是通过建立反映CMC真实结构特征的物理模型,结合数值仿真的方法对CMC等效导热系数进行预估。
前者首先根据CMC材料内部结构特征建立不同热阻网络模型,然后根据不同方法对建立的热阻网络模型进行求解,得到CMC材料的等效导热系数。这种方法对内部结构简单的CMC材料有着较好的计算精度,可以帮助工程设计人员快速得到CMC材料的各向异性等效导热系数,常用于单向纤维增韧CMC材料以及部分2维编织CMC材料的导热系数预测中,而将这种方法应用于内部编织结构复杂的2.5D以及3D纤维编织CMC材料时则会造成较大的预测误差。
后者的关键在于建立能够反应CMC材料真实内部结构特性的模型。RVE(Representative Volume Element)方法是目前最常用的方法之一。该方法最先由Hill[47]提出,其认为RVE是一个取样单胞,首先它在结构上对整体复合材料具有完全的代表性,其次需要包含足够数量的内部特征结构以保证得到的等效模量可以代表复合材料整体的宏观模量。具体到等效导热系数预估方面,RVE方法是先建立一个微观结构的代表性单胞,然后基于该单胞,采用有限元等方法求解能量守恒方程,最后根据傅里叶定律求得材料的等效导热系数。
随着学者们对CMC材料导热系数预估方法研究的深入,发现CMC材料的内部结构特征愈发复杂多样,包含有微观/细观/宏观三个不同尺度的结构特征。如何在构建RVE模型时兼顾材料的微观和宏观结构特征是准确预测CMC材料等效导热系数的关键问题,同时RVE模型还要兼顾当下计算机的计算能力以及计算速度,因此选取合理的代表性单元十分重要。
20世纪70年代开始发展的均匀化方法(Homogenization Method)和多尺度渐进分析方法(Multi-scale Asymptotic Analysis)为RVE模型的构建提供了指导思想[48-50]。均匀化的方法可以在一定程度上简化模型,而多尺度的方法可以帮助研究人员考虑不同尺度的结构特征对CMC材料等效导热系数预测的影响。
本节分别针对单向纤维、2/2.5维纤维编织以及3维纤维编织三类编织结构的CMC材料,总结分析其导热系数预测的研究进展。
1.1 UFRC 单向长纤维增韧复合材料
早期学者对UFRC等效导热系数的预测模型建立在如下理想假设的基础上:① 基体和增韧纤维皆为均质材料;② 基体与纤维完全接触,且纤维在基体中周期排布;③ 在该计算模型中纤维的截面形状为圆形或者矩形;④ 材料不存在裂纹或者孔隙。
工程数学计算模型首先需要构建合理的热阻网络,而后通过热阻网络来求解热传导方程,最后得到UFRC的等效导热系数。Thornburg和Pears[51]针对具有离散增强相的塑料复合材料,构建了串/并联热阻网络求解模型,并成功计算得到该材料的等效导热系数。在此基础上,Springer和Tsai[52]采用等效电阻法建立了针对UFRC等效导热系数预测的工程数学计算模型。Zou等[53]采用热电类比法求解热阻网络,成功推导了UFRC横向等效导热系数的数学计算公式,并通过其构建的“C-S”和“E-S”单元模型分析了不同纤维体积分数、导热系数比和不同纤维截面(椭圆形和方形)对UFRC等效导热系数预测的影响。Faleh等[54]采用热阻网络法与数值仿真相结合的方法,建立了纤维周期叉排时的工程数学计算模型。研究中采用线性回归的方法,在不同线性回归决定系数下拟合得到了3个用于UFRC等效导热系数预测的工程数学计算公式。
上述UFRC导热系数计算方法都建立在理想化模型的基础上。虽然这些模型能够对UFRC的等效导热系数进行初步预估,但是无法反映真实微观结构特征,因此预估精度仍有限。
随着扫描电子显微镜(Scanning Electron Microscope,SEM)等微观测试设备的发展,Hasselman等[55]获取了UFRC更多的微观结构特征,例如增韧纤维在空间分布上具有随机性,纤维与基体并非完全接触,两者之间存在界面以及基体材料存在裂纹和孔隙等,如图2所示。
在考虑UFRC的真实微观结构特征后,许多研究学者重点针对增韧纤维在空间分布的随机性、界面热阻以及裂纹和孔隙,提出了多种导热系数预测的修正方法。
1.1.1 界面热阻的引入和修正
在真实的UFRC中,增韧纤维与基体材料之间存在界面热阻。界面热阻主要包括增韧纤维与基体脱离形成的孔洞、粘接纤维和基体的热解碳界面层等。界面热阻会使得UFRC的等效导热系数降低,尤其是对横向导热系数有显著影响,研究表明界面热阻的存在会使得UFRC的横向等效导热系数减少50%~70%[33]。目前已建立多种针对存在界面热阻时UFRC等效导热系数预测的修正计算模型,如Hasselman模型[56]、Markworth模型[57]和Zou模型[58]。以上3个模型都假设在圆形纤维与基体间存在完整的圆环形界面热阻,在计算时需已知界面热阻的等效传热系数,并且等效传热系数各向同性。当界面热阻的等效传热系数大于 107W/(m2·K) 时,Hasselman模型的预测结果较好;反之,则Markworth模型的预测精度更高。
文献[59]中的研究结果显示界面热阻的等效导热系数值分布范围广且各向异性,难以确定一个合理的值带入计算模型中。Youngblood模型[60]在以上3个模型的基础上初步考虑了界面热阻的导热各向异性对UFRC等效导热系数预测的影响。
上述模型虽然考虑了界面热阻对等效导热系数预测的影响,但这些模型都假设纤维与基体完全脱开,即纤维与基体间存在一个规则的圆环或矩形柱体的界面热阻,如图3(a)和图3(b)所示[53,60]。但是在实际材料中,纤维与基体间的界面热阻并不是完整的圆环结构,且界面热阻的形貌对UFRC等效导热系数有影响[61],如图2所示。为解决这个问题,Klett等[62]建立了界面热阻非规则分布的RVE模型,采用数值仿真的方法来预估等效导热系数,如图3(c)所示。

图3 含界面热阻的计算模型示意图
目前对UFRC等效导热系进行预测时,主要将界面热阻看作除纤维与基体外的第三相物质[63]。将界面热阻简化为完整包围纤维的薄层结构,通过调整界面热阻的换热系数来模拟不同特征参数下界面热阻对ETC的影响。这种将薄层对传热的影响等效为接触热阻,并将其作为边界条件直接施加到计算模型的方法,避免了对窄小间隙区域的建模与网格划分操作。该方法已被一些商业CFD和FEA软件所采用,用以对间隙厚度范围为0.1~2 μm的UFRC等效导热系数进行预估[63]。
1.1.2 裂纹和孔隙特征的引入和修正
由于CMC材料的制造工艺,使得CMC材料在制造完成后会存在离散分布的孔隙和裂纹[64-65]。虽然离散分布的孔隙与裂纹的尺度都较小,但在大气环境中其填充物为导热系数极小的空气,这使得微小的孔隙和裂纹也能够形成较大的接触热阻,严重阻碍基体的热传递,从而降低CMC材料ETC。因此考虑孔隙和裂纹缺陷的影响,也是提高ETC预估精度的一个重要研究方向[66]。
Hasselman[67]针对材料中存在的随机裂纹、与热流方向垂直的定向裂纹以及与裂纹平面平行的热流裂纹3种裂纹,推导了3种用于计算UFRC中存在不同类型裂纹时的等效导热系数计算公式。Whittaker等[68-70]对单向纤维增韧C/C复合材料热物性进行了系统研究,该研究基于UFRC的微观结构特征,给出了UFRC中裂纹和孔隙分布特征,如图4所示[69]。随后在考虑这些特征的情况下,建立其横向导热系数预估数学模型。
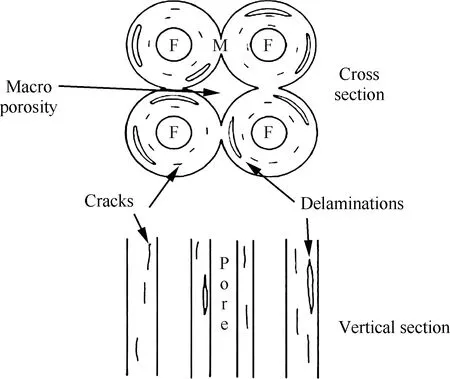
图4 UFRC中孔隙及裂纹示意图[69]
Hasselman和Johnson[56]首次建立了存在分散孔隙的UFRC横向热导系数预测Hasselman-Johnson等效介质模型,该模型目前已成为预测复合材料的横向热导系数应用最广泛的模型之一。Al-astrabadi等[71]利用了UFRC的串/并联热阻网络,建立了包含孔隙特征的RVE模型,计算了UFRC的等效导热系数,并采用线性回归的方法,在不同孔隙比、体积分数比下拟合得到了不同的经验公式。随后Krach和Advani[72]建立了包含不同孔隙形状的RVE模型,来探索孔隙形状对UFRC等效导热系数的影响。研究结果表明,孔隙对材料ETC的影响不能仅用孔隙率(孔隙体积与材料总体积之比)来描述。孔隙的形状和分布情况都对等效导热系数有影响。Krach和Advani建立的有限元分析模型虽然能考虑孔隙形状对等效导热系数的影响,但在其建立的模型中,孔隙穿透了整个基体材料,且对孔隙尺寸以及随机分散的考虑不足,同真实分布存在较大偏差,如图5(a)所示。
为解决这一问题,Yan等[73]基于ANSYS软件,利用蒙特卡洛方法建立了考虑孔隙随机分布的三维数值仿真RVE模型,如图5(b)所示。通过数值和试验数据的比较,证明了该方法的有效性和准确性,数值仿真模型计算得到的ETC与试验值相比其误差仅为2%。
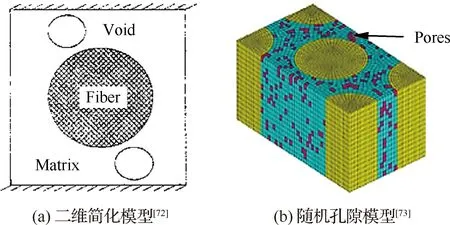
图5 考虑孔隙的RVE模型
1.1.3 随机分布特征的引入和修正
以上针对UFRC等效导热系数的预测方法,无论是工程数学计算的方法还是数值仿真的方法,在预测时都假设纤维在基体中周期分布。而在真实的UFRC中,纤维在基体中是随机分布的,如图2所示。纤维随机分布会影响到材料内部的热量传递特征以及等效导热系数的分布,为此不少学者在建立RVE模型时,引入了纤维随机分布的结构特征。
Mansilla[74]在对UFRC的力学特性进行研究时,应用随机函数控制纤维的位置,建立了纤维随机分布的力学分析RVE模型。研究结果表明,考虑了纤维随机分布特征的RVE模型与纤维周期分布的RVE模型模拟得到的应力分布之间存在明显的差异。相对于纤维周期分布的RVE模型,基于纤维随机分布的RVE模型计算获得的最大应力值和应变值分别提高了60%和36%。Ganapathy等[75]同样建立了一个增强相随机分布的RVE模型,用以计算氧化铝纤维增韧树脂基复合材料的宏观等效导热系数。Graham和Mcdowell[76]在Hasselman-Johnson模型的基础上,用有限元方法对含有随机纤维分布的UFRC横向等效导热系数进行了数值计算。其研究结果表明,UFRC的ECT不仅仅由增强相和基体的体积分数决定,而且还受到微观结构非均匀性程度的影响。
近年来Jiang等[77]学者采用蒙特卡洛方法,研究了纤维随机分布对等效导热系数预估的影响。他们的研究表明,在纤维随机分布的影响下,UFRC的ETC预测结果不再保持一致,而近似服从正态分布。这表明,在实际工程应用中,UFRC的不同部分或不同批次可能会具有不同的ETC。
经过多年的研究,目前针对单向增韧复合材料稳态等效导热系数预测的方法已经较为成熟,为分析单向纤维材料的热量传输机理以及温度分布奠定了基础,同时也可为2D、2.5D和3D编织纤维束的等效导热系数预估提供相应的技术支撑。
1.2 TDWC 2/2.5维纤维编织复合材料
与UFRC相似,早期学者为建立TDWC的等效导热系数的理想数学计算模型,对TDWC提出了如下理想假设:① 基体和编织纤维皆为均质材料;② 基体与编织纤维完全接触,且纤维在基体中周期排列;③ 材料中不存在裂纹或者孔隙。在以上假设条件下,Vishnevskii和Shlenskii[78]建立了一种包含连续重复单元的导热系数预估模型,得到了一种TDWC等效导热系数的计算方法。但是Vishnevskii模型忽略了横向纱线和周围的基体材料,其理论计算结果与有限元分析结果和试验值有较大偏差。Ismail等[79]通过等效元件法建立了TDWC的传热数学模型。该方法先将不规则的纤维以及编织纤维干涉的部位,用规则形状的等效热阻元件替代,再用这些等效热阻元件建立热阻网络,最后通过傅里叶定律求解得到其等效导热系数,如图6所示。

图6 Ismail等效元件模型[79]
Ismail模型虽然能够预测TDWC的等效导热系数,但是该模型忽略了材料编织结构参数对等效导热系数预测带来的影响。Ning和Chou[80]考虑TDWC的编织结构参数,基于热阻网络法,建立了计算TDWC横向等效导热系数的3维热阻网络传热分析模型,如图7所示。虽然研究中考虑了材料编织结构参数带来的影响,但是其模型假设编织纬纱与经纱截面为矩形,且忽略了经纱与纬纱之间的接触热阻。Dasgupta等[81]同样采用热阻网络法,建立了更能反映真实编织结构和编织纱线截面形状的三维热阻网络传热模型。
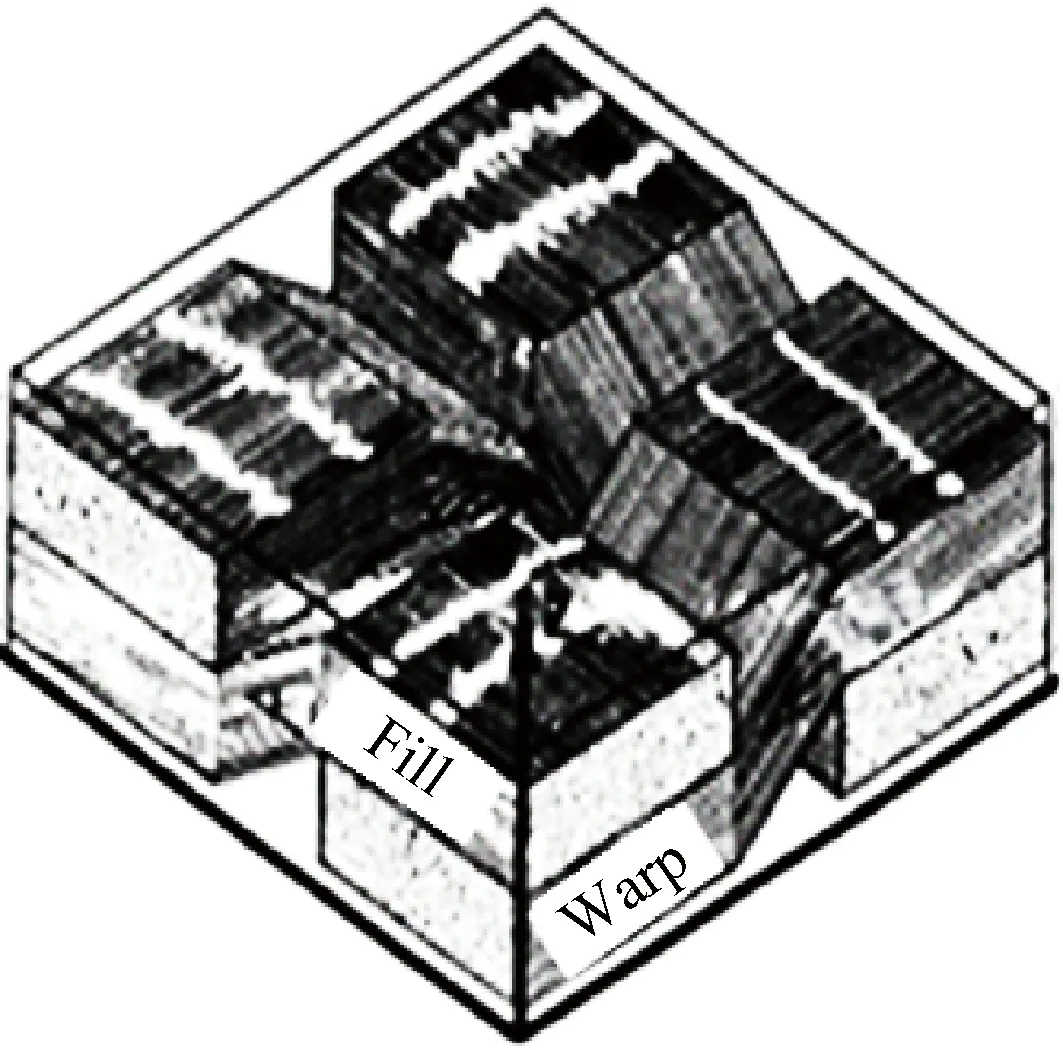
图7 Ning和Chou建立的TDWC简化模型[80]
事实上,TDWC中的编织纱往往并非由单一均匀物质构成,而是由更细小的纤维和基体复合而成,其结构类似于UFRC。因此对TDWC展开热分析时,建立不同尺度的热分析方法对TDWC等效导热系数的高精度预测有重要意义。
Zhu和Li[82]基于分形法,建立了TDWC的跨尺度等效导热系数分析模型,推导了TDWC的等效导热系数计算公式。该模型由两个不同尺度的子模型组成,分别为具有纤维丝尺度特征的纱线模型和具有纤维编织尺度特征的细观模型,如图8(a)所示。Zhu模型虽然考虑组成纱线的纤维结构特征,但是仍不能很好的反映编织纱线的真实编织结构特征。Yoshihiro等[83]利用热网络法建立了更符合TDWC真实纱线编织结构特征的跨尺度热分析数学模型(见图8(b)),并推导了TDWC的等效导热系数计算公式。
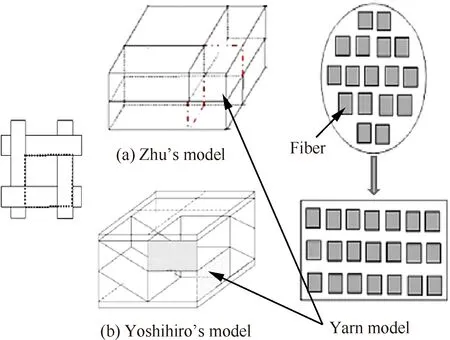
图8 Zhu[82]和Yoshihiro[83]建立的跨尺度TDWC模型
以上建立的工程数学计算模型有助于TDWC等效导热系数的快速工程预估,但是工程数学计算模型不能很好地反映TDWC真实微观结构特征,使得计算值与试验值之间有一定误差。为解决这一问题,相关学者们结合TDWC的真实微观结构特征建立了多种数值仿真模型,用于计算TDWC的等效导热系数。
Siddiqui和Sun[84]利用扫描电子显微镜对TDWC的重复单元进行分析,并建立了一种适用于TDWC等效导热系数预测的RVE模型。尽管该模型能够体现编织纱线宏观的编织结构特征,但模型中纱线和基体均为均质材料,仍不能充分反映复合材料的微观结构特征。Vorel和Michal[85]基于Mori-Tanaka平均方案的两步均匀化过程,建立了包含纤维水平(微观尺度)、纱线水平(细观尺度)和层压体水平(宏观尺度)的三尺度均匀化方法。该方法在各尺度上进行解耦运算,运算相对简单,消耗计算资源少,但是该模型中未能考虑材料的孔隙、裂纹以及界面热阻等微观结构特征。
与UFRC材料相似,TDWC因其制造工艺等问题,其内部会存在孔隙和裂纹,这些孔隙和裂纹会对TDWC的传热特性有显著影响,研究表明孔隙和裂纹的存在会使得传热特性降低50%左右,热扩散系数降低8%左右[86]。Farooqi和Sheikh[86]基于Puglia等[87]得到的TDWC微观结构SEM显微照片,采用跨尺度分步均质化的方法,建立了包含孔隙和裂纹的3个不同尺度的子模型,形成了一种通过典型单元来模拟预测TDWC等效导热系数的方法。该模型将编织纤维结构规则化,且根据二维SEM纤维照片将裂纹二维拉伸为3维裂纹,如图9所示。这使得其建立的建模与实际材料微观结构还是较大出入,导致对等效导热系数的预估精度不理想, 等效导热系数预测误差高达11.63%。

图9 考虑TDWC不同特征孔隙的多尺度模型[86]
Liu等[88]同样基于Puglia等[87]得到的TDWC微观结构SEM显微照片,建立了与Farooqi模型不同的跨尺度有限体积数值模型,如图10所示。该模型能够较为准确地反映TDWC中编织纤维的真实编织结构。利用该模型,Liu等[88]着重考虑了纱线和基体的孔隙率对TDWC等效导热系数的影响。
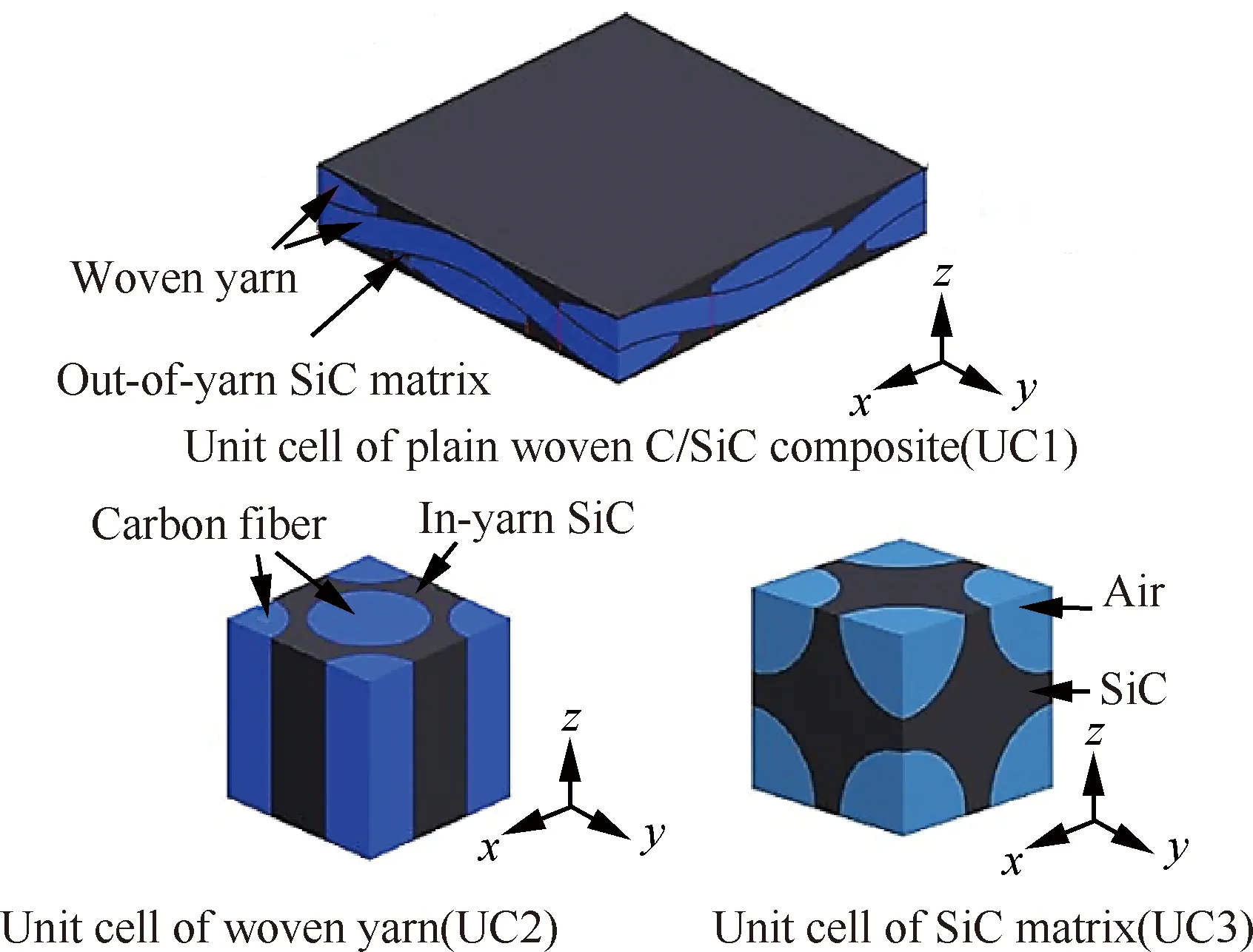
图10 Liu等建立的多尺度TDWC模型[88]
2.5D编织复合材料作为TDWC的一种,学者们也展开了较为系统的研究。Dong等[89]基于材料的微观结构特征建立了2.5D编织复合材料的跨尺度热分析模型,如图11所示。该跨尺度模型包括微观尺度和细观尺度两个子模型,其中微尺度模型包含纤维和孔隙,用于预估编织纱线的等效导热系数;细观尺度模型以微尺度模型得到的纱线等效导热系数为基础,分析2.5D编织复合材料的整体导热行为。研究结果表明,有限元分析结果与试验结果基本一致,误差小于5%。
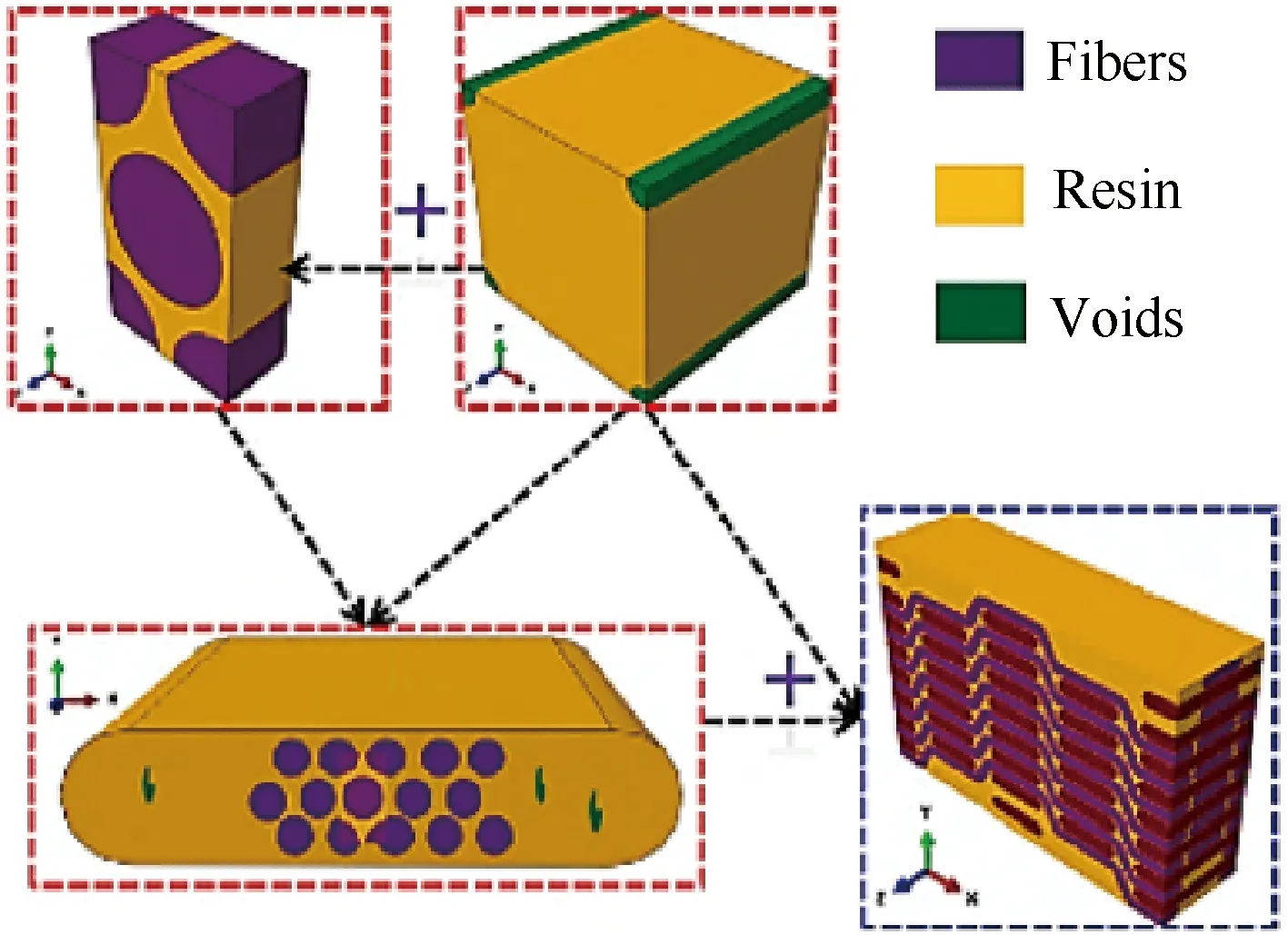
图11 2.5D编织平板多尺度模型[89]
在对TDWC导热系数进行预估时,同样需要考虑界面热阻的影响。Xu等[90]基于Mei[91]得到的C/SiC复合材料微观结构的SEM显微照片,建立了包括纤维尺度(微观尺度)和纱线尺度(细观尺度)的跨尺度分析RVE模型,如图12所示。与Farooqi模型和Dong模型不同,Xu模型在纤维尺度建模中引入了UFRC中纤维与基体间的界面热阻,并在纱线尺度建模中引入了正交纱交点处的大孔隙。
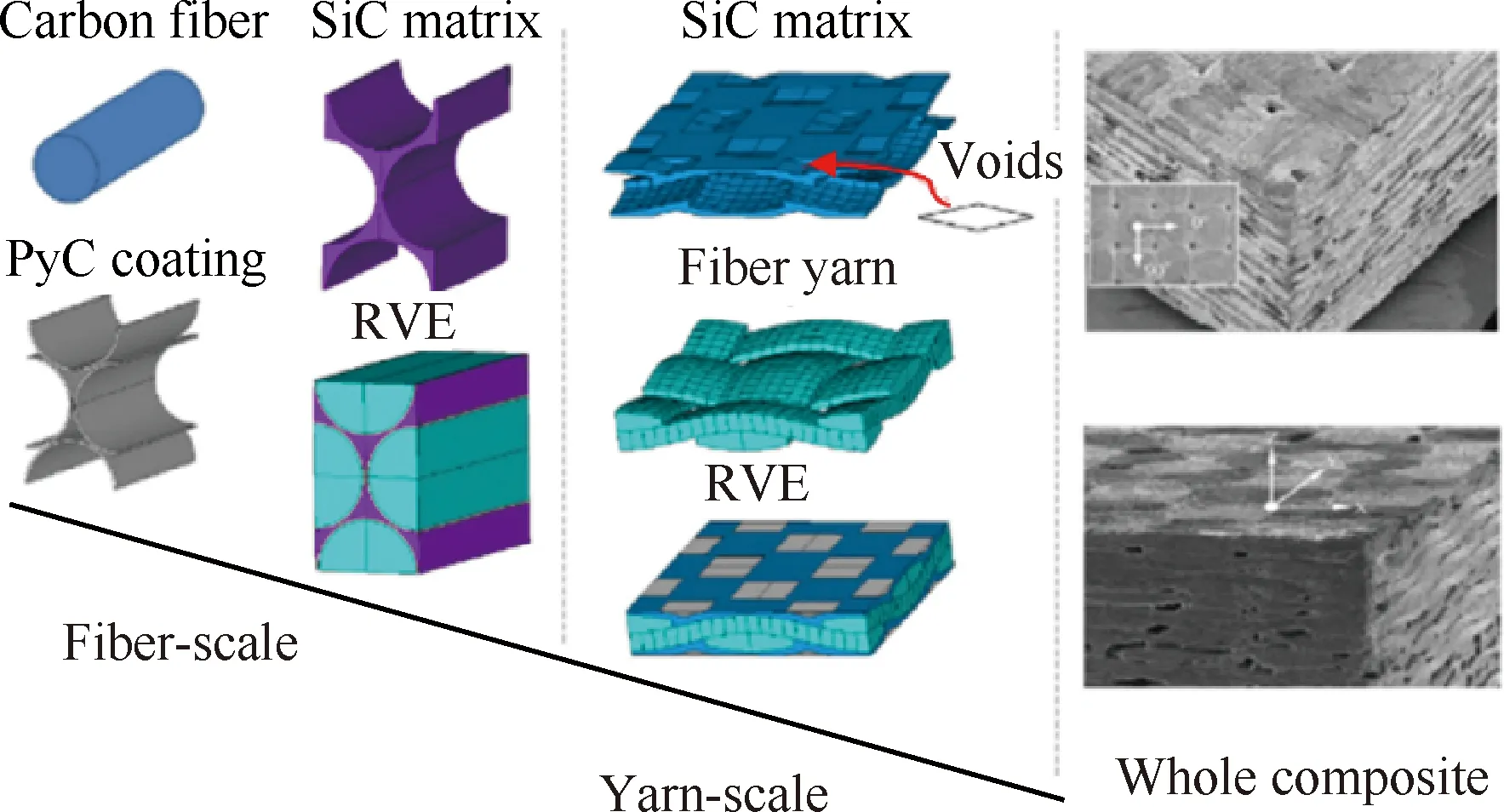
图12 考虑界面相和孔隙的多尺度TDWC模型[90]
上述几位学者都是先得到材料显微照片后再根据不同结构特征建模。这种方式虽然能够反映材料的编织结构、孔隙以及裂纹特征,但是无法还原编织纤维之间的挤压变形,孔隙以及裂纹等结构特征的真实三维特性。Gao等[92]采用X射线计算机断层成像(XCT)技术建立了2.5D陶瓷基复合材料三维RVE模型,如图13所示。该模型根据三维重构技术真实还原了复合材料的编织结构特征和三维孔隙特征。受益于更贴近真实结构的RVE模型,Gao模型对该材料的等效导热系数预估精度很高,与试验值相比材料在3个导热方向上的等效导热系数的误差仅分别为0.87%、0.25%和8.51%。
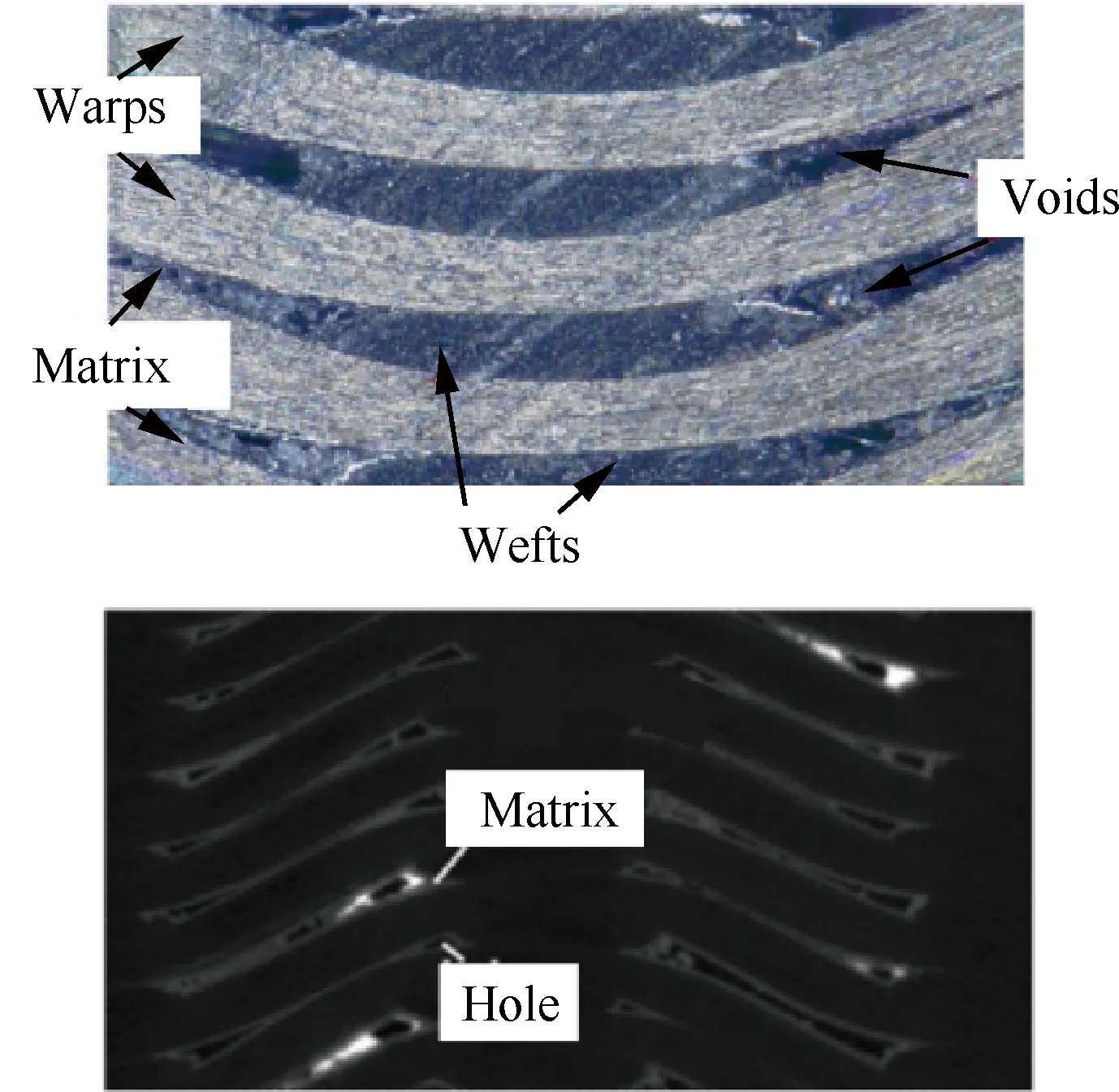
图13 基于XCT三维重构技术的TDWC模型[92]
但是,以上模型都只在材料静态时对材料进行等效导热系数的预估计算,而材料在工作载荷下会发生变形,也会影响到材料的导热系数。Chen等[93]对TDWC沿厚度方向进行温度-位移耦合稳态分析。该分析基于平纹复合材料的细观尺度RVE单元模型,给出了周期性位移边界条件和沿厚度方向的温度梯度,预测了复合材料在单轴应变作用下热导率的退化。
通过各国学者的努力,目前通过材料的电镜照片或X射线计算机断层成像技术,可以建立起反映材料基本微观结构特征的跨尺度RVE模型。在这些模型的基础上采用跨尺度均匀化热分析方法能够较为准确的预测TDWC等效导热系数。
然而目前建立的跨尺度RVE模型,其核心思想仍源自空间上的周期性假设,无法很好体现使用TDWC制成的热端部件的真实壁厚、复杂型面等宏观全尺寸结构特性,因此未来考虑TDWC热端部件宏观结构特征与TDWC自身结构特性的耦合作用,建立TDWC全尺寸跨尺度耦合等效导热系数预测方法将是一个重要的研究方向。
1.3 TDBC 3维纤维编织复合材料
与UDFC、TDWC相比,TDBC编织方式多样,如三维五向编织、三维四向编织以及三维正交编织等不同编织方式。TDBC的编织结构具有很强的三维空间交错性,这使得无法建立TDBC的热阻网络,进而导致无法建立其工程数学计算模型。目前学者主要通过建立TDBC的RVE模型来预测其等效导热系数。
在三维四向编织TDBC导热系数预估方面, Mohajerjasbi[94]建立了“米”字型枝状胞体RVE模型。程伟等[95]在此基础上,用六棱柱代替圆截面或椭圆截面的纤维束,同时考虑了纤维束在相交处重叠体积,建立了一个用于热分析的RVE模型,如图14(a)所示。基于该模型程伟研究了纤维体积分数和纤维编织角对TDBC等效导热系数的影响。
考虑到“米”字型枝状胞体RVE模型与三维四向编织TDBC的真实编织结构存在较大的差异,为了建立更符合真实结构特征RVE模型,杨振宇等[96]以成型后的编织复合材料为研究对象,根据试验的结果,初步建立了一种能够反映TDBC纤维束的交织方式的RVE模型,如图14(b)所示。Liu等[88]在杨振宇模型[96]的基础上,建立了三维四向编织TDBC等效导热系数预测的RVE模型。与程伟等[95]使用的“米”RVE模型相比,Liu模型预估得到的等效导热系数偏差更小。但Liu等建立的RVE模型中编织纱线的截面人为假设为六边形,且编织纱线的偏转存在突变等不足。
Gou等[97]进一步建立了能够基本反映三维四向编织TDBC真实编织结构的RVE热分析模型,如图14(c)所示。Gou等还建立一套模型简化方法和相应的热分析边界条件计算方法。通过该方法可以将全单位计算RVE模型减小为原来的1/2、1/4和1/8,大大节约了计算资源和计算时间。但是该模型未考虑材料的界面热阻、孔隙以及裂纹等微观结构特征,同时也未能反映材料编织时纱线相互挤压变形等编织结构特征,这导致该模型预测等效导热系数的误差达21.6%。
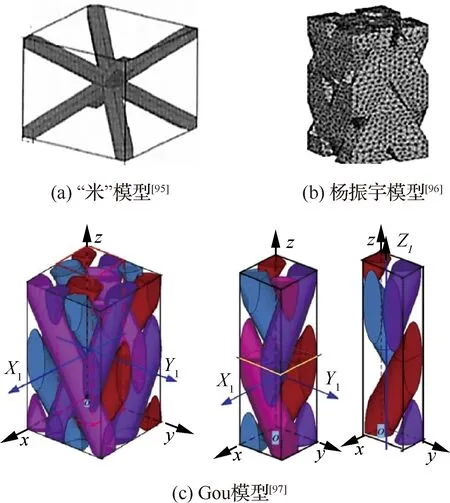
图14 三维四向编织TDBC热分析RVE模型
在三维五向(5D)编织TDBC导热系数预估方面,由于其编织方式复杂,且研究起步晚,目前仅有少部分研究工作。李典森等[98-99]、江华[100]在分析三维五向编织TDBC纱线编织走向的基础上,建立了三维五向编织结构的RVE模型,并基于建立的模型计算了三维五向编织TDBC的等效导热系数,如图15(a)所示。卢子兴等[101]建立了三维全五向(Q-5D)编织TDBC的参数化热分析RVE模型,计算得到了相应的等效导热系数和热膨胀系数,如图15(b)所示。
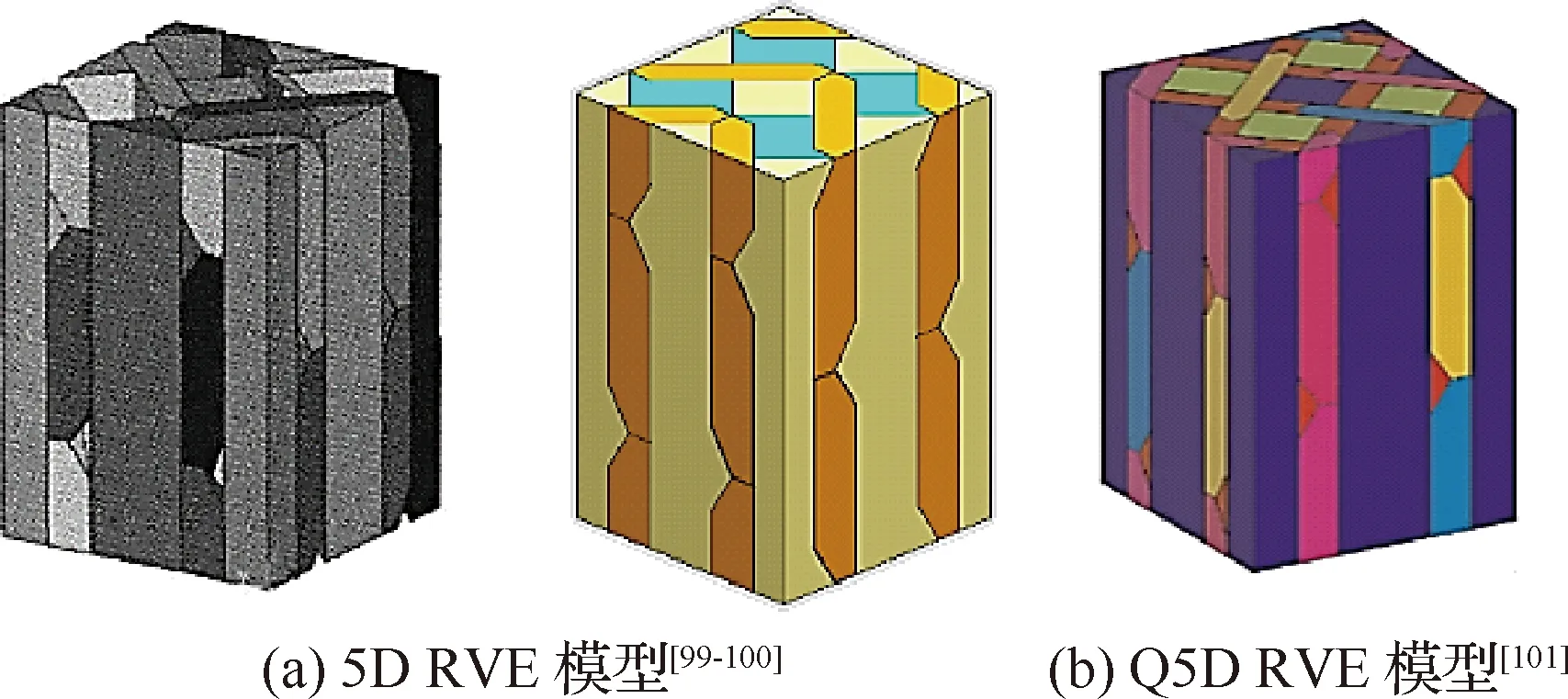
图15 三维四五编织TDBC热分析RVE模型
除了三维五向编织和三维四向编织以外, Lee等[102]还针对四轴多向正交编织复合材料 (four-axial multiaxial Non-Woven Composites,NWC),在假设纤维具有横向各向同性、基体具有各向同性、忽略了增强材料与基体之间的界面热阻的条件下建立热分析RVE模型,并利用张量坐标变换法对NWC的等效导热系数进行了预测,如图16(a)所示。Jiang等[103]基于螺旋几何RVE模型,对三维螺旋编织TDBC的等效导热系数进行了预测,如图16(b)所示。
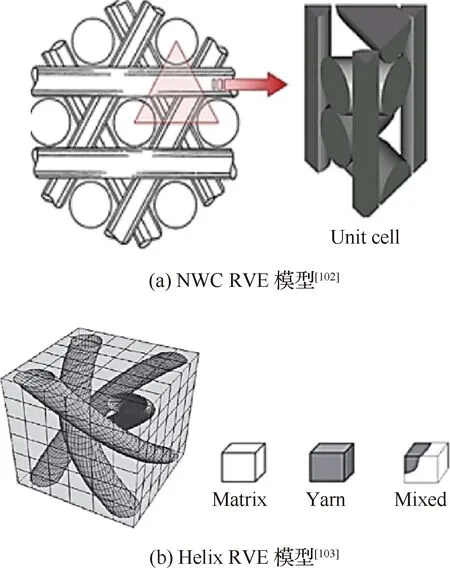
图16 NWC RVE模型和Helix RVE模型
以上针对不同编织方式建立的TDBC单一尺度热分析RVE模型,虽然能够对TDBC进行等效导热系数的预估,但是模型都是建立在特定尺度以及均匀化理论的基础上,故此无法考虑纱线中纤维等结构特征带来的影响,导致预测值与试验值有较大的误差。近年来已经有学者开始构建针对 TDBC热分析的跨尺度模型。
Dong等[104]建立了包含纤维丝微观尺度、纤维束细观尺度以及构件宏观尺度的跨尺度热分析模型,如图17所示。该模型包括反映纤维丝结构特征的微观尺度RVE模型、反映纤维束编织结构特征的细观尺度 RVE模型以及反映构件整体特性的宏观尺度模型。基于前两者对TDBC的等效导热系数进行预估,利用构件宏观尺度模型揭示了TDBC的导热结构效应。
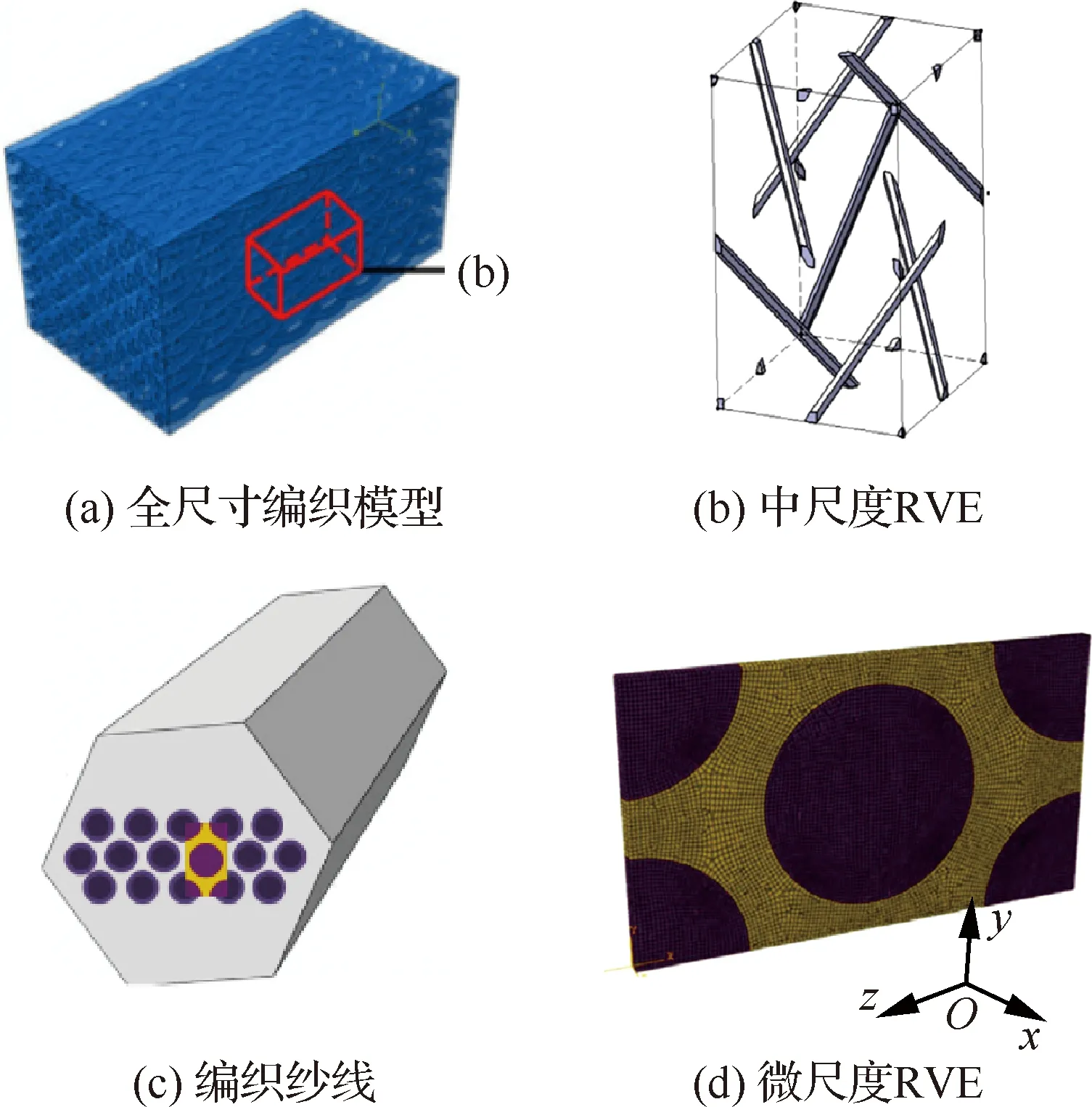
图17 Dong等建立以的多尺度TDBC模型[104]
Fang等[105]针对三维四向编织TDBC,建立了纤维丝微观尺度和纤维束细观尺度的跨尺度分析模型。同时采用非对角碰撞矩阵的多弛豫时间晶格玻尔兹曼模型,结合半晶格划分方法对TDBC的有效导热系数进行了预测。与前文Gou模型相比,Fang模型能够反映三维四向编织TDBC纤维丝微观尺度和纤维束细观尺度两个尺度下的结构特性,等效导热系数预估精度显著提高,误差为9.89%。
跨尺度分析方法可以分析不同尺度结构特征对TDBC等效导热系数的影响。但以上跨尺度分析模型,都是人为简化后构建的规则几何模型,这种建模方式无法充分体现材料的多孔性、编织纤维空间分布的重叠性、随机性等真实结构特性。为解决这一问题,近年来有研究人员开始利用CT技术对材料进行三维重构,来建立相应的热分析模型。
Huang等[106]基于三维重构技术建立了具有不同孔隙率的多孔金属纤维烧结板(Porousmetal Fiber Sintered Sheet,PMFSS)微观结构随机纤维几何模型,如图18所示。Huang模型比Fang模型,更能准确体现纤维编织型材料的真实微观结构特征,因此利用Huang模型来预测材料的等效导热系数比Fang模型更为准确(孔隙率不超过20% 时Huang模型预测误差小于5%)。
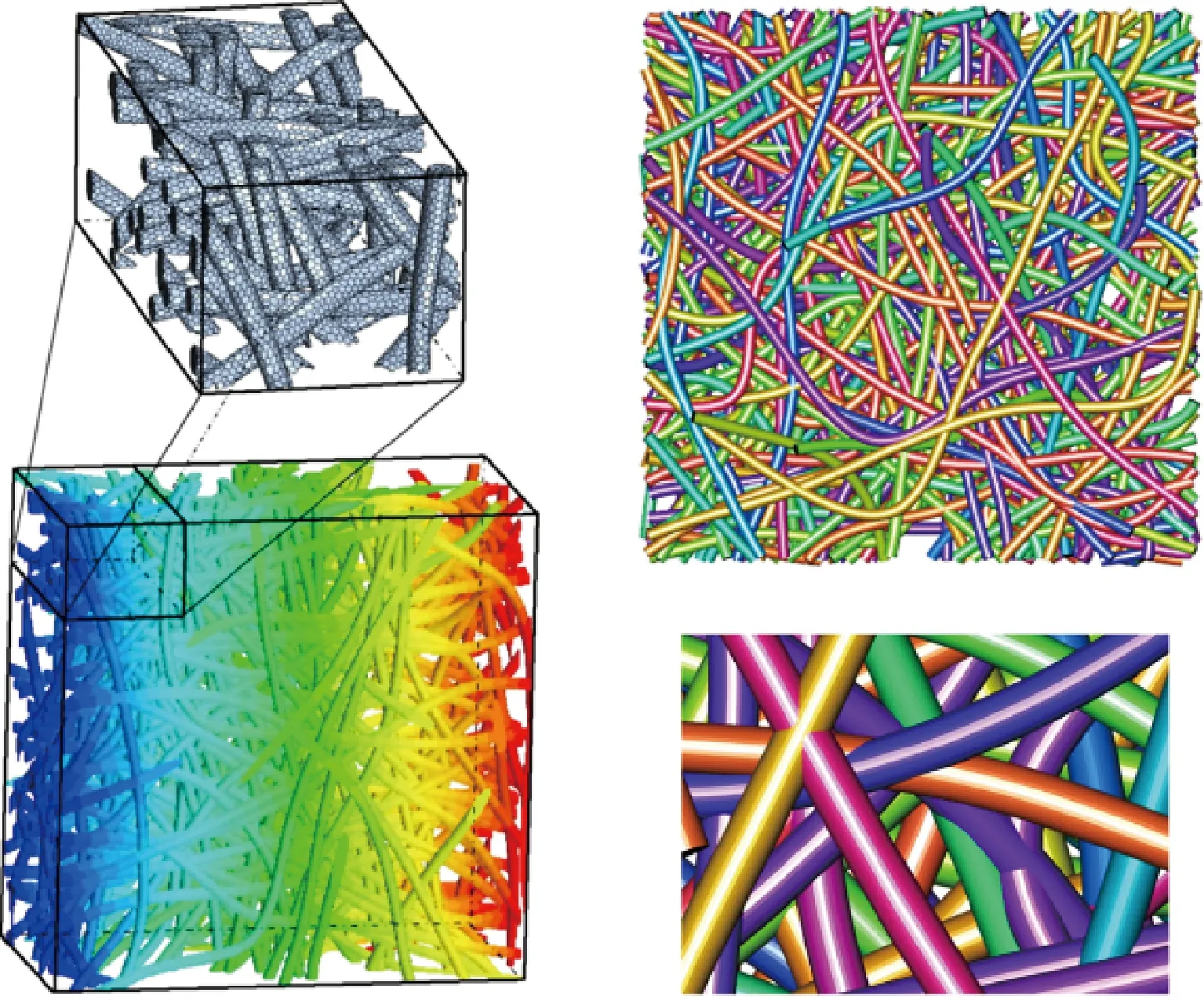
图18 基于XCT三维重构技术的TDBC模型[106]
综合来看,TDBC结构复杂、建模难度大,且TDBC的热分析起步晚,未来以三维重构技术为支撑,建立反映TDBC真实微观结构特性的计算模型将是一个主要的发展趋势。但需要注意的是,利用三维重构技术得到的计算模型会包含大量跨尺度的结构信息,如何针对这些信息,建立精细化、计算资源可承受的跨尺度分析方法和跨尺度耦合计算方法将是未来TDBC等效导热系数预估的一个很重要的研究方向。
2 CMC热端部件的热分析方法
目前针对CMC热端部件,常采用试验测试和数值仿真等手段对其进行热分析。同时由于在高温环境下CMC材料会发生氧化,因此在实际工程应用中,依然需要采用冷却技术对其进行热防护,目前已有部分学者针对CMC热端部件的冷却结构开展了设计分析。此外,包括增材制造技术在内的先进复合材料制造技术,对现有CMC热端部件的热分析方法也提出了新的挑战。针对上述四方面的内容,本节首先总结分析了CMC热端部件的试验和数值仿真热分析方法现状,然后介绍了CMC热端部件冷却结构的设计及热分析现状,最后初步探究了以增材制造技术为代表的先进制造技术对CMC热端部件热分析方法可能带来的影响。
2.1 CMC热端部件试验测试
试验测试是目前开展CMC热端部件热分析的重要手段之一。目前已有多个发动机制造商和研究团队对CMC热端部件开展了多项热态试验分析。
CMC燃烧室作为典型的CMC热端部件之一,目前研究人员已经对其进行了多次热端验证试验[107-113]。Bhatia等[107]对全环形CMC燃烧室(见图19(a))在实际发动机的慢车转速(40 000 r/min)和全功率转速(57 000 r/min)之间进行了250次循环,在整个试验过程中,CMC燃烧室在燃气环境下都没有出现烧蚀等问题。Hald等[108]在典型燃烧工况下,对采用CMC材料的新概念火箭发动机燃烧室(见图19(b))进行了试验研究。研究发现,得利于CMC材料的应用,该燃烧室的热循环敏感性降低,但由于CMC材料的导热系数较低,使得该燃烧室的局部温度梯度高达1 000 ℃/mm。此外Lebel等[109]对火箭发动机CMC燃烧室壁板进行了试验研究,重点关注了CMC燃烧室壁板在燃烧环境下的热应力问题。以上研究通过对CMC燃烧室开展试验测试,验证了其在发动机高温环境下的可靠性,为CMC燃烧室设计提供了重要数据支撑。

图19 CMC燃烧室
CMC涡轮叶片作为另一个重要的CMC热端部件,一直是航空发动机制造厂商的重点研究对象。例如,Verrilli等[6]在1 200 ℃的高温气流下,对使用SiC/SiC材料的整体编织CMC涡轮叶片进行了高温台架试验,试验发现在高温气流下连续工作50 h,CMC叶片没有发生明显退化,而合金叶片损坏严重,如图20(b)和图20(c)所示。试验验证了CMC涡轮叶片在高温环境下工作的结构可靠性,同时试验过程中使用光学高温计测量了CMC涡轮叶片表面温度,为CMC涡轮叶片的热分析提供了宝贵的试验数据。

图20 CMC涡轮叶片[6]
除了上述对CMC材料发动机整体热端部件进行的试验研究,还有许多学者对CMC构件进行了高温试验测试。
Bouquet等[114]开发和测试了一种全热结构C/SiC换热器,并在超燃冲压发动机试验台上进行了13次短时间试验(每次试验燃烧过程存在5 s), 测试时其换热热流密度高达1.5 MW/m2,且测试完成后换热器结构没有出现高温结构损伤。Peng等[115]针对采用主动冷却技术的CMC复合平板进行温度场测试,试验时CMC平板的最大表面温度达2 000~3 000 K,结果表明采取主动冷却技术的C/SiC复合材料层板结构,仅使用较少冷却量即可为高超声速吸气推进系统在高温工况下提供有效热防护。Reimer等[116]在高超声速条件下,对C/C-SiC圆管构件进行了发散冷却试验研究,该研究验证了发散冷却在CMC圆筒构件上的热防护性能,同时还对高热负荷条件下C/C-SiC材料的氧化和侵蚀问题进行了探究,如图21(a)所示。
Michael等[117]在燃气环境下对一类氧化物CMC材料的高温耐久性进行试验研究,探究了在1 150 ℃、240 m/s高温高速气流的周期性冲刷下试验样品的损伤演化机理,同时分别用单波长高温计和热电偶监测前后表面温度。如图21(b)所示。刘宁夫等[118]研制了超高温冷热冲击试验装置对氧化锆陶瓷试件瞬态抗冷热冲击性能进行了试验研究,验证了超高温冷热冲击试验装置的可信性和有效性,为其在冷热冲击试验中的工程应用提供了设计依据。

图21 CMC部件试验
上述研究为验证CMC热端部件在高温工作环境下的结构可靠性及热防护措施的有效性提供了非常重要的支撑数据。但是由于CMC热端部件的试验件制造工艺复杂且价格昂贵,导致试验成本高昂。另一方面,受制于目前试验测试手段,试验方法难以获取CMC热端部件内部热量的传输机制,不利于CMC热端部件的正向热设计。因此在试验测试之外,亟待建立考虑CMC热端部件结构特征的热分析仿真方法。
2.2 CMC热端部件热分析仿真方法
目前针对CMC热端部件的温度场计算,主要有3种方法。第1种方法是不考虑CMC材料导热各向异性的整体均匀化计算方法,该方法在计算时将CMC材料看作均质材料,在热分析时直接用CMC材料的各向同性等效热物性进行计算,这种方法与传统金属材料热分析方法类似。第2种是考虑CMC材料导热各向异性的整体均匀化计算方法,该方法基于纤维(编织纱)的走向,依据试验测试或根据第2节介绍的CMC等效导热系数数值计算结果,获得材料3个方向的宏观等效导热系数,再将其赋给宏观尺度下的部件热分析模型,进而完成温度场的计算。第3种方法是细观尺度计算方法,该方法考虑增韧纤维束的真实编织结构,根据编织纱线的编织走向和基体材料特性赋值各向异性的导热系数,针对部件开展全尺寸(Full Size)建模,并利用有限元模拟等方法进行数值仿真分析。
2.2.1 不考虑CMC材料导热各向异性的整体均匀化计算方法
该方法将计算模型简化为均质模型,计算时将CMC材料的宏观等效热物性参数设置为各向同性,完成温度场的计算。
Murthy等[8]利用该方法结合计算流体力学分析获得了CMC叶片上的温度分布,并为CMC叶片失效概率的仿真研究提供了热边界条件。Wang等[119]对用于综合热防护系统的多层陶瓷基复合蜂窝夹层板进行数值仿真研究。研究根据层板的几何结构,推导了其沿厚度方向的有效导热系数以及热扩散系数,如图22所示。计算时未考虑CMC材料导热各向异性,其数值仿真结果与试验结果[120]的相对误差约为10%。

图22 多层陶瓷基复合蜂窝夹层板[119]
2.2.2 考虑CMC材料导热各向异性的整体均匀化计算方法
考虑CMC材料导热各向异性的整体均匀化计算方法在计算时,忽略CMC材料增韧纤维的编织结构等特征,将计算模型简化为均质模型;通过设置3个方向上的导热系数来表征CMC材料的导热各向异性。具体计算中,该方法包括不考虑部件型面对各向异性方向的影响以及考虑部件型面的影响两种方法。
当不考虑涡轮叶片等热端部件的型面对各向异性方向性的影响时,计算中直接设置全局坐标系下3个不同坐标方向上的宏观等效导热系数,完成温度场的计算,如图23所示。
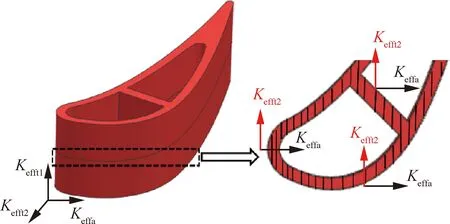
图23 全局坐标系下各向异性等效导热系数示意图
赵宏丽[121]和陈龙淼[122]分别采用这种方法对碳/碳编织复合材料的火箭发动机尾喷管和复合材料炮管温度场进行数值仿真研究。Nita等[123]针对CMC涡轮叶片开展了试验和数值模拟研究,首先针对叶片进行了高温燃气叶栅试验,并用红外热像仪测量了叶片壁面的温度,然后在数值模拟中,将试验结果作为边界条件,并利用该方法设定CMC材料的各向异性物性参数,对该CMC涡轮叶片的热应力进行了详细分析。徐瑞[39]针对Mark II型涡轮叶片,研究了导热系数的各向异性以及分散性对涡轮叶片温度场分布的影响研究中同样采用该方法,即给定了涡轮叶片3个方向的宏观等效导热系数,获得了叶片高温区域随导热系数变化的规律。
上述关于CMC热端部件的热分析研究中,都是直接全局给定3个方向的导热系数,没有考虑叶片等热端部件的复杂型面与CMC材料导热系数各向异性耦合作用的影响。但是气冷CMC涡轮叶片等热端部件的表面曲率在空间上变化剧烈,导热系数的主方向和全局计算坐标系之间的夹角在空间上存在一定的分布规律。因此,基于全局计算坐标系,直接设定3个坐标方向导热系数为定值的假设,将会导致明显的误差。
考虑部件型面对各向异性方向的影响时,计算中就需要考虑CMC材料3个方向的导热系数随热端部件型面变化的空间分布特征。屠泽灿等[124-125]根据材料编织方向及CMC涡轮叶片型面来赋值3个方向的等效导热系数,即导热主方向坐标系(ζ,η,v)中的ζ方向为材料编织方向,该方向始终平行于叶片型面,即叶片型面切线方向,如图24中的Keffa。η方向为材料编织厚度,该方向始终垂直于叶片型面,即叶片型面厚度方向,如图24中的Kefft2。v方向的等效导热系数为叶片高度方向的导热系数,如图24中的Kefft1。

图24 考虑型面特征下等效导热系数示意图
Liu等[126]同样通过该方法对二维编织SiC/SiC-CMC涡轮导向叶片进行了热力学数值仿真研究。Shen等[127]在试验研究的基础上,对CMC涡轮导向叶片在热载荷作用下的应力应变进行了数值计算。计算时引入材料映射模型,通过修改有限元计算模型的局部坐标系来考虑部件型面对各向异性物性参数方向的影响,其计算坐标如图25所示。
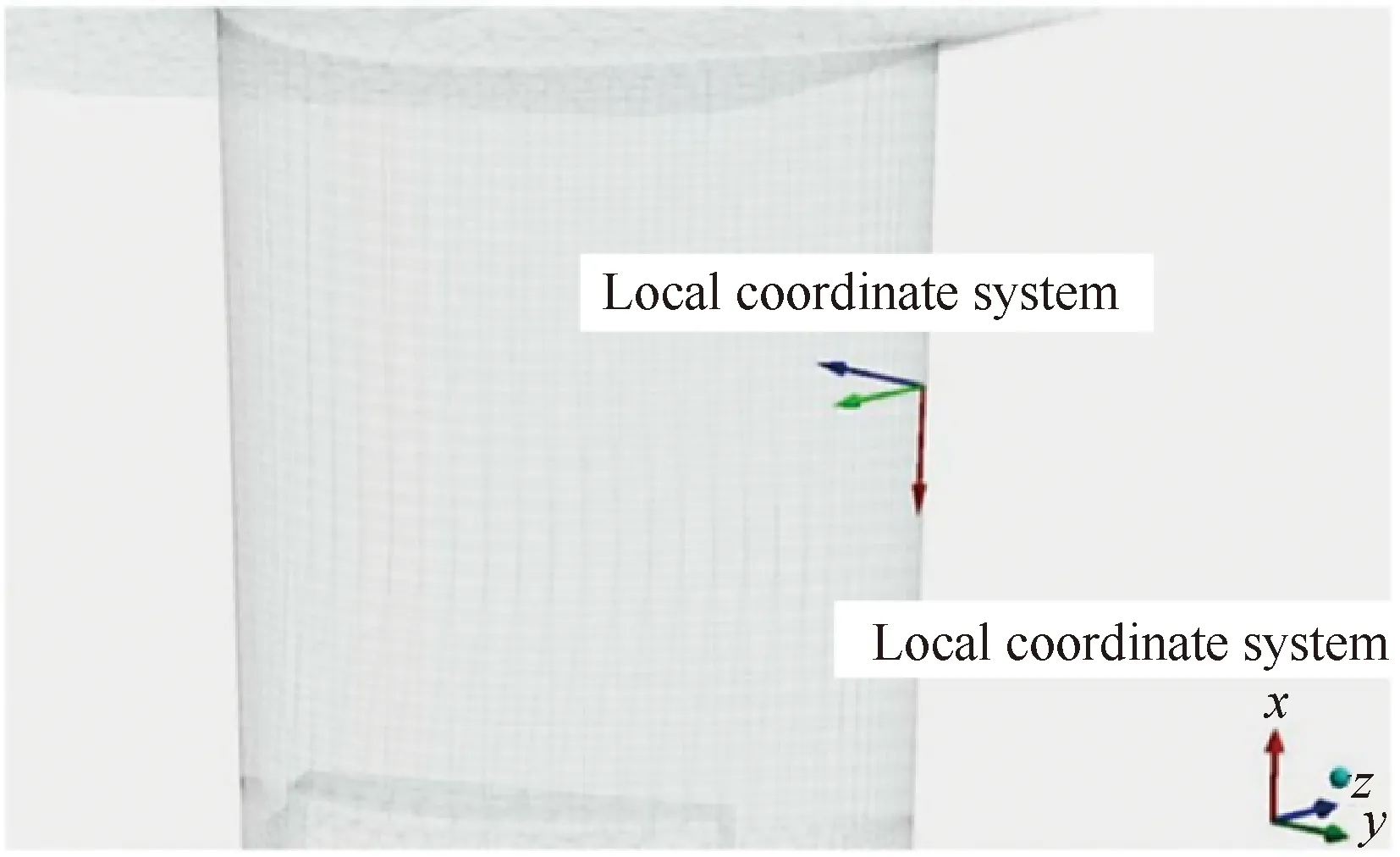
图25 计算坐标示意图[127]
在随后的研究中,Tu等[128]发现在涡轮叶片等存在薄壁结构的热端部件热分析中,尽管考虑了宏观构件型面扭曲的影响,基于RVE模型预测的ETC与试验值相比仍有15.62%的误差。为克服这一问题,屠泽灿[124]考虑涡轮叶片的真实壁厚以及三维五向编织结构的整体性,建立了全尺寸跨尺度计算模型预测真实壁厚下CMC材料的ETC,并将预测值结合2.2.2节所述方法对CMC涡轮叶片进行热分析。计算结果表明直接使用整体均匀化的计算方法得到的结果有明显误差,如在x/l=0的叶片前缘点,计算结果和试验结果的相对误差达到了103%,且模拟得到的该区域综合冷却效率分布规律与试验结果也差异较大。使用该计算方法得到的结果精度得到明显提升,在特征区域S1(叶片前缘)、S2(部分压力面)和S3(部分吸力面)计算和试验结果的相对误差分别为8.48%、7.75%和2.11%。
2.2.3 细观尺度计算方法
增韧纤维作为CMC材料一个不可忽视的结构特征,对CMC热端部件温度场分布和热量传输方式有显著影响,CMC材料导热各向异性的特性也取决于增韧纤维取向[129]。3.2节中的整体均匀化的计算方法忽略了这一具有显著影响的结构特征,无法对CMC热端部件进行高精度的热分析,而基于细观尺度编织结构的全尺寸建模方法则弥补了这一缺陷。
该方法考虑增韧纤维的真实编织结构,从纤维束等细观尺度引入等效导热系数,然后根据编织纱线的编织走向和基体材料特性分别赋值各向异性的导热系数进行CMC热端部件热分析。赵晓[130]针对2.5D编织平板建立包含纱线尺度以及构件尺度的全尺寸分析模型并进行试验验证。从图26试验结果与仿真结果对比可以看出,采用整体均匀化的计算方法无法获得CMC由于纤维编织结构引起波动的温度信息。而全尺寸建模方法能够较为准确的还原CMC的温度场,掌握CMC热端部件内部热量传输机理,有助于建立CMC热端部件精细化热分析方法,进而为CMC热端部件的工程设计提供支撑。
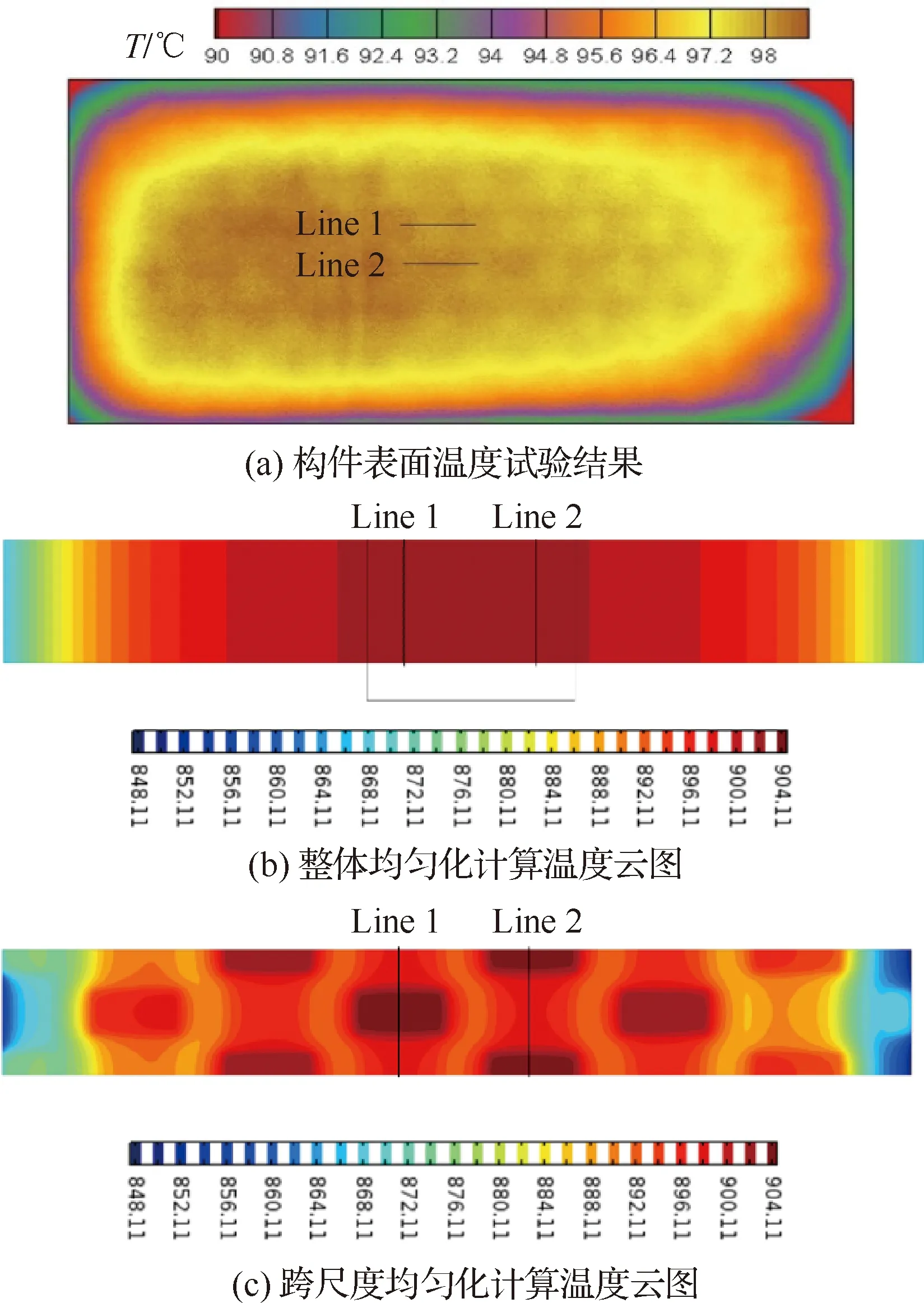
图26 2.5D编织平板数值仿真与试验结果[130]
2.3 CMC热端部件冷却结构设计及分析
当CMC热端部件应用于高温燃气环境中时将面临着严峻的挑战。Smialek等[131]研究CMC材料在高温燃气下的氧化特性以及氧化过程。研究表明,当燃气温度为1 450 ℃时,CMC材料中的SiC基体重量在工作100 h后,每平方厘米上减少了0.18 mg左右,如图27所示。因此当CMC热端部件在高温环境下工作时,有必要对其采取有效的热防护措施。目前已有部分学者基于2.2节介绍的CMC热端部件热分析仿真方法,对CMC热端部件的冷却结构开展了设计分析。
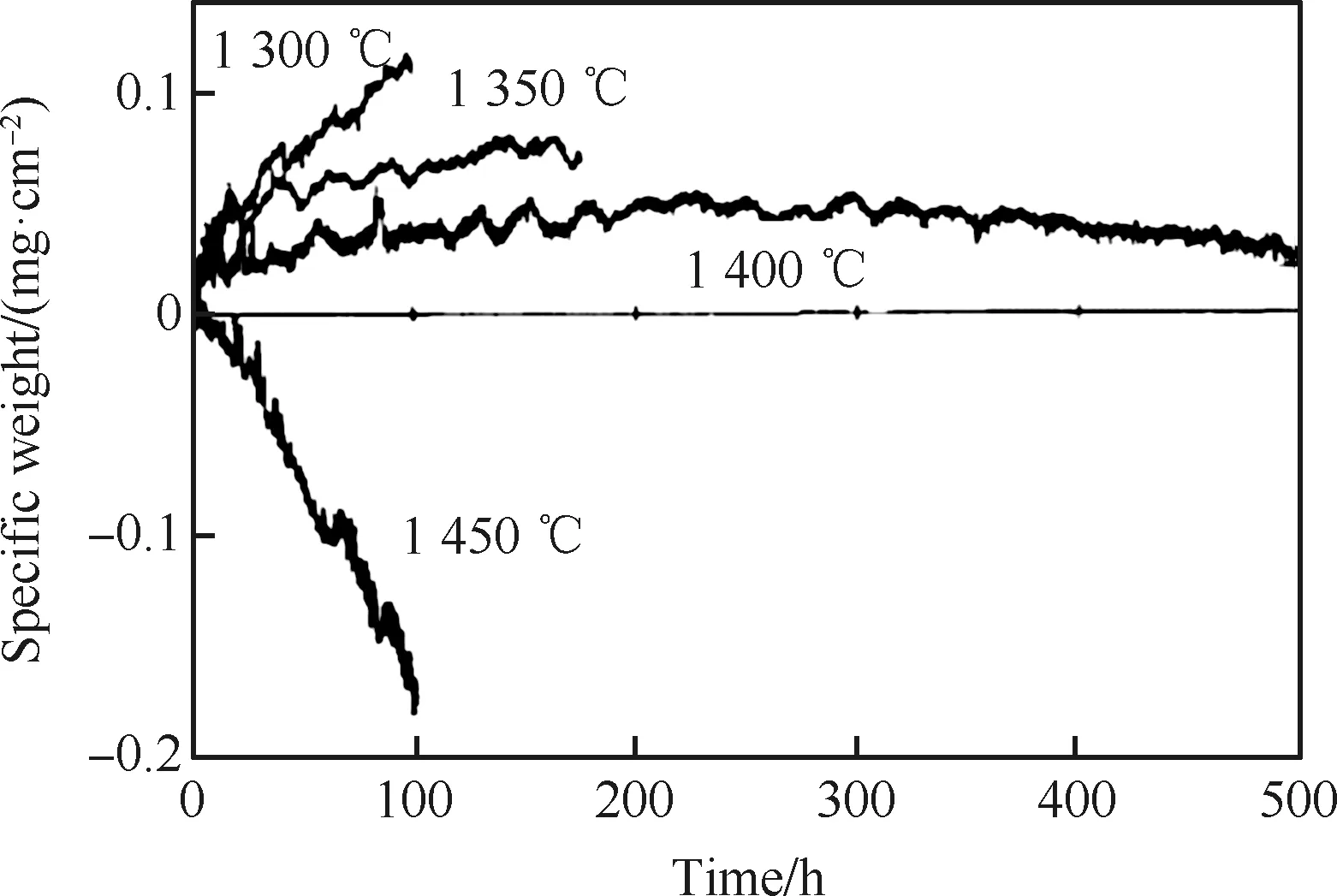
图27 SiC重量变化随时间及温度变化图[131]
强迫对流冷却是一种常用的冷却措施。目前该冷却方式常用于高超音速飞行器、再入飞行器等航空航天器的前缘、机翼等需要热防护的部件中。Ferrari等[132]对采用陶瓷基复合材料的周期性多孔夹层结构进行主动冷却数值仿真研究。获取了不同进气条件下的冷却效果,但计算时基于3.1节介绍的热物性设置方法,未能考虑CMC材料的导热各向异性对冷却性能的影响,如图28所示。

图28 CMC多孔夹层构件及数值仿真云图[132]
考虑到CMC材料的低导热特性及加工工艺,气膜冷却是一种另一种可行性较高并具有较好冷却效果的冷却手段。气膜冷却技术的使用,需在构件上制造出功能各异的离散气膜孔。气膜冷却特性会对CMC热端部件的温度场分布有显著影响。同时与传统均质金属材料不同,CMC材料由于其各向异性的导热特性以及增韧纤维的影响,会使得材料内部的温度场呈现非均匀特征,将导致热量传输特性发生改变,而这反过来又会影响气膜冷却特性[133]。以上CMC构件各向异性导热特性与气膜的耦合作用,导致CMC构件冷却结构的热分析成为一个复杂的耦合分析过程。
为研究CMC热端部件的气膜冷却特性,目前不少学者以简单的CMC平板构件为对象来开展研究。屠泽灿等[134]研究了不同增韧纤维方向对单向纤维增韧CMC平板圆孔气膜冷却特性的影响,其试验研究表明导热各向异性会影响气膜冷却平板内部的热量传输过程,沿纤维增韧方向,热量传输能力得到加强,进而会对气膜覆盖壁面的综合冷却效率及温度分布均匀性产生影响。侯亚东等[135]采用试验研究的方法,研究了不同编织方式(1D/2D/2.5D/3D编织)成型的复合材料平板圆孔气膜冷却特性。其研究表明,不同编织方式对平板内部温度分布有显著影响。Zhong和Brown[136-137]对双层壁CMC平板进行了冲击/气膜冷却特性试验以及数值仿真方法的研究。
上述针对CMC平板气膜冷却的数值仿真研究大都采用基于等效导热系数的整体均匀化模拟方法,即在计算时直接给定CMC平板3个方向的宏观等效导热系数以表征材料导热各向异性,因此,计算得到的是一个均匀化的温度场,无法充分反映材料内部微观编织结构对固体域的内部热量传输过程的影响,进而无法获取材料编织结构对气膜综合冷却效果的影响。
为解决上述问题,近年来已经有研究人员从纤维束编织结构的尺度,即介于纤维丝微观尺度和平板构件宏观尺度之间的细观尺度,建立气膜冷却结构模型并开展热分析。赵晓[130]基于全尺寸编织结构模型研究了2.5D编织结构CMC材料的平板气膜冷却特性及内部温度场分布特征,并对比分析了其与均匀化方法计算结果的差异,如图29所示。其研究结果表明,建立全尺寸编织结构平板模型,从纤维束尺度引入复合材料各个组分等效导热系数的数值计算方法是可靠的。在气膜孔下游约2D范围内计算值与试验值几乎完全吻合,在气膜孔出口至气膜孔下游约6D的区域内,计算结果与试验结果的相对误差在10%以内。而基于均匀化方法获取的冷却效率及平板内部温度场,其与基于全尺寸编织结构方法的结果相比,无论在数值还是分布规律上均有较大差异。
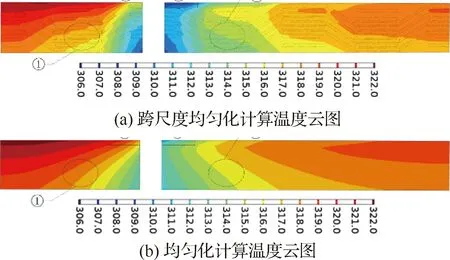
图29 2.5D编织平板数值计算温度场[130]
采用全尺寸编织结构模型可以计算得到CMC构件内部复杂温度场的详细信息,有助于掌握CMC构件内部热量传输机理,进而为CMC热端部件的气冷结构与材料的编织结构开展协同设计提供支撑,以达到高效冷却和低壁温梯度的工程设计目标。
此外,CMC材料自身的多孔性,为发汗冷却的应用提供了先天条件。目前已有学者在CMC平板上对发散冷却进行了试验和数值仿真研究。Dahmen等[138]基于多孔陶瓷基复合材料(CMC)平板,采用试验和数值仿真的方法研究了采取发汗冷却时,不同冷却气体流量对边界层温度、速度和局部表面摩擦带来的影响。Koenig等[139]同样基于多孔陶瓷基复合材料平板,研究了采用发汗冷却时,非均匀冷气流量对CMC平板温度场分布的影响。研究表明CMC材料不同铺层方式对冷却效果有很大影响,如图30所示。上述研究在数值仿真时都未考虑CMC材料导热各向异性带来的影响。但实际上,由铺层方向改变引起的发汗冷却效果变化,除了不同铺层方向改变了流场分布外,不同铺层方向下CMC材料导热主方向发生改变是另一个重要原因。因此需要进一步结合CMC材料的各向异性导热特性探究发汗冷却在 CMC热端部件中的实施效果。
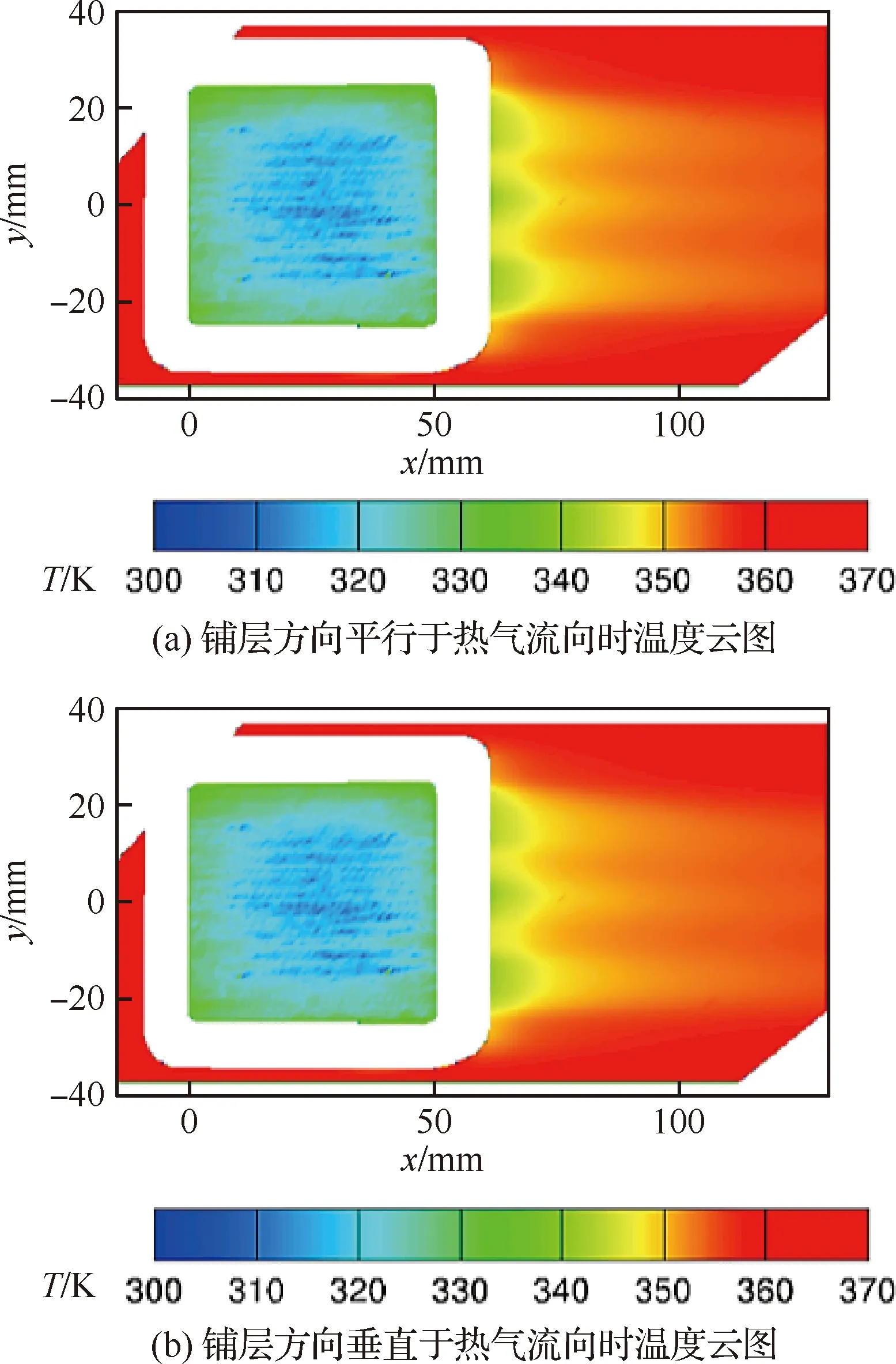
图30 CMC平板发汗冷却构件及温度云图[139]
2.4 先进增材制造技术对CMC热端部件冷却设计的影响
在CMC热端部件的实际工程应用中,将CMC材料内部细观结构与宏观结构进行协同设计以获得高效的热负荷管理是一个重要的研究方向。例如,借助于CMC材料的导热各向异性,工程人员能够将热量高效定向的从热端导向冷端。
目前已有研究学者开始从事这一方面的研究。Cao等[140]将C/SiC平板沿厚度方向开孔,然后在孔中多次填充碳纳米管(CNTs),将圆孔处形成的CNTs/SiC微米柱作为热量传输通道以提高C/SiC复合材料沿厚度方向的整体导热效率,如图31所示。Zhou等[141]通过“纤维微观结构-气孔结构-表面超材料结构”三者协同设计提高复合材料在不同频率的协同吸波性能。
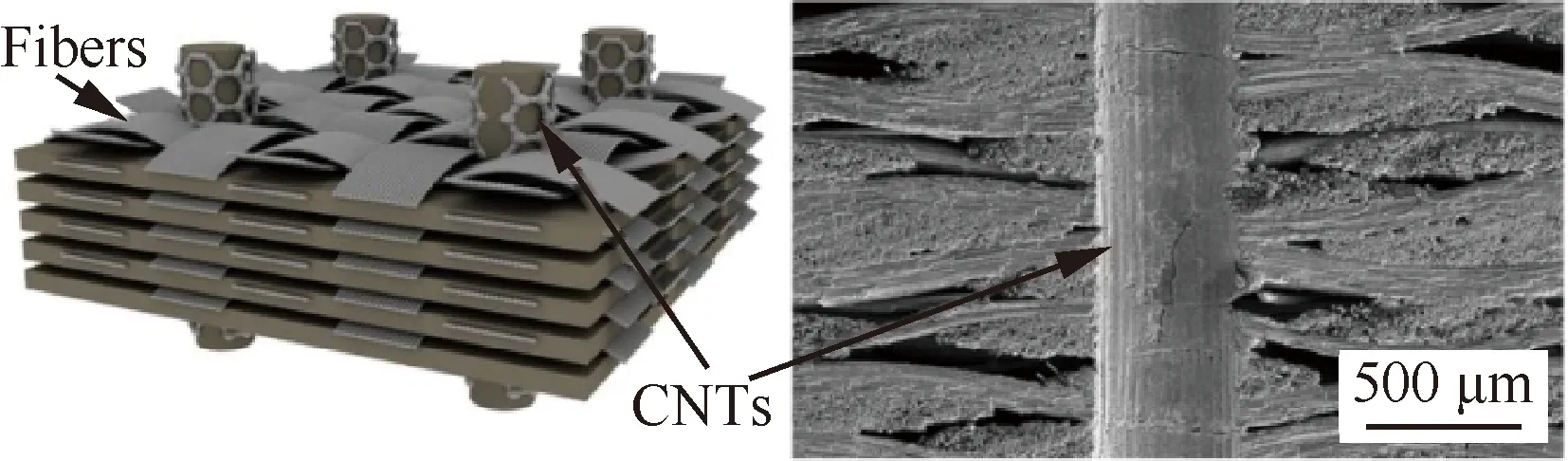
图31 带有CNTs通道的C/SiC复合材料[140]
上述“微观-宏观”协同设计,是未来高性能CMC材料设计的一个重要研究方向。而精细化的CMC材料微观结构设计对材料制造工艺提出了很高的要求,以3D打印技术为代表的先进增材制造技术为其提供了全新的解决思路[142-144]。Mei等[143]通过在微观结构层面精细化设计蜂窝结构,优化材料的吸波性能,同时利用陶瓷3D打印结合化学气相沉积法制备了该具有特定结构的多孔Al2O3/SiC陶瓷基复合材料,如图32(a)所示。杨金山等[144]利用化学气相渗透工艺将SiC基体引入3D打印三维石墨烯,获得三维石墨烯/SiC 复合材料,如图32(b)所示。

图32 3D打印CMC材料微观结构
此外,从图33可知,CMC材料微观结构的尺度在微米量级,而CMC材料热端部件的尺度多在厘米量级,这就对现有热分析方法提出了新的挑战。要在对CMC热端部件进行热分析时,兼顾宏观和微观两个尺度的影响,就需要构件精细化的多尺度计算模型及热分析方法。
基于计算机断层扫描(XCT)的三维重构技术为构建精细化的多尺度计算模型提供了技术支撑。Abdi等[145]和Presby等[146]先后基于计算断层扫描图像对SiC/SiC陶瓷基复合材料的异物损伤进行了数值仿真研究。Chen等[147]基于三维重构技术,建立了研究由裂纹引起的陶瓷基复合材料热机械性能退化全尺寸模型,如图33所示。

图33 基于计算机断层扫描技术的CMC模型[147]
上述多尺度模型包含的几何特征信息极多,当其应用于涡轮叶片等几何尺度较大且结构特征复杂的热端部件时,将会导致计算量激增。所以针对工程实际的热端部件,如何权衡模拟仿真精度和计算资源消耗,建立基于三维微观结构特征重构的热分析模型成为关键。此外,无论是基础材料的宏观热特性参数,还是构件的热响应,都同CMC热端部件的加工工艺和工作载荷等密切相关,且相互之间存在较为突出的非线性耦合关系,因此未来的热分析还需要同制造工艺、力学行为分析等进一步紧密结合,实现多物理场联合仿真。
3 结 论
CMC材料优良的力学及耐热性能,使其在航空发动机热端部件具有较好的应用前景,同时,由于内部非均质的结构特征导致材料的热物性具有明显各向异性及离散性,进而使得传统基于均质金属材料的热分析方法难以适用于CMC材料热端部件。建立CMC材料热物性预测模型和CMC热端部件及其冷却结构的热分析方法,能够为加快CMC材料在航空发动机中工程应用的进程提供有力的技术支撑。
1) 针对CMC材料等效导热系数等热物性参数的预估,目前关于单向长纤维增韧复合材料的导热系数预测方法已较为成熟。而关于2D、2.5D以及3D等内部结构较为复杂的纤维增韧复合材料,目前大多基于扫描电镜等获取的微观结构特征,建立具有明显周期性特征的单胞结构或者全尺寸结构,难以分析纤维、孔隙、裂纹及界面相等结构随机分布特性的影响。而基于XCT三维重构模型的分析方法,为解决该问题提供了新的思路和技术途径,但同时,如何合理利用该方法提供的丰富微观结构信息,建立高精度的编织结构CMC材料等效导热系数预估模型是未来发展的重要方向之一。
2) 针对CMC热端部件的热分析方法,目前尚处于起步发展阶段,大部分研究简单采用基于模型全局各向异性导热系数的均匀化热分析方法,少数学者在此基础上进一步考虑了涡轮叶片等热端部件的复杂型面,对模型各向异性导热系数空间分布的影响。然而,目前的均匀化热分析方法忽略了编织结构等特征对CMC热端部件内部热量传输机制的影响,且难以获取CMC热端部件温度场的真实信息。而将编织结构直接应用于涡轮叶片等几何尺度较大且结构特征复杂的热端部件时,又会导致计算激增。宏观热分析中如何高效引入 CMC微观尺度信息,建立精度高且工程可应用的 CMC材料热端部件跨尺度热分析方法是目前亟需突破的技术难题。
3) 针对CMC热端部件的冷却结构,考虑到气膜冷却效果本身的非均匀特性,以及CMC材料的非均匀与各向异性特征,会使得CMC材料冷却结构的热量传输及冷却机制变得异常复杂,目前这方面的研究尚处于起步阶段。未来的热分析还需要同CMC热端部件的制造工艺、力学行为分析等进一步紧密结合,实现多物理场联合仿真。
4) 将CMC材料内部细观结构特征与宏观构件进行协同设计以获得高效的热负荷管理是未来一个重要的研究方向。以3D打印技术为代表的先进增材制造技术为其提供了重要技术支撑,同时基于计算机断层扫描的三维重构技术为构建精细化的多尺度几何模型提供了技术支撑,进而为其多尺度热分析方法奠定了基础。

