等残留高度法中的步长精度优化研究

闵 莉，徐冬冬，贾宏博

(沈阳建筑大学机械工程学院，辽宁 沈阳 110168)

五轴数控加工相对于三轴数控加工多了两个旋转轴，这意味着刀具有了更多的自由度，在工件加工中能很大地提升加工精度和加工效率，但随着刀具自由度的增加，数控编程的难度也随之大大增加。刀具轨迹规划作为数控编程的核心环节，目前常用的规划方法有等参数线法[1-2]、截面法[3-5]、等残留高度法[6-9]。等参数线法是让曲面的一个参数保持不变，另一个参数等距离增加产生的曲线作为轨迹线的方法，参数增加的距离通常选择待加工曲面上的最小行距，等参数线法的优点是计算十分简便，实用性非常高，在实际加工中得到普遍应用，缺点是行距选择过于保守，会增加轨迹线的长度，降低加工效率。截面法与等参数线法类似，不同之处在于截面法是用距离相等的一组平面去截待加工曲面，得到的交线就是刀具轨迹线。而等残留高度法是由K.SURESH等提出的，主要思想是让对应刀触点之间的残留高度等于设定值，以此求得加工行距，加工中能提高加工效率、适于曲率变化较大的曲面，是当今运用最广泛的刀具规划方法。

在用等残留高度法对刀具运行轨迹规划时，由于相邻轨迹线对应刀触点之间具有依赖性，容易出现拐点、突变点或造成过切、欠切，针对这些问题，众多科研人员进行了相关研究：赵世田[10]提出一种通过计算残余高度线，进一步增大行距的算法，有效减小了刀具轨迹的总长度；张莹等[11]通过建立机床模型，计算出了刀具的最大走刀步长；王太勇等[12]在传统等残留高度法基础之上提出了一种高精度刀轨误差补偿算法，该算法能提高相邻刀具轨迹上刀位点参数值的计算精度；S.G.LEE等[13]用等残留高度法规划出了轨迹线，并提出了行距计算方法；A.CAN等[14]充分考虑了曲面的几何特征，对曲率不同的区域选择不同的刀具半径，以减小走刀走长度和避免过切。此外，很多依据其他不同原理的刀具轨迹规划方法也被提出，C.J.CHIOU[15]等由零件几何形状和刀具几何形状相结合，构造出加工能量场，进一步找到最大加工带宽方向，并作为走刀方向，生成刀具路径，与等参数线法与等截面法相比能显著提高加工效率和工件的表面光洁度；S.DING等[16-17]在截面法的基础上，提出一种自适应算法，在不同的加工区域选择合适的截面间距。

在上述研究基础上，笔者针对等残留高度法中走刀步长在偏置轨迹线上不受约束的问题进行研究，由等残留高等法计算规则设计出偏置轨迹线上走刀步长的计算方法，并提出步长误差变化率这一概念，用以直观地观察步长的变化情况，最后根据步长误差变化率的变化规律，设计出步长累积误差的消除方法；经试验验证，该方法消除了等残留高度法偏置过程中产生的累积误差，有效地保证了加工精度。

1 曲面构造理论

非均匀有理B样条(NURBS)[18-19]是由B样条、有理B样条逐渐优化发展而来，能精确地表示空间中的点、线和曲面，并具有较强的灵活性和功能性，在曲面建模中得到广泛应用。设构造的曲面为S(u,v)，如式(1)所示：

(1)

式中：di,j为控制顶点；wi,j为权因子；Ni,j(u)为沿u方向的第i个j次规范B样条基函数；Nj,i(v)为沿v方向的第j个i次规范B样条基函数。

(2)

式中：Ⅰ、Ⅱ分别是曲面的第一、第二基本量函数。

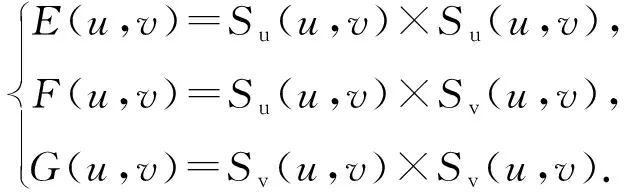
(3)

(4)

式中：E、F、G、L、M、N等参数可由式(3)、(4)中的函数关系来表示。

在NURBS曲面中，通常用定义k1、k2为X方向和Y方向的主曲率。其中，k1为最小主曲率，k2为最大主曲率。平均曲率H和高斯曲率K可以用k1、k2来表示：

(5)

(6)

平均曲率和高斯曲率主要用来判断曲面的凹凸。

2 刀触点之间相关参数的计算

2.1 刀具走刀步长的计算

图1为曲面S(u,v)的截面示意图。其中，P0、P1为两个相邻的刀触点，ε为允许的弓高误差。

图1 走刀步长示意图Fig.1 Schematic diagram of cutting step length

由此可算出走刀步长：

(7)

式中：Rn为刀具在P0处的法曲率半径，可由下式计算得到：

(8)

式中：ρ为P0处沿走刀方向的法曲率。

2.2 加工行距的计算

计算加工行距时，首先判断曲面的凹凸性，然后分别在平面、凹面和凸面上计算行距。当曲面为双曲面时，根据刀具走刀方向上的曲率来判断曲面凹凸性。

设球头刀刀头半径为r、加工后残留高度为h、刀触点短程线方向曲率半径为Rn，据下图所示的几何关系,可算出加工行距L。

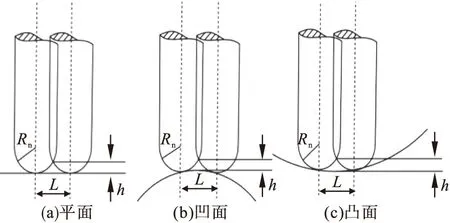
图2 加工行距的确定Fig.2 Determination of path interval

当加工曲面为平面时：

(9)

当加工曲面为凹面时：

(10)

当加工曲面为凸面时：

(11)

3 步长误差的形成与消除

3.1 步长误差的形成

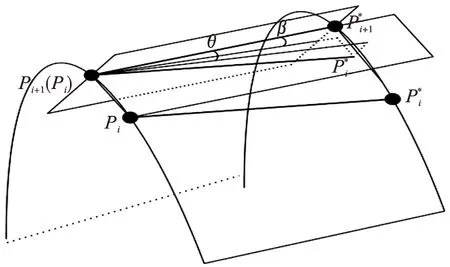
图3 曲面上的刀具轨迹Fig.3 Tool-path on surface

(12)

由式(12)[6]可知，等残留高等法在偏置过程中走刀步长的主要受行距大小、加工曲面起伏、短程线方向等因素影响。

(13)

实际加工时，为保证工件的表面质量，在规划轨迹线过程中对轨迹线的光顺度有要求[20]，在保证刀具轨迹光顺的前提下，根据短程线定义[21]可得θ≈0o，所以：

g′≈

(14)

由式(13)、(14)可知g′≥g，并且只有β=0、Li=Li+1时，g′=g。

由此可知，等残留高度法规划出的轨迹线，走刀步长会在上一条刀轨增加的基础上继续增加，形成累积误差。

3.2 步长误差的消除

为减小或消除步长误差，需对传统等残留高度法加以改进。设刀轨上刀触点间实际走刀步长为g2,理论走刀步长为g1,步长的误差变化率用α表示，α的计算方法如式(15)所示:

(15)

其中，g1可由式(7)计算得到。

设定阈值ψ，当相邻两个刀触点同时满足α>ψ时，移动刀触点的位置，可以减小走刀步长。

为提高效率，从初始刀触点开始，每隔若干点提取一个采样点，并计算该采样点的α值，直到该轨迹最后一个刀触点。其中，两相邻采样点间刀触点的数量可根据曲面实际曲率适当调整。

设Pi、Pj为轨迹线上相邻的两个采样点，且α值同时满足α>ψ，为消除两个采样点间步长的误差，现使用加权平均法均匀减小采样点间的走刀步长。计算方法如下：

(16)

图4为一段刀具轨迹线，P0、P1、P2、P3、P4、P5为相邻的刀触点，P0、P5为刀轨上两个相邻的采样点。

图4 原始刀具轨迹Fig.4 Original tool-path

图5 改进后的刀具轨迹Fig.5 Improved tool-path

3.3 步长累积误差消除算法

步长累积误差消除算法中，阈值参数的大小依据工件加工精度要求来选择，采样点依据相邻刀触点间步长误差变化率的大小来选择。

Step1：选取待加工曲面边长较长的一个边作为初始的轨迹线，按要求的加工精度，选择步长规划算法对初始轨迹线进行离散，得到一系列刀触点。

Step2：因初始轨迹线上刀触点是由步长规划算法确定的，肯定满足加工精度，可直接进行偏置，规划下一条刀具轨迹。

Step3：在第二条轨迹线上，把第一个刀触点设为采样点，隔若干点再选一个采样点，并计算采样点间的α值。

Step4：当相邻两个采样点误差变化率都比阈值大，则执行步长累积误差消除算法，若两采样点不同时大于阈值，则在后续轨迹线段上继续选取采样点，直至覆盖最后一个刀触点。

Step5：继续偏置下一条轨迹线，直至轨迹线覆盖整个曲面。

算法的具体流程如图6所示。

图6 算法流程图Fig.6 Algorithm flowchart

4 实验验证

取图7所示的曲面做仿真实验，选取的刀具类型为球头刀，刀头半径为5 mm，残留弓高ε=0.02 mm，等残留高度h=0.5 mm，阈值参数ψ设定为0.05。

图7 加工曲面Fig.7 Machining surface

传统的等残留高度法生成的轨迹线如图8所示。在图8所示的轨迹线基础上，用步长累积误差消除算法进行优化，为对比优化后的效果，取优化前后的刀具轨迹在XOY平面投影图，取图区域为X×Y=70 mm×100 mm，轨迹线如图9所示。

图8 传统刀具轨迹Fig.8 Traditional tool path

通过对比可以发现，图9(b)比图9(a)的刀触点由左至右逐渐增加，这是因为随着不断的偏置，步长误差不断累积增加，有相邻采样点步长误差变化率超过了设定的阈值参数，通过执行步长误差累积消除根据笔者所提算法设置，此时会根据式(16)移动相应刀触点，并对空缺位置补充刀触点，以缩短走刀步长，由此控制了偏置中步长累积增加。

图9 刀轨细节图Fig.9 Details of tool path

为进一步验证实际优化效果，分别选取图9(a)、(b)中的后三条完整轨迹线α值对比，如图10所示。

图10 优化前后α值的变化Fig.10 The change of α before and after optimization

把图10(a)和表1中的数据对照分析，可以清楚地看出第10、第11条传统轨迹线的步长误差变化率都在前一条轨迹线的基础上继续增加，最大已接近0.3，走刀步长严重失控。

对图10(b)进行分析，发现优化后轨迹线的α值多分布在-0.05～0.05；再结合表1中优化前后的|α|值数据，可以发现优化后三条刀具轨迹的|α|值之和比传统的刀具轨迹分别降低了91.3%、90.84%、89.97%，这说明步长累积误差的消除取得了良好效果。

表1 每条轨迹|α|值之和Table 1 Summation of|α|for each tool-path

5 结 论

(1)在用传统等残留高度法对曲率变化较小的曲面进行刀具轨迹规划时，走刀步长误差变化率会在相邻轨迹线间不断积累。

(2)通过执行步长累积误差消除算法，把步长误差变化率约束在一个区间内，从而控制了走刀步长。

(3)按照笔者所提方法调整轨迹线上刀触点的数量和位置，消除了相邻轨迹线间刀触点一一对应的关系，减小了轨迹线间的依赖性。

(4)经过执行走刀步长累积误差消除算法，刀触点还是分布在原来的刀具轨迹上，优化后刀具轨迹方向、总长度基本没有改变，进一步保证了在提高加工精度的同时加工效率与之前保持一致。