基于FF-MILS和UKF算法的锂电池SOC估算

黄敬尧，李凌峰，张 扬，宋轩宇

(1.三峡大学电气与新能源学院，湖北宜昌 443002；2.湖北能源集团鄂州发电有限公司，湖北鄂州 436000)

近年来，锂离子电池被广泛运用到了电动汽车等生活领域中，但它也有许多瓶颈限制其发展[1]。电池管理系统(battery management system,BMS)通过测量电池外部参数预估其内部状态从而对其工作行为进行管理，包含了均衡电路、温度控制、荷电状态(SOC)等[2]。BMS 的有效管理可提高电池工作效率，从而延长一个充电周期内的行驶里程；也能迅速调整电池工作状态，避免故障，从而增加了锂离子电池组的寿命。而这些功能的实现，都基于BMS 对电池状态估算是否足够准确。

荷电状态(SOC)是电池的可用容量，是十分关键的状态参数，它可以被用来监测并控制电池的工作状态，预测车辆的行驶里程等[3]。但是它不会被直接观测得到，仅能通过采集相关电池参数，建立模型，利用估算算法获得。递推最小二乘法(RLS)是常用的在线辨识方法之一。该算法具备在线识别参数的能力，且算法简单，精确度较高，但会出现数据饱和问题。遗忘因子递推最小二乘法(FFRLS)在其基础上引入了遗忘因子，在迭代过程中用降低旧数据影响的方法来提高新数据的利用率，从而能够很好地解决数据饱和的问题。但其要求系统输入具有平稳性和遍历性，难以实际应用。且初值的设立对算法的动态响应度影响较大，使其不能精确跟踪时变参数。本文在FFRLS 之上引入遗忘因子多新息最小二乘法(forgetting factor multi-innovation least square,FF-MILS)作为所选模型的参数辨识算法[4-5]。将标量新息扩展为向量新息或者矩阵新息，强化参数新息的利用并添加遗忘因子，加速算法对误差的收敛，提高对电池参数的辨识精度。

基于以上考虑，为解决电池模型的实时性与荷电状态估算的准确性，本文推导了二阶RC 电路的离散型状态空间方程，做实验得到了OCV-SOC关系，用模型参数在线辨识的遗忘因子多新息最小二乘法(FF-MILS)结合无迹卡尔曼滤波(unscented kalman filter,UKF)[6]对锂离子电池在线估算，在多种工况实验与仿真中校验了该算法是否可行。

1 锂电池数学模型的建立

1.1 电池模型的选取

由文献[2]可知荷电状态(SOC)的定义公式如下：

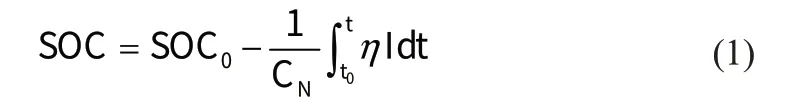
锂离子电池等效电路模型与电化学模型不同[5-9]，它是由电路原理推导出常微分方程建立，更便于计算，且精度也能够满足需求。本文通过比对后采用二阶RC 等效电路，如图1所示。

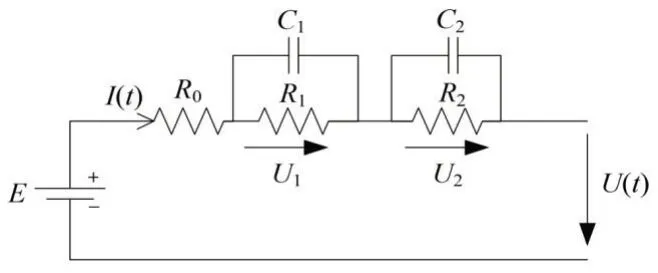
图1 锂电池二阶RC等效电路

当电池发生极化现象时，有图中所示模型参数。电流I(t)与端电压U(t)都是可以通过传感器直接测量得到的状态量，该数学模型的具体函数关系：

联立式(1)与式(2)可得该模型的状态空间方程并离散化得到：

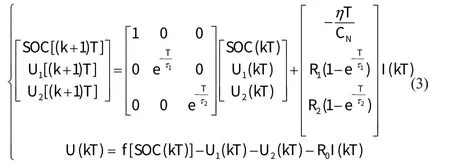
1.2 OCV-SOC 测试

在静置条件下，采用时安积分实验获取SOC与OCV的拟合函数。选用额定容量为30 Ah 的锂离子电池在常温(25 ℃)中进行标准放电电流0.5C恒流放电至放出容量达到标准容量的10%，停止放电并静置2 h 后记录开路电压。重复以上步骤，可以得到该电池测试数据如表1 所示。

表1 OCV-SOC 测试

所记录数据导入MATLAB 的工作区通过plot 函数得到充电与放电OCV-SOC关系如图2 所示。

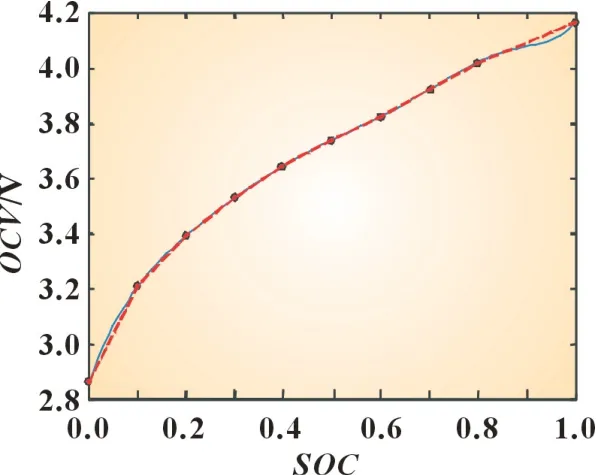
图2 OCV-SOC拟合曲线

将所得数据通过cftool 工具箱拟合，得出了电池电动势E(t)与荷电状态SOC之间的拟合函数关系如下：

1.3 模型参数在线辨识

RLS 辨识算法基于不断采样所获得观测值与迭代递推所获的估计值之间误差对估算结果不断修正，直至出现最优估计结果。其对二阶RC 等效模型参数辨识具体步骤如下：

首先对图1 进行拉氏变换：

将电压差E(s)-U(s)作为输入，I(s)作为输出，作系统的传递函数为：

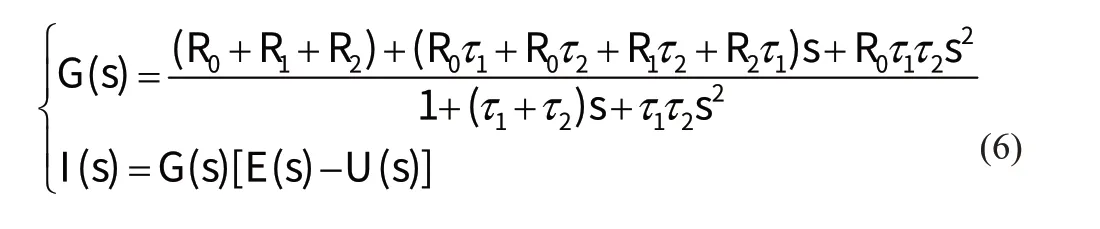
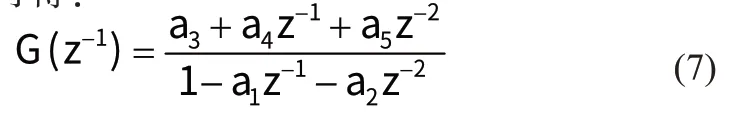
式中：a1、a2、a3、a4、a5为相应的待定系数，将上式转化成差分方程有：

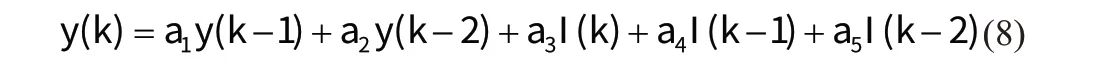
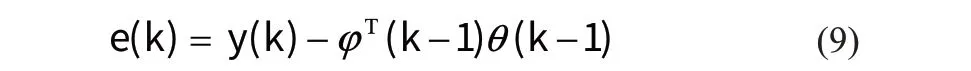
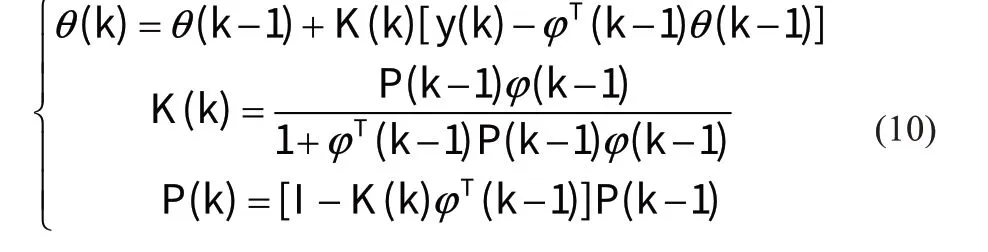
式中：I为同型单位矩阵；P(k)为k时刻的协方差矩阵；新息与其校正增益项K(k)之积加上k－1 时刻的最优估计便是k时刻的最优估计参数θ(k)。由于：

可见，随着采样次数变多，P(k)将逐渐趋近0，由式(9)可知增益矩阵K(k)同样会变得越来越趋近0，便会导致新的采样值对最优估计结果的改进失效，因而出现了数据饱和的问题。向递推最小二乘法中引入遗忘因子，缓解数据饱和现象，实现参数在线辨识。具体递推公式如下：

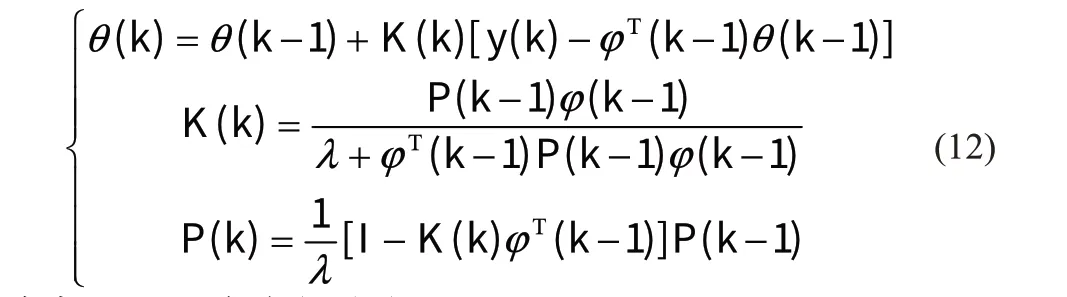
式中：l=0.99 为遗忘因子。

当对锂电池采样的时候，一次仅能够得到一组电池的电压电流数据，并且对初始参数的设置会存在误差较大的情况，这样就会导致辨识的初期无法很好地跟踪电池参数，甚至在采样次数少的情况下会对最终辨识结果产生较大误差。多新息遗忘因子最小二乘法获取新息向量，并对其充分利用，最终达到了对误差的快速收敛。将标量e(k)扩展成长度为p的向量E(p,k)。

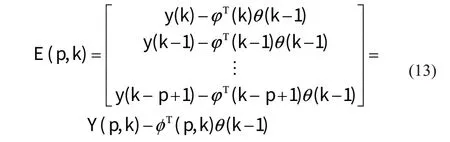
此时，得到扩展后的输出向量与堆积数据的矩阵分别为：

最终有如下递推关系：

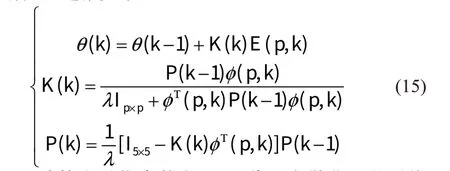
由式(15)计算出最优参数向量θ，代入离散化后的系统传递函数式(7)，由式(6)和(7)对应系数相等可得G(s)的模型参数辨识方程：式中：T为采样周期，得出二阶等效电路模型的每个参数，为接下来荷电状态的估算算法提供了准确数据，将OCV-SOC拟合函数关系导入辨识流程，通过电流参数与初始SOC进行模型动态参数的辨识。具体步骤如图3。

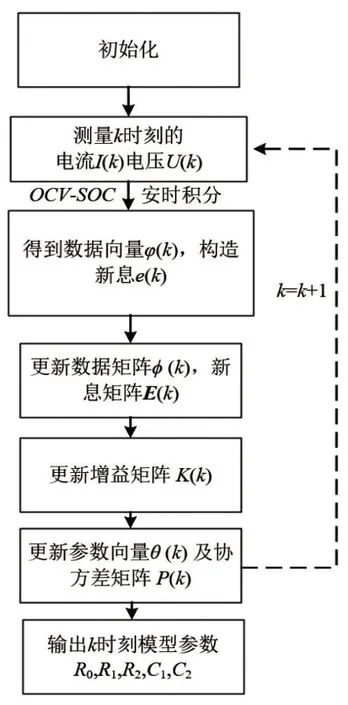
图3 FF-MILS辨识流程

2 电池SOC 的估算

电池SOC的估算采用无迹卡尔曼滤波算法。

无迹卡尔曼滤波(unscented kalman filter,UKF)适用于非线性系统。首先，它不需要考虑非线性函数的连续性及系统阶数。它利用采样点近似逼近系统状态变量，从而进一步提升了滤波估计的稳定性与高精度。UT 变换[10]是无迹卡尔曼滤波最重要的部分，它主要通过状态向量的均值X与协方差矩阵PXX，利用采样点及函数的映射关系获取量变换后的均值Y与协方差矩阵PYY。

在式(3)离散型状态空间模型的基础上添加互不相关且服从正态分布的系统激励噪声序列Wk－1与量测噪声序列Vk，构成了噪声可加型的非线性系统方程如下：

将此时的荷电状态与极化电压组成状态向量Xk+1，端电压看成量测向量Zk，状态量Ak由系统更新电流及模型参数Bk后计算系统方程来获取，量测量则可以直接利用测量得到。构建如下对应关系：

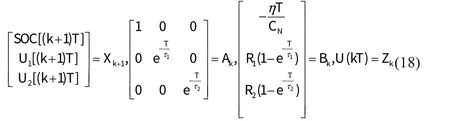
设t=k时刻有如下状态方程与量测方程：

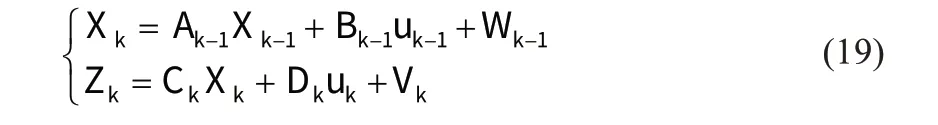
利用无迹卡尔曼滤波算法对式(19)所示系统的状态估计步骤如下：

第一步：初始化设置状态量及协方差矩阵。

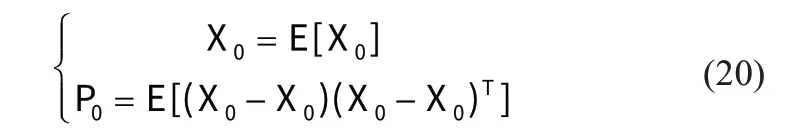
第二步：根据UT变换，计算k-1时刻的2n+1个s 样本点。

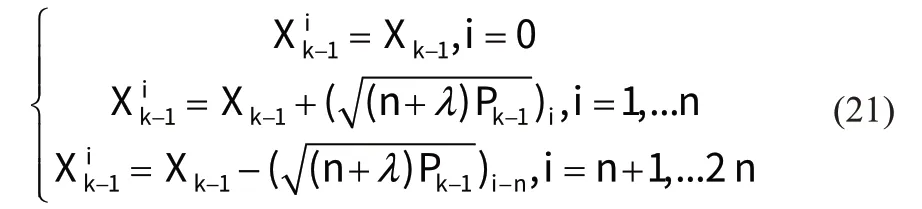
第三步：基于UT 变换后的采样点计算k时刻的一步预测模型值，完成一步预测状态与一步预测协方差的时间更新过程。

式中：Qk为系统激励噪声序列的方差阵，初始化设置为10－6I；为均值权值，为方差权值，可以通过下式计算获取。经仿真调试后，取l=2，a=0.001，b=2。

第四步：利用一步预测状态作无迹变换计算k时刻的一步预测样本点。

第五步：求取协方差矩阵。

其中权重矩阵的求取方式同前，Rk为量测噪声序列，初始值取0.01，量测量的估算通过一步预测样本点的非线性映射加权平均获取，如下所示：

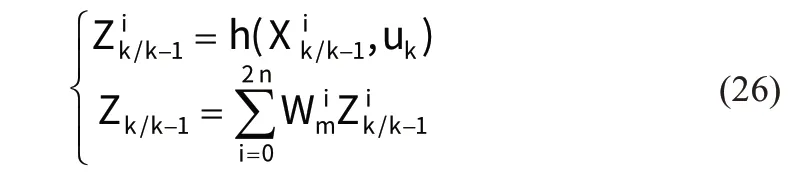
第六步：计算增益矩阵。

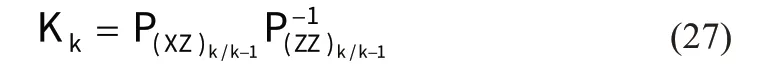
第七步：完成该时刻的最优估计，并更新估计协方差。

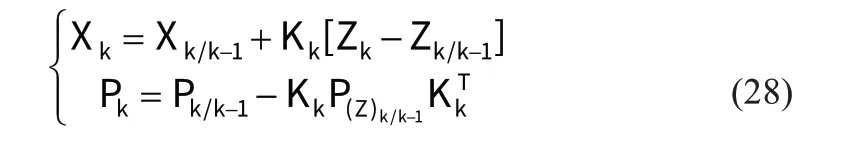
以上便是UKF 获取最佳状态估计的循环迭代过程。在利用UKF 算法求解荷电状态的时候还需要代入模型参数，一个迭代周期的具体过程如图4。

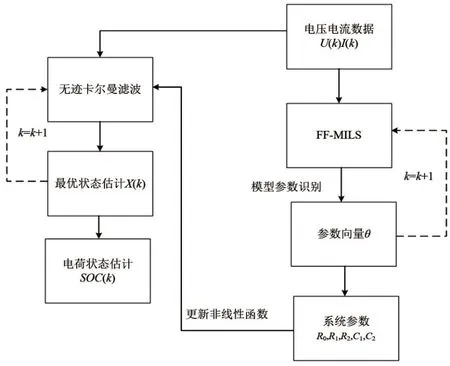
图4 SOC估算过程

3 SOC 估算的仿真验证

3.1 参数识别精度验证

为了验证所提FF-MILS 和UKF 的锂离子电池SOC在线估计算法可行性和精确性，本文设计了标定实验得到OCVSOC关系式以及城市测力计驾驶计划(urban dynamometer driving schedule，UDDS)实验对算法进行验证。UDDS 实验参照了汽车行驶过程中加速、均速、减速、怠速等状态。将上述的工况进行拆分，再相互间隔组合一起对锂电池进行循环放电。图5 为工况电流数据曲线图。图6 为容量30 Ah 的锂电池经过21 次UDDS 循环实验后SOC趋于0 的工况电压实测数据图。

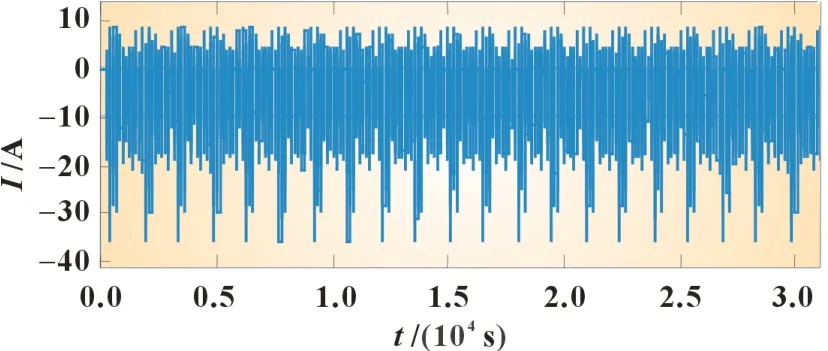
图5 UDDS工况电流曲线

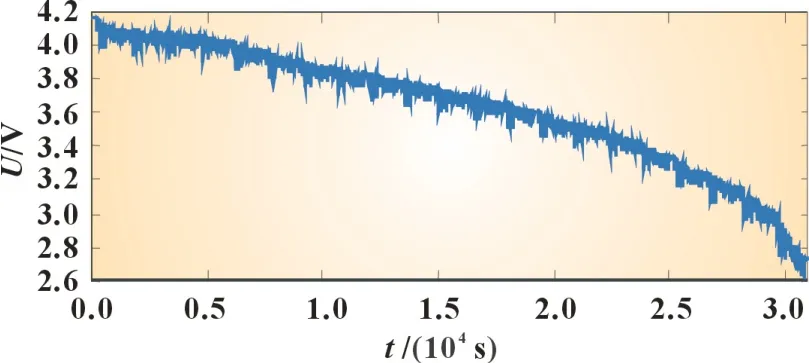
图6 UDDS工况端电压图

为了对比FFRLS 算法与FF-MILS 算法对二阶RC 等效电路模型的端电压估计结果，在MATLAB 里搭建Simulink 仿真模型。图7 是一个UDDS 工况周期内，FFRLS 算法和FFMILS 算法在线估计的端电压与真实端电压的比较。算法的遗忘因子均取0.99。图8 是两种算法与真实值误差对比图。

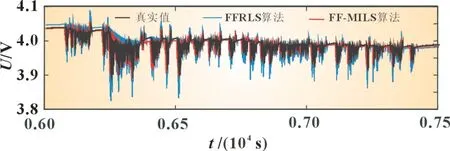
图7 端电压估算对比图

图8 端电压误差对比图

由图8 可知，在初值SOC均设定为1 时，两种算法的收敛速度都比较快。收敛后可知，在UDDS 工况周期内，FFRLS算法的最大误差为0.2 V，本文算法的最大误差为0.04 V，精度显著提高。在最后一个UDDS 工况周期内，锂电池的端电压变化灵敏，稳定性较差，遗忘因子较大，出现较大波动。本文算法通过新息的反馈，实现闭环修正，整体误差曲线波动较FFRLS 要好，验证了FF-MILS 算法的鲁棒性能良好。

3.2 SOC 估计精度验证

实验采用FF-MILS 算法参数识别，通过安时积分得到理想SOC值，分别使用恒流放电工况以及上述UDDS 工况进行SOC估算。使用UKF 算法与EKF 算法得出的SOC，与真实值进行误差对比，验证上述联合算法的可行性。

图9 为脉冲放电工况下两种算法的SOC估计对比图及其误差图。图10 为两种算法在该工况下的误差对比。图中可以看到基于UKF 算法的SOC值更接近真实值。且能更快地跟踪时间SOC的值。在SOC误差对比中，基于UKF 算法的误差要比EKF 误差小，在恒流放电工况下UKF 算法的最大误差不超过2%，EKF 算法的最大误差超过8%。UKF 算法稳定性能更好，精度更佳。

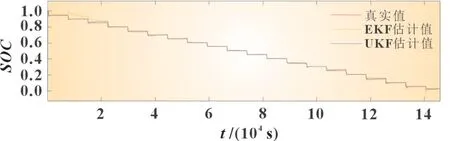
图9 恒流放电工况SOC估计结果图

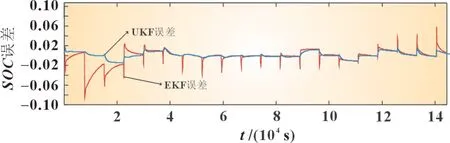
图10 恒流放电工况SOC估计误差图

图11 为UDDS 电流激励下，分别使用EKF 算法和UKF算法计算该锂离子电池的SOC，与真实值的对比图。图12 则为两种算法的误差对比。随着迭代次数的增加、修正系数不断更新，UKF 算法误差基本稳定在2%以内。EKF 算法因为采用一阶泰勒展开的近似处理造成估算误差，计算复杂，运行稳定性差，收敛速度较慢，估计误差在4%左右。本文以UDDS 复杂工况为研究过程，不同倍率充、放电及搁置，使得动力电池内部化学反应变化剧烈，对等效模型参数更新速度和精度提出较高要求，通过联合FF-MILS 算法的参数识别和UKF 算法的SOC估计，联合算法精度符合现BMS 设计要求。

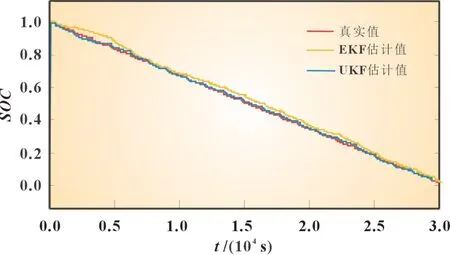
图11 UDDS电流激励SOC估计结果图

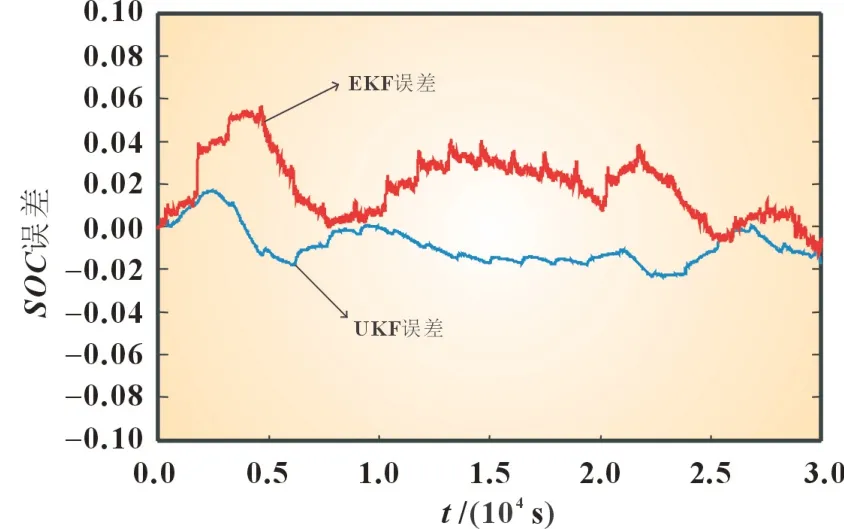
图12 UDDS电流激励工况SOC估计误差图

3.3 算法收敛性的验证

为进一步验证联合算法对误差的收敛性，这里将初始SOC设置为0.8，将锂电池1C恒流放电的实验数据代入仿真程序，所得到的SOC估测结果及误差如图13 所示。可以看见，在初始误差为20%的情况下，联合算法很快修正了估测值，约在100 s 以后就追踪到了理论值附近，从而说明了联合算法对误差起到了一定的收敛作用。

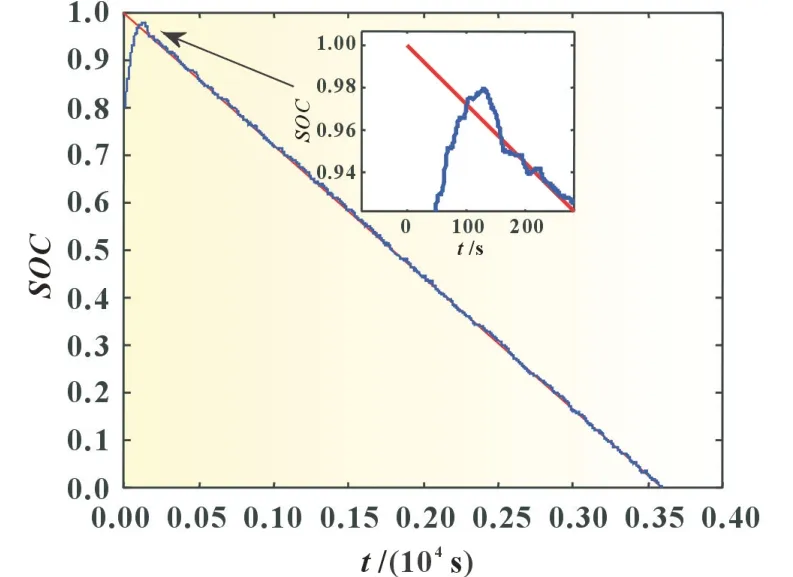
图13 初值为0.8时的SOC估测结果

4 结语

本文以锂离子电池的二阶电路模型为例，采用FF-MILS对模型进行参数准确辨识，将识别参数进行无迹卡尔曼滤波得到最优估计，完成了联合算法对锂离子电池的SOC在线估计。就模型参数辨识而言，其比传统RLS 算法具有更高的精度。然后利用UKF 算法对锂离子电池荷电状态进行估算，其实时性、精确性及鲁棒性均优于EKF 算法，满足实际工程需求。文中着重于常温状态下的状态估计，且算法执行步骤过多，今后主要研究温度影响的电池SOC估计，并将系统简化为分数阶模型，提高系统性能。