锂离子电池剩余寿命间接预测方法研究
陈 万,蔡艳平,苏延召,姜 柯,黄 华
(火箭军工程大学,陕西西安 710025)
锂离子电池已被广泛应用于民用和军用领域,因此其在工程应用中的安全性成为人们关注的焦点[1-2]。预测与健康管理(prognostics and health management,PHM)技术能够有效监控锂离子电池的健康状态,提高电池工作时的安全性,其中剩余寿命(remaining useful life,RUL)预测是实现PHM 的基础,因此成为当前研究的热点。
电池性能退化最明显的特征就是电池容量逐渐变小,内阻逐渐变大,因此电池容量和内阻是表征锂离子电池健康状态(state of health,SOH)的直接健康因子(health index,HI)。目前大多数锂离子电池RUL预测的研究都是采用容量和内阻作为HI[3-4],然而容量和内阻大多数情况下只能在实验的条件下才能获得。对于实际工作状态下的锂离子电池,其内阻监测比较困难并且测量费用较高;此外当前容量的获取方法主要是采用基于监测电压电流等参数的安时法,实际应用中存在累积误差,并且由于实际工作中的锂离子电池一般不会处于完全充放电的工作状态,因此采用安时法估计的容量并不准确。可见基于容量和内阻的RUL预测方法并不适用于工作状态下的锂离子电池,基于此,有学者提出采用易于测量的电池特征参数来实现锂离子电池RUL间接预测[5-7]。Liu等[8]通过提取电池放电过程中的电压电流特征获得了等压降充电时间序列,采用Box-Cox 变换优化提取的HI,最后采用优化的相关向量机实现了锂离子电池RUL间接预测。但有学者提出电池的放电状态会因工作状态的不同而变化,充电状态相对来说更加稳定,因此从充电过程中提取间接HI更符合实际[9-10]。Wang 等通过分析发现恒压充电过程中的电流变化与电池SOH 相关并构建出HI实现了锂离子电池RUL预测。因此利用充电过程中的特征参数来构建HI是当前研究的热点,但目前RUL间接预测还存在以下几个问题:一是基于单一HI的预测方法鲁棒性不高;二是构建HI时忽略了实际中电池不会完全充放电的情况;三是构建HI时电压电流选取范围的优化问题。
基于上述问题,本文提出了一种基于优化的融合型HI的RUL间接预测方法。该方法具有以下几个优势:一是考虑到充电状态更加稳定,本文从充电过程中提取HI,同时在HI的提取过程中避免了电池的电压电流处于完全充放电的状态,更加符合实际工作状态的电池;二是通过自适应HI提取方法优化了HI提取过程中电压电流的范围,同时通过两个HI的组合和Box-Cox 变换来提高HI与容量的线性关系;三是将交叉验证(cross validation,CV) 和粒子群优化(particle swarm optimization,PSO)算法引入最小二乘支持向量机(least squaressupport vector machine,LS-SVM),实现了LS-SVM 超参数的自适应选择,提高了预测算法对不同训练集的适应能力。
1 融合型HI 的构建与优化方法
1.1 锂离子电池的老化数据
数据采用美国国家航空航天局(National Aeronautics and Space Administration,NASA)公开的数据集。NASA 使用Li-ion 18650 型号电池进行了容量衰退实验并获得了四组老化数据,分别对应四块电池:B0005、B0006、B0007 和B0018。电池的额定容量为2 Ah,实验在室温(24 ℃)下进行,其实验过程如下:
(1)充电:首先进行恒流(1.5 A)充电,然后当电池电压达到4.2 V 后,改为恒压充电,当充电电流下降到0.02 A 时充电完成。
(2)放电:恒流(2 A)放电直到B0005、B0006、B0007 和B0018 的电压分别下降到2.7、2.5、2.2 和2.5 V。
1.2 单一HI 的提取方法
电池的充电状态相对于放电状态来说更加稳定,因此本文通过分析充电过程中的电流电压变化提出了一种基于PSO 算法的自适应HI构建方法。图1 和图2 是B0007 在充电过程中电压电流的变化趋势,从图中可以看出,可以构建的HI有等电压升充电时间序列、恒流充电时间序列、等电流降充电时间序列。其中恒流充电时间序列的计时起点为t=0 s,即要求上一周期电池完全放电,而实际工作中电池一般不会完全放电,因此该HI在实际中很难获取。因此下面对其他两个时间序列进行分析,为了方便描述,将等电压升充电时间序列简称为HI1,等电流降充电时间序列简称为HI2。

图1 不同充电周期的充电电压变化曲线

图2 不同充电周期的充电电流变化曲线
HI1的构建方法:利用PSO 算法获得一个最优电压变化区间,计算电池在一个充电周期的充电过程中电压变化经过该区间的时间,该时间即为对应周期的HI1。图1 中展示了第40个循环周期时HI1的构建过程。然后计算不同充电周期的HI1并按周期进行组合,最终构建出HI1。同时电压范围的选择需要避免电池的完全充放电过程,从图1 可以发现,充电后的极短时间内电池的电压上升至3.85 V 以上,因此本文电压变化范围的下限定义为3.95 V;充电截止电压为4.2 V,考虑测量误差带来的波动,电压变化范围的上限定义为4.18 V。
HI2的构建方法:利用PSO 算法获得一个最优电流变化区间,计算电池在一个充电周期的充电过程中电流变化经过该区间的时间,该时间即为对应周期的HI2。图2 中展示了第160 个循环周期时HI2的构建过程。然后计算不同充电周期的HI2并按周期进行组合,最终构建出HI2。同时电流范围的选择需要避免电池的完全充放电过程,实验中电池充电结束的条件为充电电流下降到0.02 A,因此本文电流变化范围的下限定义为0.2 A;恒流充电电流为1.5 A,考虑测量误差带来的波动,电流变化上限定义为1.48 A。
1.3 HI 的优化与融合方法
单一HI有时无法准确表征电池的健康状态,因此本文提出了一种基于PSO 算法的融合型HI构建方法。通过HI1和HI2的线性组合构建新的融合型HI,这里融合型HI简称HI3:
当HI1和HI2与容量的正负相关性相同:

当HI1和HI2与容量的正负相关性相反:

式中:a,b代表需要优化的参数,采用PSO 算法实现两个参数的优化。
为了增强HI3与容量的相关性,本文提出了一种基于PSO算法的Box-Cox 变换来实现HI3的优化。Box-Cox 变换通常用于提高两组数据的线性相关性,其变换过程如下:

式中:yi代表原序列,y(λ)代表变换后的序列。可以看到λ不同变换的结果也不相同,因此如何选择一个最优的参数是Box-Cox 变换的关键,本文利用PSO 算法实现参数的最优化选择。
1.4 HI 构建方法有效性分析
本文HI的构建流程如图3 所示,这里优化后的融合型HI简称为HI4:

图3 HI的构建流程
Pearson 相关系数分析法可以定量表示两组序列之间的线性关系,其计算方法如下:
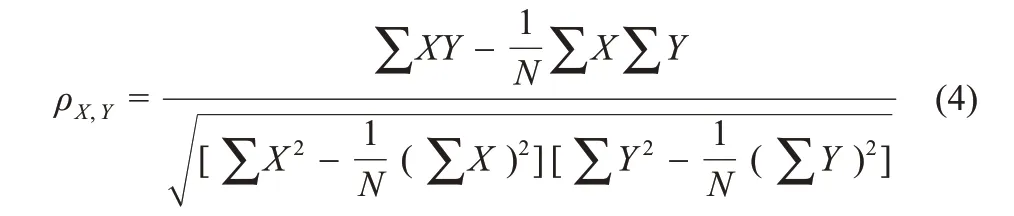
式中:X和Y代表两组序列;N代表序列的长度;ρ的取值范围为[-1,1],ρ的绝对值越大代表两组序列的线性相关性越强,其中ρ>0 代表正相关,ρ<0 代表负相关。
利用离线电池B0007 的数据进行HI构建方法的有效性分析。首先根据HI构建方法获得HI1、HI2、HI3和HI4,并利用Pearson 相关系数分析法定量分析HI与容量的线性关系,结果如表1 所示。

表1 电池B0007的HI 与容量的线性关系
从表1 可以看出,四个HI与容量都具有较强的线性相关性,其中HI2与容量为负相关,其余为正相关;HI1到HI4的Pearson 相关系数的绝对值在递增,表明HI4与容量的线性相关性最好,验证了本文提出的HI构建和优化方法的有效性。
2 PSO 优化LS-SVM
LS-SVM 不仅继承了SVM 全局最优和小样本的特点,而且将SVM 中的凸二次规划求解问题转换为线性方程组求解问题,大大减小了算法的计算量,更加适合RUL间接预测。LS-SVM 的标准形式如下:

式中:w、b代表系数;γ代表正则化参数;e代表误差;h(x)代表低维到高维的映射关系。
求解过程中会使用到核函数,其中径向基核函数在非线性问题求解中使用最广泛,其表达式如下:

式中:σ代表核函数带宽。本文采用核函数为径向基核函数的LS-SVM 算法实现RUL预测。但LS-SVM 的性能与参数γ和σ的设置直接相关,因此本文将k折交叉验证方法和PSO算法引入LS-SVM 提出了PSO-LS-SVM 算法。其中k的取值一般大于2,当数据集较小时,k也可以取2,本文中k的取值为3。因此算法流程如图4 所示。

图4 PSO-LS-SVM算法流程
3 基于间接HI 和PSO-LS-SVM 的锂离子电池RUL 间接预测方法
基于间接HI和PSO-LS-SVM 的锂离子电池RUL间接预测实现步骤如下:
Step1:分析离线电池的退化数据。提取离线电池的等电压降充电时间序列和等电流降充电时间序列,利用HI的构建方法获得HI4。
Step2:获取HI与容量的关系模型。通过上述分析可知,HI与容量具有较强的线性关系,因此将离线电池的HI作为PSO-LS-SVM 的输入,容量作为输出,从而构建HI与容量的线性关系模型。
Step3:设置预测起点。首先采用HI构建方法从在线电池中提取HI,然后将预测起点之前的HI作为训练集。
Step4:对HI进行预测。将训练集输入到PSO-LS-SVM中获得HI预测模型,通过外推模型获得HI的预测值。
Step5:计算预测的容量和RUL。通过获得的HI预测值和HI-容量关系模型,计算容量的预测值;然后计算容量小于失效阈值时的循环周期数减去预测起点的值,即为RUL。
因此基于间接HI和PSO-LS-SVM 的锂离子电池RUL间接预测方法实现过程如图5 所示。

图5 锂离子电池RUL间接预测方法实现过程
4 实验验证与结果分析
4.1 HI 构建结果分析
利用HI构建方法从B0005 和B0018 提取了HI4。本文中锂离子电池的失效阈值设置为额定容量的70%,即1.4 Ah,则根据离线电池获得的HI与容量的关系模型可以求得不同HI对应的循环周期,结果如表2 所示,其中AE代表不同HI对应的循环周期与实际循环周期的绝对误差。

表2 不同HI 对应的寿命周期
从表2 可以看出,HI1对应的循环周期与实际值的绝对误差在B0005 中只有5 个周期,然而在B0018 中达到了14 个周期,波动较大;而HI2与HI1类似。HI4对应的循环周期与实际值的绝对误差在B0005 和B0018 中都小于10 个周期,这表明优化的融合型HI的精度优于单一HI。
4.2 基于不同HI 的RUL 预测结果分析
为了验证提出的优化的融合型HI的有效性,本文采用不同HI和PSO-LS-SVM 算法进行RUL间接预测。预测结果采用绝对误差AE进行评价,同时为了便于观察分析,将所有数据进行了归一化处理。文中T代表预测起点,实验具体步骤如下:
(1)预测起点设置为第90 个和第110 个循环周期,即T=90和T=110,采用容量、HI1、HI2、HI3和PSO-LS-SVM 算法实现B0005 的RUL预测,其中T=110 时采用HI4进行RUL预测的结果如图6 所示。

图6 T=110时B0005的预测结果
(2)预测起点设置为第75 个和第85 个循环周期,即T=75和T=85,采用容量、HI1、HI2、HI3和PSO-LS-SVM 算法实现B0018 的RUL预测,其中T=75 时采用HI4进行RUL预测的结果如图7 所示。

图7 T=75时B0018的预测结果
(3)采用AE 评价RUL预测结果,结果如表3 所示。
从图6 和图7 可以看出,HI4能够较好地跟随实际的容量退化过程;同时基于HI4的预测方法获得的预测曲线能够较好地拟合实际退化过程,表明本文提出的HI能够代替容量用于锂离子电池的RUL预测。对比分析表3 中不同HI的RUL预测结果可以发现,采用HI4预测的RUL的绝对误差比HI1和HI2的更小,表明本文提出的预测方法比基于单一HI的预测方法精度更高;同时在不同预测起点和不同电池中采用HI4预测的RUL的绝对误差变化较小,而HI1和HI2获得的结果的绝对误差变化较大,表明提出的方法具有较好的适应能力。
5 结论
(1)针对锂离子电池容量在线测量困难的问题,提出了一种优化的融合型HI构建方法,并利用B0007 的数据和Pearson相关系数分析法对HI构建方法的有效性进行了验证,最后对比分析了在线电池构建的HI对应的循环周期与实际容量对应的循环周期,结果表明本文提出的HI构建方法构建的HI与容量具有很好的线性关系,同时相比于单HI具有更好的鲁棒性。
(2)针对构建的HI,提出了PSO-LS-SVM 预测算法。其中PSO 算法用于优化LS-SVM 算法的超参数,实验结果表明,优化的算法对不同的预测起点和预测数据具有较好的适应能力。
(3)对比分析了不同电池、不同预测起点下基于不同HI的RUL预测结果,结果表明本文提出的锂离子电池RUL间接预测方法比基于单一HI的预测方法具有更高的精度和鲁棒性。

