基于模糊C均值算法的电力变压器聚类分析

刘丁源，裴 磊，魏 炯，高华锋，蔺庚立，王 勇，郭海涛

(国网宝鸡供电公司，陕西 宝鸡 721004)

为有效解决电力变压器检修不及时或者过度检修的问题，需要以电力变压器健康状态的评估为依据制定具有针对性的电力变压器检修计划。状态评估的前提是对在线监测系统或离线检测系统所获取的电力变压器的观测数据进行有效挖掘，获取足以支撑制定科学检修计划的先验知识[1-3]。随着智能电网和泛在电力物联网建设的普及，与电力变压器运行状态相关的信息已经呈现出数量大、类型多、增速快的特征，这大大增加了数据挖掘的难度[4-6]。为此本文提出使用聚类分析方法对所采集的观测数据进行处理，实现相同健康状态的电力变压器的聚类分组，便于针对不同状态的电力变压器制定不同优先级的检修计划，从而提升电力变压器检修的针对性和合理性，降低检修成本。

本文首先阐述拉普拉斯评分、主成分分析和模糊C均值算法三种算法原理，然后基于三种算法提出电力变压器聚类分析方法，最后使用真实观测数据进行仿真实验以阐明所提方法的具体操作步骤及其有效性。

1 主要算法

1.1 拉普拉斯评分

L=D-K

(1)

特征f的拉普拉斯评分按以下方式计算：

(2)

1.2 主成分分析(PCA)

设X∈Rn×n为包含n个观测变量的矩阵，每个观测向量均由p个观测变量或参数组成，因此可以视为观测空间中的一个点。PCA的目的是探索p变量之间的联系以及观测变量之间的相似性[10-11]。PCA允许构建由主成分组成的欧几里德空间，该线性空间是p个初始变量的线性组合，目的是建立具有最恰当地概括该空间数据结构特征的欧几里德空间。通过PCA还可降低观测向量的维度。通过计算关联矩阵R的向量和特征值，可以获得构成该空间轴的主成分。

(3)

式中，XT为X的转置矩阵。

通过计算方差评估数据惯性。对于任意变量，矩阵R的特征值与变量总数之间的比率表征了该变量所提供的主成分承载的信息量。数据惯性由以下关系式计算：

(4)

式中，λi∈{1，…，p}为矩阵R的特征值。

1.3 模糊C均值算法

无监督分类算法是对数据进行聚类分组而无需类别特征数据[12-15]。聚类技术用于将数据划分为多个组，以便在一个组内数据的关联度很高，而在不同组之间数据的关联度很低。从相似性的标准来看，来自同一组(也称为聚类)的观测值比来自其他聚类的观测值更接近彼此，即将任何观测值分配给其更接近其中心的聚类。相似性准则通常基于距离。模糊C均值算法使用模糊逻辑来定义属于一个类的程度。对于每个组，为每个数据点分配一个介于0和1之间的隶属度。隶属度表示每个数据点属于不同组的概率。

给定多个聚类c，模糊C均值算法将针对模糊隶属度uij和聚类中心cj最小化如式(5)所示的目标函数，将X={x1，…，xn}数据分类为c个模糊聚类。

(5)

式中，m为权重系数，称为“模糊系数”；uij为xi对聚类j的隶属度；xi为矩阵数据中维度为d的第i个观测值；cj为是维数为d的聚类中心j。

隶属度由式(6)给出：

(6)

聚类中心由式(7)给出：

(7)

模糊C均值算法流程为：①随机初始化属于聚类i的xi的隶属度值uij；②计算聚类中心cj；③使用式(6)更新隶属度；④使用式(5)计算目标函数；⑤重复步骤②至④，直到算法收敛为止。

如果式(3)所计算得出的Г值低于预定的阈值，或者已达到迭代的最大数量，则可以认为算法收敛。通过调整模糊系数可以优化聚类之间重叠的程度。

2 聚类分析方法

聚类分析方法的目标是从在给定的有效的观测数据集中识别出具有相似运行状态的电力变压器。聚类分析方法包括4个主要步骤。

(1)评估观测数据集中每个特征的重要性，并选择其中最重要的特征。在模式识别和机器学习领域，已有一些得到公认的有效的特征选择工具，如皮尔逊相关系数[16]、卡方分布[17]和拉普拉斯分数(LS)[18]等。使用这些工具可以根据特征的子集与用户需求的相关程度或重要性展开特征选择。在无监督分类算法中，特征选择相对复杂，因为缺少可以指导搜索相关信息的类标签。基于提升聚类效率、降低数据维度并提高数据的可理解性的考虑，本研究使用LS作为特征选择工具。这种选择带来的另一个好处是LS的实现方式相对简单。在完成所有特征的LS值排序后，即可获得在聚类分析中包含最相关信息的参数的标识。一旦确定了最重要的特征，就可以删除其余特征，然后继续第2步。

(2)使用主成分分析(PCA)来定义一个新的观测变量。所获得的新观测变量由初始观测变量的线性组合组成。根据这些新的观测变量，可以确定观测数据集及其携带的信息量。

(3)将模糊C均值算法应用于观测数据集实现无监督分类。所得聚类是基于数据中的内在关联性形成的。

(4)根据专家知识对每个聚类进行解释，并基于解释结果来制定具有针对性的检修计划。

3 实验结果

实验数据来自国网宝鸡供电公司的33台油浸式电力变压器，型号为SFPS7-120000/220，一次侧电压为220 kV，容量为120 000 kVA，2000年投入使用。数据采集于2019年，数据源为电力公司的电力变压器在线监测系统。观测参数及其含义[19-20]见表1。

表1 观测参数

按照前述的方法，分4个步骤进行聚类分析。

(1)识别每个参数在数据结构中的相关性。各个参数的LS计算结果和排序见表2。

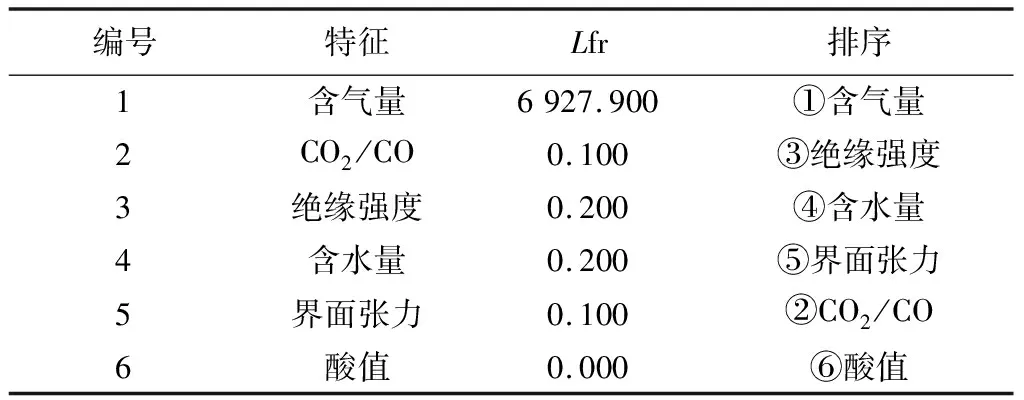
表2 LS的计算结果

(2)通过PCA识别参数空间的轴。在完成LS计算之后，PCA的目标是识别参数空间以及构成该空间的每个轴的重要性。PCA可以更好地造成参数差异的主要原因。

关联矩阵R的特征值和累积方差见表3。根据等式2，基于矩阵R的值可计算得出结果见表4。

表3 轴、特征值、方差贡献率和累积方差贡献率

表4 轴与变量之间的关联

由表4可知，前3个参数为数据集的主要特征。由这3个主要特征的线性组合所得出的变量为参数空间的数轴，并表征为新的观测变量。表4给出了参数在每个数轴上的投影值。图1显示了相对于前2个观测变量的参数空间分布。

图1 变量相关性

(3)基于所确定前3个参数对观测数据使用模糊C均值算法开展聚类分析。聚类结果是将电力变压器分为4组，分别对应A组、B组、C组合D组。每组电力变压器的运行状态将使用专家知识加以解释。在PCA所标识的特征空间中表示所得的4个聚类如图2所示。

图2 基于模糊C均值的聚类结果

(4)对聚类结果进行解释。聚类1中的电力变压器的绝缘质量已经劣化为此需要尽快对绝缘油中杂质进行检查。聚类2中的电力变压器的油质和绝缘性能均可接受，但是溶解气体含量较多。聚类3中的电力变压器的油质和绝缘性能均不理想，需要考虑尽快进行变压器油的更换。聚类4中的电力变压器油的绝缘性能可以接受。

4 结语

电力变压器运维过程中积累的海量观测数据与变压器运行状态之间的关联并非显而易见，为此需要挖掘这种内在关联性以服务电力变压器检修计划的制定。本文提出的电力变压器聚类分析方法，使用PCA方法提取观测数据的主要特征，然后使用基于模糊C聚类算法获取4个特征迥异的变压器组。最后利用电力变压器工程师的专业知识针对不同变压器组进行解释，为制定具有针对性的检修计划提供专业科学指导意见。