基于卷积神经网络的发电机运行状态实时监视

潘 远，陈章国，蔡新雷，杨民京

(1.广东电网有限责任公司电力调度控制中心，广东 广州 510600；2.南京南瑞信息通信科技有限公司，江苏 南京 210003)

由于电力系统互连规模和复杂性的持续增长、可再生能源的扩散和涌入、电力需求的增加，使得电力系统中发电机稳定工作点的控制变得更有难度，导致大规模电力系统事故和大范围停电风险的增大[1-3]。为此，需要进行发电系统暂态稳定性实时监视，以便在出现电力系统波动时快速和准确地识别发电机的运行状态[4-5]。

电力系统暂态稳定性评估的主流方法包括时域仿真法[6]和直接法[7]。时域仿真法需要求解非线性微分代数方程，计算量大，在实时应用场景下对计算资源的要求较高。直接法主要有能量函数计算法，能够给出量化的电力系统稳定值。将系统的势能和动能值与参考值进行比较的能量函数计算方法，在实际应用中无法准确估算实际能量值。基于能量函数的扩展等面积准则[8]、边界轨迹法[9]等方法，虽然计算效率较好，但是仍不够准确。

随着人工智能算法的快速发展，基于数据驱动的技术为发电机组暂态稳定性监视提供了新的解决思路。为此，本文提出一种基于改进卷积神经网络的发电机组运行状态的实时监视框架。该框架利用部署的相量测量单元(PMU)所取得的测量值，包括电压和电流幅值、发电机功角以及系统频率等，构造变量热图作为输入数据，然后使用带有预设池化层的卷积神经网络对图像进行多标签分类，以实现发电机组运行状态的在线识别。

1 卷积神经网络和预测池化层

卷积神经网络是图像分类处理常见的人工智能算法[10-11]，由卷积层、池化层和完全连接层组成。在单标签图像分类应用场景中，卷积神经网络可以有效地处理对齐良好的图像，具备良好的分类性能[12]。然而在多标签图像分类应用场景中，由于会出现错位和遮挡等复杂问题，导致卷积神经网络的分类准确性较差。为此，研究通过预测池化层对分割图像进行特征标签预测，然后使用共享卷积层连接到每个预测图层，最后将不同的单标签预测结果汇总为多标签预测结果[12]。

在卷积层中，通过卷积核从输入数据中提取特征的定义为[13]：

(1)

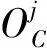
池化层从卷积层中提取重要特征，其输出可表示为[14-15]：

(2)

式中，d()为下采样函数；βj为池化层的第j个系数。

完全连接的层由多个隐藏层组成，其输出通常可以表示为：

(3)

式中，ω为权重系数；σ()为激活函数。

假设vi为第i个预设池化层的输出向量，且vij为vi的第j个分量，则最大池化层可表示为：

(4)

式中，vj可被视为给定图像的第j个类别的预测值。

(5)

式中，M为图像数量。

用于多标签分类的含预测池化层的卷积神经网络在输出层包含2个分类器：①第1个分类器的输出通过softmax函数归一化处理。softmax函数针对每个类别的计算概率分数，这些分数将用于确定每种输入图像的最终分类。②第2个分类器在输出层使用sigmoid激活函数。在输出层的sigmoid激活函数中，某一类别的概率将被建模为伯努利分布。与softmax不同，sigmoid函数不会为所有类别输出的概率分数，而是输出唯一概率。

2 监视框架

发电机运行状态在线监视框架如图1所示。由图1可知，从PMU获得的数据首先用于离线训练卷积神经网络框架。然后将完成训练的框架用于监视在线识别发电机的运行状态，并实时识别影响系统波动的关键发电机组。

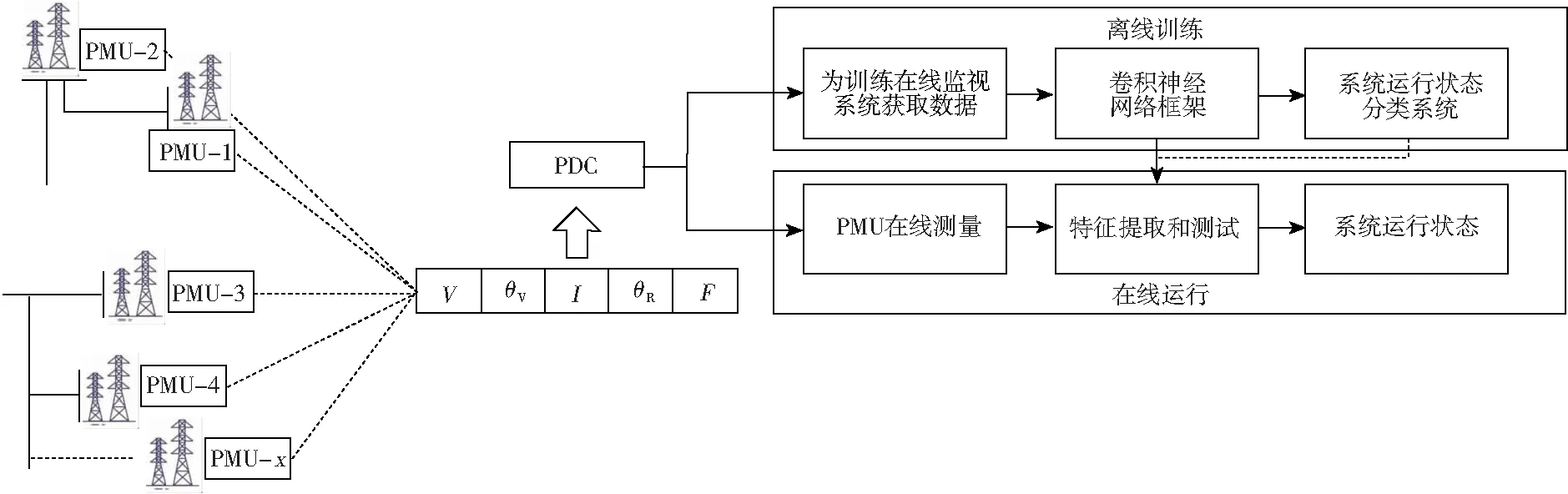
图1 监视框架

2.1 训练数据的获取

用于训练模型的参数是电流和电压幅值、转子角、电压角和系统频率[16-17]。在实际应用场景中，训练数据是从部署于所有发电机组母线上的PMU采集的。在本研究中，训练数据是通过PowerWorld软件环境中的IEEE 118仿真系统上的暂态稳定分析程序模拟得到的。IEEE 118仿真系统包括118条母线、54个发电机组、99个负载点和177条传输线。在仿真程序中，针对各种类型的故障(在总线长度的25%、50%和75%的3个不同位置，每条母线和每条传输线上的三相平衡故障)进行模拟。

每个故障事件持续20 s，整个仿真过程中的时间步长为0.02 s，因此每个故障仿真使用1 000个时间戳记录。对于每种故障情况，都会在t=1 s时模拟故障开始，并在8个周期(即0.133 3 s)内实现故障仿真，然后将其清除。在9个不同的负载级别(100%、97%、98%、99%、101%、102%、103%、104%和105%额定负载)下对母线故障和传输线故障进行仿真。

2.2 数据预处理

为了实时对发电机组暂态稳定性进行监视，需要在几个时间步长上连续分析电力系统参数。在连续t个时间戳组成的滑动窗口中观察所有参数。在每个采样时间点，滑动窗口由t-1个历史测量记录和1个当前测量记录组成。将观察到的原始数据排列并转换为由时间戳、生成器编号和参数组成的三维矩阵，如图2所示。然后按照时间先后为每个时间戳维度上的向量分配颜色，时间戳轴上最新向量分配最暗的颜色。发电机轴上有54个发电机组(G1—G54)，参数轴上共有5个参数。时间戳轴上有5个时间戳，这5个时间戳组成一个观察窗口，窗口的滑动步长为1个时间戳。

图2 三维数据矩阵

为每个数据样本创建三维矩阵的热图图像，即将每个样本的数据矩阵呈现为大小为T*N*P的图像。其中，T为观察窗口的长度；N为发电机组数量；P为参数数量。对于任何特定故障场景，其矩阵热图的大小都是恒定的，均为5*54*5。通过在参数轴上堆叠所有5个时间戳，将3D数据重新排列为2D矩阵形式(54 * 25)，可以得到如图3所示的母线故障情况下从三维数据矩阵提取的二维特征热图。

图3 二维特征热图

2.3 功角估算

除了直接从PMU单元获得的测量值之外，功角(转子角)也是在数据矩阵中使用的参数，该参数不能直接从PMU获得，需要通过参数计算得出[18]。研究采用以下方法对暂态条件下的功角进行估算[19]。

发电机电磁转矩可表示为：

Te=(Ld-Lq)idiq+kMFiFiq+(kMDiqiD-kMQidiQ)

(6)

发电机的转子运动方程为：

(7)

式中，Tm、Te、Ta分别为发电机的机械转矩、电磁转矩和加速转矩；k=3/2；Ld和Lq分别为定子的交轴和直轴电感；id、iq、iD、iQ和iF分别为各个交轴和直轴绕组中的电流；MD、MF和MQ分别为定子和磁场、定子和q轴、定子和d轴的最大互感；ω和ωs分别为转子角速度和同步角速度。

第n个时间窗口的转子扭矩为：

Ta(n)=Tm-Te(n)

(8)

将式(8)代入式(7)并将其积分，可得转子角速度为：

(9)

对转子速度积分可得出功角：

(10)

2.4 暂态稳定指数

研究使用暂态稳定指数来量化评估发电机组的暂态稳定性。如果发生故障并在8个周期(t=1.133 3 s)之后就将其清除，则可以通过暂态稳定指数来确定故障场景下的系统状态，其定义为：

溴芬酸钠滴眼液治疗眼部炎症的卫生技术评估…………………………………………………… 周鹏翔等（18）：2544

(11)

式中，Δδmax为故障后任意2台发电机之间最大转子角度差。

根据η值可将系统状态分类为稳定或不稳定状态。如果η>0，则系统状态是稳定的；否则该系统将被标记为不稳定。如果一个情况被分类为不稳定情况，并且某些发电机与其余发电机的角度差大于360°，则该组发电机被分类为处于不稳定状态发电机组。

由表1可知，发电机组运行状态分为6种不同的类别。

表1 发电机组运行状态标签

基于系统中发生故障事件的不同来区分系统操作状态。①第1类：所有观察到的数据矩阵都属于故障前的时间；②第2类：数据矩阵覆盖了故障发生时间点时间戳；③第3类：数据矩阵准确覆盖了故障发生和故障清除之间的时间戳；④第4类：数据矩阵中包括故障清除时间点的时间戳；⑤第5类：数据矩阵所包含数据均处于故障清除之后的阶段，都是稳定运行状态；⑥第6类：所有数据矩阵所包含数据处于故障清除之后的期间，包含不稳定状态期间的时间戳以及此后的所有时间戳。一组数据矩阵都与一组发电机机组关联。

训练数据是根据2.1节所述方法生成的，并根据表1进行分类和标记，然后将已标记数据用于训练带预测池化层的改进卷积神经网络框架。

2.5 带预测池化层的卷积神经网络

带预测池化层的卷积神经网络结构如图4所示。首先，基于二值化赋范梯度(BING)特征将输入图像切割为多个尺寸较小候选对象图片，选定的候选对象图片被馈送到2个卷积层中压缩为特征图。提取特征后，卷积神经网络被分为2个不同的分支。上分支为分类器1，用作对发电机组运行状态进行多标签分类。下分支为分类器2，该分类器用于识别发电机组是否处于不稳定状态。在分类器1中，将提取的特征馈送到Relu和完全连接的层中，然后使用softmax来提供输出。对于分类器2，提取的特征用作共享CNN的输入，并将单个预测得分与最大合并操作融合在一起。与分类器1不同，分类器2使用sigmoid激活函数。为了整合2个分支，2个分类器中的误差会在训练过程中一起传播回去。

图4 具有预测池化层的卷积神经网络结构

3 仿真实验

仿真实验将IEEE 118总线测试系统用作测试系统。实验中共模拟了5 652个在不同负载水平下的不同类型的故障。仿真数据集随机分为训练集和验证集。数据集中属于第5类状态的时间窗口的数据样本数量比其他类别大得多，而第2类、第3类和第4类数据样本的数量相对较少。为了平衡训练数据，使用下采样算法处理训练数据集，使得各类别数据的比例大致相等[20]。在采样期间，每个样本仅采样一次，并且训练和验证数据集是互斥的。

CNN算法的实现是在Tensorflow 1.14.0中通过NVIDIA GeForce RTX、64 GB GPU(CUDA 10.0)硬件支持下实现的。卷积神经网络使用Adam Optimizer进行训练，批处理大小为64。通过PowerWorld Simulator中的模拟生成的PMU读数的数据矩阵用作训练卷积神经网络的输入。输入数据矩阵的大小为5*54*5，等效热图大小为54*25。该热图尺寸与内核大小相近，目的是减少内核的计算负荷。

在本研究的在线监控系统中，与模型的准确性一样重要的一个关键因素是在2个分类器中计算输出所花费的时间。给定样本窗口的最终输出所需的时间应非常短，这样该系统才具备在线运行的可能性。

在2个模型架上进行训练效率和计算效率的对比实验。第1个模型是卷积神经网络框架(CNN)，第2个模型是带预测池化层的卷积神经网络框架(CNN-HCP)。实验的目标是对发电机组的运行状态进行分类和识别。实验得出的训练时间和在线监视时间如图5所示。由图5可知，2个框架最终输出的计算时间分别为4.94 μs和9.2 μs。尽管所提出的CNN-HCP框架在效率计算方面较慢，但是其计算效率仍然足够满足在线监视的需求。

图5 两种分类器的训练时间和测试时间对比

计算精度的仿真实验结果如图6的混淆矩阵所示。在该实验中，对每个类别分别抽取3 000个样本用于测试。图6中真实类别坐标轴代表测试数据的真实类别，预测类别坐标轴代表CNN-HCP模型的分类结果。由图6可知，各个类别的分类准确率均在90%以上。

图6 测试结果的混淆矩阵

在不同负载条件下对本文所提出的框架进行测试，并与CNN模型的测试结果进行对比。测试结果如图7所示。

图7 在不同负载条件下的分类准确性

由图7可知，与未使用预测池化层进行多标签分类的CNN模型相比，所提出的CNN-HCP框架在所有条件下的性能均更加优异。在额定负载条件下对模型进行训练时，将在训练数据集中模拟总数为628的包含3个位置的不同类型故障。在变化的负载条件(102%和103%额定负载)下，总共模拟了2 512个故障以进行模型训练。在2个负载条件下，从2个框架获得的分类器1的结果都显示出相似的准确率，但是本文所提出的框架的分类器2的准确率明显更高，这证明了所提出的框架在检测电力系统中的不稳定发电机组时具有更优异的鲁棒性。

4 结语

本文提出一种基于改进卷积神经网络实现发电机组运行状态在线识别的深度学习框架。所提出的框架对部署在发电机组母线上PMU的相量测量值进行特征提取，然后通过所提取特征对发电机组运行状态进行分类。由于数据集中可能存在不同类别标签的数据，首先，通过数据预处理将包含机组序号、时间戳和观测参数的三维数据矩阵转化为二维图像；然后，使用预测池化层依据预测特征对图像进行分割；最后，使用卷积神经网络对图像进行分类和识别。在不同负载条件下的仿真测试结果表明，建议的框架在可接受的计算效率下具有较高的准确性，适用于发电机组暂态稳定性的在线监测。