BSM1基准仿真数学模型在污水监测中的可行性分析

袁睿泽

(陕西国防工业职业技术学院，陕西 西安 710300)

污水监测指的是利用先进的科学技术，对环境或者水资源当中的污染因素进行观察、监控、测定，并以现代化手段深入分析监测结果，进而评价环境或水体质量，记录环境与水体质量长期以来的变化情况，为相关的改进或预防措施提供数据依据。在我国城镇化建设水平不断提高的大背景下，城镇地区常住人口数量逐年增加，污水污染由原先的农村分散式污染转变成城镇集中式污染，一定程度上加大了污水处理的难度[1-3]。经过多年来的研发与技术积累，我国在监测技术方面取得了长足的进步，针对不同污染物质的传感器设备开始应用于污水监测中，尤其是在5G技术开始投入规模化使用的情况下，污水数据的采集也更加便利，污水数据资源更加丰富，同时也对污水处理过程控制提出了更高的要求。相比于其他化工技术来说，污水处理系统普遍存在耦合性、滞后性、非线性等方面的特点，难以精准控制各项污水处理指标。因此，需要通过特定的数学模型对污水处理过程中各项参数的变化情况加以描述，进而持续调整污水处理方案[4-6]。2018年，欧盟科学技术与合作组织与国际水质协会开展合作并开发了“1号基准仿真模型”BSM1，该模型逐渐被世界各国应用于污水处理厂的长期的动态特性。研究将针对污水处理监测的一般需求建立基于BSM1仿真平台的数学模型，并对该模型在污水监测工作中的可行性进行分析[7-8]。

1 BSM1基准仿真模型概述

BSM1基准仿真模型以A2O工艺流程为基础，由活性污泥法1号模型所构成，用于描述污水处理过程的沉淀反应和生化反应，基本结构如图1所示。该模型沉淀共有10层。Z代表组分浓度、Q代表流量[9-10]。

图1 BSM1结构

依照污水处理生物脱氮的基本原理，整个生化处理流程的核心是硝化反应和消化反应，其中最重要的变量为硝态氮浓度。为了合理控制回流液中溶解氧含量，避免破坏前端缺氧池缺氧环境，该系统需要严格控制5号池中的溶解氧浓度[11-12]。由此可知，BSM1控制回路的基本原理在于通过控制氧传递系数来控制2号池的硝态氮浓度和5号池的溶解氧浓度。

BSM1基准仿真模型能够从动力学、化学、物理学等多个角度反映污水处理的脱氮过程，基于A2O工艺流程交换反应信息，对13种组分的反应过程加以描述，具体组分见表1。其中，X代表颗粒性组分，S代表可溶性组分[13]。

表1 ASM1中所有组分

在BSM1基准仿真模型中，污水的生物处理过程总共包括8个过程，具体内容如下。

(1)异养微生物的好氧生长。当异养菌处于氧容量充分环境时将通过易生物降解有机物促进生产，生长速率计算方法为：

(1)

(2)异养微生物的缺氧生长。当异养菌处于缺氧环境时将通过硝态氮和易生物降解有机物促进生长，生长速率计算方法为：

(2)

(3)自养微生物的好氧生长。当自养菌处于氧容量充分环境时将通过氨氮促进生长，生长速率计算方法为：

(3)

(4)异养微生物的衰减。本次研究默认微生物在任意环境均有相同的死亡速率，并逐渐转化为易溶生物可降解有机氮、生物衰减产生的颗粒产物、慢性可生物降解有机物，则异养微生物的衰减速率计算方法为：

ρ4=bHXBH

(4)

(5)自养微生物的衰减。自养微生物的衰减过程可以参照异养微生物衰减进行描述，衰减速率计算方法为：

ρ5=bAXBA

(5)

(6)易溶生物可降解有机氮的氨化。污水中的微生物在逐渐死亡的同时，易溶生物可降解有机氮也会随之发生氨化反应，氨化速率的计算方法为：

ρ6=kaSNDXBH

(6)

(7)缓慢生物降解有机物的水解。经过水解转化后的慢性可生物降解有机物会生产能够被微生物快速降解的有机物，进而促进微生物的生产，水解速率的计算方法为：

(7)

(8)缓慢生物降解有机氮的水解。经过水解后的颗粒性生物可降解有机氮会产生能够被微生物快速降解的有机氮，其水解速率的计算方法为：

(8)

以上8个反应速率计算方法中所包含的动力学参数见表2。根据各项反应速率计算方法可知，在有机底物浓度较低的情况下，反应速率会随着有机底物浓度的增加而增加，在反应速率达到最高的情况下，反应速率并不会因有机底物浓度的提升而增加。

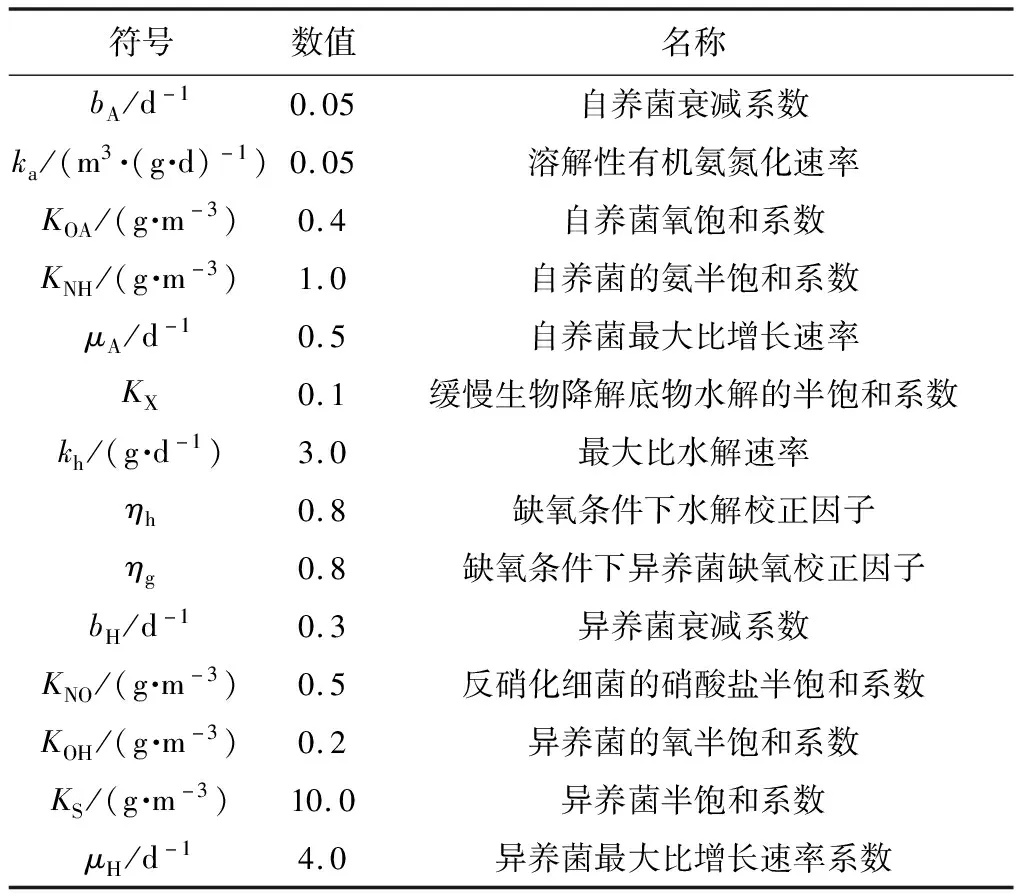
表2 ASM1中的动力学参数

在发生生物反应的过程中，各组分的反应随之发生，并且由一种或几种微生物的反应所构成。反应速率的计算方法：

(9)

不同组分反应速率计算方法为：

r1=0

(10)

(11)

r3=0

(12)

r4=(1-fp)ρ4+ρ4(1-fp)ρ5-ρ7

(13)

r5=ρ1+ρ2-ρ4

(14)

r6=ρ3-ρ5

(15)

r7=fpρ4+fpρ5

(16)

(17)

(18)

(19)

r11=-ρ6+ρ8

(20)

r12=(iXB-fpiXP)ρ4+(iXB-fpiXP)ρ5-ρ8

(21)

(22)

以上公式中所包含的化学计量参数见表3。

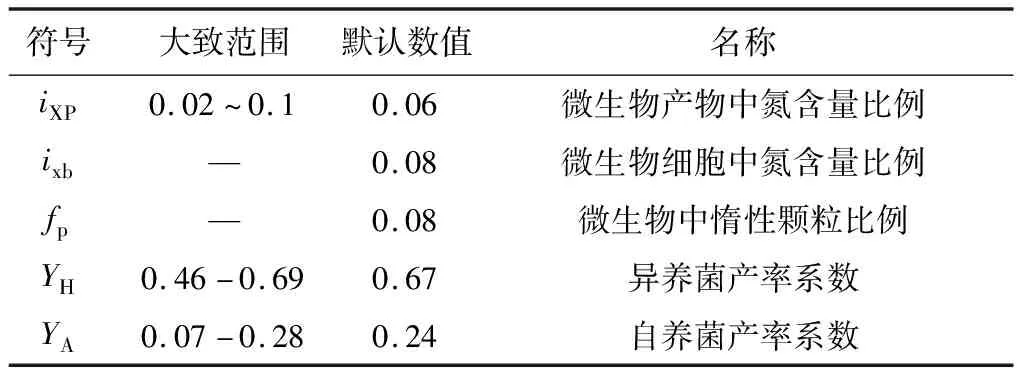
表3 ASM1中的化学计量参数X

基于物料守恒原则，各生化反应池内的组分之间必然存在一定的对应关系，设BSM1结构图(图1)中的5个生化池分别为k1、k2、k3、k4、k5，各生化池的体积为V1、V2、V3、V4、V5，则有如下所示的生化池物料平衡方程：

(23)

(24)

式(23)默认同一反应池内进水流量与出水流量相等且同步发生，并将k号池中13种组分反应速率的组合向量记为rk；式(24)中的进水流量等于首端入水、外汇流量和内回流量之和。

2 SIMULINK模型搭建

研究通过SIMULINK平台来搭建基于BSM1的生化池反应模型，进而对生化反应前后各组分的变化状况进行模拟。该模型的输出变量和状态变量同为14个，输出变量包括水流量和13种组分，状态变量包括氧传递系数和13组分，总计输入15个(氧传递系数、水流量和13种组分)，以5号反应池为例，该生化池反应模型如图2所示。

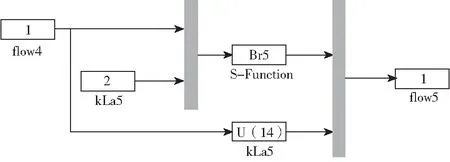
图2 单个反应生化池反应模型

图2中flow为水流信息，该模型的输入为由氧传递系数以外的其他输入变量所组成的列向量，由于反应池的排水流量等于入水流量，所以输入、输出流量数据也可以直接连接。设5号ASM1数学模型为Br5，以微分方程(23)为例，该程序应当综合13个微分方程对各组分的变化情况进行计算。由于各反应池均有相同的反应流程，并且全部遵循ASM1数学模型的动作原理，因此各反应池也都可以采用相同的建模方法。各组分状态数值更新流程如图3所示。

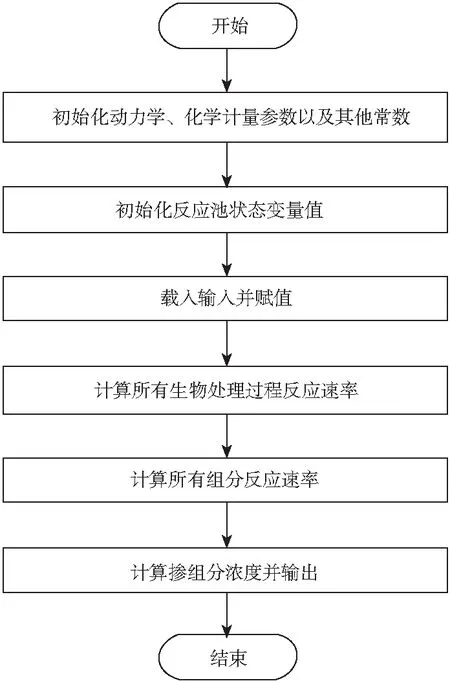
图3 生化池状态变量更新流程

3 BSM1基准仿真平台测试

为了保证模型仿真的真实性，本次研究在污水处理厂采集了14 d的真实数据，具体包括暴雨、雨、晴天3种天气下的工况数据。晴天入水流量变化如图4所示，晴天入水可溶性组分浓度变化如图5所示，晴天入水难溶性组分浓度变化如图6所示，雨天入水流量变化如图7所示。

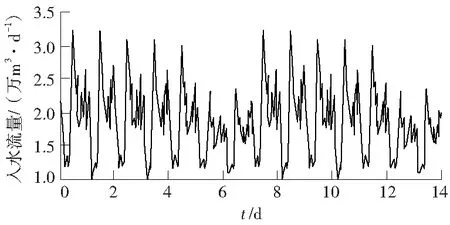
图4 晴天入水流量变化

图5 晴天入水可溶性组分浓度变化

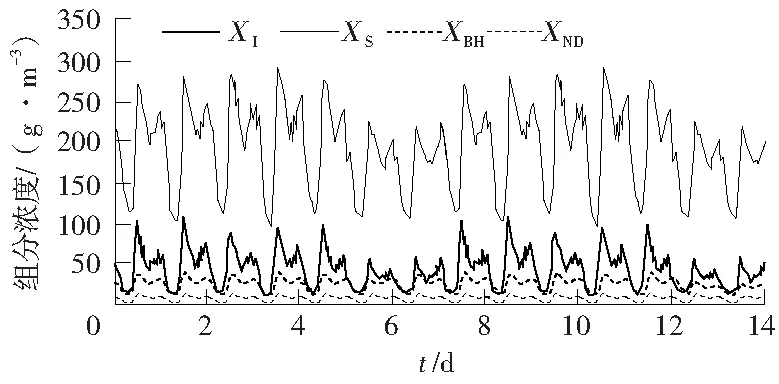
图6 晴天入水难溶性组分浓度变化

经统计分析可知，污水处理系统的入水情况每7 d为一个周期，与城市居民的活动规律相符。根据图4可知，周一至周四入水流量较小，周五、周六、周日污水处理工作量较少；根据图5和图6可知，颗粒悬浮物和氨氮排放量明显超标，在同一个周期内，入水流量的增加会带动入水组分的提升，此时流量和浓度未发生明显波动；根据图7可知，由于第8—11天受降雨影响，入水流量在当日突增。

图7 雨天入水流量变化

研究为了对基于BSM1的生化池反应模型的正确性进行验证，对该模型实施为期100 d的开环仿真实验。BSM1开环仿真模型如图8所示。其稳态输入数据为晴天入水数据的平均值，设定5号池氧传递系数84 m3/d、内回流量55 336 m3/d、污泥排量385 m3/d、污泥回流量18 446 m3/d。

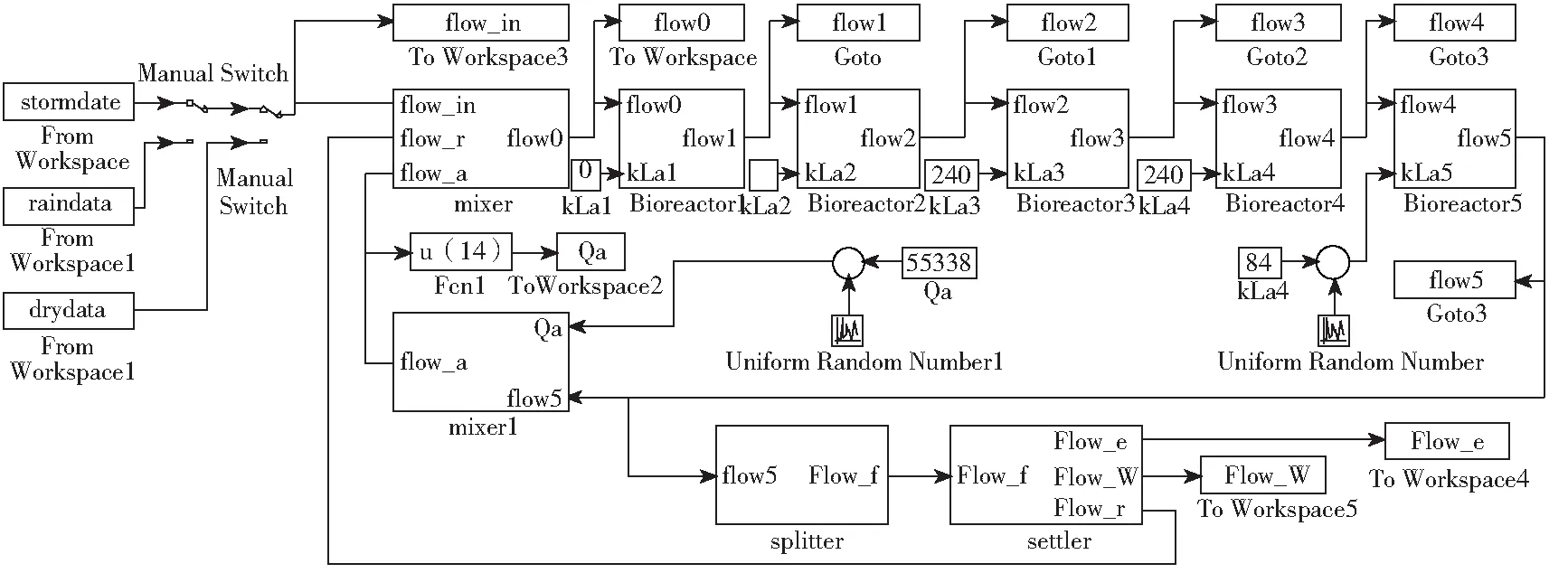
图8 BSM1开环仿真模型

经过计算机处理后得到的运行结果见表4。根据国际水协会提供的参考值与仿真对比稳态出水数据可知，基于BSM1的生化池反应模型具有充分的可行性，所得到的仿真值与参考值十分接近，能够应用于一般的污水监测工作，该组数据也包括了入水流量以及13种组分，基本可以满足污水处理工作实践可能遇到的所有情况。

表4 稳态出水数据

4 结语

本次研究详细介绍了BSM1基准仿真数学模型在污水监测中的工作原理与应用策略，阐述了该模型下污水的生物处理过程与各组分反应速率的计算方法，提出了基于BSM1的生化池反应模型并通过仿真模拟的方式对该模型的可行性进行了验证。经实验研究发现，基于BSM1的生化池反应模型的仿真结果与实际参考值十分接近，将该模型应用于污水监测具有较为充分的可行性。