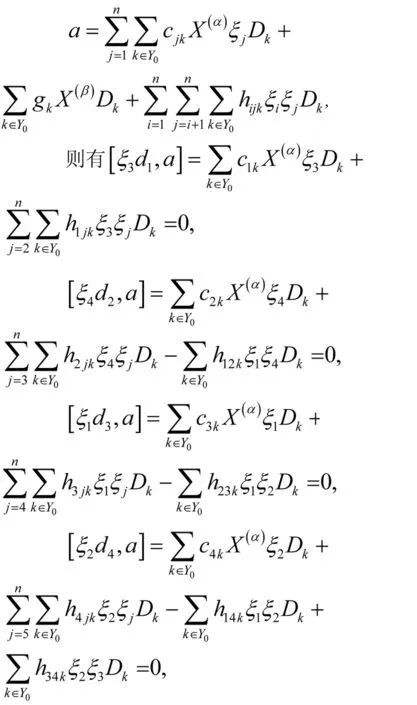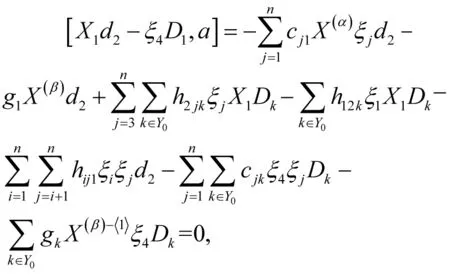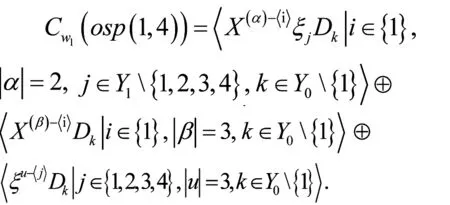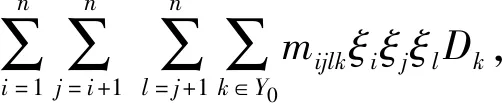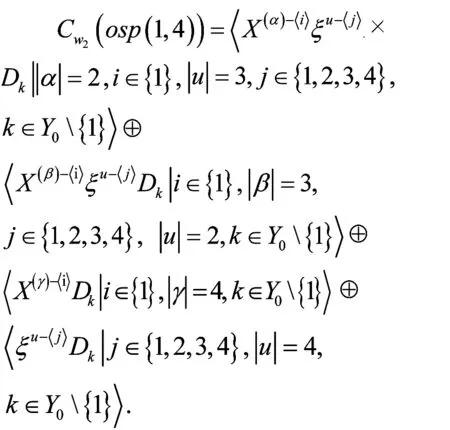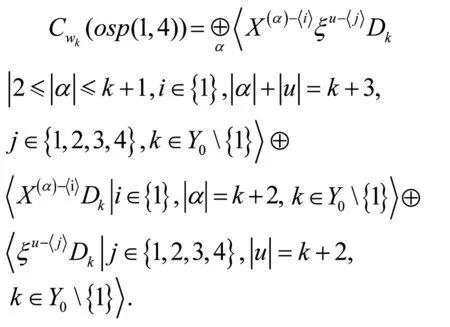素特征域上osp(1,4)在广义Witt李超代数中的中心化子*

张馨悦，张雪天，刘 娜，郑克礼

(东北林业大学)

0 引言

1933年，H.Weyl第一次用“李代数”代替了“无穷小群”，自此李代数开始被更多的人所关注. 经过历代数学家们的努力，目前李超代数的相关理论问题已经基本解决[1-2]，然而对于李超代数的相关问题的研究仍然不完善，还有许多问题亟待解决. 由于李超代数在物理、数学等方面的实际应用[3]，近年来对于李超代数的探究也越来越积极. 中心化子是一个子代数，其概念起源于抽象代数中群结构的研究[4]. 由于中心化子对于研究李超代数结构具有重要意义，因此对于中心化子的研究是不容忽视的. 文献[5]用矩阵完全表示出了系数在模李超代数W(m,3,1)上的gl(2,F)的一维上同调. 文献[6]刻画了因子von Neumann代数以及三角代数上非线性Lie中心化子.文献[7]研究了任意域上自同态的中心化子并计算了它的维数，同时得到了相应的广义Weyr标准形及其中心化子的结构.

该文以素特征域上一类一般线性李超代数的子代数osp(1,4)为例，研究其在广义Witt型李超代数上的中心化子. 该文的原始思想来源于文献[8-10]，并利用广义Witt李超代数的直和分解和求解线性方程组的方法分别计算了在素特征域上的Cw(osp(1,4))和Cω(osp(1,4)). 最后得到了osp(1,4)在广义Witt型李超代数中的中心化子结构. 该文所涉及代数的基域都默认为特征大于 2的代数闭域.

1 预备知识

设W为广义Witt型模李超代数[2]，且其有如下结构：

W=w⊕ω.

其中：

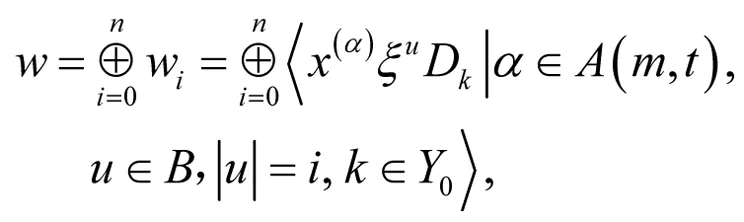
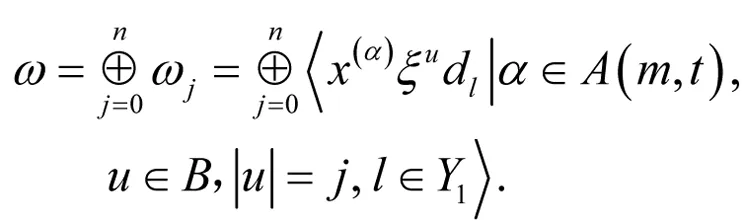
易知{X1D1,X1d1,X1d2,X1d3,X1d4,ξ1D1,ξ1d1,ξ1d2,ξ1d3,ξ1d4，ξ2D1,ξ2d1,ξ2d2,ξ2d3,ξ2d4,ξ3D1,ξ3d1,ξ3d2,ξ3d3,ξ3d4,ξ4D1,ξ4d1,ξ4d2,ξ4d3,ξ4d4} 是W中的一个子集，它同构于gl(1,4)的一组基.

定义(2m+2n+1)×(2m+2n+1)阶矩阵，

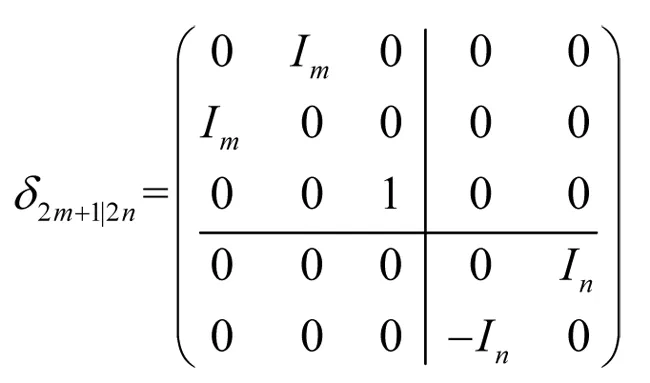
其中Im是m×m阶单位矩阵，In是n×n阶单位矩阵. 令δ2m|2n表示从中删除第2m+1行与第2m+1列所得到的(2m+2n)×(2m+2n)阶矩阵，那么有osp(1，4)={g∈gl(1,4)|gstδ1|4+δ1|4g=0}其中gst表示g的超转置，则osp(1,4)可由如下矩阵表示

可以得到

{e12+e41,e13+e51,e14-e21,e15-e31,e22-e44,e23-e54,e32-e45,e33-e55,e25+e34,e43+e52,e24,e35,e42,e53}为osp(1,4)的一组基，其中eij是(i,j)位置为1，其他位置为0的矩阵. 则显然有{X1d1+ξ3D1,X1d2+ξ4D1,X1d3-ξ1D1,X1d4-ξ2D1,ξ1d1-ξ3d3,ξ1d2-ξ4d3,ξ2d1-ξ3d4,ξ2d2-ξ4d4,ξ1d4+ξ2d3,ξ3d2+ξ4d1,ξ1d3,ξ2d4,ξ3d1,ξ4d2}是同构于osp(1,4)这组基的一个W的子集. 因此，为了确定素特征域上的Cw(osp(1,4))，只需对所有的i=1,2,…,n考虑Cwi(osp(1,4))和Cωi(osp(1,4))即可.

2 素特征域上的Cw(osp(1,4))

命题1Cw0(osp(1,4))=〈X(α)-〈i〉Dk|i∈{1},|α|=2,k∈Y0{1}〉⊕〈ξjDk|j∈Y1{1,2,3,4},k∈Y0{1}〉.

证明由定义有w0=〈x(α)ξuDk||α|+|u|=1,k∈Y0〉，可将其分为ξjDk和X(α)Dk，|α|=1,|u|=0. 令[osp(1,4),a]=0，

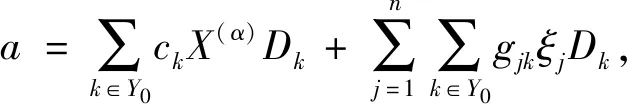
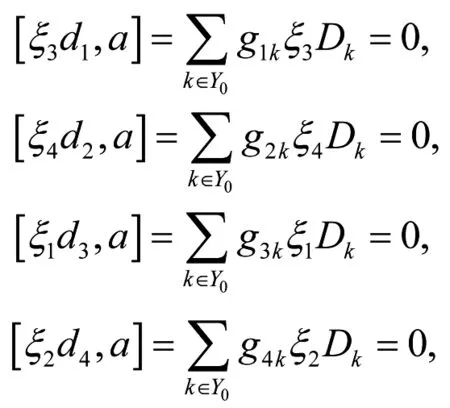
由于D1,D2,…,Dm线性无关，则由上式可得

g1k=g2k=g3k=g4k=0.又有

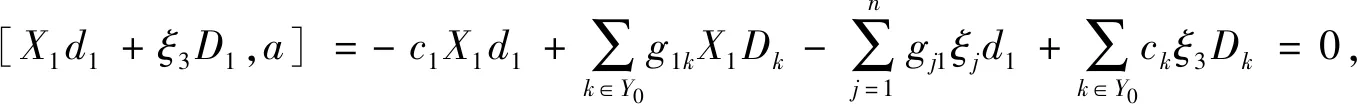
综上所述，有Cw0(osp(1,4))=〈X(α)-〈i〉Dk|i∈{1},|α|=2,k∈Y0{1}〉⊕〈ξjDk|j∈Y1{1,2,3,4},k∈Y0{1}〉.

命题2

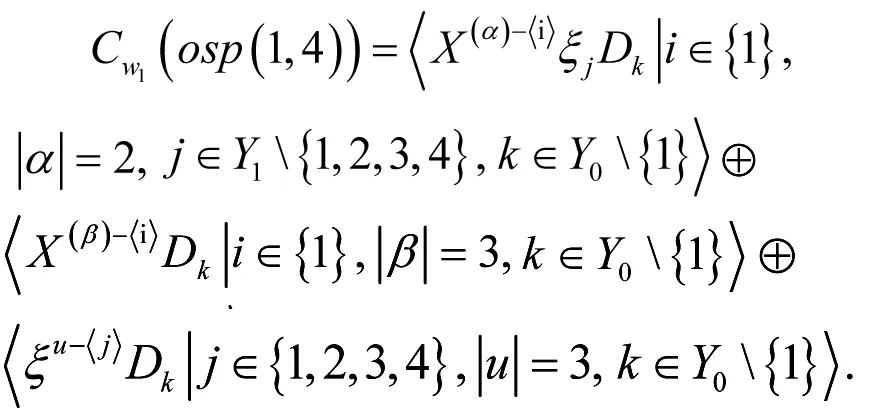
证明由于w1=〈X(α)ξuDk||α|+|u|=2,k∈Y0〉，可将其分为ξiξjDk,X(α)ξjDk和X(β)Dk三种情况，其中|α|=1,|β|=2.

(1)当X(α)ξuDk的X(α)为X1，X(β)中含有X1时，对于ξiξjDk(i

由于D1,D2,…,Dm线性无关，则由上式知c1k=c2k=c3k=0,h1jk=h2jk=h3jk=h4jk=0.

易知hij1=0,gk=0,cjk=0，此时结果为

〈ξu-〈j〉Dk|j∈{1,2,3,4},|u|=3,k∈Y0{1}〉.

(2)当X(α)ξjDk中X(α)不为X1，并且同时满足X(β)中不含有X1,k∈Y0{1}时，则有[osp(1,4),a]=0，此时结果有

〈X(α)-〈i〉ξjDk|i∈{1},|α|=2,j∈Y1{1,2,3,4},k∈Y0{1}〉⊕〈X(β)-〈i〉Dk|

i∈{1},|β|=3,k∈Y0{1}〉.

综上所述，可以得到

命题3

证明由w2=〈X(α)ξuDk||α|+|u|=3,k∈Y0〉可知，可将其分为ξiξjξlDk,X(α)ξiξjDk,X(β)ξjDk,X(γ)Dk四种情况，其中|α|=1,|β|=2,|γ|=3.

(1)若X(α),X(β),X(γ)中含有X1时，对于ξiξjξlDk,i

由[ξ3d1,a]=0,[ξ4d2,a]=0,[ξ1d3,a]=0,[ξ2d4,a]=0可知c1k=c2k=c3k=c4k=0,

mijlk=0,hijk=0，其中i=1,2,3,4. 由[X1d1-ξ3D1,a]=0可知cjk=hijk=gk=0. 此时结果有〈ξu-〈j〉Dk|j∈{1,2,3,4},{u}=4,k∈Y0{1}〉.

(2)若X(α)、X(β)、X(γ)中不含有X1，则[osp(1,4),a]=0.

此时结果为〈X(α)-〈i〉ξu-〈j〉Dk||α|=2,

i∈{1},|u|=3,j∈{1,2,3,4},k∈Y0{1}〉⊕〈X(β)-〈i〉ξu-〈j〉Dk|i∈{1},|β|=3,j∈{1,2,3,4},|u|=2,k∈Y0{1}〉⊕

〈X(γ)-〈i〉Dk|i∈{1},|γ|=4,k∈Y0{1}〉.

综上所述，有

推论1 对于wk(k≥1)而言，结果应有k+2项直和. 即

由命题1～3以及推论1即可得到以下定理：

定理1Cw(osp(1,4))=Cw0(osp(1,4))⊕Cwk(osp(1,4))，其中1≤k≤n.

运用以上命题的相同证法可得：

命题4Cω0(osp(1,4))=〈X(α)-〈i〉dk|

i∈{1},|α|=2,k∈Y1{1,2,3,4}〉⊕〈ξjdk|j∈Y1{1,2,3,4},k∈Y1{1,2,3,4}〉.

命题5Cω1(osp(1,4))=〈X(α)-〈i〉ξu-〈j〉×

dk|i∈{1},|α|=2,j∈{1,2,3,4},k∈Y1{1,2,3,4}〉⊕〈X(β)-〈i〉dk|i∈{1},|β|=3,k∈Y1{1,2,3,4}〉⊕〈ξu-〈j〉dk|j∈{1,2,3,4},|u|=3,k∈Y1{1,2,3,4}〉.

命题6Cω2(osp(1,4))=〈X(α)-〈i〉ξu-〈j〉×

dk||α|=2,i∈{1},|u|=3,j∈{1,2,3,4},k∈Y1{1,2,3,4}〉⊕〈X(β)-〈i〉ξu-〈j〉dk|i∈{1},|β|=3,j∈{1,2,3,4},|u|=2,k∈Y1{1,2,3,4}〉⊕〈X(γ)-〈i〉dk|i∈{1},

|γ|=4,k∈Y1{1,2,3,4}〉⊕〈ξu-〈j〉dk×

|j∈{1,2,3,4},|u|=4,k∈Y1{1,2,3,4}〉.

推论2 对于ωk(k≥1)而言，结果应有

k+2项直和. 即

由命题4～6以及推论2即可得到以下定理：

定理2Cw(osp(1,4))=Cω0(osp(1,4))⊕Cωk(osp(1,4))，其中1≤k≤n.

由定理1和定理2可得以下定理：

定理3CW(osp(1,4))=Cw(osp(1,4))⊕Cwosp(1,4))=Cw0(osp(1,4))⊕Cω0(osp(1,4))⊕Cwk(osp(1,4))⊕Cωk(osp(1,4)),

其中1≤k≤n.