非线性反问题的elastic-net 正则化
王思雨,丁 亮
(东北林业大学)
0 引言
该文研究非线性不适定算子方程
F(x)=y
(1)


(2)
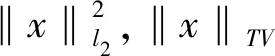

(3)

对于非线性不适定问题,elastic-net正则化在应用方面也有一定的研究.2010年,Umanità等人对elastic-net正则化解的渐进性质进行了严格的研究[10].2012年,Jin和Maass的研究集中在这类具有非线性算子泛函的正则化性质[11].2018年,Wang等人研究了用快速迭代阈值算法(FISTA)求解elastic-net正则化[12].证明基于EN的PC-EnKF与基于PC的迭代旋转方法相结合非常适合于高维非线性逆建模.2019年,Wang等学者考虑到l2-罚项总是使解过于光滑,l1-罚项总是使解过于稀疏的事实,将elastic-net正则化方法用于严重不适定非线性EIT反问题[13].
以上内容是elastic-net 正则化在非线性问题中的应用.目前,非线性反问题的elastic-net正则化理论还处于空白状态,在理论分析及数值方法上还有许多亟待解决的问题.故该文的主要目的是分析基于非线性不适定问题的elastic-net正则化解的存在性,稳定性和收敛性.特别是在适当的源条件下,建立正则化解的收敛速度.

1 Elastic-net正则化的性质

Rα,β(x)=αRη(x) ,
(4)
(5)
因此(3)可以转化为如下形式:
(6)


(7)
接下来证明正则化解的存在性、稳定性和收敛性.
定理1 假设非线性算子F:l2→Y是弱序列闭的,对所有α>0,(3)存在一个解.
证明由于Rα,β(x)≥0是适当的,因此存在一个最小值序列{xk},使得
(8)
由式(8)可知‖xk‖l1,‖xk‖l2和‖F(xk)‖是一致有界的.因此,存在一个子序列{xkj}和一个元素x*使得在l2空间中{xkj}弱收敛到x*.由于F是弱序列闭的,则F(xkj)→F(x*),弱下半连续的形式意味着

(9)
由于l1-范数及l2-范数是下半连续的,有x*∈l2且
(10)
由(8)、(9)及(10)可知x*是Φα,β(x)的一个最小值解.
接下来证明正则化解的稳定性.

证明xn的最小化性质意味着序列{‖F(xn)-yδ‖Y},{‖xn‖l1}和{‖xn‖l2}是一致有界的.特别地,存在一个{xn}的子序列,也表示为{xn}弱收敛到x*∈l2.则

因此,有
(11)


(12)
通过xn的极小化性质,即

(13)
因此,x*是Φα,β的一个最小值解.
2 收敛性和收敛速度
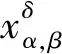
定理3 假设正则化参数α(δ)和β(δ)满足
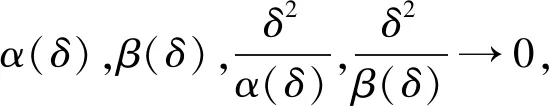
此外,存在常数η≥0,使得
(14)
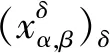

(15)

由三角不等式,得到

(16)


(17)

通过调用标准子序列参数,整个序列弱收敛.通过不等式(17)有
(18)
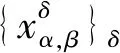
假设1 设xτ≠0是问题(1)的一个Rη-极小化解,并且是稀疏的,假设
(i)F连续Fréchet可导.
(ii)存在一个γ>0,x∈R(x)≤σ,R(xτ)<σ,使得
‖F′(x)-F′(xτ)‖L(X,Y)≤γ‖x-xτ‖.
(19)
(iii)存在一个ω∈Y,且使得
F′(xτ)*ω=ξ+ηxτ.
(20)
假设3.1(i)说明了解xτ的光滑性,假设3.1(ii)有两层意义,一个是F的非线性条件,另一个更重要的作用是估计
注由F的泰勒估计可知
(21)
因此,由三角不等式得
(22)
可以用来估计

和
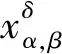
得到


化简得
由于ξ∈D(F′(xτ)*)是任意的,可以用源条件的方法选择,即F′(xτ)*ω=ξ+ηxτ,
化简得
ω>.
(23)
由(22)得
yδ‖Y+‖ω‖‖yδ-F(xτ)‖Y.

(24)
将(24)代入(23)中得
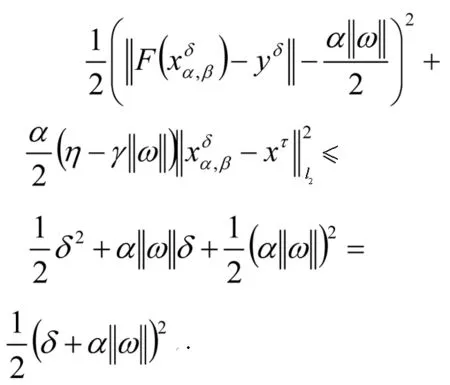
定理得证.
定理5 假设解xτ是稀疏的且满足源条件(20),非线性算子F满足有限维内射基性质.因此存在两个正常数C1和C2使得
Rη(x)-Rη(xτ)≥C1‖x-xτ‖l2-C2‖F(x)-F(xτ)‖ .
证明设ξ∈sign(xτ)满足源条件(20),用Ⅱ表示指标集
由源条件(20)得

‖ω‖‖F′(xτ)(x-xτ)‖≤
C‖ω‖‖F(xτ)-F(x)‖.
(25)




当C1=C+2η-1(1+C‖F′(x)‖)‖ω‖,C2=2η-1(1+C‖F′(xτ)‖) 时等式得证.
3 结 论
该文给出了非线性问题elastic-net正则化
的正则化性质的分析与证明,难点在于它的算子是非线性算子,有不止一个最小值,并且罚项为l1和l2两项.因此将elastic-net应用到非线性问题以后,可以从误差估计中得到好的正则化收敛速度和较小的误差估计,证明了elastic-net正则化结合了l1正则化和l2正则化的优点.

