基于支持向量数据-贝叶斯模型的冷水机组故障检测与诊断研究

刘伫熔，叶琳，丁之劼，茅一峰，李前舸，晋欣桥，杜志敏*

（1-上海交通大学制冷与低温工程研究所，上海 200240；2-中国船舶重工集团公司第七〇四研究所，上海 200031）

0 引言

空调系统故障检测与诊断方法，可以分为三类，分别是基于模型方法、基于规则方法和基于数据驱动方法[1-3]，精确的物理模型实际建模并应用难度较大[4-9]，基于规则方法需要精确匹配故障[10-11]，基于数据驱动的方法的可解释性较差，因此训练过程不可控[12-15]。

贝叶斯网络融合了基于数据驱动与基于规则的方法，其特点介于白箱模型与黑箱模型之间，可有效用于对冷水机组进行故障检测与诊断。对于冷水机组各部件的耦合情况，运行原理以及规律性信息不需要做到完全提取与充分训练。对于一个复杂的冷水机组，求解问题的过程中允许使用对系统进行简化近似的灰箱模型。在建立网络的过程中需要引入专家知识判定不同故障与事件之间的联系以确定网络结构。在求解条件概率时引入统计学中贝叶斯观点，将事件频率视为发生概率，相较于仅基于规则判定冷水机组是否存在故障，贝叶斯网络输出各个故障发生的概率，更为科学直观[16-17]。

但用于冷水机组故障诊断的贝叶斯网络属于离散型贝叶斯网络，故障的检测与故障的诊断同时进行。通常而言无法进行无故障情况的识别，当输出故障后验概率大于设定值时即同时完成故障的检测与诊断。而该种方法在概率特征空间里通过离散变量将其划分为不同的故障事件空间。而对于故障事件空间与无故障事件空间则没有进行划分，导致模型对于无故障情况的空间范围无法控制。如图1所示，无故障的特征空间划分是由故障一与故障二的特征空间划分确定的，随着划分平面的增多，无故障的特征空间也会随之改变。香港理工大学的赵阳等[18-19]通过在贝叶斯网络模型中确定人为规则进行无故障空间的划分，例如当所有贝叶斯网络中故障输出后验概率均小于0.6且前两位概率之差小于0.3时，认为此时系统未发生故障。

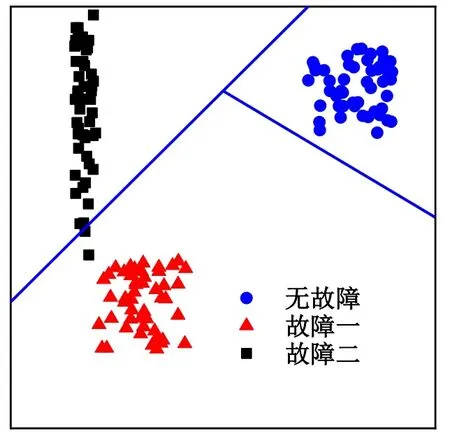
图1 非独立检测中事件空间划分

当发生诊断贝叶斯网络中未收录的故障时，模型中对应监测的运行参数可能对未知故障不敏感，导致症状无法捕捉。单独使用诊断贝叶斯网络进行此类样本的诊断会出现故障节点输出概率偏低，无法检测到故障，导致漏警情况。

基于以上原因，本文使用支持向量数据描述（Support Vector Data Description，SVDD）方法确定无故障的特征空间边界并进行故障的检测[20-21]。通过输入全部无故障样本，训练无故障情况的特征空间，从而弥补诊断贝叶斯网络训练过程中无故障边界无法确定的问题。当出现诊断贝叶斯网络输出故障概率偏低的情况，是否发生未知故障可由SVDD模型进行确定，减少了人为主观选定未知故障检测阈值对模型漏警或误警的影响。

1 支持向量数据描述（SVDD）方法

SVDD是一种用于离群点检测的算法，原理如图2所示，主要思想是根据所给特征在高维空间内最小化边界包裹全部正样，从而筛选样本分布的高密度区域与低密度区域。通过判断测试集与所确定边界的关系进行离群点的判定。

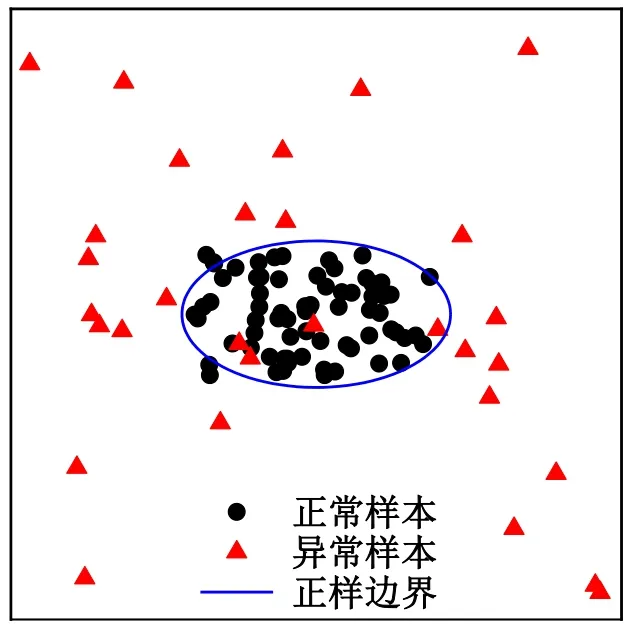
图2 支持向量数据描述原理

特征空间中分布在分割曲面上的样本即支持向量。训练过程中目标函数表示为：

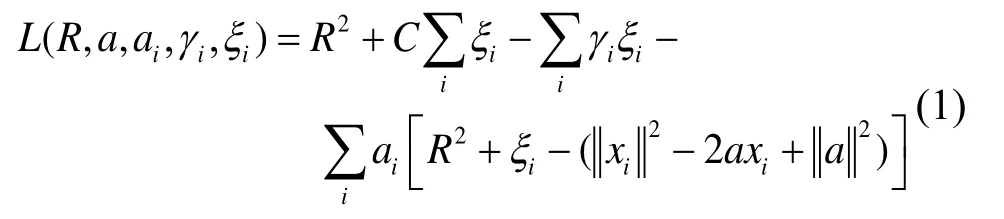
式中，a为高维超球球心；R为高维超球半径；xi为样本i；C为惩罚系数，控制训练松弛程度；αi，γi为拉格朗日乘子；ξi为样本i标签。

惩罚系数C决定了对于误分类样本的惩罚力度，C越大，对样本的聚集程度要求越高。C过小使模型在训练过程中误分样本过多而导致欠拟合，因而需要确定合适的惩罚系数C。另外，在使用SVDD方法训练无故障边界时，还需要确定高斯核的宽度参数γ。当集群点密集度较低时，过大的γ会让样本映射过分稀疏，导致训练边界欠拟合；而较小的γ导致较多样本被确定为支持向量。对于样本本身集群度较高的案例，过小的γ会使集群点难以分离。

Python中使用LibSVM模块进行SVDD训练时，惩罚系数C会根据所输入γ而主动寻优，因而只需确定超参数γ。使用模拟退火算法确定γ值，训练流程如图3所示。

图3 基于模拟退火的故障检测模型训练流程

2 诊断贝叶斯（DBN）模型

对于诊断贝叶斯网络（Diagnostic Bayesian Network，DBN）模型而言，需要确定的要素包括两部分，网络结构以及各个节点的条件概率表，模型构建流程如图4所示。经过实验与前期的数据处理，已经得到了稳态情况下的故障与无故障数据，首先需要确定网络的结构。冷水机组诊断贝叶斯网络中，各个故障节点为父节点，证据节点为子节点。本文通过热力学分析确定了对于不同故障敏感的运行参数，而规则表中故障与参数之间的每一条规则对应贝叶斯网络中的一条边。具体结构如图5所示，网络图中故障节点符号F与证据节点E。

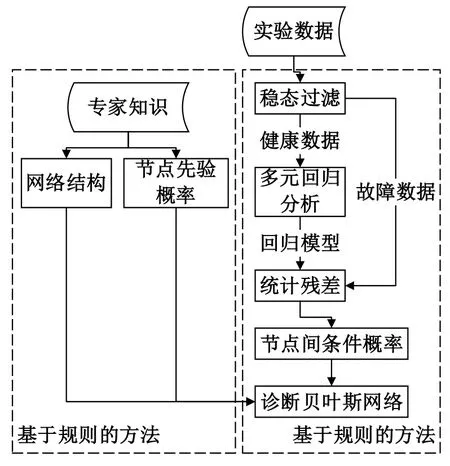
图4 贝叶斯网络诊断模型构建流程

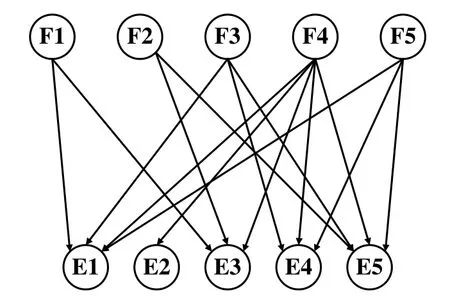
图5 诊断贝叶斯网络结构

在确定网络结构后，需要确定网络模型中的各项参数，包括不同故障的发生概率以及故障与对应症状之间的条件概率。对于故障节点的先验概率，已有的研究中针对这方面的成果较少，实际应用中考虑建模与采样时样本分布的一致性可以考虑使用不同故障的发生频率代替概率，而本文在验证模型效果时使用的测试集样本分布与实际分布有较大偏差，会降低贝叶斯网络的准确性，因而在验证模型效果时将全部故障的先验概率设置为0.5。

对于故障与症状之间的条件概率，本文对冷水机组进行了不同种类的故障诊断实验，根据故障发生时证据节点变量与正常值的偏离频率作为症状发生的条件概率。

3 SVDD-DBN模型

结合支持向量数据描述方法的诊断贝叶斯网络故障诊断流程如图6所示，其中诊断规则为当且仅当模型对于一个故障的输出后验概率大于60%。若所有故障概率均小于该阈值或多个概率大于该阈值，则判定不符合诊断规则。

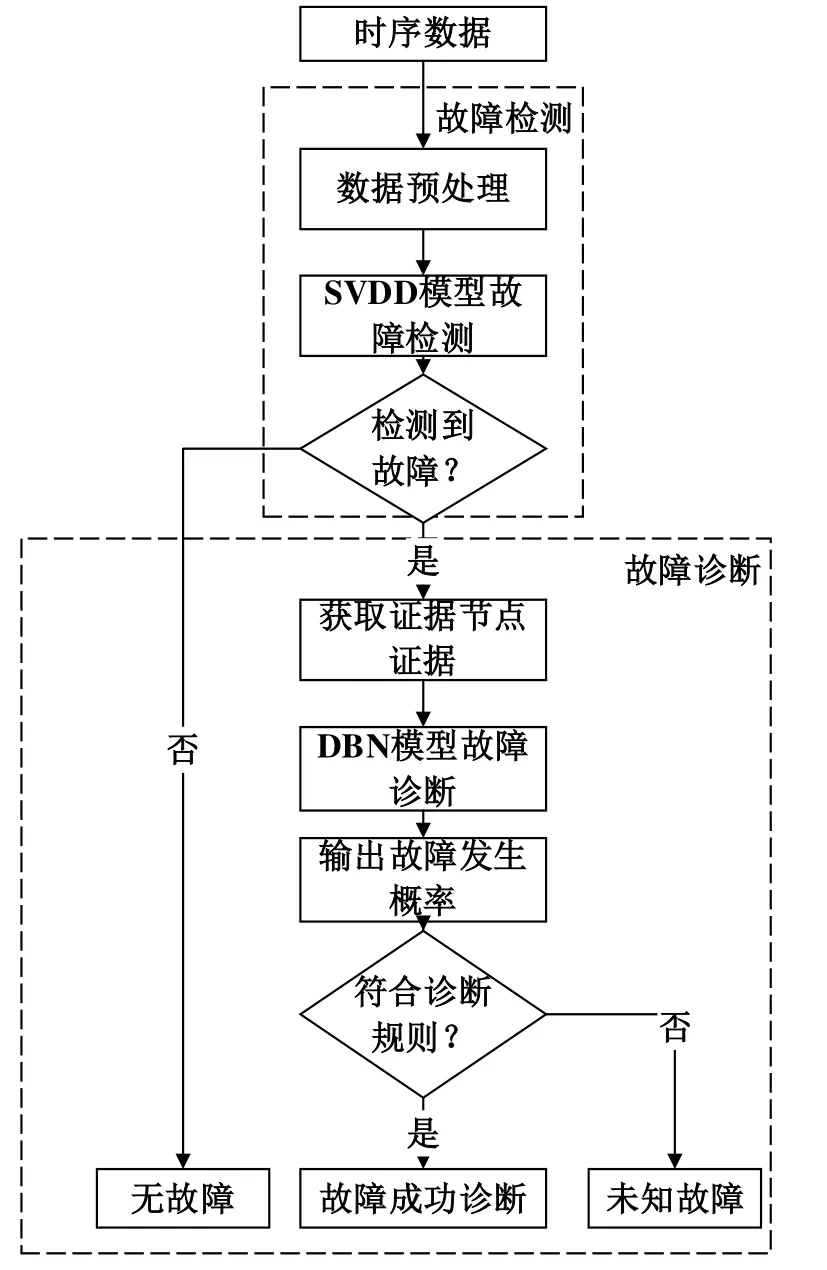
图6 SVDD-DBN诊断流程

通过将各类独立发生的故障数据输入到所建立的诊断贝叶斯网络中，通过对于诊断结果的定量分析，确定模型的诊断效果。

3.1 SVDD故障检测模型验证

当输入新样本时，模型使用训练的映射关系将样本映射至高维空间，判断样本在特征空间内与支持向量球面的距离。当距离大于0时表示样本位于无故障球空间内，为正常样本；当距离小于0时表示样本位于无故障球空间外，即检测到故障产生。

先使用70%的无故障数据训练得到无故障模型。将剩余的30%无故障工况数据与全部5种故障情况的故障水平数据合并作为测试集。模型在测试集上的分类错误率为6.4%，分类结果如图7所示。由图7可知，由于在模型训练过程中允许对于正样的适当误分类，模型在测试集中无故障样本也有少量误分的情况出现。而对于制冷剂充注量不足故障，实验中模拟故障水平分别为标定充注量的90%与80%；由于故障水平较低，因此对于系统的热力参数影响较小，同样出现少量误分类情况；而其余故障情况的检测率接近100%，即SVDD故障检测模型的误警率主要来源于以上两种情况。

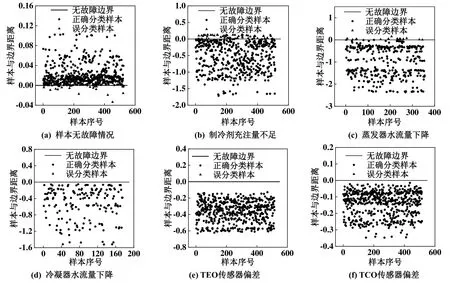
图7 SVDD模型测试集输出结果

3.2 SVDD-DBN故障检测模型验证

使用第2节所描述的实验数据对所建立的诊断贝叶斯网络模型进行验证。在所进行的实验中，测试冷水机组环境温度与真实天气条件下环境温度相同。分别从无故障数据，5种独立故障的数据中各抽取9组实验样本作为测试集输入到模型中。

为了使症状表现易于捕获，在选取测试集时从故障水平较高的实验数据中进行抽取，此外，由于诊断贝叶斯网络模型效果受无故障模型影响，该无故障模型预测准确度存在波动，因而在抽取同一故障的样本进行验证时选取天气条件相近的数据进行抽取。用于筛查机组稳态的时间窗长度选为60 s，对于一个给定的实验样本，仅当其无症状时间小于所选定无症状时间占比阈值时才记为对应症状发生。当设定置信度为97.7%时，模型诊断效果混淆矩阵如图8所示。混淆矩阵横轴表示模型诊断的输出结果，纵轴表示输入样本的真实情况。数值表示该种结果占样本比重。混淆矩阵中每一行之和可能出现不为1的情况，其原因在于根据所选用故障诊断规则，当且仅当单类故障发生概率大于60%，而当多种故障发生概率同时大于60%时，模型无法判断所发生的故障种类。

图8 置信度97.7%诊断结果（%）

当置信度为97.7%时，模型对于不同情况的诊断成功率相差较为悬殊，其中测试集中无故障情况，制冷剂充注量下降以及TCO传感器偏差的诊断成功率均达到100%。冷凝器水流量下降情况的9个样本中7个进行了成功诊断，达到了可接受的诊断成功率，但2个样本被误诊为制冷剂充注量下降。两种故障特征不同，从贝叶斯网络进行概率输出的角度考虑，理论上不应该出现该种误诊断，且调整模型置信度后，区间进一步放大。推测是由于阈值发生改变时，症状捕捉条件也随之发生改变，例如蒸发压力该症状在部分工况中未进行成功捕捉，导致输入模型的信息不完整，从而出现了误判，该原因尚有待进一步考证。此外，蒸发器水流量下降与TEO传感器偏差的故障诊断成功率不理想。由于两类故障均同时出现了较高的发生概率，而在本文建立诊断规则时，对诊断模型提出不同事件父节点不会同时发生的假设，因而现有模型无法进行成功故障分离，需要对模型进行进一步的优化。

4 结论

本文结合支持向量数据描述SVDD与诊断贝叶斯网络DBN两种方法，使用冷水机组不同故障情况下的数据作为测试集合进行测试，采用SVDDDBN模型进行故障检测与诊断，得出如下结论：

1）通过模拟退火算法优化支持向量数据描述模型可以进行故障检测，预先判断是否无故障，且效果较好；

2）对于模型中症状较为独立的故障，如制冷剂充注量下降，TCO传感器偏差；在实验症状表现不明显的情况下，由于其症状明显区别于其他故障，能获得较好的诊断结果，当取无故障区间为3倍标准差时，测试集正确率可达到100%；

3）对症状相似的故障，调节症状捕获的阈值与置信度模型输出结果变化不大，仅靠现有的模型无法对其进行有效分离，还需进一步优化模型结构。