基于双欧拉角的UKF组合导航滤波算法

赵仁杰, 胡柏青, 吕 旭, 田佳玉

(海军工程大学电气工程学院, 湖北 武汉 430033)

0 引 言

组合导航技术通过对多种导航系统信息综合处理,有效克服了单一系统局限性,提升了导航的精度与可靠性,被广泛应用在航空航天、武器装备、无人系统等领域[1]。目前,捷联惯性导航系统(strapdown inertial navigation system, SINS)/全球卫星导航系统(global navigation satellite system, GNSS)是最常见的组合导航系统之一,两者良好互补,具有导航信息全面、动态性好、自主性强、精度高等优势[2-3]。

信息融合是组合导航的关键,其实现依赖于现代滤波技术,其中最主要的手段是卡尔曼滤波[4]。根据系统状态选取不同,卡尔曼滤波可分为直接法和间接法。其中,间接法系统状态为导航参数误差,模型经过线性近似,容易处理,在工程中应用广泛,而直接法直接选取导航参数作为状态,可以无损传递运动信息,但状态方程非线性,存在滤波器设计复杂、计算量大缺点[5-6]。随着计算机与非线性滤波技术的发展,扩展卡尔曼滤波(extend Kalman filter, EKF)、无迹卡尔曼滤波(unscented Kalman filter, UKF)、粒子滤波(particle filter,PF)等非线性滤波算法[7-9]逐渐凸显出直接法的优势。其中,UKF利用Sigma点采样近似估计非线性函数概率密度,避免了EKF模型线性化以及求解复杂雅克比矩阵的缺点,具有适中的计算量和较高的滤波精度。

在组合导航系统中,姿态参数和其他导航参数相耦合,无法直接获取,需要通过状态滤波估计得到,其估计好坏直接影响着系统精度,因此姿态估计研究十分重要。其中,姿态描述是研究基础,常见表示方法有方向余弦矩阵、四元数、欧拉角、罗德里格斯参数(Rodrigues parameter, RP)和修正RP(modified RP, MRP)等[10]。方向余弦矩阵可以全姿态表达,但求解计算量大;欧拉角、RP和MRP都是维数最小的姿态表示法,但存在奇异性;四元数凭借着全局非奇异、运动学方程为线性等优势,成为应用最广泛的姿态表达形式[11-12]。

四元数参数之间相互并不独立,存在着规范性约束,若直接与非线性滤波结合,容易造成滤波发散。对此,Crassidis等[13-14]提出四元数无迹估计器(unsented quaternion estimator, USQUE)算法,利用分层滤波成功解决了约束问题,但算法结构复杂,计算量大。文献[15]提出一种改进的USQUE算法,通过四元数与MRP线性变换,降低了计算量。Karlgaard等[16]采用MPR表示姿态,通过MRP和其影子MRP相互切换避免了奇异性。后续许多学者也对此展开了深入研究[17-18]。目前,在非线性姿态估计中,姿态表示常用四元数和Rodrigues参数族,很少采用欧拉角,但欧拉角意义明确,参数独立且求解姿态矩阵无需正交化处理,针对奇异性问题,黄雪樵[19]提出双欧法,仿真表明该方法可以有效避免奇异性;陈廷楠等[20-21]证明双欧法克服欧拉方程的奇异性要优于四元数法;文献[22]对双欧法进行改进,实现了飞行器的任意姿态连续解算;Ran等[23]将双欧法应用在水下航行器的非线性对准中,取得较好效果。

针对USQUE算法的缺点,本文采用双欧拉角姿态表示,提出一种基于双欧拉角姿态表示的无迹卡尔曼滤波(dual-Euler unscented Kalman filter, DEUKF)非线性滤波算法,比较分析了两种算法的姿态估计过程,并在SINS/全球定位系统(global positioning system,GPS)直接式组合导航中应用,仿真和车载实验结果表明所提算法具有较好的精度，且计算量明显减小。

1 姿态表示

定义坐标系:导航坐标系取“东-北-天”地理坐标系,记为n系,载体坐标系为b系,取“右-前-上”,惯性坐标系为i系,地球坐标系为e系。

1.1 四元数

四元数是一种特殊的四参量姿态表示法,具有全局非奇异性,定义为q=[q0，ρ]T,q0为标量,ρ=[q1，q2，q3]T为三维矢量。姿态四元数微分方程表示如下:

(1)

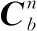
(2)

式中:(·×)表示反对称阵。

1.2 RP族

RP族是一种三参量姿态表示法,与旋转矢量和姿态四元数关系如下:

Rfamily=etan[φ/(2N)]=fρ/(a+q0)

(3)

N=1时,Rfamily=etan(φ/2),表示RP,此时,f=1,a=0;N=2时,Rfamily=etan(φ/4),表示MRP,一般记作σ,此时,f=a=1;N>2时,Rfamily表示高阶RP(high order RP,HORP)[15,18]。

MRP与四元数q的转换关系如下:

σ=ρ/(1+q0)

(4a)

(4b)

1.3 欧拉角

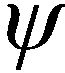
(5)

(6)

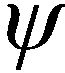
1.4 双欧拉角

分析式(5),在θ=±π/2处,姿态微分方程无法求解,存在奇异性,这也是欧拉角无法全姿态表达的原因。双欧法通过重新定义一组反欧拉角,利用正、反欧拉角切换,有效避开了奇异点。

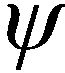
(7)

(8)

式中:符号标记方式同第1.3节。

比较式(5)和式(7),在正欧拉微分方程中,θ=±π/2为奇异点,而在θ=0和θ=±π处,cosθ=1,方程求解精度高,称为精华点;在反欧拉微分方程中,γr=±π/2为奇异点,在γr=0和γr=±π处,cosγr=1,是其精华点。

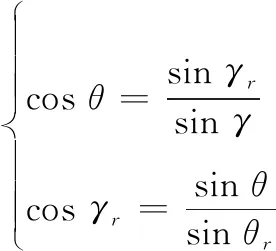
(9)

分析式(9),θ→±π/2,γr→0或γr→±π;γr→±π/2,θ→0或θ→±π,可以看出,正欧拉微分方程的奇异点对应反欧拉微分方程的精华点,而反欧拉微分方程的奇异点对应正欧拉微分方程的精华点,两者相互倒挂。

双欧法工作原理是到达正欧拉微分方程奇异点前,通过姿态矩阵进行正、反欧拉角切换,再利用反欧拉微分方程进行更新,反之亦然,进而实现全姿态工作。文献[25]验证了正、反欧拉角的最佳切换角度为±π/4和±3π/4,即精华点和奇异点区间的二等分点是最佳切换点。切换示意图如图1所示,图中字母A表示精华点,B表示切换点,C表示奇异点,白色区间代表微分方程的精华区,阴影区间代表奇异区。对于正欧拉微分方程,图1对象是正欧拉俯仰角θ,而对于反欧拉微分方程,对象为反欧拉横滚角γr。

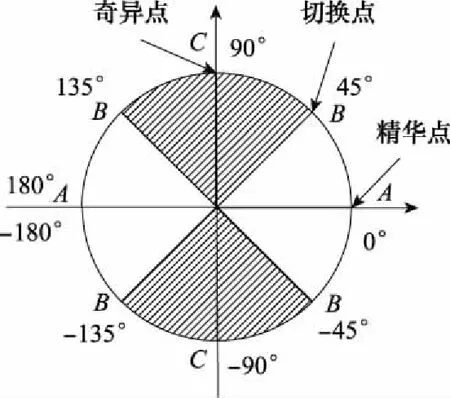
图1 切换示意图Fig.1 Switching diagram

2 非线性滤波算法

2.1 UKF算法

考虑如下离散非线性系统:

(10)

式中:状态方程非线性,量测方程线性,噪声为加性噪声。其中，Xk和Yk分别表示k时刻的n维状态量和m维量测量;f(·)为非线性状态函数；Hk为量测矩阵；Wk-1和Vk分别为系统噪声与量测噪声向量,两者互不相关,且满足如下关系:

(11)

式中:δkj为克罗内克函数。

对于上述非线性系统,给出UKF算法步骤。

步骤 1状态初始化

步骤 2时间更新

(12a)

χi,k/k-1=f(χi,k-1/k-1)

(12b)

(12c)

(12d)

式中:χi,k-1/k-1为k-1时刻的sigma点;sigma(·)为sigma点采样方程,可表示为

(13)

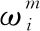
(14)

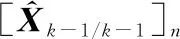
步骤 3量测更新

(15a)

(15b)

Pk/k=(In-KkHk)Pk/k-1

(15c)

2.2 USQUE算法

利用四元数进行非线性滤波姿态估计,虽然不会出现奇异,但存在着归一化约束以及滤波方差矩阵匹配约束问题。USQUE算法将滤波分成内外两层,内层采用误差MRP传递采样点,外层利用四元数完成姿态更新,有效解决了上述问题。给出具体流程如下:

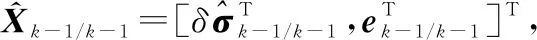
为简化说明,下文仅对USQUE算法的关键姿态估计流程进行介绍[26]。

(1) 时间更新

外层姿态更新:

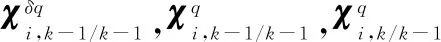
外层姿态更新过程可分为3步。

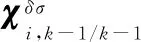
(16)

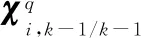
内层姿态递推可分为2步:

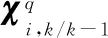
(17)

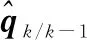
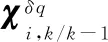
状态估计及均方误差一步预测同式(12c)和式(12d)。

(2) 量测更新

量测更新过程参照UKF算法。

(3) 姿态更新

(18)

2.3 DEUKF算法

双欧法利用正、反欧拉微分方程奇异点和精华点倒挂性质,通过正、反欧拉角切换来实现全姿态表达。本文提出的DEUKF算法设计了一种新的姿态估计流程,介绍之前,给出以下两个切换判断条件,与文献[24]仅用θ作为切换条件判断对象有所不同。

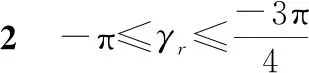
图2 DEUKF算法姿态估计流程图Fig.2 Flow chart of attitude estimation of DEUKF algorithm

2.4 算法比较

在直接式组合导航中,USQUE和DEUKF算法均在UKF框架下,利用SINS基本方程进行状态滤波更新,理论上没有模型近似,滤波精度较高,不同之处在于姿态表示和估计流程。

3 仿真试验研究

3.1 SINS/GPS组合导航模型

本文建立SINS/GPS直接式组合导航系统模型,由SINS和GPS测量载体运动参数,构建系统状态方程和量测方程,通过UKF滤波器估计出导航参数,系统结构如图3所示。

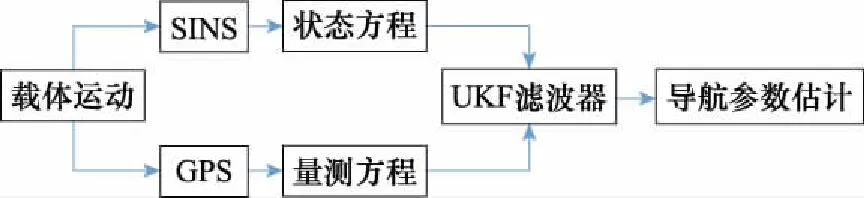
图3 SINS/GPS直接式组合导航结构框图Fig.3 Structure diagram of SINS/GPS direct integrated navigation system

系统状态模型采用SINS基本方程,不同姿态表示的微分方程见第1.1节,比力方程和位置微分方程具体如下:

(19)

(20)

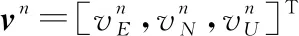
对于中低精度SINS,系统状态一般还需考虑器件误差、陀螺仪漂移和加速度计零偏。陀螺仪和加速度计误差方程分别为

(21a)

(21b)

(22a)

(22b)

量测模型采用速度和位置松组合模式,得到线性离散量测方程:

(23)

式中:ηv k和ηp k分别是零均值速度和位置高斯白噪声。

3.2 仿真试验

为验证算法有效性,利用轨迹发生器模拟飞机大机动运动,其轨迹如图4所示,包含匀速、加速、爬升、转弯、俯降、滚转等状态。图5和图6分别给出载体姿态和速度变化。轨迹初始地理位置参数为东经108.91°，北纬34.25°，高度为1 000 m,初始姿态角为0°,初始速度为0 m/s,仿真步长为0.01 s,总时长为700 s。

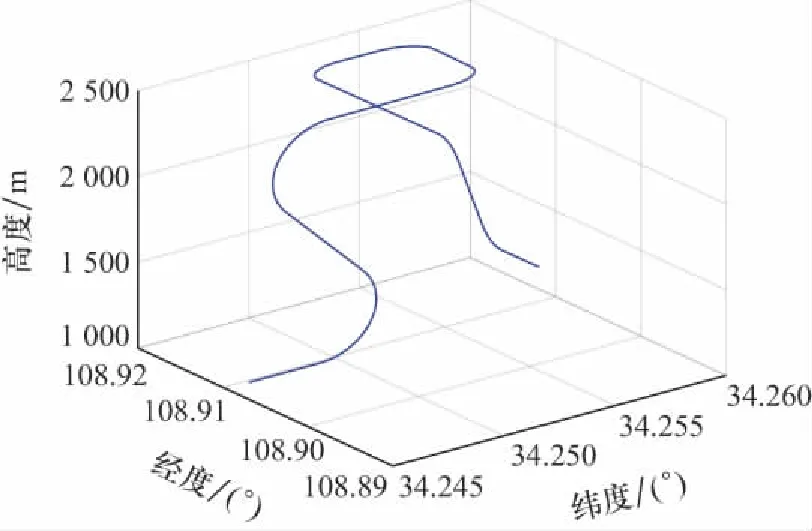
图4 运动轨迹仿真Fig.4 Simulation of motion trajectory

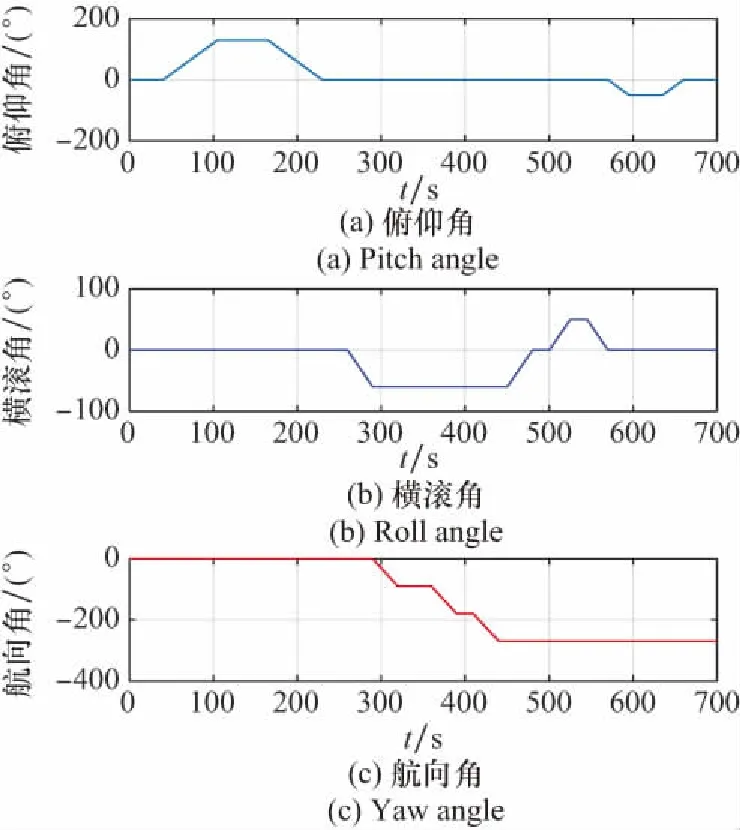
图5 载体姿态变化Fig.5 Change of carrier attitude

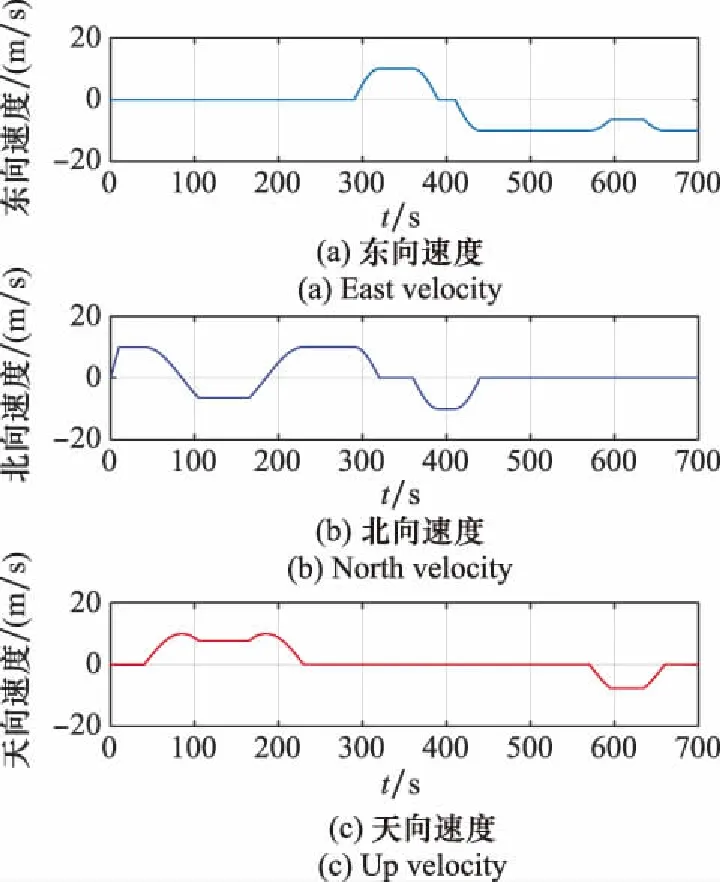
图6 载体速度变化Fig.6 Change of carrier velocity

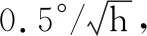
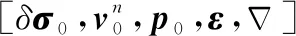
模型采用速度和位置松组合,算法对速度和位置状态估计比较准确,因此仅对比分析两种算法姿态估计效果,参考运动姿态信息,给出姿态误差对比结果,如图7和图8所示。其中,直线表示USQUE算法,虚线表示DEUKF算法。

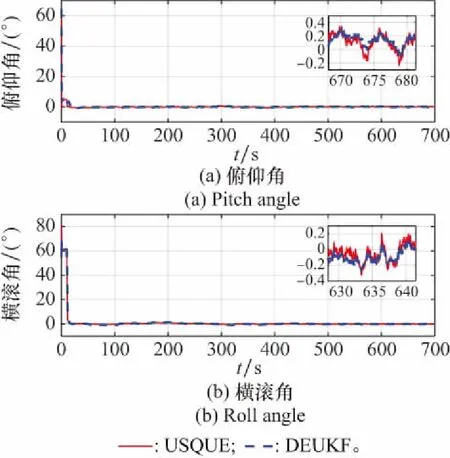
图7 俯仰角和横滚角估计误差对比Fig.7 Comparison of pitch angle and roll angle estimation errors

从图7和图8中可以看出,对于中低精度SINS/GPS组合导航系统,在大初始姿态误差角下,两种算法的姿态滤波收敛速度较快,其中俯仰角和横滚角均在20 s左右稳定收敛,航向角估计效果相对水平姿态角要差,在20 s左右快速收敛至0.6°以内,在450 s左右达到稳定,误差收敛到0.1°以内,原因在于航向角和水平姿态角估计精度分别取决于陀螺仪和加速计的性能;对比仿真结果,两种算法的水平姿态角滤波估计精度相当,航向角误差收敛趋势一致,其中USQUE稳态精度略优于DEUKF,但在运行时间上,DEUKF相比USQUE滤波结构简单,计算时间明显减小。

图8 航向角估计误差对比Fig.8 Comparison of yaw angle estimation error

为验证算法稳定性与有效性,保持初始条件不变,进行50次蒙特卡罗仿真试验,用均方根误差(root mean squared error,RMSE)和平均运行时间来衡量算法的性能,RMSE的表达式为

(24)

姿态RMSE和算法运行时间如表1所示(CPU of Inter core i5-8250U,1.60 GHz,Matlab R2015a)。仿真结果表明,DEUKF算法航向角均方根误差为5.83′,USQUE略优于DEUKF，为1.72′;若以平均运行时间衡量算法的计算量,USQUE为394 s,DEUKF为160 s,由此可见,本文所提算法计算量明显减小,验证了第2.4节的理论分析。

表1 姿态RMSE与算法运行时间

相比USQUE每一次迭代滤波都要进行两次内层误差MRP与外层四元数相互切换,每一时刻DEUKF只利用一组欧拉回路进行滤波更新,且仅在相应欧拉角超出精华区时进行切换,实际次数并不多,其正、反欧拉角切换和姿态角均方误差变化分别如图9和图10所示。在图9中,flag为标签,flag=0和flag=1分别表示正、反欧拉角,对照图5载体姿态角(正欧拉角),第一次切换发生60 s左右,此时θ超出45°,切换进入反欧拉回路,以γr作为判断对象,在200 s左右,θ开始进入45°以内,γ为0°,由式(9)可知,sinγr=cosθsinγ,γr也为0°,仍在反欧拉微分方程精华区,不同于文献[24],此处无需切换,第二次切换在280 s左右,此时,θ为0°,γ开始小于-45°,γr也开始小于-45°,进入奇异区,反欧拉角切换为正欧拉角,后续切换分析同上。

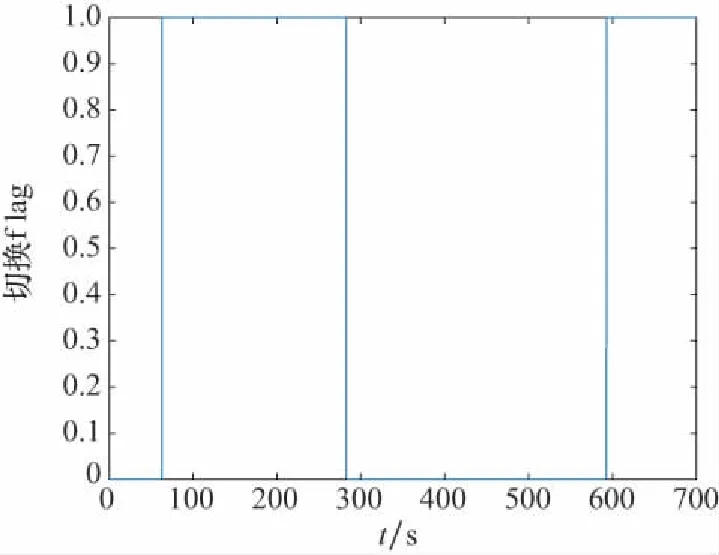
图9 正、反欧拉角切换图Fig.9 Switching diagram of positive and reverse Euler angles

分析图10,可以看出滤波中姿态的均方误差快速收敛,在正、反欧拉角切换处并未出现波动,可见切换对姿态均方误差的影响较小。

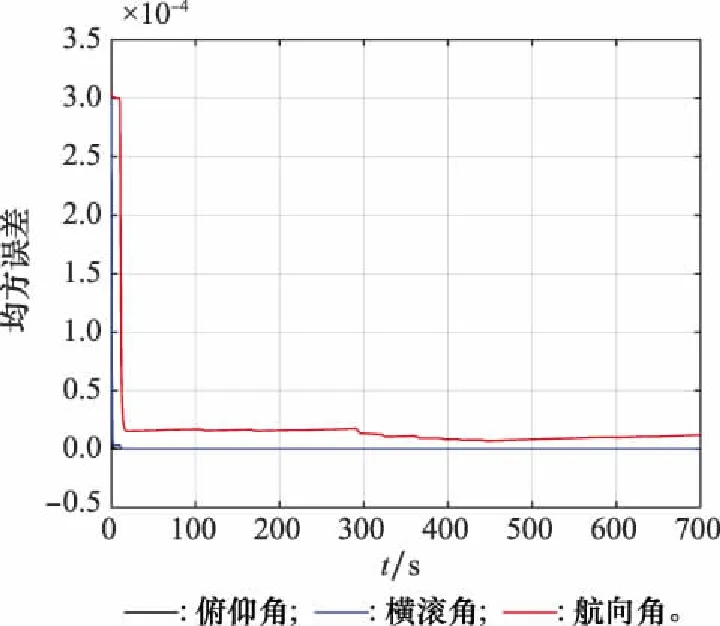
图10 姿态均方误差变化图Fig.10 Changing diagram of attitude mean square error

3.3 车载实验

大机动仿真试验表明,DEUKF滤波精度较高、计算量小,若将算法运用在小机动性场景中,状态切换减少,理论上更具优势,为验证有效性,进行车载组合导航实验。

搭建车载实验平台,主要由XW-ADU7612型高精度航向姿态参考系统(attitude and heading reference system, AHRS)和XW-IMU5220型微机电惯性导航系统(micro electro mechanical system,MEMS)组成,其中,AHRS包含光纤陀螺仪、硅加速度计及GPS接收天线,GPS有效工作时,AHRS提供的精度指标为姿态0.05°,航向0.1°,速度小于0.1 m/s,定位小于2 m;主要性能指标如表2所示。

表2 XW-IMU5220主要性能指标

车载实验在空旷的操场上进行,绕操场跑道行驶150 s,轨迹和速度分别如图11和图12所示,运动轨迹高度基本相同且天向速度为0 m/s。

图11 实验运动轨迹Fig.11 Experiment motion trajectory

图12 车辆运动速度Fig.12 Velocity of the vehicle motion

运动全程GPS信号接收良好,利用GPS测得的东向、北向速度和经/纬度位置信息作为观测量进行组合导航,系统噪声和量测噪声方差根据传感器指标和经验值进行设置,得到两种算法姿态估计效果如图13～图15所示,其中实线为AHRS提供的姿态参考基准,点划线和虚线分别表示USQUE和DEUKF算法。

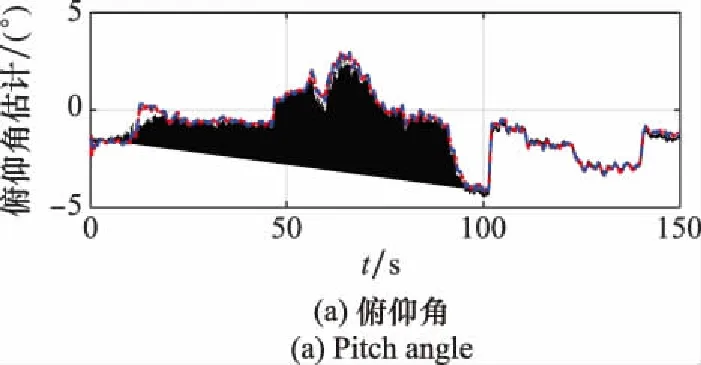
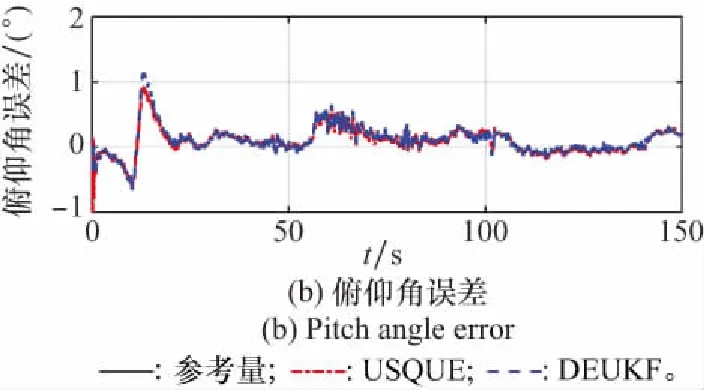
图13 俯仰角与估计误差Fig.13 Pitch angle and estimation error

图14 横滚角与估计误差Fig.14 Roll angle and estimation error

图15 航向角与估计误差Fig.15 Yaw angle and estimation error

从图13～图15中可以看出,在MEMS/GPS直接式组合导航车载实验中,两种算法的姿态估计精度相当,由于航向角可观测性弱,在载体运动直线段,航向角基本不变,滤波估计效果不好,估计误差有增大趋势,最大误差约达到9°,当载体转向时,可观性增强,航向角快速收敛,误差减小;相比航向角,水平姿态角自身可观测性较强,两种算法俯仰角和横滚角滤波估计误差在0.5°以内波动,没有明显发散趋势。

参考AHRS提供的姿态,给出两种滤波算法姿态RMSE和运行时间如表3所示。结果表明,水平姿态角估计效果要比航向角好,对于航向角,USQUE算法估计精度略优于DEUKF,分别为3.334°和3.426°,但在算法运行时间方面,DEUKF时间约为56 s,USQUE约为97 s,分别为总实验时间的37.3%和64.7%,可见DEUKF的计算量更小。

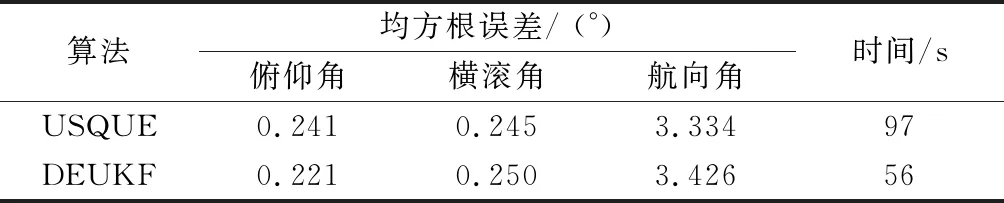
表3 姿态RMSE和算法运行时间

4 结 论

USQUE算法利用姿态四元数和误差MRP相互转换进行双层滤波,有效避免规范性约束的同时,计算负担明显加重,实时性较差,相比姿态四元数,欧拉角维数更小,求解姿态矩阵无需正交化处理,本文采用无奇异的双欧拉角进行姿态表示,提出一种基于UKF框架的DEUKF组合导航算法,并同USQUE算法进行理论分析对比,给出了具体的切换条件和流程。最后,通过SINS/GPS直接式速度与位置松组合导航仿真和车载实验,得出相比USQUE算法,DEUKF算法计算量小、实时性好,水平姿态角估计精度与USQUE相当的结论,可以为实际场景组合导航算法的选择提供一种参考。