复杂网络视角下的城市热点区域空间交互分析

周 博，马林兵

（1.广州市城市规划勘测设计研究院，广东 广州 510060；2.中山大学地理科学与规划学院，广东 广州 510275）

城市热点区域是居民出行起讫点较集中、交通流量较大，并能吸引居民频繁到访的区域，热点区域的时空分布和内在联系是城市规划、交通和应急等政府部门行使特定职权、配置公共资源的重要参考，同时也是推进城市治理体系和治理能力现代化过程中的决策依据。空间中任何事物都不是孤立存在的，其必以物质、能量、信息等形式在空间不同位置之间发生着作用和联系，这种地理过程被称为空间交互[1]。复杂网络作为一种描述自然、社会及工程技术中相互关联的理论，其严谨的数理知识体系和全面的基础统计指标，为研究现实网络系统的空间交互提供了全新视角[2]。近年来，随着时空轨迹数据的可获取性增强、数据挖掘技术的推广应用和城市地理学的网络转向，促使城市热点区域[3-4]、城市功能及网络结构[5-9]成为地理学、城市规划等学科的研究热点。

现有城市热点区域研究多是基于移动定位大数据讨论热点区域如何识别、分布和演变，网络结构相关研究主要集中在宏观位序关系、节点联系特征和时序变化等方面。带有时空标记的、个体粒度的出租车轨迹数据具有空间交互特性，其累积效应在某种程度上就是热点区域的空间表现。学术界很少从复杂网络视角将出租车流动的交互行为嵌入到居民出行的地理空间，缺乏对出租车轨迹映射的热点区域空间交互关系进行全面定量表达以及微观地理解释。

本文以大样本量的连续型出租车轨迹数据为基础，首先基于数据场理论识别节假日和工作日两种典型时间的热点区域空间分布，然后从复杂网络视角分析热点区域的空间交互，以期弥补静态城市规划对居民时空出行和城市交通演变特征规律解读不准确、不深入的弊端，研究结果可为城市精细化管理、区域功能优化提升、智慧城市升级等提供支撑和依据。

1 研究区与数据

1.1 研究区

选取深圳市9个行政区和1个新区（不含深汕特别合作区）作为研究区，深圳作为典型的高度城市化、年轻化地区，外来人口多，常被称为移民城市和候鸟城市。近年来，深圳人口规模持续增长，人口密度长期处于全球城市前列。城市局部区域逐渐暴露出社会分异、空间隔离、交通拥堵等社会问题，对深圳城市规划水平和社会治理能力提出了挑战。

1.2 数 据

出租车GPS轨迹数据获取原理是通过在车辆上装载车用GPS设备，由该设备按照特定规则向交通信息中心实时传送车辆位置、速度、方向和载客状态等相关信息，本文选用深圳市节假日和工作日共2 d（2015年5月1日和6日）约15 500辆正常运营的出租车GPS轨迹数据作为实验数据集。由于原始数据的采样间隔为30 s，且24 h不间断，并以文本格式储存，而热点区域表示更多居民上车或下车这一瞬间行为所发生的空间位置，原始轨迹数据针对热点区域识别这一特定需求存在一定程度的冗余和异构问题。因此，对GPS轨迹数据需进行格式转换、噪点清除、上下车点提取等必要的预处理。

2 研究方法

2.1 基于数据场理论的城市热点区域识别方法

场的概念源自物理学，用于描述物体间的非接触作用。每个对象都相当于空间中具有一定质量的数据粒子，其周围存在着一个作用场，场中的所有数据粒子都会受到场中其他数据粒子的场作用力，由此在整个空间上形成一个数据场[10]。势是物理学描述场随空间位置变化的重要物理量，将物理场中的势函数引入到数据场中，用来定量表征数据对象之间的相互作用程度，用等势线或等势面描述数据空间连续分布特征。

出租车上下车轨迹点数据可看作是位置点的一个时间序列，高斯函数具备作为数据场势函数的基本性质，引入能够反映势值随时间变化的标准化时差系数，将时差系数作为权重参数添加至势函数公式，从而将空间数据场扩展为时空数据场，即可定量表征势值的时空衰减效应。时空数据集P中的任意轨迹点Pi的势值计算公式为：

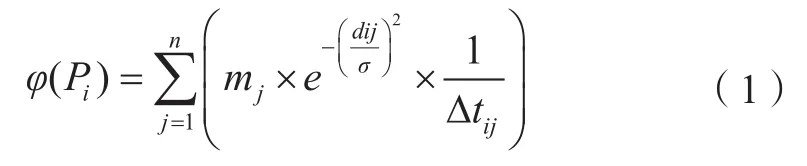
式中，mj表示轨迹点Pj的质量；dij表示轨迹点Pi和Pj之间的距离，为数据对象之间相互作用影响的半径，称为影响因子。淦文燕等[11]提出了一种基于信息熵的σ优选方法，通过实验将势熵最小时的σ（值为0.3）当作时空数据场中的影响因子。Δtij为Pi和Pj两个轨迹点归一化后的时差系数[4]，其计算公式为：

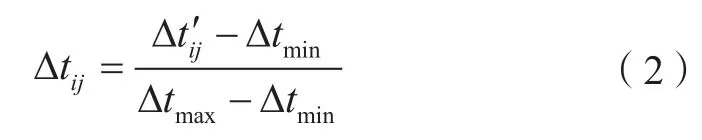
式中，Δt′ij表示轨迹点Pi和Pj的时间差值；Δtmin表示时空轨迹数据集P中任意两点时间差值的最小值；Δtmax表示时空轨迹数据集P中任意两点时间差值的最大值。

综上，基于数据场理论探测热点方法的主要思想是：将研究区中的每个上下车点看作一个质点，且认为质点的质量均相同，运用时空拓展后的势函数计算该点势值，然后对含有势值的上下车点进行空间插值分析，从而使得研究区内呈现连续的势值分布，若某区域上下车点势值越高，则表明该区域的吸引力越大，即该区域附近集聚了大量的上下车点，可认为该区域是城市热点区域，将势值局部极大值点视作热点区域中心。为了规范描述面状热点区域的空间位置，同时便于热点区域空间交互网络的制图表达，后续分析中用热点区域中心所在地理位置代表面状热点区域，并将该中心的地理位置抽象为热点区域空间交互的网络节点。

2.2 复杂网络视角下的空间交互分析方法

复杂网络理论最早起源于1736年瑞士数学家欧拉提出的“柯尼斯堡七桥问题”，复杂网络可看作是若干可抽象为点和点之间连线的几何图形，现实世界的很多实际生产生活问题都能够代入到这种几何图形中，点代表对象或者具体事物，连线代表对象之间的关系或联系[12]。

2.2.1 基本统计指标

复杂网络的统计指标能定量表达空间交互中网络节点和边所扮演的角色。基本统计指标主要包括度与度分布、平均路径长度和聚集系数。

1）度与度分布。节点的度与该节点的重要性或影响力呈正相关，是描述一个节点与网络中其他节点直接联系的能力，其值是与该节点连接的边数总和。有向图中，节点的度由出度和入度两部分组成，节点νi的度定义为：

式中，N为节点数（下同），表示νi节点和νj节点之间的连边权重。

在有向网络中，净流量比常用来表示由其他节点净流入某节点的占比，在一定程度上反映了节点的影响力。净流量比（NFR）定义为：

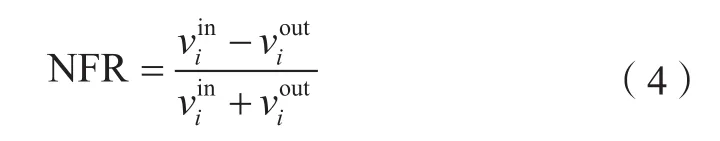
式中，为流入强度；为流出强度。

网络中节点的度分布情况通常用分布函数p(k)来描述，p(k)表示网络中度为k的节点在整个网络中所占的比例。一般地，用幂律形式p(k)∝k-γ（幂指数通常为2≤γ≤3）来描述复杂网络的度分布性质。

2）平均路径长度。连接网络中两个节点νi和νj的最短路径上的边数称为两节点之间的距离，记作dij。平均路径长度L就是对网络中任意两个节点之间的距离取平均值，该指标反映了网络的集散程度，能够有效刻画复杂网络的整体特性。网络的平均路径长度定义为：

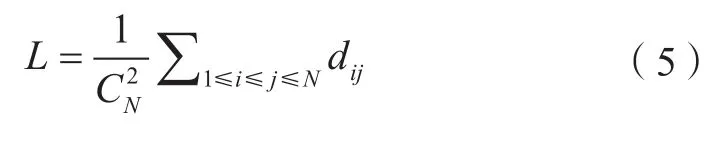
3）聚集系数。网络节点的聚集系数Ci的计算方式是与该节点相邻的所有节点之间实际存在的边数Ei与这ki个节点之间最多可能边数的比例。节点νi的聚集系数Ci定义为：

类比于平均路径长度，网络的聚集系数C则是对网络中所有节点νi的聚集系数取平均值，该指标是网络集聚性的直接体现，也可以理解为同一个节点的邻节点仍然是邻节点的可能性大小，反映了网络的局部特性。网络聚集系数C定义为：

显然，0≤C≤1。当所有的为孤立节点，即没有任何连接边时，C=0；当且仅当网络是全局耦合时，即网络中任意两个节点都直接相连，C=1。

2.2.2 社区发现

社区发现的本质是图划分问题。大量研究表明，网络中性质相同或相近的节点往往连接在一起，通常将性质相近的节点以及节点之间的连边所构成的子图称为社区。社区发现是复杂网络分析中的重要方向，社区发现的广泛应用得益于Newman提出了一种模块度的概念，从而产生了一个定量评价指标度量网络社区划分的合理程度量[13]。模块度计算公式为：

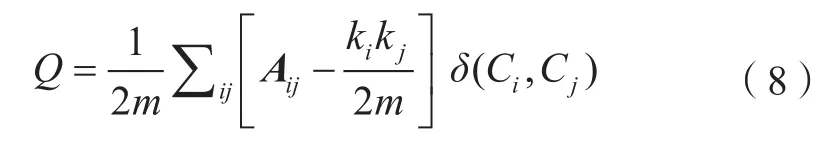
式中，m为网络中边权值总和；A表示网络的空间邻接矩阵；Aij=1代表节点和节点之间存在连边，否则不存在连边。ki，kj为节点i和节点j的度数，Ci为节点i属于某个社区的编号，当且仅当时Ci=Cj，δ(Ci,Cj)=1。模块度值Q取值范围在0到1之间，其值越接近1，表示网络划分出的社区结构越明显，也就是社区划分越合理。

综上，复杂网络视角的空间交互分析方法的主要原理是：以热点区域中心为节点，以出租车在热点区域间的上下车关系为边，以上下车次数作为网络边权值构建热点区域空间交互的有向加权网络。通过复杂网络基本统计指标分析热点区域网络的全局特性，然后基于社区发现的思想揭示热点区域网络内部聚类特征和交互异质性。

3 结果与分析

3.1 热点区域整体特征

截取节假日和工作日7：00～9：00时间段，基于数据场理论方法进行势值计算并绘制等势线（图1）。势值高的区域可认为是热点区域，等势线可直观地描述数据的分布[14]。

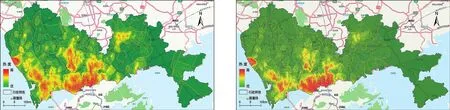
图1 热点区域探测结果

由图1可知，节假日与工作日势值结果明显不同，即热点区域在整体表现、空间特征、冷热差异以及所在地理位置等诸多方面均呈现差异化特征（表1）。究其原因：5月1日是五一长假的第一天，节假日大部分人行程安排相对自由，居民通常乘坐出租车前往市内热门景点观光旅游或通过机场、口岸、火车站等交通枢纽前往外地，没有外出旅游的市民也倾向于就近出行参与社交活动。工作日热点区域高度集中在商贸服务功能最突出的福田和罗湖，除此之外，宝安-南山、龙华-福田和龙岗-罗湖这3处交界成为居住功能主导的热点区域。职住分离和就业可达性差异共同促成了“居住地—工作地”的典型早高峰通勤模式。

表1 热点区域特征

3.2 热点区域网络空间交互分析

3.2.1 网络整体表现

将势值局部极大值点作为网络交互可视化分析的节点，共选取21个热点区域，按照势值相对大小对节点进行顺序编号（即编号1～21），势值越大，编号数值越大。对节假日和工作日热点区域空间交互网络的基本统计特征进行定量对比（表2）。

表2 热点区域空间交互网络基础统计描述

平均路径长度可表征居民在热点区域之间出行活动的来往频率和远近程度，聚集系数模拟分析热点区域网络和各节点之间的集团特征，较短的平均路径和较大的聚集系数表明热点区域网络满足小世界效应。节假日的聚集系数和平均路径长度均大于工作日，表明节假日热点区域网络连接多样性更强，网络直径较大，不同热点区域之间交互距离更长，范围更广。节假日度平均计算结果小于工作日，说明热点区域网络的平均连边数量不及工作日，即网络交互稳定性稍弱于工作日。

深南大道作为深圳道路网络中东西走向的“大动脉”，也是原关内关外的分界线。对节假日和工作日21个热点区域空间交互次数即边权值进行可视化分析，用直线连接表示热点区域之间的联系，直线越粗，表示由两热点区域间来往的人流量越大，联系越紧密。考虑到热点区域内部交互的实际情况，按区域内交互次数进行分级可视化，热点序号所在圆圈越大，表示该热点区域内部交互越频繁（图2）。

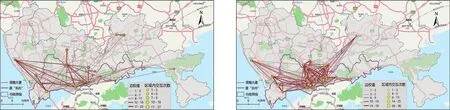
图2 热点区域空间交互可视化（标注深南大道和原关内区域）

对比节假日和工作日可以发现，节假日热点区域净流量比和边权值差异较大，边权值较大的连边集中在宝安机场、福田口岸、罗湖口岸（深圳火车站）、深圳北站和深圳东站等交通枢纽之间。另外，节假日热点区域交互网络按照边权值可分为两个“团体”，第一个是“福田区中心-罗湖区中心-深圳北站”的强三角关系；第二个则是“宝安机场-宝安区中心-深圳湾公园”的短距离条状联系带。工作日净流量比和边权值差异相对不大，但局部区域空间交互明显密集，尤其是以深圳市中心城区为圆心，一定距离为半径的近似圆形区域，故边权值连线在图中表现为“毛线团”状。

从节假日和工作日共性表现来看，热点网络中与其他节点有大量连接的节点（即集散节点）占少数，多数节点之间连接较少，新的节点更倾向于与集散节点相连接，体现了一种“富者愈富”的趋势，网络内部具有明显层次性。尽管深圳热点区域空间交互网络范围分布很广，但其中任意两个热点区域之间却总能通过较短路径实现互连，且大部分热点区域存在以三角形连接的内部群聚倾向，存在局部抱团现象，热点区域空间交互绝大多数发生在原关内地区，表明热点区域空间交互网络具有一定程度的偏好依赖性，这表明热点区域网络具有复杂网络的无标度特征。

3.2.2 网络结构

借助复杂网络分析软件Gephi，基于模块度优化的方法，按照热点区域实际联系的紧密程度将节点划分为不同社区，分析热点区域空间交互网络的小集团形态和热点区域节点之间交互的抱团性（图3）。

图3 热点区域空间交互网络社区发现结果

由图可知，节假日和工作日热点网络自西向东均被分为3个社区，社区形态和社区内节点数量的差异体现了热点区域网络结构的时空异质性。节假日，宝安和南山区的热点区域组成了西部带状社区，深圳北站、福田口岸和罗湖口岸共同组成了紧密联系的中部圆形密集社区，盐田、大鹏、坪山和龙岗则组成平均路径相对较长的东部稀疏社区。物理距离更近的热点区域更有可能组成小团体且有更大的交互强度，说明地理学的距离衰减规律在居民出行领域中仍然起重要作用。工作日，社区形状均呈现带状，且每个社区中节点平均路径较长，显然这是职住通勤约束下的结果，表明功能错位对于网络分类的影响程度超过了距离邻近，区域功能相互补偿导致物理距离很远的区域交互也十分紧密。

3.2.3 典型节点

车公庙是工作日热点区域空间交互网络中影响力最大的节点，以车公庙节点（编号为17号）为圆心，半径15 km做缓冲区，进行可视化分析（图4）。

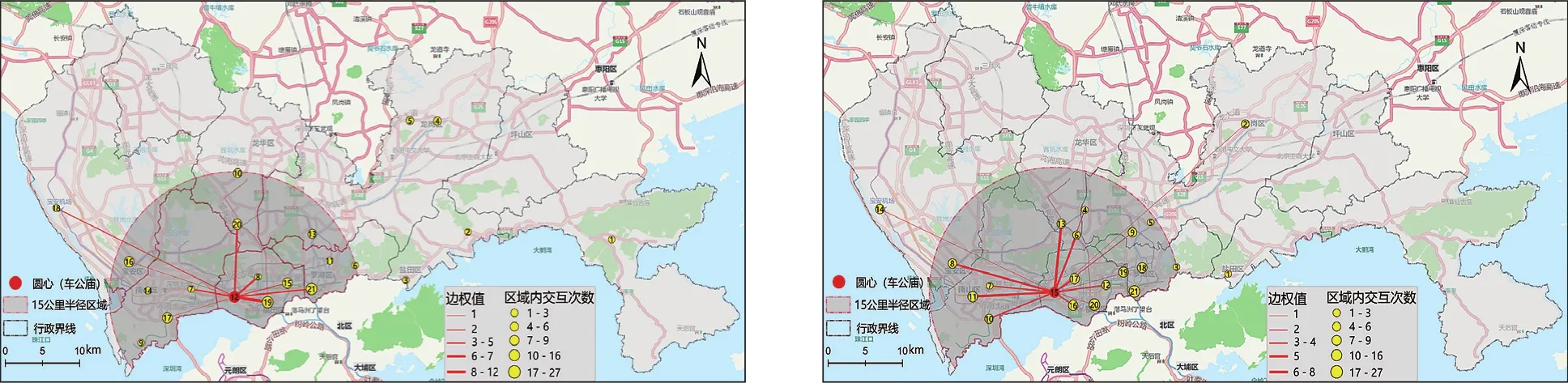
图4 车公庙节点空间交互可视化

以车公庙为圆心的15 km半径区域涵盖了绝大多数热点区域，热点区域是深圳居民出行和交通状态在两种典型不同时间上的间接映射，因此可将车公庙附近区域考虑作为城市交通应急和居民集散的控制指挥中心备用选址。车公庙在空间交互网络中扮演连接深圳东西方向“中转站”的角色，南北方向上主要和深圳北站及附近居住区交互较多。工作日和节假日不同之处在于工作日较节假日交互多样更强，边权值更大。 这是由于车公庙所在区域工作属性占主导地位。

4 结 论

空间交互是地理研究的传统议题，是认识城市空间一个“窗口”，基于复杂网络视角将居民出行的交互行为嵌入到城市空间，其本质就是以城市区域空间联系强度作为定量指标进行城市空间结构探测和区域功能识别的地理过程。本文围绕热点区域探测及空间交互这一主题进行可视化研究分析，旨在揭示城市组团结构、距离衰减效应、空间依赖等地理规律。结果表明节假日和工作日热点区域空间分布与驱动机制显著不同，节假日热点区域呈现多中心分布，热度变化相对平缓，与节假日居民个性化出行需求密切相关，工作日热点区域呈现单核集聚分布，热度差异存在明显的跳跃性，主要是职住分离和就业可达性差异共同导致的结果。热点区域空间交互网络满足小世界效应和无标度特征，热点区域的空间交互表现与该区域的主导城市功能密切相关，功能互补在一定程度上能够削弱空间邻近对于城市区域联系的影响程度，热点区域空间交互研究验证了合理的空间功能配置有助于城市发展。本文研究方法及结果对于优化城市区域功能、消除社会空间隔离、实现城市精细化管理有重要参考意义。