水位骤降影响下岸坡稳定性简化分析

贺林林，周 莉，梁 越

(1. 重庆交通大学 国家内河航道整治工程技术研究中心，重庆 400074；2. 重庆交通大学 水利水运工程教育部重点实验室，重庆 400074；3. 重庆交通大学 河海学院，重庆 400074)

水库、河流两岸存在许多潜在的滑坡体，在水位骤降情况下这些滑坡体更容易出现失稳破坏[1-2]。目前，实测统计资料表明，发生在水位消落期的库岸失稳破坏约占30%，一些大型滑动则往往发生在库水位达到最高峰后的急剧消落时刻[3]，如日本大约60%的水库滑坡发生在库水位骤降时期[4]。对于这些外部有库水位骤降作用的岸坡，水位骤降是影响岸坡稳定的主要外在因素之一[5-10]。在水位骤降过程中，坡体内浸水向坡体外渗流，对坡体产生渗透力作用，导致岸坡土体下滑力增大，岸坡稳定性降低，甚至产生失稳破坏。针对水位骤降过程中渗透力对岸坡稳定性影响的分析方法已有学者做了大量的研究工作，主要集中在极限平衡分析法和数值模拟分析法两方面[11]。毛昶熙等[12]通过对比分析条分法与有限元法已有计算成果，提出考虑渗流作用下土坡圆弧滑动的有限元法，并以渗透力取代条块周边的水压力，考虑了渗流方向及其力矩的影响。陈祖煜[13]通过分析已有试验和现场数据，提出库水位陡降时边坡稳定分析的总应力法，该方法简化了库水位骤降时坡体稳定性分析的过程。郑颖人等[1]简化了浸润线计算公式，并在此基础上推导了条分法中渗透力的计算公式，完善了库水位下降对岸坡稳定性影响的分析方法。刘新喜等[2]根据三峡库区滑坡地下水作用的力学模式，建立了渗透力作用下滑坡稳定性评价的不平衡推力法。唐晓松等[14]借助PLAXIS 有限元软件，基于强度折减法开展了渗流作用下的边坡稳定性分析。李湛等[15]采用强度折减弹塑性有限元数值分析，分析了边坡的临界失稳状态及安全系数。贾苍琴等[16]采用强度折减有限元方法与非饱和非稳定渗流有限元程序相结合方法分析了水位骤降时土坡的稳定性。年廷凯等[17]基于库水位下降过程及坡体内非稳定渗流条件，借助ABAQUS 有限元二次开发平台，建立了考虑地表水-地下水联动作用下的黏性土边坡强度折减有限元分析方法。可见，上述计算方法均是通过渗透力或孔隙水压力计算、渗流场与应力场耦合分析来考虑水位下降对岸坡产生的渗流作用，计算过程较复杂，不便于工程设计人员采用。而刘才华等[18]在库水位上升诱发边坡失稳机理研究中，采用Mohr-Coulomb 强度准则描述了孔隙水压力对土体应力状态的影响，分析了孔隙水压力作用下Mohr 应力圆变化情况，建立了水位上升后土体强度参数黏聚力变化的理论公式，基于此讨论了库水位上升过程中孔隙水压力对边坡稳定性情况，可为本文开展水位骤降影响下岸坡稳定性简化分析方法的研究提供参考。

因此，为了便于分析库水位骤降时渗透力对岸坡稳定性的影响，本文探索在计算过程中绕过渗透力的作用过程及渗透力的具体计算，直接计算渗透力作用后产生的影响结果的简化分析方法。基于对岸坡任一点的应力状态分析，建立将渗透力对岸坡稳定性影响简化为抗剪强度参数黏聚力c 减小的等效关系，并将此等效关系与强度折减法相结合，提出水位骤降产生的渗透力对岸坡稳定性影响的简化分析方法，并通过与传统极限平衡分析方法进行对比分析，验证其可行性。

1 渗透力影响等效关系建立

关于水位变化作用下岸坡稳定性分析，刘才华等[18]通过分析土坡中任一点的应力状态，进一步分析了水位上升后土体重度变化与黏聚力之间的关系。基于该研究思路，本文通过分析水位骤降过程中岸坡任一点的应力状态，建立岸坡内渗透力与抗剪强度之间的关系。水位骤降过程中，岸坡内浸水向岸坡外渗流，坡体受到渗透力作用，同时岸坡潜在滑动面抗剪强度因土体饱和度发生变化而发生改变，导致岸坡稳定性降低。假设滑动面强度参数的变化和渗透力是影响岸坡稳定性的两个相互独立因素，即在下面探讨渗透力的作用机理时不考虑滑动面强度参数变化，也不考虑土体重度的变化。

针对某一无限长均质岸坡，假设岸坡坡长方向也无限长（即假设岸坡坡长相对于所取研究点为无限长），首先取岸坡中任一点进行应力状态分析，该点至坡面的竖向距离为h，垂直距离为x（图1），然后根据弹性力学中已有关于平面问题中应力分量与体力分量等之间的关系式，可知应力分量、体力及单位渗透力j（其中j=γwsinβ）之间的关系，如图2 所示（其中土力学与弹性力学中采用的应力符号是相反的），最后可得岸坡任一点的平衡微分方程，即：

图1 岸坡任一点应力状态Fig. 1 Stress state at any point on bank slope

图2 岸坡任一点应力分量Fig. 2 Stress component at any point on bank slope

其中对于 σz求解，类似于土体中侧向土压力的求解[18]，即：

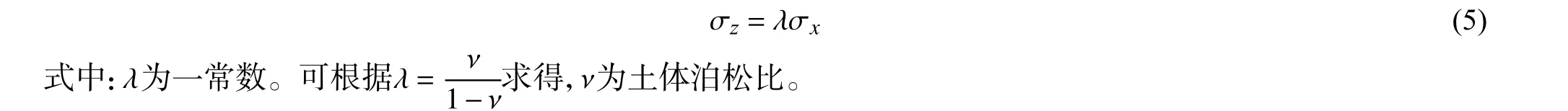
将式(4)代入式(5)可得沿z 方向应力 σz的表达式，即：

岸坡上任一点最大主应力和最小主应力为：

将式(3)～(6)代入式(7)，可得考虑渗透力作用时岸坡任一点的最大主应力和最小主应力，即：

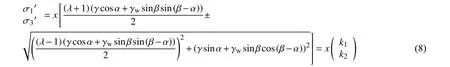
从式(8)可见，除x 为变量外，其他参数都是已知参数，因此 k1、 k2均为常数，且k1＞k2，即：

可见，考虑渗透力时岸坡任一点的主应力是x 的线性函数，可将式(8)简写为：

同理，在不考虑渗透力作用时，可根据图1 岸坡任一点的应力状态，再通过各应力分量与体力之间的关系，可得各应力分量表达式，即：

将式(12)代入式(7)可得不考虑渗透力作用时岸坡任一点的最大主应力 σ1和最小主应力 σ3，即：

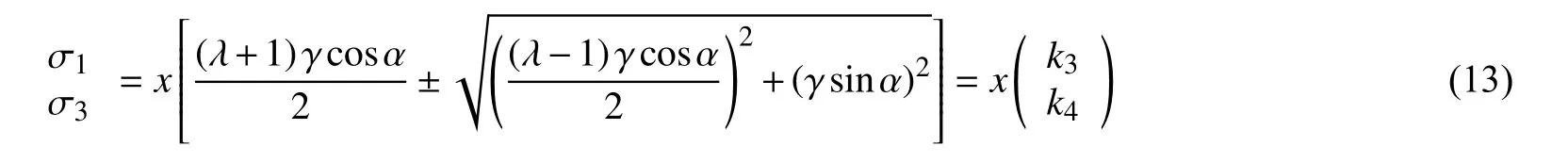
从式(13)也可见，除x 为变量外，其他参数都是已知参数，因此 k3、 k4均为常数，且k3＞k4，即：

同理，在不考虑渗透力作用时岸坡任一点的主应力也是x 的线性函数，可将式(13)简写为：

由Mohr-Coulomb 破坏准则可知，当岸坡处于极限平衡状态时，其潜在滑动面上任一点的应力圆与强度包络线相切，因此存在以下几何关系：

假定在不考虑渗透力作用时该岸坡已处于极限平衡状态，此时岸坡下滑力与土抗力大小相等，应力圆与τ=σtanφ+c相切，如图3 所示，将式(16)代入式(17)，可得：

考虑水位骤降对岸坡产生的渗透力作用时，岸坡下滑力将会变大，其滑动面上任一点的主应力 σ1、σ3的值增大到，如图3 中大应力圆所示，此时应力圆变大且向右移动，应力圆超出岸坡强度包络线范围，岸坡出现破坏。在这种情况下，若要保持岸坡仍处于极限平衡状态，则需要增大岸坡土体抗剪强度用于抵抗渗透力作用，因此，本文假设只增大土体黏聚力来增加土体抗剪强度，以提供抵抗渗透力作用（岸坡增加的下滑力）所需的土抗力，使岸坡在渗透力作用下仍处于极限平衡状态，则增大的抗剪强度与变大的应力摩尔圆相切，在图3 中作一条曲线τ′=σtanφ+c′与大应力莫尔圆相切，再将式(11)代入式(17)可得新几何关系：

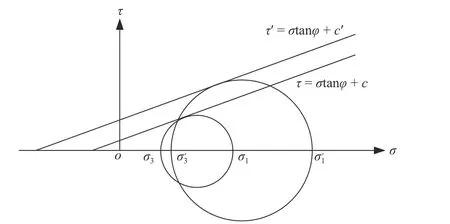
图3 应力圆与强度曲线Fig. 3 Stress circle and intensity curve

比较式(19)和式(18)可知c′＞c，再从图3 中可以看到在考虑渗透力作用后，τ′=σtanφ+c′与τ=σtanφ+c相互平行，因此两者抗剪强度之差为黏聚力之差 c1，且该黏聚力差值是用于抵抗水位骤降对岸坡产生的渗透力作用。为了更方便表示图3 中考虑渗透力作用时与不考虑渗透力作用时两者黏聚力之间的关系，进一步假设存在一个等效系数ξ，使考虑渗透力作用时的黏聚力 c′等于原始黏聚力c 与等效系数ξ的乘积，即：

分别将式(18)、(19)代入式(20)，可以得到等效系数ξ的计算式，即：

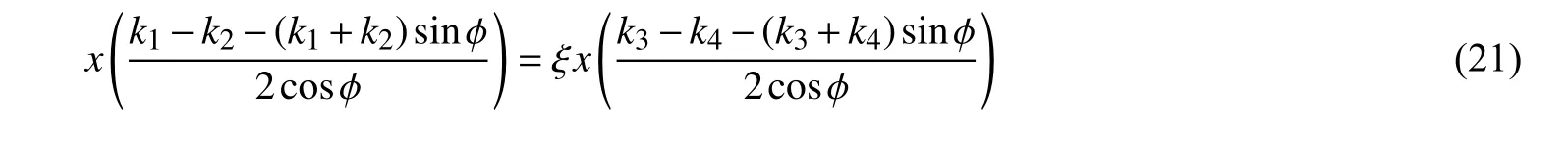
因此，由于抵抗水位骤降影响下渗透力作用而引起的黏聚力变化值 c1为：

对于不考虑渗透力作用且处于极限平衡状态的岸坡，若考虑渗透力作用后其下滑力将增大，则假设土体中将增加相应的土抗力来抵抗该部分新增下滑力以维持岸坡稳定，而这部分在渗透力作用下增加的下滑力可由式（23）表示，即黏聚力的变化量。基于此，为了简化考虑渗透力作用，将渗透力对岸坡稳定性的影响等效为土体强度参数黏聚力的降低，提出将渗透力作用简化为通过在岸坡土体原强度参数黏聚力上减去抵抗渗透力作用的这一部分黏聚力值 c1，得到一个考虑渗透力作用后等效的土体新黏聚力值，如下式：

式中： c′′为考虑渗透力作用后等效的土体新黏聚力值（kPa）。

2 简化分析方法建立

强度折减法最早由Zienkiewicz 等提出，在岩土工程领域得到了广泛应用。其定义为：使岸坡刚好达到临界破坏状态时，对岩土体的抗剪强度进行折减的程度，即安全系数为岩土体的实际抗剪强度与临界破坏时的折减后抗剪强度的比值。通过式(25)、(26)来折减岩土体的强度指标 cm和 φm，然后对岸坡进行数值分析，通过不断地增加折减系数，反复计算，直至达到临界破坏，此时得到的折减系数即为安全系数[19-20]。

式中： c 为原始黏聚力（kPa）； φ为土体原始内摩擦角（o）； cm为土体实际发挥的黏聚力（kPa）； φm为土体实际发挥的内摩擦角（o）； Fr为强度折减系数。

因此，将新的土体强度参数 c′′替换式（25）中原始黏聚力c，与强度折减法结合，即可建立考虑水位骤降下渗透力对岸坡稳定性影响的岸坡稳定性简化计算模型。

式中： ξ为等效系数，可由式（22）计算所得。

3 简化分析方法验证

3.1 均质岸坡稳定性分析

图4 均质岸坡剖面(单位：m)Fig. 4 Homogenous bank slope profile (unit：m)

为了验证简化分析方法，参照文献[21]选用在库水位骤降作用下的均质岸坡作为算例，如图4 所示。该岸坡高10 m，基底厚5 m，岸坡坡比为1∶2。岸坡土体物理力学参数为：c=10 kPa，γ=20.2 kN/m3，φ′=20o，饱和渗透系数k=5.4×10−7cm/s。岸坡最低水位位于坡底，初始水位为12.0 m，水位以1 m/d 的速度骤降至坡脚5 m 位置处。

ξ=1.46c′′=5.41 kPa

基于本文建立的简化分析方法及步骤，计算求得和，并借助FLAC3D 有限差分软件计算水位骤降下岸坡的安全系数和临界破坏模式，计算结果见图5～6 所示。

图5 岸坡塑性应变云图Fig. 5 Bank slope plastic strain map

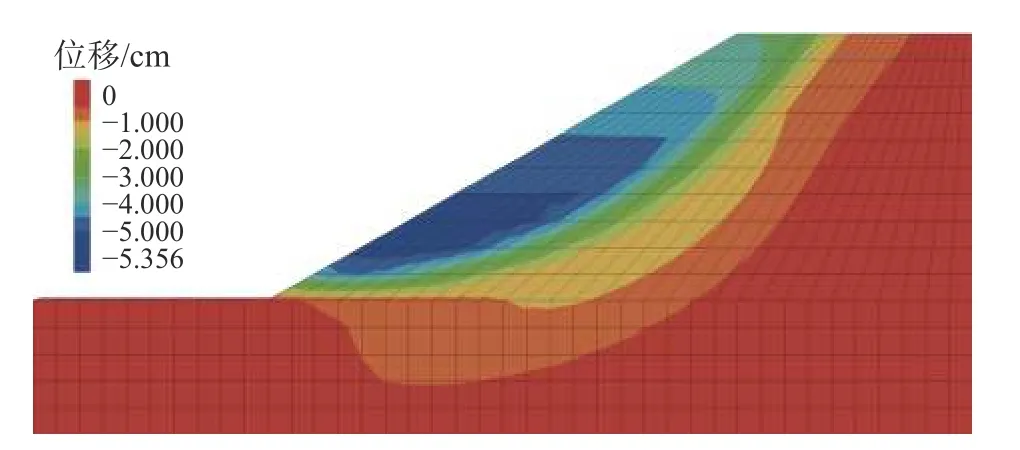
图6 水平方向位移云图Fig. 6 Horizontal displacement cloud map

图5 和6 表明，计算岸坡中塑形变形区已经贯通，坡脚处出现了较大水平方向位移，岸坡出现破坏，此时岸坡的安全系数为1.14；而文献[21]运用岸坡全局临界滑移场（GCSF）方法和GeoStudio 的SLOPE/W 模块方法计算该岸坡得到的安全系数为1.17 和1.18，结果相差为2.6%和3.5%，吻合较好。可见，本文所提出的简化分析方法具有一定的可行性。

为了进一步验证本文简化分析方法的可靠性，采用传统方法计算上述岸坡在库水位骤降作用下的安全系数，结果见表1。

表1 岸坡安全系数Tab. 1 Safety factors of bank slope

由表1 可见，本文简化方法与传统极限平衡方法相比，与Janbu 法相差最大(相差5.3%)，与不平衡推力法相差最小(相差1.8%)，平均相差3.5%，吻合较好。说明本文简化分析方法具有较好的可靠性。

3.2 非均质岸坡稳定性分析

为了进一步验证本文方法的有效性，参照文献[21]，选用如图7 所示的非均质黏土岸坡，在上述均质黏土岸坡的基础上，在距坡脚2～3 m 处存在厚度为1 m 的软弱夹层。软弱夹层力学参数c=0 kPa，γ=20.2 kN/m3，φ=10◦。采用本文所建立简化分析方法，计算水位骤降下软弱夹层的黏性岸坡安全系数和临界破坏模式，计算结果如图8～9 所示。

图7 非均质岸坡剖面(单位：m)Fig. 7 Heterogeneous bank slope profile (unit：m)

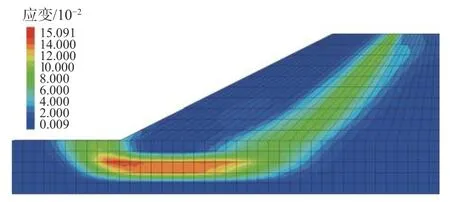
图8 岸坡塑性应变云图Fig. 8 Bank slope plastic strain diagram

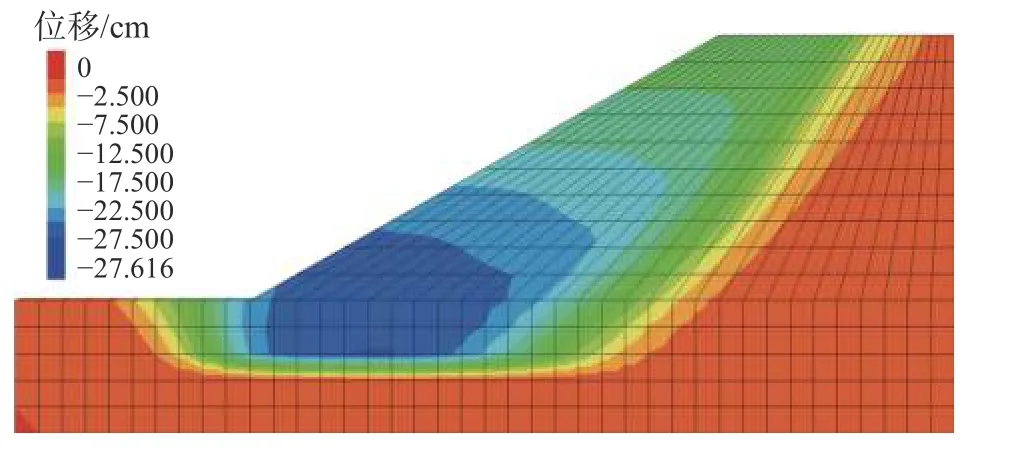
图9 水平方向位移云图Fig. 9 Horizontal displacement cloud map

图8 和9 表明，计算岸坡中塑形变形区已经贯通，软弱夹层出现了较大的塑性应变，坡脚至软弱夹层段水平方向出现了较大位移，岸坡出现破坏，此时岸坡的安全系数为0.99，与均质岸坡相比，安全系数显著降低；而文献[21]运用全局岸坡临界滑移场（GCSF）方法计算对该非均质岸坡进行分析得到的岸坡安全系数为0.96。两种方法计算得到的安全系数相差3.1%，吻合较好。可见，本文所建立的简化分析方法在计算非均质岸坡时也具有较好的可靠性和有效性。

4 结 语

针对水位骤降对岸坡稳定性的影响，通过分析考虑和不考虑渗透力作用下岸坡任一点的应力状态，建立了水位骤降影响下考虑渗透力作用的岸坡稳定性简化分析方法，得到如下几点结论：

（1）通过分析考虑和不考虑渗透力作用下岸坡任一点的应力状态，得到可将渗透力对岸坡稳定性影响简化为抗剪强度参数黏聚力降低的等效关系，并将此等效关系与强度折减法相结合，建立了简化计算模型，提出水位骤降影响下岸坡稳定性简化分析方法。

（2）针对均质岸坡，采用本文所建立的简化分析方法、岸坡全局临界滑移场（GCSF）方法、Geostudio 的Slope/W 模块方法及传统极限平衡分析方法计算水位骤降影响下均质岸坡稳定性，所得安全系数结果均吻合较好，表明采用该简化分析方法分析均质岸坡稳定性具有较好的可靠性。

（3）针对非均质岸坡，采用本文所建立简化分析方法与岸坡全局临界滑移场（GCSF）方法计算水位骤降影响下岸坡稳定性，所得安全系数结果吻合较好，表明采用本文所建立的简化分析方法分析非均质岸坡稳定性具有较好的适用性。