反坡正弦波形底板上F 型水跃水力特性的试验研究
李 桢,柳树摇,李 红
(1. 四川水利职业技术学院,四川 成都 611231;2. 四川省内江水利电力建筑勘察设计研究院有限公司,四川 内江 641000)
水跃消能作为一种传统消能方式在水利工程中得到了广泛应用。到目前为止水跃大致可以分为A、B、C、D、E 和F 型,在反坡上形成的水跃称为F 型水跃。Khader 等[1]认为反坡坡度大于−0.025 时,F 型水跃几乎不可控。McCorquodale 等[2]利用闸门进行尾水控制,研究了反坡坡度为−0.10、−0.167 和−0.20 的F 型水跃,并提出了共轭水深比、漩滚长度和能量损失的经验关系式。Abrishami 等[3]认为在弗劳德数小于9 时F 型水跃很难稳定。他们还发现,在相同的来流条件下,F 型水跃的共轭水深比和漩滚长度要小于平坡水跃。Pagliara 等[4]进行了一系列反坡上有槛和无槛F 型水跃的试验测试,使反坡坡度从0 变化到−0.20,得出槛的存在稳定了F 型水跃,并提出了预测F 型水跃漩滚长度和共轭水深比的一般方程。从以往的研究来看,F 型自由水跃的跃前水深对共轭水深比的影响、反坡对能量损失的影响可以忽略不计,且经典水跃的能量损失大于反坡上水跃[5-7]。针对粗糙底板上的水跃,也进行了大量的研究[8-16],粗糙底板的消力池减小了共轭水深和水跃长度,增加了消能率,最终可以降低消力池的造价。最近,Nikmehr 等[17-19]研究了反坡粗糙底板上的水跃水力特性,认为反坡粗糙底板对F 型水跃具有稳定作用并能有效减小水平漩滚长度、增加消能率。为了研究坡度和相对粗糙度对F 型水跃水力特性的影响,对具有较大坡度和弗劳德数的反坡正弦波形底板上的F 型水跃进行试验测试,并将特征参数的观测结果与平坡及反坡底板上的自由水跃进行对比分析。
1 试验装置和方法
所有试验均在宽0.50 m、深0.60 m、长10 m 的矩形有机玻璃水槽中进行。一台泵给水箱供水,并通过位于供水管路中的电磁流量计测量流量。来流从带有20 cm 长有压段的流线型闸板下进入反坡波形底板水槽,从而产生深度为y1的有压均匀流。反坡正弦波形底板的水平长度为1.0 m,底板包括6 个坡度i(−0.02、−0.03、−0.04、−0.05、−0.07 和−0.10)。反坡正弦波形底板安装在水槽内,波峰处于相同的倾斜水平。共有3 种波形板,正弦波形波长s 为68 mm,振幅t 分别为13、22 和34 mm。水平底板长3 m,与反坡底板相连。水槽采用平板闸门控制尾水深度。在所有试验中都对尾水闸门开度进行了调整,使得F 型水跃的起始处位于进水口位置(图1)。连接垂直压力计且外径为3.0 mm 的普朗特管用于测量边界层厚度δ(断面最大流速um所在的位置与底板之间的距离)和长度尺度b (当某点的时均流速u 等于其所在断面最大流速um的一半时所对应的位置与底板之间的距离)。采用三维声学多普勒测速仪(ADV)测量任意点的时均流速u,流速点沿水深的间距为1 cm。在水槽的垂直中心面上,测量了F 型水跃内部垂直于底板的若干条线上的流速沿水深分布。所有试验均使用精度为0.1 mm 的测针来测量F 型水跃的水面线。由于水面有波动,每个断面水深测量5 次并取平均值。用碎木屑来表现漩滚,漩滚末端到进水口的距离定义为漩滚长度Lr,漩滚末端处的水深为y2。共进行了57 次试验,试验主要参数见表1。波形板I 用于A、B、C、D、E、F 系列32 个试验,波形板II 用于G、H 系列13 个试验,波形板III 用于I、J 系列12 个试验。F 型水跃起始处弗劳德数Fr=v1/(gy1)0.5范围为5 到11,其中v1为水跃起始断面的平均流速(即进水口平均流速),g 为重力加速度。如果弗劳德数Fr 过低,则由于反坡的影响可能无法形成自由水跃,本试验并没有选取形成自由水跃的最小弗劳德数作为范围下限。雷诺数Re=v1y1/ν的范围为63 500 到139 446,其中ν 为运动黏性系数。3 个相对粗糙度t/y1分别为0.51、0.87 和1.34。主干试验(A2、B2、B4、B6、C5、D1、D3、D5、E1、F1、G4、H3、I3、J3)的测量数据包括水面线、水跃过程中几个剖面的速度,在其余的试验中,只进行了水面线和漩滚长度测量。

图1 波形床上的F 型水跃示意Fig. 1 Schematic sketch of F-type jumps on sinusoidal-corrugated beds
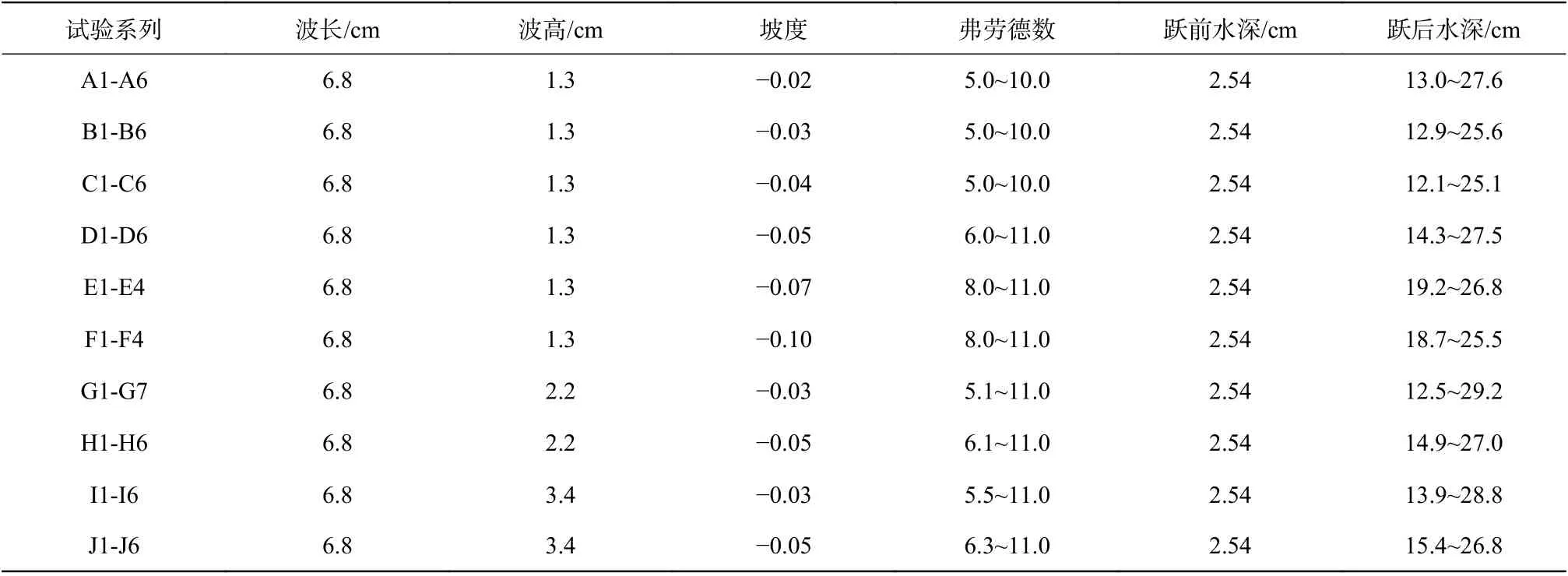
表1 试验主要参数Tab. 1 Main parameters of experiments
2 理论分析
对图2 中的控制体利用积分动量方程可以得到反坡正弦波形底板上的综合剪切应力Fτ:

图2 F 型水跃的定义和控制体Fig. 2 Defining diagram and control volume for the F-type jump
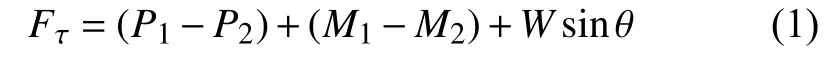
式中:P1、P2、M1和M2分别为跃前和跃后断面的压力和动量通量积分; θ 为反坡的角度(tanθ=−i);W 为单位宽度控制体中水的重量(图2)。利用连续性方程v1y1=v2y2,方程(1)可以简化成类似于Belanger方程的形式:

式中:Y 为共轭水深比;Gs为反坡水跃参数[2]。反坡水跃参数Gs为:
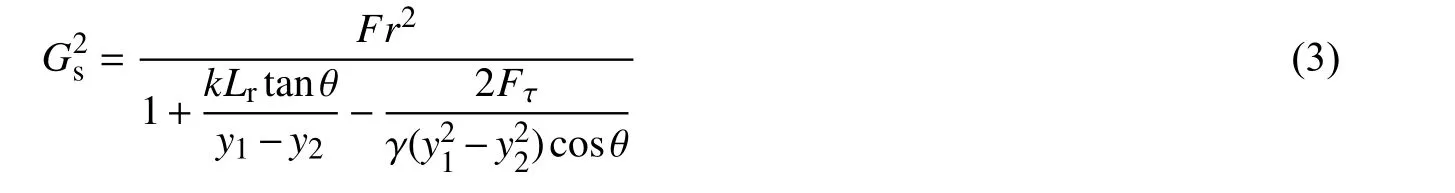
式中:γ 为水的重度;k 为形状系数。由式(2)和(3)得:

由Rajaratnam[20]引入的综合剪切力系数定义为ε=Fτ/(0.5λ),则式(4)可简化为如下形式:

3 试验结果与分析
3.1 共轭水深比
McCorquodale 等[2]定义形状系数k = SABCDE/SABDE,如图2 中所示ABCDE 的面积显然要大于梯形ABDE的面积。图3 显示k 值的范围从1.07 到1.24 不等,而在反坡光滑底板上F 型水跃的形状系数约为1.06[4]。从图3 来看弗劳德数、反坡坡度及相对粗糙度对形状系数均没有显著的影响。
如图4 所示,与平坡光滑底板和反坡光滑底板(i=−0.10)相比,反坡波形底板上F 型水跃的共轭深度比要小,这意味着反坡波形底板有助于稳定F 型水跃的位置。图5 为反坡水跃参数Gs与弗劳德数Fr 的变化关系。结果表明,反坡波形底板上F 型水跃的参数Gs小于平坡光滑底板及反坡(i=−0.10)光滑底板上的参数Gs[4]。通过试验确定了Gs与Fr 之间的关系,该关系是反坡坡度i 和相对粗糙度t/y1的函数。回归方程用计算式表示为:
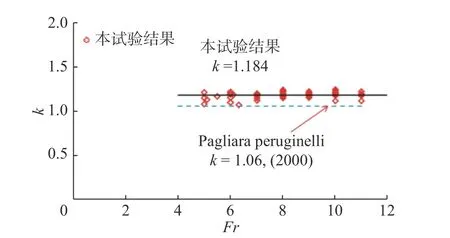
图3 形状系数k 与弗劳德数Fr 的关系Fig. 3 Relation of shape factor k and Froude number Fr

将式(6)代入式(2)可得共轭水深比的经验公式为:
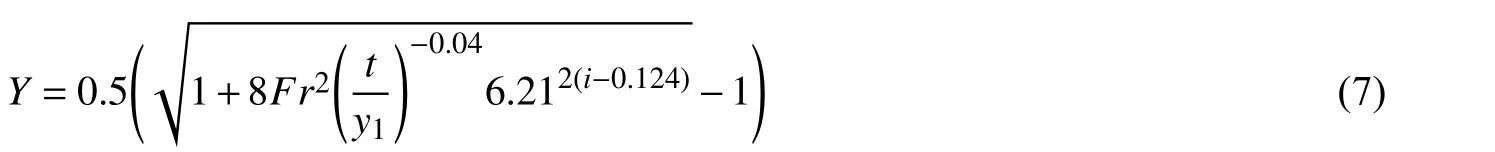
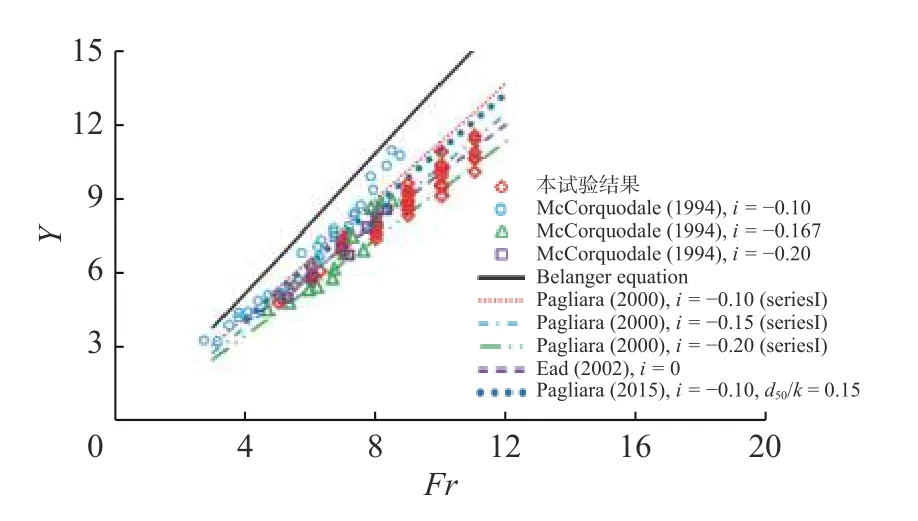
图4 共轭深度比Y 随Fr 的变化Fig. 4 Variation of the sequent depths ratio Y with Fr
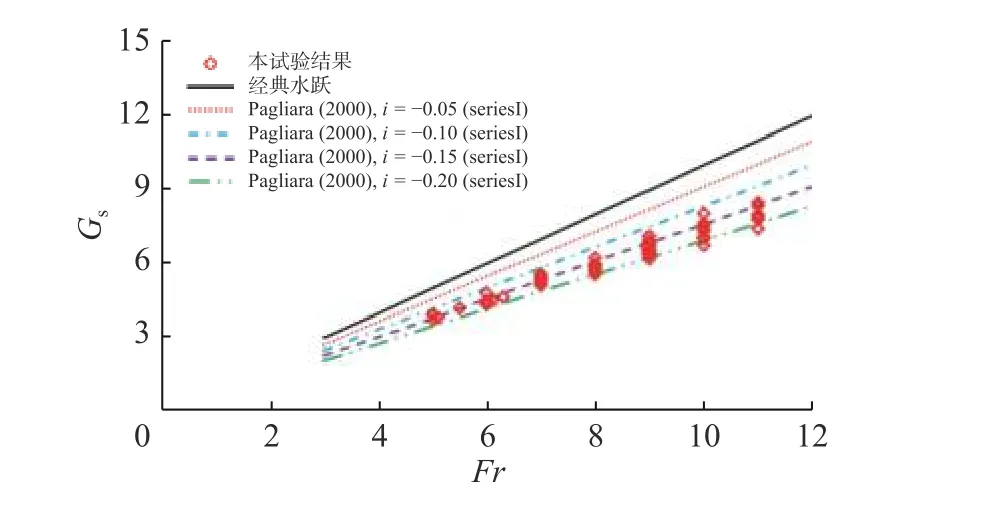
图5 反坡水跃参数Gs 与弗劳德数Fr 的关系Fig. 5 Relationship of adverse jump parameter Gs and Froude number Fr
3.2 漩滚长度
漩滚长度Lr的观测结果如图6 所示。可见,反坡波形底板上F 型水跃的漩滚长度Lr/y1小于反坡光滑底板的(i=−0.167)[2],比平坡光滑底板上的(i=0)减小约48%~62%[21]。这表明,反坡波形底板能够有效地减少F 型水跃的漩滚长度,并且粗糙底板造成的阻力是漩滚长度减小的主要原因,但其对相对粗糙度的大小并不十分敏感。根据目前的试验结果,得到反坡波形底板上F 型水跃漩滚长度Lr的经验式为:

3.3 流速分布
为了验证F 型水跃流速分布的相似性,以断面最大速度um为速度尺度,测点流速u 等于最大流速一半的位置与底板线的距离b 为长度尺度,这些尺度曾被Wu 等[22]使用。图7 显示了主干试验流速分布的相似性。从图7 可以看出,速度分布并不完全相似,反坡坡度i 和相对粗糙度t/y1一定程度上影响了速度分布的相似性,与经典壁面射流的轮廓有些不同。当y/b≤0.2 时,u/um小于经典壁面射流的值;当0.2<y/b≤1.0 时,u/um大于经典壁面射流的值;而当y/b>1.0 时,u/um小于经典壁面射流的值,并且u/um=1.0 时,y/b 大于经典壁面射流的值,这说明反坡波形底板不仅可以有效减小共轭水深比和漩滚长度,而且可以改善流速分布,使断面最大流速出现的位置更加远离底板,减轻对底板的冲刷。结果还表明,当底板的相对粗糙度t/y1恒定时,沿流向的剖面速度分布基本相似,且流速分布对相对粗糙度比坡度更敏感。
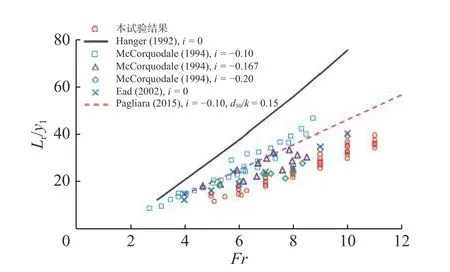
图6 漩滚长度Lr/y1 随Fr 的变化Fig. 6 Variation of the roller length Lr/y1 with Fr
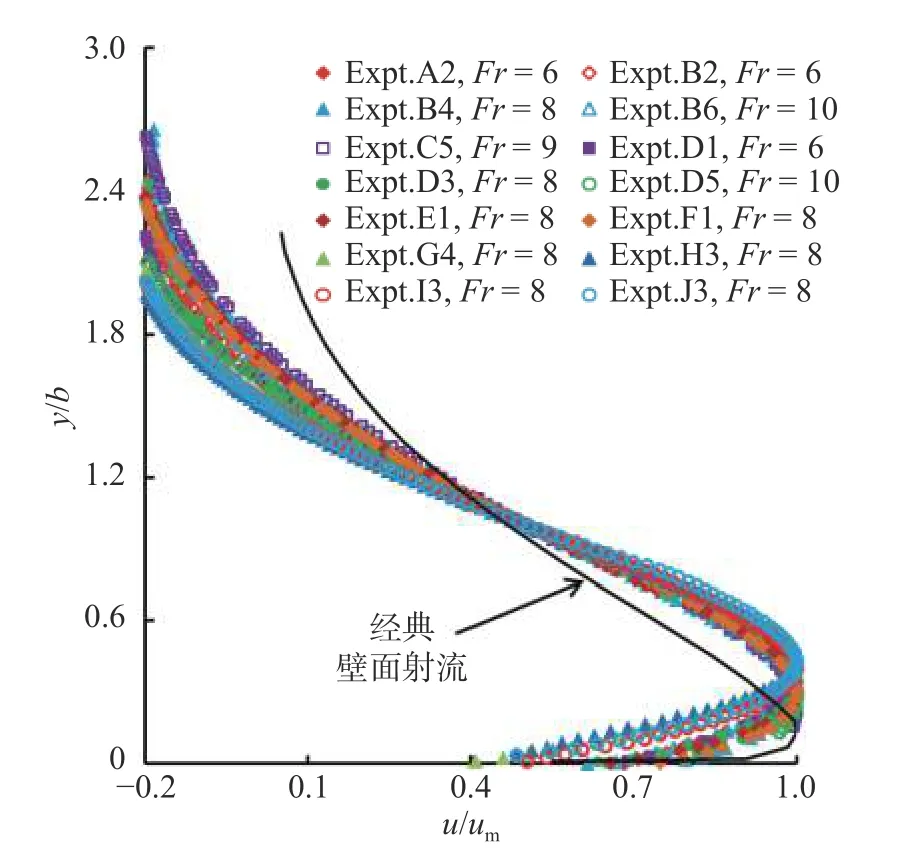
图7 沿流向剖面速度的相似性Fig. 7 Forward-flow similarity of velocity profiles
反坡波形底板能够改善流速分布,因此有必要对F 型水跃流速分布的均匀性进行讨论。动量修正系数β 与断面速度分布的均匀性密切相关,动量修正系数越接近1.0,断面速度分布越均匀。
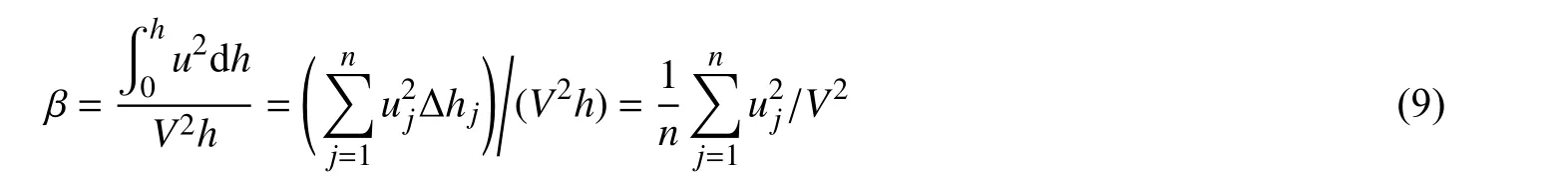
式中:V 为断面平均流速;h 为测量断面水深;沿断面水深测点序号依次为1, 2, 3, ···, n;uj为j 点处的时均流速;由于流速测量点沿水深的间距相等,则有Δhj=h/n。图8 为动量修正系数沿流向的变化情况。试验结果表明,动量修正系数随着F 型水跃的发展在x/Lr≤0.4 的范围内沿程增加,而在0.4<x/Lr≤1.2 的范围内沿程减小,在x/Lr>1.2 的范围内,基本接近1.0,流速分布近似均匀。在x=0.4Lr断面附近流速分布最不均匀,这是由于靠近漩滚中心的水流剪切作用较强,紊动剧烈,因此流速分布极不均匀。
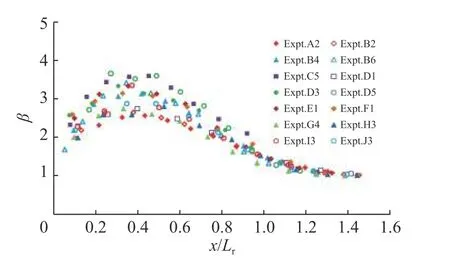
图8 动量修正系数β 随x/Lr 的变化Fig. 8 Variation of β with x/Lr
由于当u/um=1.0 时y/b 大于经典壁面射流的值,因此有必要讨论最大流速的衰减特性。图9 为um/v1随x/L 的变化,其中L 为um=0.5v1时距离水跃起始处的纵向距离。结果显示其最大流速的衰减与平坡光滑底板上自由水跃的最大流速衰减略有不同[22]。当x/L≤1.0 时,衰减几乎与壁面射流衰减曲线重合,且衰减速度快于平坡光滑底板上的自由水跃;而当x/L>1.0 时,观测结果介于自由水跃与壁面射流曲线之间,并且衰减速度略慢于自由水跃。从图10 可以看出,与平坡波形底板上的自由水跃相比,反坡波形底板上F 型水跃的特征长度尺度L 减小约10%~30%,这表明反坡可以显著减小水跃的沿流向特征长度,漩滚长度的试验结果也证明了这一点。根据目前观测结果描述长度L 的经验式为:

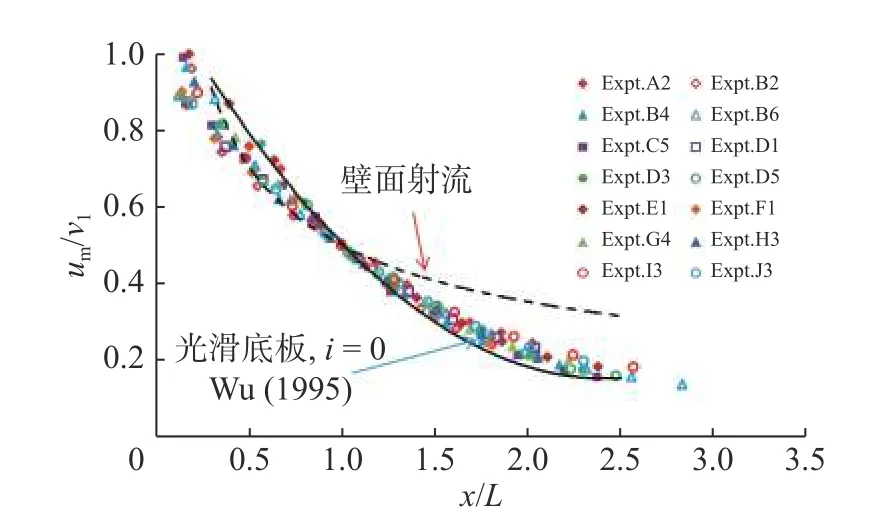
图9 最大流速um/v1 随x/L 的变化Fig. 9 Variation of maximum velocity um/v1 with x/L
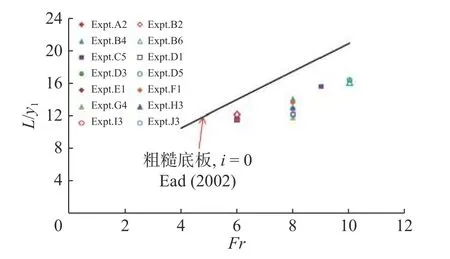
图10 长度尺度L 随Fr 的变化Fig. 10 Variation of length scale L with Fr
从图11(a)可以看出,对于反坡波形底板上的F 型水跃,沿水深长度尺度b 比平坡光滑底板上自由水跃的长度尺度沿程增长更快。目前的观测结果大致位于平坡光滑底板与平坡波形底板上自由水跃所得结果之间。由图11(b)可知,相对粗糙度对边界层厚度δ 的发展具有较显著的影响。观测结果显示,相对粗糙度t/y1=1.34 时的边界层厚度介于t/y1=0.51 和t/y1=0.87 时的边界层厚度之间,这说明边界层厚度并不是随着相对粗糙度的增加而增加,相对粗糙度较大时反而阻碍了边界层的发展。结果显示反坡波形底板上相对粗糙度t/y1=0.51 时相对边界层厚度δ/b 约等于0.31,而t/y1=0.87 和t/y1=1.34 时相对边界层厚度δ/b 约等于0.41。值得一提的是对于经典壁面射流δ/b 约等于0.16,而对于平坡波形底板δ/b 约等于0.45[12]。这说明相对边界层厚度δ/b 受相对粗糙度以及反坡坡度的共同影响。
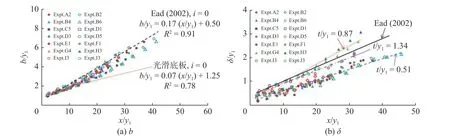
图11 长度尺度b 和δ 随x/y1 的变化Fig. 11 Variation of b and δ with x/y1
3.4 壁面剪切应力
前人研究认为粗糙底板上水跃下游深度y2较小的主要原因是底板壁面剪切应力的增加[12]。由式(5)可计算得到与反坡波形底板所对应的综合剪切应力系数ε 的值。如图12 所示,反坡波形底板上综合剪切应力系数ε 大约是其在平坡波形底板上的1.0~1.6 倍,并且大约是其在平坡光滑底板上的10~16 倍[12]。值得注意的是,目前的结果大约是其在坡度为i=−0.2光滑底板上的1.0~1.6 倍[2]。这说明底板相对粗糙度对综合剪切应力系数有较为显著的影响,而坡度的影响作用次之,总体而言,相对粗糙度和反坡坡度都能增加综合剪切应力系数。
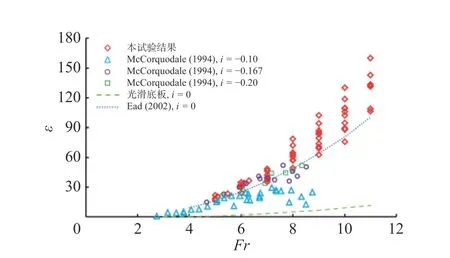
图12 壁面切应力系数ε 随Fr 的变化Fig. 12 Variation of shear force coefficient ε with Fr
3.5 能量损失
水力坡度是沿流向单位距离的水头损失。水力坡度可定义为式J=(E2−E1)/Lr,E1和E2分别为F 型水跃跃前和跃后断面的总水头。图13 为水力坡度J 随Fr 的变化。从目前的试验结果来看,坡波形底板上F 型水跃的水力坡度大约是其在平坡波形底板上的1.0~1.6 倍[12],并且大约是其在平坡光滑底板上的1.7~2.5 倍[23],同时比其在坡度为i=−0.1 光滑底板上的要大[2]。反坡波形底板不仅使其F 型水跃漩滚长度减少而且单位距离内的水头损失也较大,这说明反坡波形底板能够使F 型水跃在短距离内快速消能。根据目前观测结果描述水力坡度J 的经验式为:

反坡波形底板上F 型水跃的相对能量损失可定义为η=(E2−E1)/E1。如图14 所示,反坡波形底板上F 型水跃的相对能量损失比平坡光滑底板上的自由水跃增加约5%~20%[23],而且比其坡度i=−0.1 光滑底板上要大[2]。试验结果显示,其与平坡波形底板上的自由水跃的相对能量损失基本吻合[12],这也印证了前人的结论,反坡对能量损失的影响可以忽略不计。
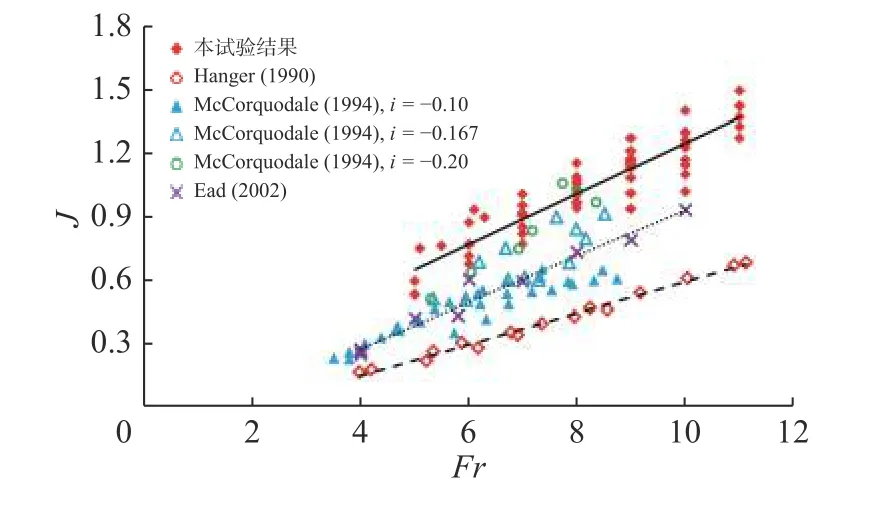
图13 水力坡度J 随Fr 的变化Fig. 13 Variation of hydraulic slope J with Fr
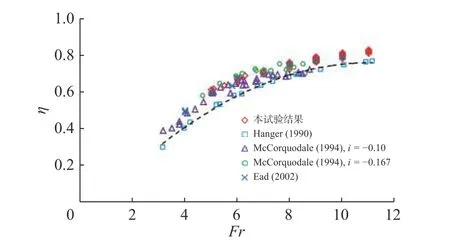
图14 相对能量损失η 随Fr 的变化Fig. 14 Variation of the relative energy loss η with Fr
4 结 语
本文主要研究了反坡正弦波形底板的坡度与相对粗糙度对F 型自由水跃水力特性的影响。基于弗劳德数从5~11 的变化范围、相对粗糙度从0.51~1.34、反坡坡度从−0.02~−0.10 的一系列试验结果,得出以下结论:(1)在所有的试验中,F 型水跃形状系数的范围为1.07~1.24。(2)反坡波形底板有助于稳定F 型水跃的位置,并能有效减小F 型水跃的滚筒长度和共轭水深比。(3)坡度和相对粗糙度影响F 型水跃剖面速度分布的相似性以及沿水深长度尺度和边界层厚度等的发展。(4)在距离漩滚长度40%处,断面速度分布最不均匀;在距离水跃起始处1.2 倍的漩滚长度后,断面动量修正系数基本上都接近1.0,断面流速分布均匀。(5)反坡波形底板的综合剪切力系数是平坡光滑底板的10~16 倍,增加了沿流向单位长度的消能率,因此比较适用于短距离快速消能。

