基于神经网络的体视PIV空间标定模型

窦建宇，潘翀,2,*

1. 北京航空航天大学 流体力学教育部重点实验室，北京 100083 2.北京航空航天大学 宁波创新研究院 先进飞行器与空天动力创新研究中心，宁波 315800

体视粒子图像测速(Stereo Particle Image Velocimetry, SPIV)是在二维(2D)PIV技术的基础上发展起来的一种使用2台相机测量激光照射平面(2D)内流体三分量速度场(3C)的技术，使用该技术可以获得待测平面内的2D3C速度场[1]。SPIV测量的关键之一就是建立多台相机成像的二维像素空间到三维物理空间的映射[2]。建立这个映射的过程叫做空间标定，具体过程是：通过几何尺寸和空间位置已知的标定板获得标定特征点在物理空间和像素空间上的坐标对，再选取合适的标定模型(也称映射函数)来描述两者之间的映射关系，通过最小二乘法来获取标定模型中的待定系数，从而建立完整的映射关系。其中，标定模型形式的选择对标定精度有较大的影响，常用的标定模型包括小孔模型或多项式模型[3-5]。

小孔模型是根据小孔光学成像原理建立的理想模型。虽然小孔模型的物理意义清晰，但也存在一些缺点，如：需要额外的算法来处理相机拍摄时的畸变[6]，拟合过程相对复杂，拓展到多个相机进行联合标定时算法的复杂度较高等[4]。

多项式模型通过多项式函数直接进行像素空间坐标与物理空间坐标之间的映射。相比于小孔成像模型，多项式模型在数学上更加简单[7]；同时，多项式模型是唯象的全局拟合，可以在一定程度上处理相机畸变。但是，为精确模拟相机镜头产生的径向畸变和切向畸变，多项式通常需要达到六阶[8]，但SPIV常用的多项式标定函数往往只取到二阶或三阶，因此对相机畸变的处理能力有限[9]。

除此之外，神经网络也被应用于相机标定。1998年Yoo和Lee提出了神经网络直接标定法[10]，使用神经网络建立泛化的映射关系，对于处理大畸变场景表现出较好的效果。现有研究集中于神经网络模型在大相机畸变场景下的精度[11]、神经网络模型在有噪声情况下的标定精度和神经网络模型的训练方式[10]等的研究。但鲜有针对SPIV实验场景下的空间标定模型研究，也缺乏对标定模型抑制输入误差能力的研究。本文使用仿真方法，研究空间标定过程中的输入性误差对小孔模型和多项式模型标定精度的影响和误差传播特性，在此基础上结合神经网络的高阶拟合能力和联合标定能力，搭建可替代小孔模型/多项式模型的神经网络空间标定模型，进一步通过对比研究证实本文所发展的神经网络模型对于输入性误差有更好的抑制能力，并且可以更好地适应大畸变等极端测量条件。

1 空间标定的误差传播

1.1 标定误差

从产生方式上分，SPIV的标定误差有两大来源，第1类是输入性误差，即输入到标定模型中的标定数据中存在的误差，这部分误差与标定模型无关，是标定时引入的误差[12]；第2类是缺陷性误差，即由标定模型在某方面的先天缺陷所产生的误差，比如由于小孔模型的理想化处理导致其无法处理相机畸变而产生的标定误差，是一种系统性偏差[13]。

本文研究的输入性误差是指提取标定点像素空间坐标时产生的特征点识别误差。标定点在像素空间的位置通常使用图像处理算法自动化识别[14-15]。尽管可以使用亚像素插值等手段来提高精度[16]，但是光照角度、光照强度、感光芯片的随机白噪声等因素都会影响到算法的识别精度，因此图像处理算法识别到的角点距离真实角点往往存在一定的偏差。标定点识别误差如图1所示。在实际标定中，标定点识别误差基本在1 pixel以下。由于具有随机性，基于单相机的小孔模型和多项式模型对这类误差都没有很好的处理办法，实验中常常通过改善光照条件和提高相机分辨率等方式减小这部分误差。而采用多相机联合标定的方法，可以在统计意义上一定程度地抵消这一随机误差。

图1 标定点识别误差示意图Fig.1 Illustration of calibration point identification error

本文探讨的缺陷性误差主要指畸变产生的误差。光学系统往往带有视场畸变，其本质是在某些区域(一般是远离成像中心点的区域)的成像具有明显的非线性特性。畸变会导致成像扭曲变形，小孔模型和多项式模型在标定时都会因为无法拟合成像中的高阶部分而产生误差[17]。此外，双目/多目系统中相机光轴和测试平面法线方向存在夹角也会带来缺陷性误差。对于两台相机在同侧对称布置的SPIV构型，当相机夹角较小时，测试平面法线方向上的定位精度较差；而当夹角较大时，测试平面内的定位精度较差[17-19]。

1.2 误差传播及误差衰减系数

本文定义一无量纲量，即误差衰减系数，来描述输入性误差通过标定模型的传播特性，其定义为

a=10×lg(ein/eout)

(1)

2 SPIV的空间标定方法

如前文所述，建立从像素空间到现实空间的映射的过程叫做空间标定，其根本是建立一个数学模型，将像素空间位置对应到现实空间中。

相机标定的过程通常需要将相机调整至实验状态(包括空间位置和姿态等外部参数和相机光圈、焦距等内部参数)，在待实验平面处放置标定靶，标定靶上有精确打印的空间坐标已知的特征点阵(通常是圆点或者棋格板的角点)，使用相机拍摄标定板，通过数值图像处理技术提取图片中特征点在像素空间的坐标，选取合适的映射关系(如多项式模型或小孔模型)，将特征点阵在物理空间中的坐标和像素空间中的坐标进行配对，使用最小二乘拟合出映射函数中的待定系数，即可得到针对特定实验状态的映射函数[18, 20]。为了获得对垂直于标定靶平面的纵深方向的准确标定，还需要在垂直实验平面的方向移动标定靶，拍摄一系列纵向位置改变的标定靶图像，再对各个纵向位置的标定平面分别拟合出映射关系[21]。

常用的2种标定数学模型是小孔模型和多项式模型，下面分别简要介绍。

2.1 小孔模型

小孔模型是根据小孔成像原理建立的一套模型。在该模型中，将相机成像的过程理想化为小孔成像。小孔成像原理示意图如图2所示。从物理实现来看，通常将成像过程分解为3个部分[4]：将待成像物体刚体变换到焦平面；将焦平面上的物体投影到成像平面，即传感器处；最后将成像平面的信息采样到每一个像素点上。

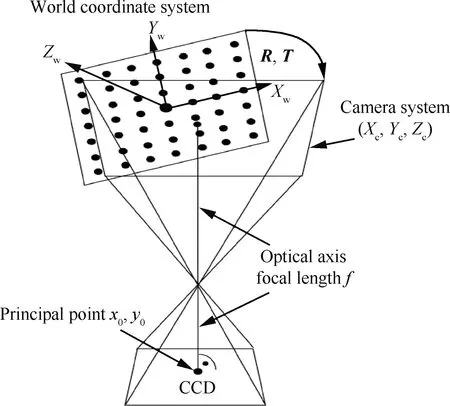
图2 小孔成像模型示意图[4]Fig.2 Schematic diagram of pinhole imaging model[4]

通常将小孔模型涉及到的参数分为内参和外参两组，前者是相机内部的参数，与焦距、光圈、感光芯片的尺寸等有关[22]，而后者与相机在拍摄时的空间位置和角度有关。一个典型的小孔模型可表达为

(2)

式中：x和y为像素空间坐标；Xw、Yw、Zw为现实空间坐标；Zc为现实空间做刚体变换后坐标原点在成像平面坐标系中的Z轴坐标；等式右侧前2个矩阵为内参矩阵，dx和dy为感光芯片上单个像素的物理尺寸，x0和y0为感光芯片中心点位置，f为相机的等效焦距；第3个矩阵为外参矩阵，R为旋转矩阵，T为平移向量。

2.2 多项式模型

(3)

式中：ai、bi和ci为待拟合系数,i=0,1,…,9。另外，有些SPIV的标定算法并不通过多项式表达沿激光平面法线方向的Z分量，而是通过三角定位来处理Z分量[9]。

3 神经网络模型

3.1 神经网络原理

神经网络是一类模仿神经系统学习过程的算法。使用神经网络取代传统空间标定模型的优势在于以下几个方面：① 空间标定过程的输入输出关系简单且确定，适合使用神经网络进行描述；② 神 经网络通常比给定阶数的多项式具有更强的高阶拟合能力，因此便于处理高畸变、非均匀放大率的场景[23]；③ 神经网络具有联合标定能力，即其输出结果可以同时受到所有输入信息的影响，因此易于扩展到多相机联合标定。本文中的神经网络的使用方法与其他模型相同。神经网络也有其自身的缺陷，比如在建立模型的阶段，神经网络的训练时间较长，本文中神经网络训练需要20 min，而多项式模型的建立仅需要0.3 s；在使用标定结果对1 000个点进行三维重构时，神经网络耗时12.743 9 s，三阶多项式耗时0.036 2 s。

本文选用级联误差反向传播神经网络(BP神经网络)来建立SPIV空间标定模型，其原因是BP神经网络适用于空间标定这类高阶函数拟合问题[22]，同时其发展也相对成熟，通过调整网络节点数量、隐含层数量及训练方法可以方便地优化其在空间标定中的性能[24]。

图3 SPIV标定神经网络模型示意图Fig.3 Schematic diagram of neural network model for SPIV calibration

为了寻找合适的神经网络参数，本文针对神经网络的隐含层数、节点数和训练方法等进行了对比测试。神经网络的参数尤其是其层数和节点数具有随意性，并且暂时只有经验公式可供参考，对各个参数逐一测试时间成本过大。考虑到影响神经网络结果的一组矛盾分别是过拟合和欠拟合，过拟合指的是神经网络过于复杂，过度学习了样本的特点，以至于把其中的误差当成了样本规律；欠拟合指的是神经网络学习能力不足，以至于不能完全学习样本的规律[25]。所以本文尝试找出抗过拟合能力较强的训练方式以避免过拟合，随后选择一略大的网络层数和网络节点数避免欠拟合。

3.2 训练方法及网络复杂程度选择

神经网络的训练方法指的是在训练过程中利用样本更新权值的方法。不同的训练方法对于神经网络性能的影响比较大。对于各种训练方法的具体原理已经超出本文的范围，将不再赘述。本文使用仿真测试的方法，对比了LM(Levenberg-Marquardt)训练法、贝叶斯正则化方法和动量训练法在不同网络复杂程度下的表现。仿真实验的技术细节在第4节给出。

一般认为LM法收敛速度较快，贝叶斯方法抗过拟合能力强，动量法可以避免局部最优问题。对比计算中分别选择具有1～4层隐含层的神经网络。增加隐含层数可以较大地提高神经网络的高阶拟合能力，即对于相同总节点数的神经网络，拥有更多层数的网络拥有更强的高阶拟合能力，同时也更容易产生过拟合。但使用更多层的神经网络有利于减少总的节点数，以减小计算量。对比时，本文设定的训练结束条件为计算达到50 000步或者计算时间超过20 min或者代价函数梯度小于10-6。在此情况下，影响计算精度的几个因素分别是收敛速度、网络复杂程度和训练方法抗过拟合能力。表1给出3种训练方法在不同隐含层和节点数下，在第4节给出的缺省标定场景下的空间标定误差，空间标定误差的计算方法在4.1节中具体给出。从表1可见，动量法的误差始终较大，LM法和贝叶斯正则化方法误差都是随着隐含层层数的增加先减后增，在三层五节点时达到最小误差，其中贝叶斯正则化方法得到的误差更小。因此，本文选用三层五节点网络，并使用贝叶斯正则化方法进行训练。

表1 隐含层数、节点数和训练方法对神经网络标定误差的影响

4 仿真实验

为了得到标定特征点在像素空间和物理空间的真实位置，以及定量控制输入性误差，本文使用仿真实验而非实物实验来对比研究各种标定模型的误差传递特性，从而证明神经网络标定的优势。

4.1 虚拟仿真方法

本文使用基于小孔模型的空间投影算法将物理空间中的标定点阵投影至左右2个相机的像素空间，从而形成训练数据集和测试数据集。为尽可能还原真实情景，使用的投影算法考虑了相机的焦距、分辨率、传感器单元尺寸等相机内部参数[26]，以及标定板和相机的空间位置关系等外部参数，同时还模拟了相机镜头的畸变(包含径向畸变和切向畸变)和特征点识别误差。特征点识别误差通过在特征点的像素空间坐标位置上叠加高斯白噪声来模拟，用高斯白噪声的标准差来定量刻画特征点识别误差的强度。

在仿真模拟中，标定靶上的特征点规则排列，在标靶平面内包含20×20个点，物理空间中标定靶在法线方向上等间距移动10次，从而形成20×20×10的训练集点阵。测试集为标定靶移动所覆盖的三维空间中随机分布的20 000个测试点。典型的训练集截面和测试集截面如图4所示。

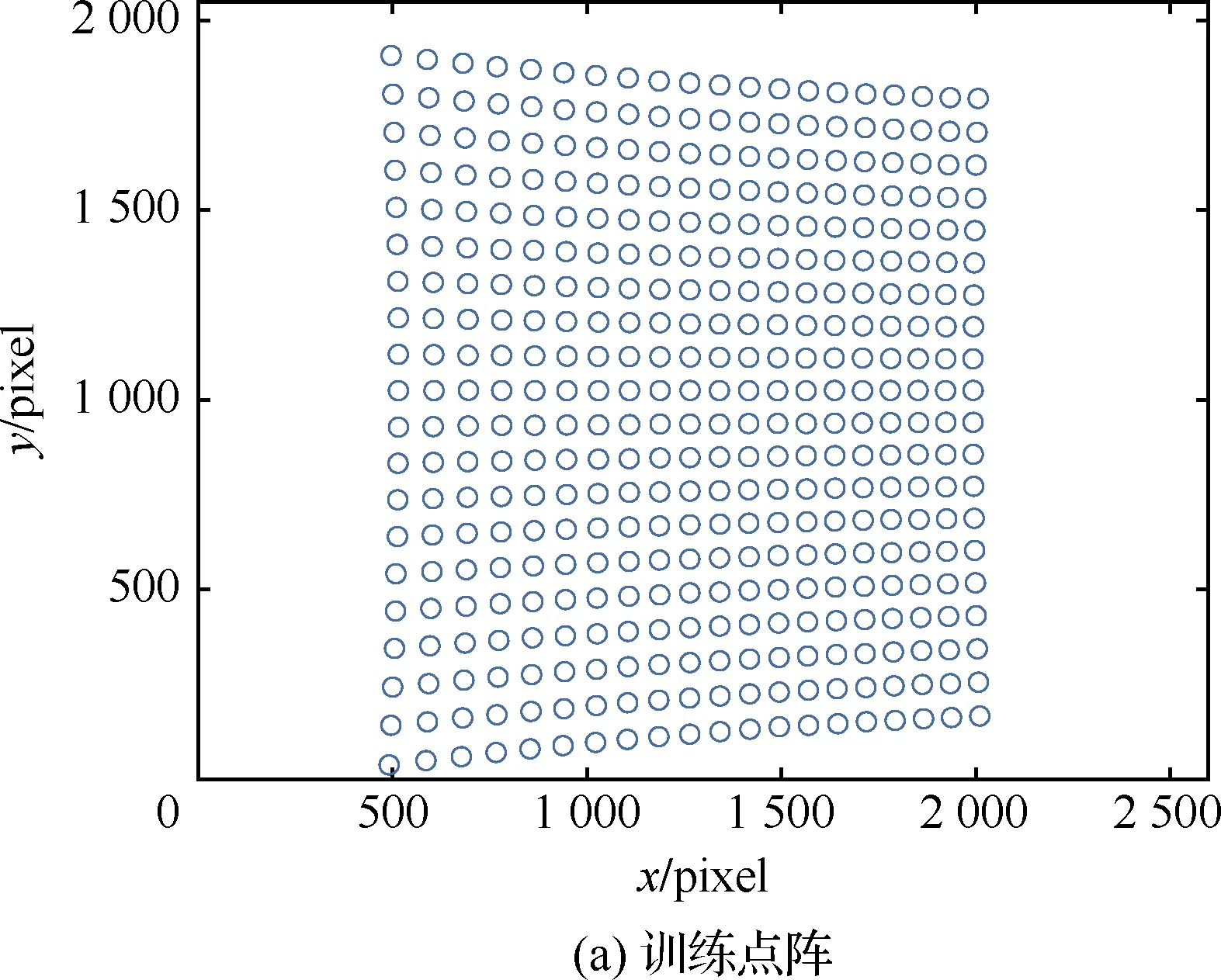
图4 训练点阵及测试点阵示意图Fig.4 Illustration of slice of training dot array and testing dot array

对比测试过程如下：首先使用同一组训练集训练神经网络、多项式模型及小孔模型，然后使用同一组测试集计算各模型的输出误差，输出误差定义为每个测试点的模型输出(ξ)与其真实物理空间坐标之差的绝对值，使用测试集中所有点的输出误差(包含X、Y、Z这3个分量)的L2范数作为此次测试的误差量度。为了保证实验结果的可靠性，对于每一个工况，都进行30次重复实验，取平均值作为最终结果。

4.2～4.4节中模拟的基准实验工况为：相机至拍摄平面0.75 m，两相机对称布置在实验平面同侧，无特殊说明时相机间夹角为60°，待测量平面(激光片光照明平面)的厚度为2 mm；相机的等效焦距50 mm，分辨率为2 594 pixel×2 048 pixel，像素单元为正方形、单个像素单元边长为4.8 μm。后续测试将讨论联合标定、特征点识别误差和相机畸变对标定精度的影响。

4.2 联合标定对标定精度的影响

为了证明联合标定可以在一定程度上增强标定模型对于输入误差的抑制能力，首先对比使用和未使用联合标定的神经网络在抑制误差传播上的性能表现。使用联合标定时，神经网络的输入为左右相机的4个坐标(以下简称双目标定)；未使用联合标定时，需要对左右2个相机分别训练一套神经网络(以下简称单目标定)。

图5给出有/无联合标定能力的神经网络的误差衰减系数a随输入误差的变化。如前所述，使用像素平面上特征点位置的高斯白噪声来模拟输入误差(特征点识别误差)，所模拟的输入误差的标准差范围为0.012 5～3.2 pixel。需要注意的是，真实的标定实验中，特征点识别误差一般不超过1 pixel。从图中可以看出，单目标定时(无联合标定)，神经网络在输入误差较小(<1 pixel)时无法抑制误差传递(a<0)，但双目标定(有联合标定)可以在一个很大的输入误差范围内抑制误差传递。因此，下文中用到的神经网络标定将采用双目联合标定。遵循一般做法，多项式模型采用单目标定；此外，小孔模型无法采用双目联合标定。

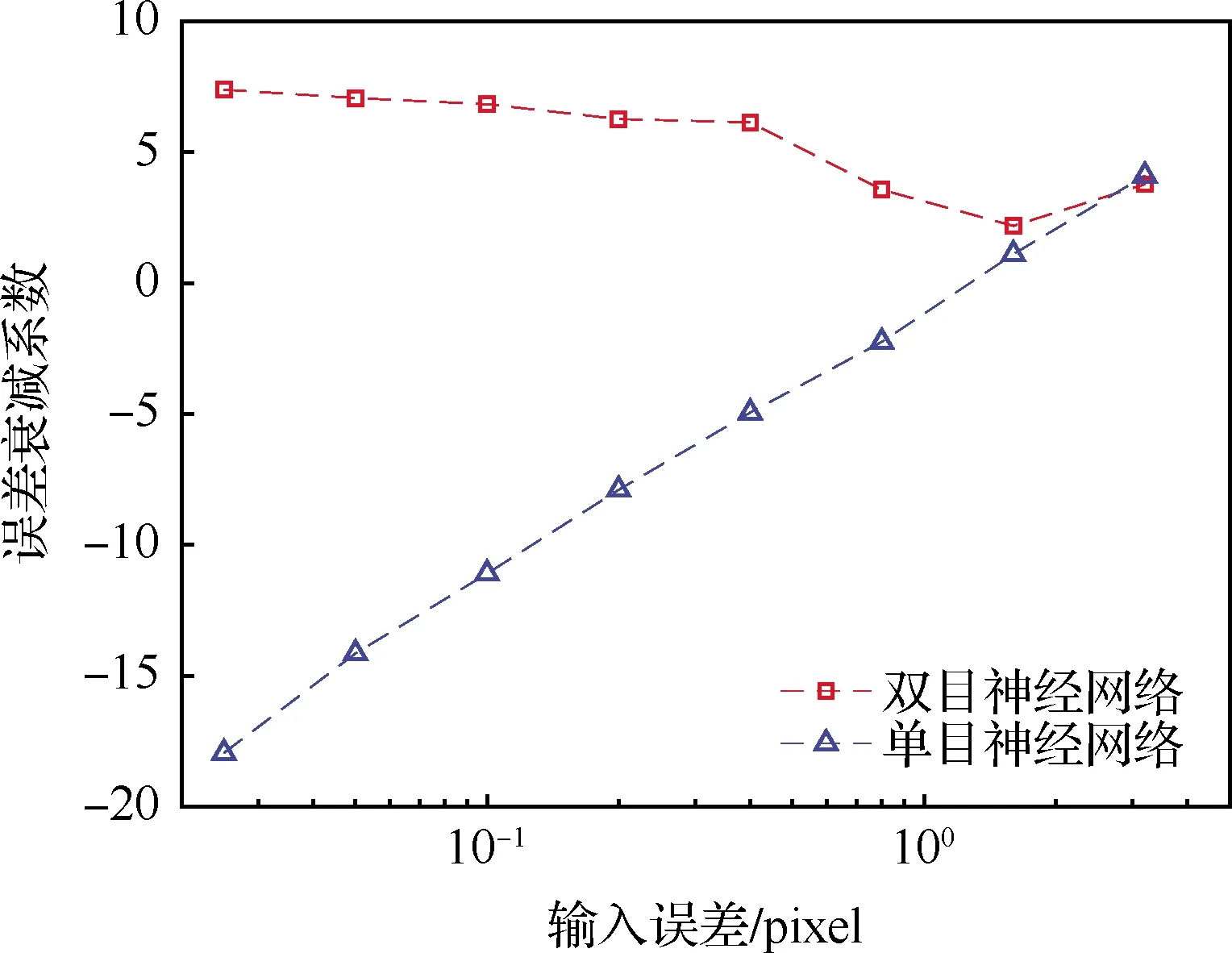
图5 联合标定能力对标定精度的影响Fig.5 Influence of joint calibration capability on calibration accuracy

4.3 特征点识别误差对标定精度的影响

标定模型对于输入误差的响应特性可以在一定程度上反映该模型的鲁棒性和高阶拟合能力。一般来说，高阶拟合能力和鲁棒性是相互制约的。本节在典型工况(相机等效焦距50 mm、相机夹角60°)下对比研究了4种标定模型(神经网络、三阶与二阶多项式和小孔模型)对输入误差的响应。仿真结果如图6所示。可见，神经网络模型和三阶多项式模型的性能优于二阶多项式和小孔模型，两者均能在很大的输入误差范围内抑制误差传递，且前者相对更优。而二阶多项式和小孔模型在输入误差较小(<1 pixel)时放大了误差(a<0)。

图6 输入误差对误差处理能力的影响Fig.6 Influence of input error on error processing ability

4.4 相机畸变对标定精度的影响

为减小相机畸变对标定的影响，在SPIV实验中应尽量避免使用小等效焦距的相机。如前所述，神经网络的高阶拟合能力较强，在处理具有高畸变的工况时应该具有更好的表现。本节研究相机畸变对标定模型精度的影响。在典型工况(60°相机夹角，输入误差标准差为0.4 pixel)下，相机具有固定的拍摄距离和畸变系数，等效焦距发生变动。因为畸变系数和等效焦距共同决定畸变大小，因此可以近似用等效焦距来表征畸变的大小。

图7给出误差衰减系数随相机等效焦距的变化曲线。所评估的4种模型中，神经网络仍然具有最好的表现，只在极短焦距时出现a<0的情况，且随着焦距的增大(畸变的减小)a数值趋于稳定。相比之下，三阶多项式也具有抑制误差传递的能力，但性能不及神经网络。

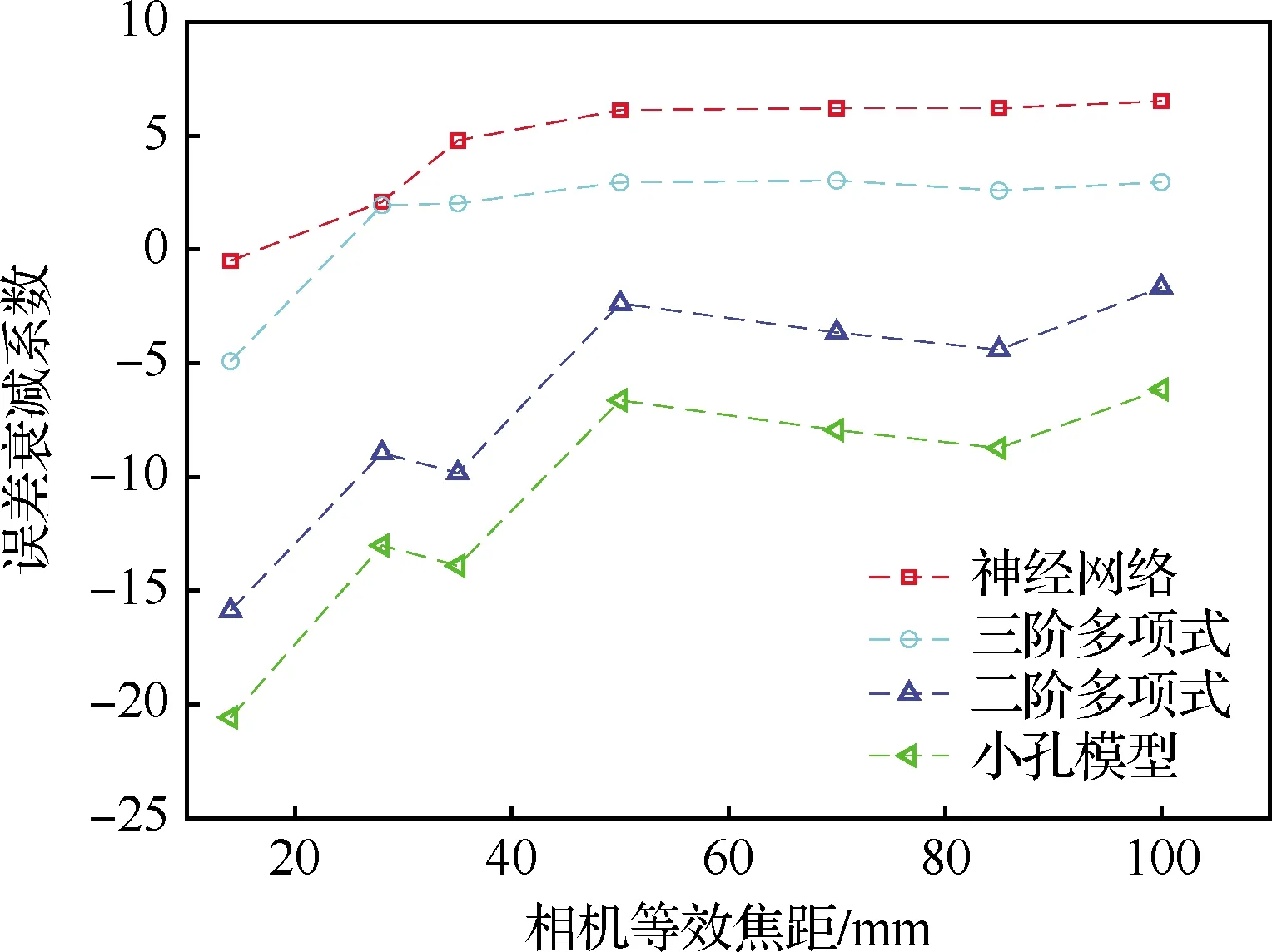
图7 相机畸变对误差处理能力的影响Fig.7 Influence of camera distortion on error processing ability

5 实验验证

为了验证仿真实验中的结论，本文针对神经网络、多项式模型和小孔模型进行了测试。实验中的输入误差未知，因此实验中使用绝对误差而非误差衰减系数作为衡量标准。

实验中使用2台海康威视的工业CCD相机(MV-CH050-10UM)，其分辨率为2 000 pixel×2 000 pixel， 相机与标定平面法线的夹角为3°，标定空间为170 mm×170 mm×1 mm。棋盘格标定板由高精度位移台定位，实验中一共拍摄10个标定平面，相邻标定平面的法向间距为0.1 mm。实验现场如图8所示。

图8 实验场景Fig.8 Experimental scene

空间定位的绝对误差如表2所示。绝对误差由4.1节 给出的方法来评估。从表中可见，神经网络标定模型相比于其他标定模型具有更高的定位精度。三阶多项式略优于二阶多项式，两者明显优于小孔模型。实验结果与仿真结果定性一致。

表2 4种空间标定模型的实测标定误差

6 结 论

本文针对SPIV两相机空间标定的误差产生和传播特性发展了一种基于神经网络的SPIV空间标定模型，使用仿真实验手段和实验测试证实：

1) 神经网络模型具备可扩展的联合标定能力，可通过随机误差相互补偿的方式有效抑制输入误差在标定-重构过程中的传播；而多项式模型和小孔模型在一般场景下均会放大输入误差。

2) 神经网络模型的高阶拟合能力使其尤其适合于大畸变场景。

3) 在常见的SPIV光学参数下，神经网络模型的空间定位误差仅为三阶多项式的1/4。

神经网络模型因其可扩展性，可以方便地使用更多相机开展联合标定，后续将尝试将神经网络模型用于层析PIV的三维空间标定。