蜂群对抗决策故障下的容错博弈控制

倪媛，杨浩，姜斌

南京航空航天大学 自动化学院，南京 210016

受自然界中生物集群行为的启发，蜂群无人机将大量低成本小型无人机整合形成一个整体，通过信息共享和分工合作执行复杂任务活动，如集群作战[1]、城市救援[2]、环境勘测[3]、防灾减灾[4]等，具有局部通信、分布式控制、动态自组织的特点。特别是对于大规模蜂群无人机，分簇结构有利于明确任务分工，实现组队协作，同时也能够减少网络管理开销、降低节点间干扰、提高网络容量[5]。

蜂群无人机的任务分配是蜂群应用的核心技术，旨在根据不同的蜂群任务类型、无人机数量、任务载荷情况等，对目标任务进行预先设定与统筹管理，进而优化蜂群无人机的应用效能。目前实现任务分配的方法主要为基于逻辑的自上而下式的规划，其数学模型复杂，对无人机数量敏感[6]。文献[7]介绍了两类离散化粒子群算法模型，可用于求解集群高维复杂离散优化问题；文献[8-9]均构建了混合整数线性规划模型，并对粒子群算法加以改进，从而加快粒子收敛速度，使任务分配模型适应大规模集群的需求。而基于集群智能涌现的自下而上式的任务规划，则是由无人机个体根据简单局部规则收集处理外界信息并与其他个体交互，更新自身状态，从而涌现出复杂有序的集体行为[10]，对于无人机数量庞大、信息不完全、高动态调整等环境下的群决策要求有着更强的适应性。

演化博弈论是生物进化与博弈论的有机结合，在描述解释蜂群行为的形成和演化方面有着重要意义。借助这一工具可以清楚地展现群体中个体的交互状态以及每个策略的演化趋势，进而确定系统可以到达的稳定状态。基于对稳定状态的研究可以得到影响任务分配的因素并提炼出相关的促进机制。因而，演化博弈论为解决任务分配问题提供了强有力的理论框架。文献[11]研究了基于演化博弈的多智能体系统的任务自组织分配；文献[12-13]同样采用演化博弈论这一工具研究了多机器人系统中的任务分配问题。

另一方面，故障会导致不期望的系统行为出现，互联网络系统的故障既会发生在单个智能体内部，也会出现在智能体之间的耦合机制[14-18]，文献[19]对该领域的研究进行了系统性的梳理和总结。现有的容错控制方法和技术大多对物理层面的故障进行补偿和修复，例如执行器、传感器等部位。

对于交互密切、存在大量协作关系、且个体成本较低的蜂群无人机，笔者认为相比较物理层故障，对群性能影响更大的是决策层面的故障。在对抗场景下，敌方运用电子战设备能够降低我方无线电电子设备的效能，削弱我方获取信息的能力，实施信息对抗以进行诱骗和干扰[20]，可能导致通讯指挥失灵、雷达迷盲、火炮和导弹武器失控等后果，这类故障属于意图明确的恶意故障，作用于决策层面而非物理机体。在基于博弈的任务场景中，文献[21]认为敌方可以直接影响我方某些个体的决策规则，进而改变群体行为；文献[22-23]研究了网络信息系统的安全问题，其中故障被认为是一类致力于破坏纳什均衡稳定性的攻击。目前，对于这类决策层面的故障和恶意攻击，已有部分研究对其进行检测和估计。文献[24]针对网络物理系统中的故障和外部攻击设计了集中式和分布式攻击检测与识别监视器。文献[25]从控制理论的角度概述了工业网络物理系统中安全控制和攻击检测的研究进展。文献[26]采用故障传播有向图及一致性理论，对蜂群无人机故障机理进行了研究。然而，针对决策层故障的容错博弈控制研究成果鲜有报道。

本文针对大规模分簇蜂群无人机的任务分配问题，考虑对抗场景下某些无人机由于受到敌方攻击或操控，决策规则遭到篡改进而导致群决策行为偏差的决策故障。首先，结合蜂群无人机分簇管理的结构特点，运用复制子动态这一演化博弈的典型方程对蜂群无人机和故障建模；然后，为补偿故障导致的群决策行为的偏差，对故障发生前后的均衡点的局部渐近稳定性及其吸引域进行分析，提出自容错条件和基于激励的簇间协同容错博弈控制方法。

1 模型建立

1.1 系统模型

考虑蜂群无人机的分簇结构，将其分为p≥2个簇进行管理，从各簇中重复且随机地选取两个无人机进行双人博弈。簇的交互关系采用文献[27]中的有向图G1≜(P,E)表示，其中P≜{1,2,…,p}为组成蜂群的所有无人机簇的集合，E为边集，顶点集对应于各个簇。〈w,v〉∈E，v,w∈P为由顶点w指向顶点v的边，表示簇v可以获得与簇w博弈而产生的收益。Nv≜{w|〈w,v〉∈E}为簇v的邻居集合。Lv≜{l|〈v,l〉∈E}为以簇v为邻居的簇l的集合。为保证蜂群无人机簇内的交互性以及簇间的互联性，要求任意v∈P均满足v∈Nv、v∈Lv且Nv-{v} ≠ ∅。

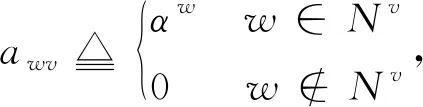
考虑蜂群无人机规模庞大，而无人机个体通信资源有限，为了合理利用资源并减小通信干扰，对于任意簇v，仅有簇v的邻居w∈Nv和以簇v为邻居的簇l∈Lv-{v}与其建立通信链路。因而可以采用无向图G2≜(P,E)，Ε≜{(w,v)|w∈Nv∪Lv,v,w∈P}表示蜂群无人机的通信拓扑。

蜂群无人机的任务分配问题研究如何将合适的任务分配给合适的无人机以实现理想的分工收益。基于文献[11]中三策略任务分配博弈模型，针对蜂群无人机的分簇结构，将决策模型推广到n元任务集合以及分簇网络结构的情形。现对n个任务进行分配，蜂群的任务集合S≜{1,2,…,n}，簇v的任务集合Sv⊆S。在演化矩阵博弈的理论框架下，博弈参与者的策略即无人机执行某项任务的决策是实现任务分配的核心，而博弈模型中的支付矩阵作为自主决策模块中的决策规则，决定了蜂群无人机的任务分配状态。在博弈过程中，无人机个体可以获得与其选择任务相对应的收益和协同收益。定义无人机独立执行任务i的收益为bi>0，协同收益dij≥0，后者代表执行任务i的无人机与执行任务j的无人机协作时获得的额外收益。以抢险救灾的应用背景为例，一方面，无人机通过侦察险情、运送物资、建立通信网络等行为获得任务回报，与此同时也需付出时间物力成本消耗，该差值构成了任务收益；另一方面，执行侦察任务与执行应急救援任务的无人机交互时，存在传递信息等合作行为，而即使是对于执行同一任务的无人机，往往合作的效益也大于“单打独斗”，有时还会存在分摊成本的情况。根据以上描述，〈w,v〉∈E对应的支付矩阵记为π[w,v]≜B[w,v]+D[w,v]，其中π[w,v]、B[w,v]和D[w,v]均为n阶方阵。

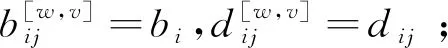
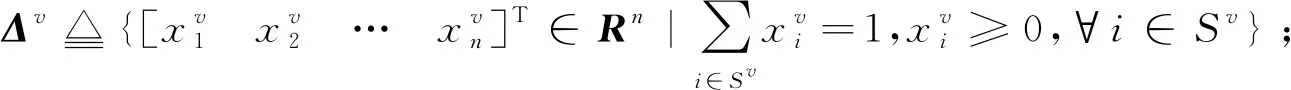
6)Θ为混合策略组合构成的空间，Θ≜×v∈PΔv；

8) intΘ为混合策略组合构成的空间内部，intΘ≜×v∈PintΔv；

基于以上定义和符号，蜂群无人机的任务分配动态可以用多群体复制子动态方程描述：

(1)

定义1意味着当蜂群的初始任务分配状态位于吸引域Ω内时，其任务分工会自发向x*演化。若能到达x*这一局部渐近稳定的任务分配状态，那么在无外力干扰时，虽然无人机个体的决策行为仍然会不断更新调整，但宏观的群决策行为已经达到平衡，趋于不变。

给定李雅普诺夫函数分析x*的渐近稳定性：

(2)

沿系统式(1)的任务分配动态轨迹的李雅普诺夫函数式(2)的导数为

(3)

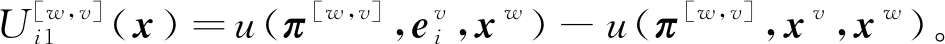
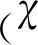
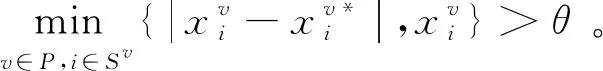
1.2 故障模型

(4)

π[wm,vk]=FvkB[w,v]+FvkD[w,v]Fwm=

π[w,v]+H[wm,vk]

(5)

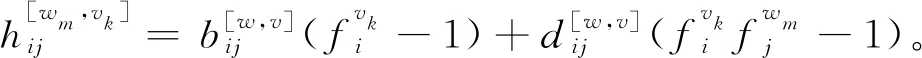
假设2保证了无人机个体在故障发生后，仍有收益未遭削弱的可执行任务存在。否则，无论向该无人机分配何种任务，蜂群的整体效益都会受到影响。

由故障模型式(4)和式(5)可知，当蜂群中部分簇内的部分无人机发生决策层面的故障时，蜂群无人机的决策能力会因此而受限。对于发生故障的无人机而言，在进行决策时，需要避免执行收益遭到削弱的任务，若选择执行此类任务，不仅蜂群的整体效益会受损，健康的无人机也可能受到故障影响，以致蜂群任务分配状态偏离期望的均衡点。

2 容错控制设计

由于故障导致某些任务的收益被削弱，所以为了保证蜂群整体效益，容错控制的目的是使无人机选择收益未被削弱的任务执行，且蜂群任务分配的状态回到期望的均衡点处。

先对蜂群无人机的自容错性能进行分析，进一步在无法自容错的情形下提出基于激励的簇间协同容错博弈控制方法。

2.1 自容错性能分析

在故障式(4)和式(5)的影响下，系统式(1)变为

(6)

(7)

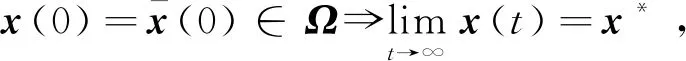
在故障式(4)和式(5)的影响下，李雅普诺夫函数的导数式(3)变为

(8)

将式(5)代入式(8)，可得

(9)

命题1如果对于系统式(6)和式(7)，满足条件：

2) ∀v∈Pf,k∈Qv+{0},xvk(0)∈intΔv。

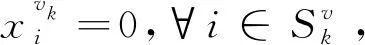
证明：

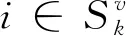
(10)

定义ξ(t,x(0))为蜂群初始状态为x(0)时t时刻蜂群的任务分配状态。式(10)沿着蜂群任务分配动态轨迹的时间导数在任何点x=ξ[t,x(0)](xvk∈intΔv)处为

(11)

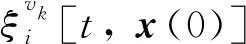
证毕

1)x*∈Ωf⊆Ω；

证明：

证毕

定理1提出了系统式(6)和式(7)自容错的充分条件，若不满足定理1所述条件，系统难以自容错。2.2节将研究在系统无法自容错的情况下，如何设计分布式簇间协同容错博弈控制方法。

2.2 协同容错博弈控制设计

倘若系统无法自容错，为消除恶意故障造成的群决策偏差行为，提出新颖的分布式簇间协同容错博弈控制方法。由于无人机个体仅通过简单的局部规则进行决策，因而发生故障后本能地倾向于最大化自身利益，这种自私和利己的特点可能会破坏任务分工这一特殊的合作形式，进而牺牲蜂群整体效益。因而邻居可以应用数据链的信息传递及机载传感器的探测，通过多源信息融合完成对故障簇的任务分配的状态感知，利用通信网络的架构针对性地向故障簇内执行不同任务的无人机传递激励信号。将该信号引入故障簇无人机的自主决策模块实现决策规则的改变，以鼓励无人机参与分工合作，从而克服无人机个体的利己性。除此以外，以故障簇为邻居的簇群也应根据故障簇的状态及所受激励，及时地向自身决策模块提供补偿信号，以免受到故障簇的影响。基本框架如图1所示。

图1 簇间协同容错博弈控制框架Fig.1 Framework of cooperative fault tolerant game control method between clusters

具体的，由于蜂群无人机的规模庞大，由其通信拓扑可得，只有发生故障的簇v∈Pf的邻居w∈Nv和以故障簇为邻居的簇l∈Lv-{v}能够获得其信息并采取相应的措施进行协同容错控制。因此蜂群无人机中各簇获取信息，处理故障的能力是有限的。

考虑故障情形∀v∈Pf，{Nv∪Lv-{v}}∩Pf=∅，并基于该情形提出分布式簇间协同容错博弈控制方法。容错控制律的设计仅在簇集Nv∪Lv，v∈Pf中进行，即仅在故障簇的邻居与以故障簇为邻居的簇集中实现容错控制。

(12)

相应地，∀v∈Pf，系统式(6)变为

(13)

(14)

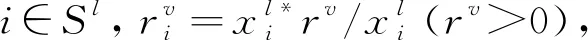
相应地，对于l∈Lv-{v}，v∈Pf，系统式(6)变为

(15)

而对于其他簇，系统式(6)不变。

考虑系统式(6)、式(7)、式(13)和式(15)在激励式(12)和补偿式(14)的作用下，李雅普诺夫函数的导数式(9)变为

(16)

式中：

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

推论1如果对于系统式(6)、式(7)、式(13)、 式(15)，满足：

1)cv>ζv，v∈Pf；

2)xvk(0)∈intΔv，v∈Pf，k∈Qv+{0}。

那么当蜂群的初始分配状态位于吸引域Ω内时，存在时间T1(x(0),cv)，簇v中收益遭削弱的任务会在时间T1(x(0),cv)内完全演化消失。

证明：

证毕

1)x*∈Ωf∩Ω；

证明：

对于v∈Pf，需要考虑以下两种情况：

情况1Lv-{v} ≠ ∅。

当t∈[T1(x(0),cv),∞)时，由条件2)和推论1可得Φf=Φc2=0。琴生不等式为

(26)

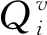
情况2Lv-{v}=∅。

故障簇v的状态并不会对蜂群内除自身外的其他簇造成影响，因而可以将该簇从蜂群中划分出来单独考虑，仅要求其本身回到原有的任务分配均衡点即可。

根据系统式(13)，给定李雅普诺夫函数分析xv*的渐近稳定性：

(27)

沿系统式(13)的任务分配动态轨迹的李雅普诺夫函数式(27)的导数为

(28)

证毕

基于定理2及其证明，在设计簇间协同容错博弈控制律，针对故障簇v构造激励矩阵(12)中的可变参数cv及补偿矩阵(14)中的可变参数rv时，需要满足指标：

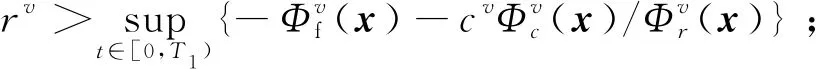
指标1)保证了蜂群无人机任务分配状态中收益受削弱的任务能够演化消失，指标2)则在簇集Nv∪Lv内实现了簇间协同容错控制。根据定理2相关证明，蜂群无人机的群决策行为仍能回到期望的均衡点处。

给出一个蜂群无人机的故障示例及相应的容错控制思路。

示例1图2是由3个簇组成的蜂群无人机，不同的形状对应于执行不同的任务。如图2所示，簇2发生一类故障，因而簇2可以看作由两个异质的子簇构成(分别用黑白两种颜色表示)：P2={20,21}。若故障可以自容错，那么无需采取任何措施；若故障无法自容错，则需构造激励矩阵C20、C21及补偿矩阵R2。

图2 一个蜂群无人机的故障示例Fig.2 An example of a UAV swarm with faults

3 仿真分析

对组织结构如图2的蜂群无人机进行数值仿真，分别对定理1、2加以验证，邻接矩阵为

(29)

簇2中发生故障的无人机占整体蜂群的比例为α21=0.1。

首先，设定2个簇的任务集合以及对应的任务收益与协作收益如下：S1={2，3}，S2={1，3}，S3={2，4}；b1=5，d11=0，d12=3，d13=1，d14=0；b2=4，d21=3，d22=0，d23=2，d24=3；b3=5，d31=1，d32=2，d33=1，d34=1；b4=3，d41=1，d42=5，d43=0，d44=4。

由系统式(1)可以得到示例1系统渐近稳定的均衡点，即原蜂群系统稳定的任务分配状态(见图3(a))为

(30)

修改3个簇的任务集合以及对应的任务收益与协作收益如下：S1={1，2，3}，S2={4，5}，S3={3，4}；b1=6，d11=4，d12=10，d13=0，d14=6，d15=5；b2=3，d21=4，d22=7，d23=12，d24=9，d25=8；b3=3，d31=6，d32=10，d33=7，d34=9，d35=8；b4=6，d43=2，d44=4，d45=6；b5=7，d53=6，d54=4，d55=0。

由系统式(1)可以得到不同初始状态下示例1系统有两个渐近稳定的均衡点(见图4(a)和图4(b))，其中期望的任务分配均衡点为

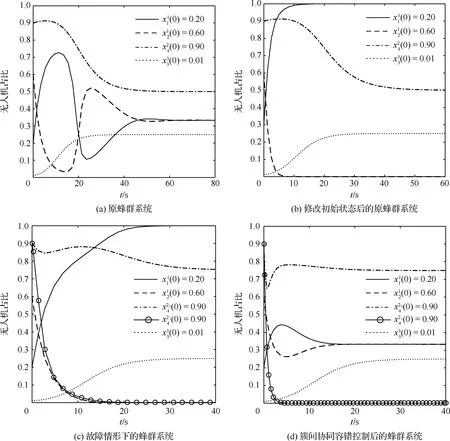
图4 任务分配动态轨迹(协同容错)Fig.4 Trajectory of task allocation dynamics (cooperatively accommodated)

(31)

由式(31)的均衡点可知，在无故障情形下，期望的稳定任务分配状态如下：簇1中执行各任务的无人机均占比1/3，簇2中执行任务4的无人机占比1/2，簇3中执行任务3的无人机占比1/4。

4 结 论

针对恶意故障下大规模分簇蜂群无人机任务分配的群决策偏差行为，建立了自容错条件，设计了簇间协同容错博弈控制方法。该方法同样适用于其他类似的蜂群系统，如机器人、智能车辆等。对于故障导致某些任务收益增加的情形，可以考虑如何利用故障的影响使得蜂群在原有的任务分配均衡点处表现更优，这是一个更为复杂且值得深入研究的问题。

未来的工作将研究在故障情况下发现和镇定其他可替代的平衡状态，这对严重破坏博弈均衡的故障具有重要的工程意义。