多飞行器的分布式优化研究现状与展望

姜霞，曾宪琳，孙健,*,陈杰,3

1. 北京理工大学 自动化学院，北京 100081 2.北京理工大学重庆创新中心，重庆 401120 3.同济大学 电子与信息工程学院，上海 200082

随着航空任务范围的不断扩大、任务复杂度的增加和网络通信能力的快速发展，航空领域需要越来越多的独立个体通信合作形成机群，来完成复杂的大规模航空任务[1-2]。比如多个无人机合作完成区域的覆盖控制和监测[3-4]、多个飞行器的编队和跟踪[5-7]、多个无人机完成对区域中事件/物体的定位[8-9]、多个体之间通信网络的拓扑优化[10]等。在大量由多个飞行器合作完成的航空任务中，飞行器之间的通信网络状态错综复杂，分布式的局部数据获取和有限的通信能力增加了航空任务完成的难度。随着航空集群规模的日益庞大，实现不同飞行个体之间合理的调度和优化任务变得尤为重要。

针对航空领域中的各种复杂的多飞行器合作决策的任务需求，大量的研究工作分别从集中式和分散式不同角度给出任务规划控制和优化设计的方案[11-12]。在不同的任务规划和优化方案中，每一个飞行器都被看作为一个具有通信和信息处理能力的自治节点。在集中式方法中，存在一个集中的节点，从各个子节点收集局部检测的数据，在集中节点进行优化决策，然后再传输给子节点进行控制决策。每个节点都需要与集中节点进行大量数据的双向通信，通信负担较大，并且集中式的方法对中心计算节点的算力要求很高。在分散式优化方法中，部分数据在子节点进行局部处理时，仍然需要中心节点进行融合处理并将结果反馈给子节点。由于航空任务中飞行个体物理隔离，任务数据分布在不同的个体上，并且个体之间的通信网络由于通信带宽和稳定性等原因变得复杂多变，因此，集中式和分散式的优化控制策略往往无法高效、鲁棒地完成复杂的航空任务。

在由多个个体组成的网络系统中，物理隔离的个体由于具有独立的收集、处理和传输数据的能力，可以通过通信网络以合作的方式，在本地利用局部和邻居信息进行总体优化问题的求解，称为分布式优化[13]。近些年迅速发展的无人机集群作战就是分布式优化应用的重要场景之一，例如对动态敌对环境或危险环境的信息搜集，包括野火监测、搜索救援任务、侦察监视任务等，多个飞行器的分布式协同优化可以避开空间内的障碍限制，最大限度地探测任务空间内的事件，完成监测事件有效的数据收集。飞行器在空中作战或者网络状态不佳的领域中，通过机载的通信传感器搭建通信网络。通过对不同飞行器之间通信拓扑状态的分布式优化，增强飞行器之间通信的鲁棒性，对环境干扰和敌方进攻都有很好的抵御作用。与集中式和分散式优化相比，分布式优化方法具有很多优点。在分布式优化中，每个飞行器将局部感知信息存储在本地，并在本地节点进行迭代处理，由于本地数据规模较小，飞行器节点的计算和存储负担降低。每个飞行器通过和网络拓扑中的邻居飞行器节点进行通信完成总体任务的优化，无需中心节点的存在，不依赖于中心节点的处理，由此避免了与中心节点的双向通信，可以及时对局部任务变化做出反应，灵活性更高。分布式优化具有更好的可扩展性和鲁棒性，可以有效实现数据的隐私保护，在航空应用中有很重要的意义。基于以上优点，分布式优化在航空领域得到了广泛的关注和应用。

经过近十年的发展，多飞行器的分布式优化问题的研究无论是从理论层面还是在实际应用中都取得了长足的发展，本文从分布式优化的研究现状、研究的热点难点以及未来的研究发展方向这3方面对分布式优化的理论研究工作进行简要的归类介绍。由于近些年来国内外的分布式优化成果较多，虽不能求述其全貌，但尽可能地包含近些年来应用最广泛的成果和工作。

1 分布式优化的研究现状

1.1 问题模型

在分布式优化问题中，每个个体仅知道自己的局部目标函数和约束信息，且这些信息由于隐私、安全等原因无法通信，导致分布式优化算法的设计和分析变得复杂。在由m个个体构成的网络系统中，个体之间通过通信网络，分享局部优化决策变量来共同最小化(最大化)一个全局目标函数，称为分布式优化问题。本文主要讨论基于个体间共识的分布式优化问题，其全局目标函数往往是个体局部目标函数的和函数：

式中：x∈Rn是全局优化决策变量。由于局部目标函数信息fi分布在不同的个体上，因此需要在每个个体上对全局优化变量x进行局部估计，即局部估计变量xi。分布式优化问题的信息分布如图1所示，不同个体i∈{1,2,…,5}之间通过网络通信局部决策变量。

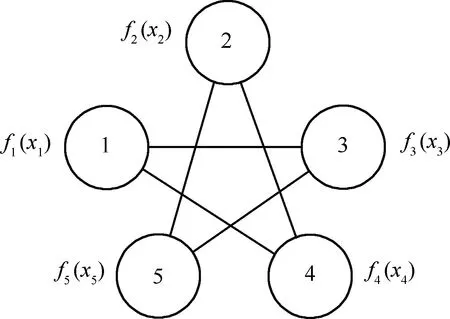
图1 分布式优化问题模型Fig.1 Model of distributed optimization problem

对于分布式一致共识优化问题，既需要达到全局目标的最小化(最大化)，又需要保证网络中不同个体i、j的局部估计优化变量达到一致，即xi=xj。对于分布式资源分配等非基于个体间共识的分布式优化问题，由于篇幅原因，本文暂不做讨论，相关介绍可以参考文献[14-16]。

分布式优化问题的优化模型包含四大要素：变量、代价函数、约束和通信网络。

1) 变量：在分布式优化中，不同个体之间由于隐私安全或者带宽限制等原因，无法共享局部函数信息和约束信息，只通信局部优化变量，对于带约束问题，根据算法设计的需要，共享对偶变量和辅助变量。因此，分布式算法可以有效地保护局部信息的隐私。

2) 代价函数：对于不同的应用场景，分布式优化会有不同类型的代价函数，不同的代价函数有其特定的性质，影响分布式优化算法的收敛性能和适用范围。按照代价函数是否光滑，可分为光滑函数、非光滑函数。按照函数的凹凸性分为凸函数、严格凸函数、强凸函数和非凸函数。按照函数信息是否随时间实时变化分为时变函数和时不变函数。一个分布式优化问题的代价函数可以由不同类型的函数构成，比如在经典线性回归问题中，目标函数由光滑凸函数和非光滑L1正则函数构成。

3) 约束：实践应用中的分布式优化问题，往往存在一些现实的约束。按照约束的类型，可以分为集合约束、等式约束和不等式约束。根据不同的实际应用，集合约束既可以是全局的集合约束，也可以是多个局部集合约束的交集；等式约束可以是线性的或非线性的；不等式约束可以是凸的，也可以是非凸的。

4) 通信网络：分布式优化基于传输网络进行个体间信息的交互。根据实践中网络拓扑结构是否时变分为固定拓扑和动态拓扑。根据信息传递是否具有方向性分为无向图和有向图。根据网络拓扑的连接结构可分为平衡图和非平衡图。在实际应用中，网络通信往往会出现拥堵，造成通信延迟，因此很多工作研究存在时间延迟的通信网络下的分布式优化[17-20]。

1.2 分布式优化方法研究框架

本节将从不同角度对现有的分布式优化方法的研究框架进行分类介绍。

1.2.1 按原始变量和原始-对偶框架的算法分类

一般的分布式优化问题形式为

(1)

式中：函数g是约束函数，对于分布式优化问题，约束函数往往包括不同个体之间局部变量一致的等式约束；变量x是优化问题的原始变量。该优化问题的拉格朗日对偶函数为

对偶问题为

maximizeyr(y)

subject toy≥0

其中：变量y是优化问题的对偶变量。函数

L(x,y)=f(x)+yTg(x)

称为原始优化问题的拉格朗日函数。对于不等式约束的凸优化问题，在一定假设下，原始问题的最优变量x*和最优对偶变量y*满足如下Karush-Kuhn-Tucker (KKT)条件，即

相关的理论证明可以参考文献[21]。

直接对原始优化问题进行求解的方法称为基于原始变量的优化方法，例如对于一般无约束优化问题，梯度法、牛顿法及其变种方法[21]都是原始变量法。对于带有一致性约束的分布式优化问题，可以通过变量一致技术[22-23]或者梯度跟踪技术[24-27]实现对原始优化问题的高效求解，具体的算法设计在1.3节中讨论。对于带有不等式约束的优化问题，经常用的算法之一是利用惩罚项将约束引入目标函数，利用外罚函数法或者内点法[28]进行求解。这些方法都是原始变量法，直接对原始变量进行迭代更新。

处理带约束分布优化问题的另外一种思路是通过引进对偶变量，构造最优解的KKT条件，利用KKT条件构造优化算法。一些典型的原始-对偶法包括对偶分解法[29-30]、增广拉格朗日乘子法[10]、原始-对偶法[31-33]、交换乘子算法(ADMM)[34-36]等。原始-对偶方法对比原始变量法，在进行分布式优化问题的算法设计时，设计代价较低，分析方法较为普适。但是对比原始变量法，其增加了优化算法的维度，加大了存储空间代价。

1.2.2 按梯度阶数的算法分类

根据分布式优化算法设计中使用的函数梯度信息分为一阶梯度法、二阶梯度法和零阶梯度法。在算法迭代时，如果需要利用目标函数的一阶梯度信息，则该类算法称为一阶算法；如果变量迭代时需要利用函数的二阶导数信息或者Hessian矩阵信息时，则该类算法称为二阶算法；如果算法迭代时，没有利用到函数的任何梯度信息，则称为零阶算法。

一阶算法[26,37-39]是处理分布式优化问题最为常用的方法，因为其一阶梯度的计算代价较低，易于写成分布式的结构，且一阶算法的收敛性分析较为成熟，满足大多数应用对于收敛精度的要求。二阶算法[40-42]在求解低维优化问题时，往往比一阶算法具有更快的收敛速度，但是函数的Hessian信息往往求解代价较大，无法应用于高维复杂的优化问题，因此很多工作[40,42]也在探究估计二阶信息的方法，来弥补其求解代价大的不足。在一些实际应用中，比如函数信息为噪声函数值时，或者函数为区间函数时，精确的梯度信息往往求解困难，算法往往根据函数值来对梯度进行估计。零阶梯度法[43-45]利用近似梯度的思想，通过函数值对梯度信息进行近似，实现只利用函数信息对问题进行优化。

1.2.3 按连续时间和离散时间的算法分类

根据变量迭代方式的不同，分为连续时间算法和离散时间算法。在节点位置配置、网络拓扑优化、资源能量分配等应用场景中，适用离散时间算法[37-50]。而且离散时间算法可以利用高性能的计算机进行快速迭代求解。但是在一些变量状态连续变化的系统任务应用[51]中，例如多运动体的最优编队、最优位置姿态控制等，离散算法无法保持变量值的连续。可以通过搭建模拟电路实现低成本、低功耗的连续时间求解器来求解问题。因此，近年来连续时间算法[52-54]受到了研究者的关注。

连续时间算法和离散时间算法除了在任务应用和算法实现方面不同外，在算法的分析方面，也有较大的差异。离散时间算法的分析往往利用差分方程的分析思路讨论优化变量距离最优解的距离变化，或者是函数值随着迭代次数增加的收敛变化。而连续时间算法的分析往往是通过提出合理的李雅普诺夫函数，通过利用稳定性理论来讨论优化变量和函数值的收敛变化。

1.3 典型的分布式优化算法

针对分布式优化问题的不同模型要素和研究框架，研究者提出了多种分布式优化算法。由于工作较多，本文只简要介绍无约束分布式凸优化问题、集合约束的分布式凸优化问题、不等式约束的分布式凸优化问题和分布式非凸优化问题的典型分布式一阶算法研究成果。关于分布式二阶算法和零阶算法的研究，可以参考文献[40-41，52]。在不加说明的情况下，本文的通信拓扑都指代无向图，除非另有说明为有向图。

1.3.1 无约束分布式优化

针对模型目标问题为凸光滑函数的无约束优化问题，其典型的应用之一是多个体一致性问题。例如，文献[55]提出的多个无人机的分布式优化部署问题，需要在每架无人机上进行本地运算，单独决定其运动的控制框架就是一个典型的无约束优化问题。

利用变量一致性技术，分布式梯度下降、分布式增量梯度下降法等都可以实现对优化问题的高效分布式求解。无约束分布式优化问题和算法设计架构如下：

其等式约束是为了保证局部估计变量达到一致，局部变量估计xi∈Rn。对于分布式优化问题，局部代价函数最优并不等价于全局代价函数最优，因此，需要在保证局部估计变量一致的约束下，优化总体代价函数。基于变量一致性技术的经典分布式梯度下降(DGD)算法设计为

(2)

式中：aij为拓扑图邻接矩阵的第i行第j列个元素，步长αi为衰减步长，可以保证算法的有效收敛。同时，为了加快收敛速度，很多优秀的工作通过使用历史信息，设计固定步长的分布式算法，典型的工作包括EXTRA[37]、PG-extra[46]以及EXTRA的推广方法[47]。考虑到个体更新梯度可能存在随机误差，文献[23]提出在动态连通拓扑下的分布式随机增量梯度法，使得不同个体的局部变量均收敛到共同的全局最优解。

另外一种设计分布式优化算法的思路是利用梯度跟踪技术，根据不同梯度跟踪方法，提出不同的分布式优化策略DIGing(Distributed Inexact Gradient Tracking Method)[24]、Aug-DGM(Augmented Distributed Gradient Method)[25]、AsynDGM(Asynchronous Distributed Gradient Method)[26]和ATC-DIGing(Adapt-Then-Combine ariation of DIGing)[27]。经典的方法之一如下该算法运用固定迭代步长，可以实现静态图下不同个体变量收敛到共同的全局最优解。进一步的，DIGing算法和Push-DIGing算法[24]分别实现了动态拓扑图和有向图下的有效收敛。尤其，在优化问题的代价函数为强凸时，梯度跟踪方法可以达到比变量一致方法更好的指数收敛性能。图2对以上所提算法之间的关系进行了汇总比较，以上方法均为在原始域内进行优化的分布式算法。

图2 分布式算法关系图Fig.2 Relationships of distributed algorithms

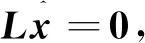
如果拓扑图为无向图，则L=LT，其对应的原始-对偶变量迭代公式为

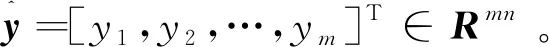
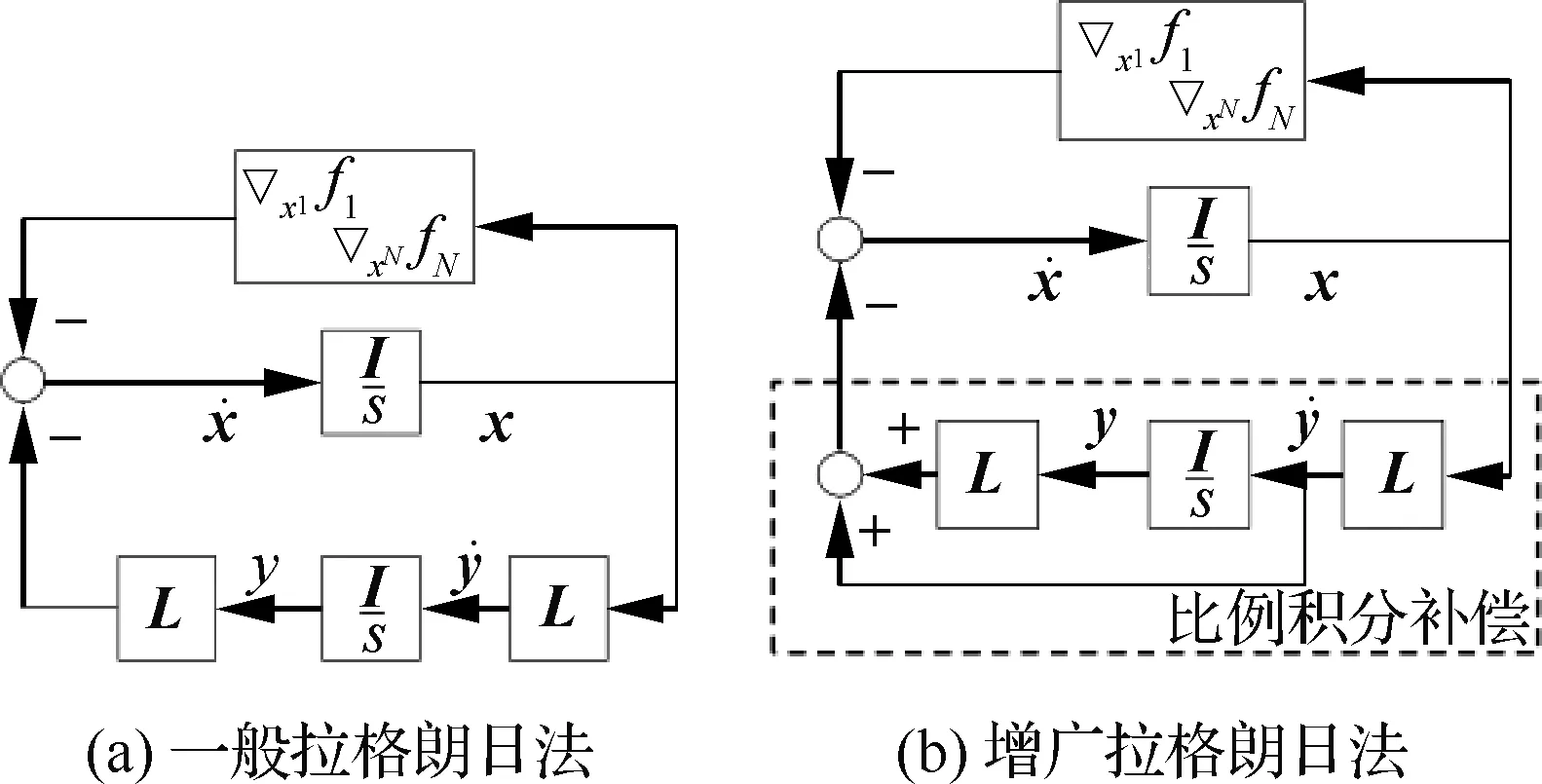
图3 增广拉格朗日法对应比例积分反馈控制Fig.3 PI control viewpoint for augmented Lagrangian method

基于原始-对偶设计框架，提出不同的分布式优化求解方法，包括原始-对偶方法[31,60-61]、对偶分解法[30,62]、交替方向乘子法(ADMM)[34-36]、交替最小化[42,63]等。在对无人机编队问题中的协作问题，文献[64]提出基于对偶分解技术的算法，直观地用许多较小的可处理问题代替了一个大型的计算难题，返回原问题的一个可行解。类似的，在ADMM法、交替最小化方法中，原始变量不采用原始方法中的梯度下降迭代方法，而是采用当前子优化问题的最优值。具体来说，对于多变量的无约束分布式优化问题，通过引入连通拓扑图的边点关联矩阵A∈Rmn，可以得到如下的优化问题

式中:α为与时间无关的固定更新步长，其取值往往与目标函数的参数有关。

虽然每次迭代都要求解一个子优化问题，但是当子问题可以获得封闭解或者易于求解时，交替乘子算法往往具有更好的实际应用性能。上述多变量算法实际上是针对双变量分布式优化问题的ADMM推广，可以更为高效的求解多体分布式优化问题[65]。进一步的，文献[66]给出了无次序更新的交换乘子分布式求解方法，减少了对于通信拓扑和更新顺序的依赖，扩大了算法的应用范围。

1.3.2 集合约束的分布式优化

对于凸集合约束下的优化问题，在文献[67]中，针对个体在障碍存在的环境下的路径规划问题，讨论了如何建立问题的优化模型，并设计算法有效求解多障碍集合约束下的优化问题。在任务问题中，当个体存在凸集合约束时，其分布式优化问题模型为

式中：Ωi为个体i的局部凸集合约束，这样的分布优化问题又称凸交问题。在多个飞行器任务中，由于单个飞行器的计算、通信和可见半径有限，需与其邻居共享信息以进行协调，因此，在有动态或者静态障碍物环境下的多个体编队与导航就是一个典型的分布式凸交问题[68]。

当优化问题的集合约束为局部约束的交集时，文献[13]提出固定/时变连通图下的高效分布式投影算法为

式中：PΩi(·)为向局部可行集合Ωi投影操作。当梯度为零时，该算法退化为求解一致性优化问题的分布式算法，对应的算法投影示意图如图4所示，其中对于i∈{1,2}，

图4 分布式投影算法图示Fig.4 Illustration of distributed projection algorithm

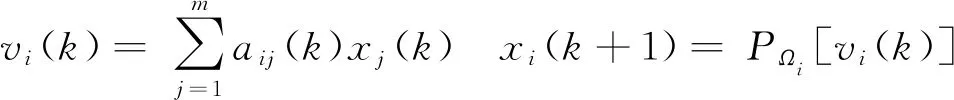
式中:aij(k)为k时刻的多节点网络拓扑的邻接矩阵元素。

文献[69]进一步将该算法拓展到时变有向平衡图，并考虑了在存在各种不确定性的情况下，包括有噪声的通信链路、随机通信图以及目标函数次梯度评价中的随机误差时的分布式优化问题。由于优化问题信息的分散化和集合投影运算代价较高，文献[70]中提出不精确的凸投影共识算法，降低了投影运算的代价，使不同个体达到全局凸交集中共同的最优解。

1.3.3 不等式约束的分布式优化

在一些多飞行器的应用任务中，任务的个体既需要满足自身的集合约束，又需要满足不等式函数或者等式函数约束。由于等式约束可以用不等式约束表达，仅讨论不等式约束的分布式优化问题。包含多种集合和不等式约束的分布式优化问题形式如下

式中：函数f(x)、g(x)为凸函数，全局不等式约束认为是分量满足的，也就是说分量gl(x)≤0，l∈{1,2,…,m}。不同个体的约束函数gl(x)既可以是统一约束函数，也可以不同。一般的优化方法是通过引入对偶变量，根据优化问题的KKT条件，设计对应的求解算法。例如，在文献[64]中利用原始-对偶的思想，对由大量的无人机组成的网络，在分布式、易受干扰、可能存在竞争的环境下，研究了一个新的分布式控制框架，实现完全可重构的无人机网络平台。针对优化问题，其对应的拉格朗日函数为

L(k)=f(x(k))+mμTg(x(k))=

式中，μ∈Rm为不等式约束对应的对偶变量；Li(k)为个体i对应的拉格朗日函数。基于拉格朗日函数鞍点的性质，文献[71]提出了分布式拉格朗日原始-对偶次梯度算法为

式中:Mi为对偶域，收敛步长α(k)为衰减步长。该算法实现了在切换有向拓扑连通下，渐近稳定收敛到全局最优点。然而，衰减步长算法随着迭代次数的增加，收敛速度将受到限制。在固定连通拓扑下，文献[32]提出了具有非一致固定步长的分布式优化方法，并且在每个协商一致步骤中执行多个协商一致更新的情况，加快了个体的收敛性能。文献[33]研究了时变拓扑网络中带约束凸优化问题的最小化问题，通过设计正规化的拉格朗日函数，提出了一种基于一致性的正则化原始-对偶次梯度法。该方法的实现只需要在最后一次迭代时进行一次投影，避免了每次迭代都需要进行投影运算的代价。

1.3.4 分布式非凸优化

在现实应用中，由于很多任务目标或者约束都是非凸的，非凸优化的算法成为近些年来研究热点和难点。航空任务中，比如路径规划、最优覆盖等任务中存在很多非凸问题。解决方法之一是将非凸优化问题转化为凸优化问题，利用凸函数的性质进行求解。例如，针对基于非凸二次型的飞机三维路径规划问题，文献[72]将非凸规划问题转换为半正定优化问题，利用半正定优化得到其最优值的紧下界，然后再利用秩最小化得到规划问题的最优函数值。

非凸问题的另一种解决方法是直接针对非凸优化问题，通过one-point凸技术或者近似技术提出有效的求解方法。针对具有特殊结构的非凸优化问题，文献[73]提出了分布式梯度下降法，并证明了在一定条件下，算法收敛到非凸优化问题的二阶驻点(Second-Order Stationary Point)。分布式随机梯度下降是目前直接处理非凸优化问题的比较成熟的方法，可以有效逃离严格鞍点，具有较好的收敛性能，一些典型的分布式随机梯度优化算法工作包括文献[74-78]，其经典的算法设计如下：

αkgi(xi(k))

式中:αk、βk为可调节步长；aij为通信网络邻接矩阵元素；gi函数为局部函数梯度估计，该梯度既可以是简单随机梯度，也可以是小批量随机梯度或随机拟牛顿方向。上述算法是基于变量一致原则进行分布式算法设计。针对经验风险最小化问题，即

文献[79]中基于梯度跟踪技术，给出如下分布式随机梯度算法设计：

对于目标函数中含有不可微子函数的双变量非凸优化问题[80]，优化的思路是使用交替最小化的方法来解决，并进一步推广到多变量的情景。包含不可微的非凸优化问题的一般形式为

minimizex,y∈Rnf(x,y)=J(x)+F(x,y)+R(y)

(4)

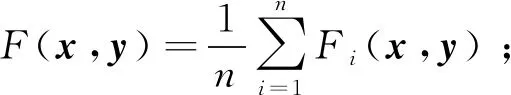
式中:γx、γy分别为可调节的更新步长。由于该算法的子问题往往无法得到封闭解，需要内部子迭代，降低了算法的性能。针对这个缺点，文献[81]中利用近似算子，提出线性化算法(5)，使得子问题可以进行高效求解，提高了交换乘子法的性能,

(5)

其中，近似算子定义如下

算法(5)可以保证收敛到非凸问题的驻点，目前已有一些优秀的工作探讨了方法求解非凸优化问题的收敛性能，并提出了该方法的加速和随机版本[82-83]。方法(5)可以由处理双变量问题扩展到处理多个变量的问题，但是每个变量更新都需要完整的F函数的信息，不适用完全分布式的优化问题。针对个体之间拓扑连通的情况，文献[38]中，提出了完全分布式的近似梯度法(Prox-DGD)，保证了无向连通网络中每个个体的局部变量都收敛到非凸问题的驻点。

针对不同类型优化问题，本文提及的相关算法工作可以粗略汇总如表1所示。从表1数据可以看出分布式凸优化成果丰富，而分布式非凸优化的理论研究较少，尤其是集合约束下和不等式约束下的非凸优化问题，这也是分布式优化研究的难点方向之一。

表1 分布式算法工作汇总Table 1 Summary of distributed algorithm works

2 分布式优化的研究难点和未来展望

2.1 分布式优化的研究展望

由于数据规模的迅速增大和信息的分散化，分布式优化的研究近些年来得到了广泛的关注和长足的发展。未来分布式优化的研究展望包括如何加速分布式优化算法，在动态网络连接状态下分布式优化算法设计以及对于复杂的带约束非凸优化问题，如何设计分布式优化算法。

2.1.1 分布式加速算法

实现分布式优化算法加速的另一个方法是利用方差减小(Variance Reduction)的技术。对于数据样本量很大的优化问题，求取完整的个体梯度仍然是一个耗时的操作，在对实时性要求较高的实际航空任务中，难以实现求取完整的个体梯度，因此很多研究工作中，采用随机采样个体本地的样本数据求取个体的随机梯度的方法来估计完整梯度。方差减小技术可以降低局部的梯度方差，使得个体可以用随机采样的个体梯度来估计完整的个体梯度。文献[84，92，93]将不同的方差减少技术与基于变量一致的分布式算法结合，提出了更为高效的分布式优化算法，降低了计算完整个体梯度的代价，使得算法在面对实际任务中大规模数据时仍然可以高效地决策控制，但是同时利用梯度跟踪和方差减小技术实现局部和全局梯度的准确估计，从而降低步长对于大规模数据样本问题下优化算法的影响，进一步提高分布式算法的性能，目前还未有较为成熟的理论研究。

2.1.2 动态拓扑下的分布式优化

针对大规模多个体网络上的分布式优化问题，分布式算法的性能受到个体之间网络拓扑连接的影响。受航空任务环境中各种复杂因素的影响以及网络通信带宽的限制，个体之间的有向/无向拓扑连接往往是动态变化的。文献[22]中，讨论了在无向动态拓扑下的分布式优化问题，并给出了基于变量一致的分布式梯度下降方法的收敛性能。对于基于梯度跟踪技术的分布式优化方法，文献[24]中给出了其可以实现在动态拓扑上达到线性收敛速率的分析。由于网络资源有限，在航空任务应用中，无向网络拓扑往往难以实现，飞行器之间大多以有向通信拓扑连接为主。针对动态有向拓扑下的分布式凸/非凸优化问题，文献[95-97]提出了高效的分布式优化算法，并给出了收敛性能分析。对于动态有向/无向连接拓扑，文献[98]使用通信轮数和梯度评估之间的优化比率，实现算法快速收敛，并且，根据梯度评估的数量来衡量，该算法迭代收敛到全局最优解的速度与集中式梯度下降相同。

2.1.3 带约束的非凸优化

在多飞行器完成的航空任务中，比如路径规划、最优覆盖等，很多任务目标或者约束都是非凸的，文献[72]已经研究了在无约束情况下非凸二次型的飞机三维路径规划问题，当非凸问题中包含集合或者不等式约束时，算法的设计需要进一步改进。对于带有全局集合约束的分布式非凸优化问题，文献[99]基于梯度跟踪的思路，提出了分布式非凸优化方法，证明了个体局部变量达到一致的变量均值，并收敛到优化问题的共同驻点。对于带有线性等式函数约束的非凸优化问题，文献[80]从原始-对偶的角度给出了高效的分布式优化算法，并证明了算法可以以次线性收敛速度，全局收敛于驻点集合。当非凸优化问题具有更为复杂的非线性耦合的非凸约束时，文献[29]从对偶角度，提出了双层迭代的优化方法，并给出了可以收敛到优化问题KKT解的严格证明。但是，目前对于各种约束下的非凸优化问题的研究，都未给出收敛到全局最优解的性能分析。对于现实航空任务中更为复杂约束下的非凸优化问题，其高效的分布式算法设计仍然是目前的研究热点。

2.2 分布式优化的共性难点

在大规模多飞行器的分布式优化中，个体之间借助机载通信设备网络实现信息的交互。不同飞行器之间的计算时序和速度有差别，通信能力有限，且环境干扰因素较多，因此本节中对通信时延、干扰误差、异步迭代和通信计算权衡等是分布式优化算法设计中共有的难点进行简要介绍。

1) 通信时延是大型网络中不可避免的通信问题。当个体在与邻居之间的通信延迟时间一致并可能无限大时，文献[17]给出了分布式算法求解可微凸目标函数的收敛速度与网络大小、拓扑结构和处理器间通信延迟的函数关系的上界。基于无源性理论，文献[18]分析了在无向固定拓扑下，连续时间算法求解分布式无约束和有约束优化问题时，如何有效处理任意未知的恒定通信延迟。对于梯度连续的强凸代价函数，文献[19]研究了在具有时变延时的有向图下，分布式算法保证所有的个体收敛于系统最优解的充分条件。但是针对实际应用中更为一般的优化问题，如何在复杂的网络通信情况下保证分布式算法的收敛性能仍然是目前的难点问题。

2) 个体迭代利用的梯度信息无法精确获得。单个个体在利用梯度信息进行迭代时，由于外界环境的干扰或者自身运算误差等原因，往往无法得到精确的梯度信息。在动态切换拓扑连通图下，文献[23]针对全局集合约束的分布式凸优化问题，提出了分布随机次梯度投影算法，探讨了随机次梯度误差对算法收敛性能的影响，保证算法的有效收敛。文献[19]进一步将工作扩展到非凸优化问题，证明了通过合理调整步长，分布式随机梯度方法仍然可以收敛到问题的临界点集合。但是对于非凸优化问题，并未给出全局收敛的理论研究结果，随机梯度误差对任务中复杂有向拓扑下分布式算法的收敛性能的影响目前还没有研究成果。

3) 同步的全局时钟在分布式算法应用中难以满足。在分布式系统中，同步的分布式算法需要全局时钟进行时序控制，因此往往无法适用于实际的应用场景。在无法保证同步的全局时序情况下，大量的工作研究分布式异步算法，以确保个体在本地时钟下局部迭代仍然可以实现全局收敛，而无需时钟同步。异步的分布式优化方法同时也解决了由信息时延带来的无法获得实时信息的问题。异步优化方法可以分为完全异步方法和部分异步方法，相关的工作可以参考文献[100-103]。完全异步方法由于假设严格，只有少数算法可以在满足假设的情况下，实现高效异步收敛；而对于部分异步方法，目前的分布式算法研究主要集中在收敛性上，而对于算法的收敛速度以及动态有向拓扑网络下的分布式算法研究成果较少。

4) 合理地平衡分布式算法的计算负担和通信负担是影响算法性能的重要因素。在多个体网络中，由于不同个体在物理环境中分离，个体之间的通信带宽有限且不稳定，迫切需要减轻网络的通信负担。研究分布式优化算法的通信效率问题，尤其是在经验风险最小化方面，近年来得到蓬勃发展。文献[104]系统地探讨了分布式算法的收敛速度与节点通信的网络的结构和性质之间的关系，介绍了目前先进的分布式算法在不同的网络拓扑场景下的性能分析。文献[105]针对协调控制方案中全局决策变量的快速分布式计算任务，分析了重复通信与计算之间的权衡问题。文献[39]强调了网络拓扑结构、跨个体的数据同质性以及全球通信和本地计算之间的精确权衡影响。但对于在实际应用中，如何在动态通信网络状态下，合理平衡计算和通信仍是目前研究的难点。

3 总结与展望

本文聚焦于航空领域现有和未来可能出现的分布式优化的问题，从研究框架、主要研究成果、研究难点和未来展望3个方面出发，对近些年来分布式优化的研究工作进行了简要介绍。根据优化问题的差异，对无约束的分布式凸优化、集合约束的分布式凸优化、不等式约束的分布式凸优化和分布式非凸优化目前的典型研究工作进行了概述。其中，一些无约束和有约束的分布式凸优化问题，已经有很多成熟的算法工作，形成了解决方案，应用在商业软件中，用来解决国民生产、军事国防中遇到的各种分配和优化问题。针对由多个个体组成的大规模网络系统，分布式优化工作仍是一个研究热点。

目前的分布式优化工作在航空任务应用中仍然存在很多不足。① 多机体之间的通信速度和带宽的限制在分布式算法设计时没有充分考虑。② 在执行任务时存在大量信号干扰，导致算法迭代存在误差，无法精确执行。③ 在实际应用中，难以保证不同机体间时钟同步，高效的异步分布式算法研究不足。④ 单个机体的通信能力和计算能力很有限，而且隐私数据无法进行传输分享，这对如何在实际应用中合理平衡计算与通信提出挑战。这些也是分布式优化算法理论研究的热点，如果能将目前理论研究的成果与航空领域中出现的优化问题有效结合，可以为多机体的航空任务提供更有效的解决方案。