航天器自主导航状态估计方法研究综述

王大轶，侯博文,*，王炯琦，葛东明，李茂登，徐超，周海银

1. 北京空间飞行器总体设计部，北京 100094 2. 国防科技大学，文理学院，长沙 410073 3. 北京控制工程研究所，北京，100094

航天器的导航、制导与控制[1-2]大多需要依靠地面设备来完成，主要方式是采用地面站光学和无线电系统对航天器进行跟踪测量，然后再由计算机确定航天器的位置，经上行遥控设备将运动参数和控制指令注入到航天器上，再由其在轨实施。随着航天器在深空探测、国防应用、导航通讯等多个领域发挥着越来越重要的作用，人们对航天器在轨自主运行的要求也越来越高。

航天器自主运行主要涉及自主导航、自主制导与控制、自主任务规划、自主诊断重构等多个方面，其中自主导航是核心技术之一，是航天器实现轨道/姿态自主控制、执行深空探测、在轨服务等空间任务的前提[2-3]。截至目前，国际上有影响力的航天大国已经在航天器自主导航技术上取得了众多研究成果，并进行了多次飞行试验[4-6]。

航天器自主导航[1-2]指的是在不依赖地面支持的情况下，仅利用自身携带的测量设备在轨实时确定航天器位置、速度、姿态及其他导航参数的技术。状态估计是实现航天器自主导航的核心手段，利用自身携带设备获得测量数据，结合航天器导航系统状态的动力学/运动学模型，对带有误差的观测数据分析处理，通过递推计算实时地获得航天器的位置、速度和姿态的过程。传统的状态估计方法主要包括最小二乘法、批最小二乘法、迭代最小二乘法和卡尔曼滤波算法(Kalman Filter, KF)等。KF算法最早应用于“阿波罗”计划轨道预测，后来逐渐在航天器自主导航状态估计中发挥着越来越重要的作用[7]。

航天器在轨状态估计精度是影响自主导航系统性能的主要因素[8-9]。为了提高自主导航性能，早期的大多状态估计方法主要通过改进滤波算法来提高状态估计精度。改进的方式主要有基于系统模型近似的滤波方法和面向系统误差抑制的鲁棒滤波方法。这些算法在自主导航领域都有较为广泛的应用，但是随着任务需求的变化，自主导航系统模型越来越复杂，在轨运行环境不确定性因素越来越多，受星上资源和计算能力的约束，现有的模型近似算法的精度有限，鲁棒滤波算法的计算复杂度高，难以实现导航系统星上自主的高精度状态估计。

针对上述问题，近20年来，航天器自主导航状态估计方法研究取得了突破性的进展，主要是将系统性能分析、误差在轨估计与补偿等引入到状态估计研究中。许多研究机构和学者通过自主导航系统的可观测性评价来分析导航系统状态估计精度，并将系统误差作为待估参数纳入到导航系统的状态估计研究中，为航天器自主导航系统高精度状态估计提供了新的方向。

综上所述，本文针对航天器自主导航状态估计方法的研究意义、研究现状及应用现状进行了系统、全面的梳理、归纳与总结，具体结构安排如下：① 结合航天器自主导航的任务需求，介绍了状态估计的研究意义；② 对状态估计的研究现状进行了详细梳理，包括可观测性分析、导航滤波算法设计及系统误差在轨补偿；③ 系统地归纳了状态估计在航天器自主导航领域的应用情况；④ 提出当前研究存在的主要问题并对其后续发展进行展望，为我国未来航天器自主导航任务提供参考。

1 航天器自主导航状态估计方法研究现状

目前，航天器自主导航状态估计方法已经有了很多研究成果，需要进一步明确其研究现状，才能更加有针对性地对其开展深入研究。本节结合航天器自主导航系统特点，对状态估计方法的研究现状进行介绍。

航天器自主导航状态估计方法的研究内容主要包括：可观测性分析、导航滤波算法以及系统误差补偿。具体研究内容如图1所示，下面将结合图1对自主导航状态估计方法的研究现状进行归纳总结。

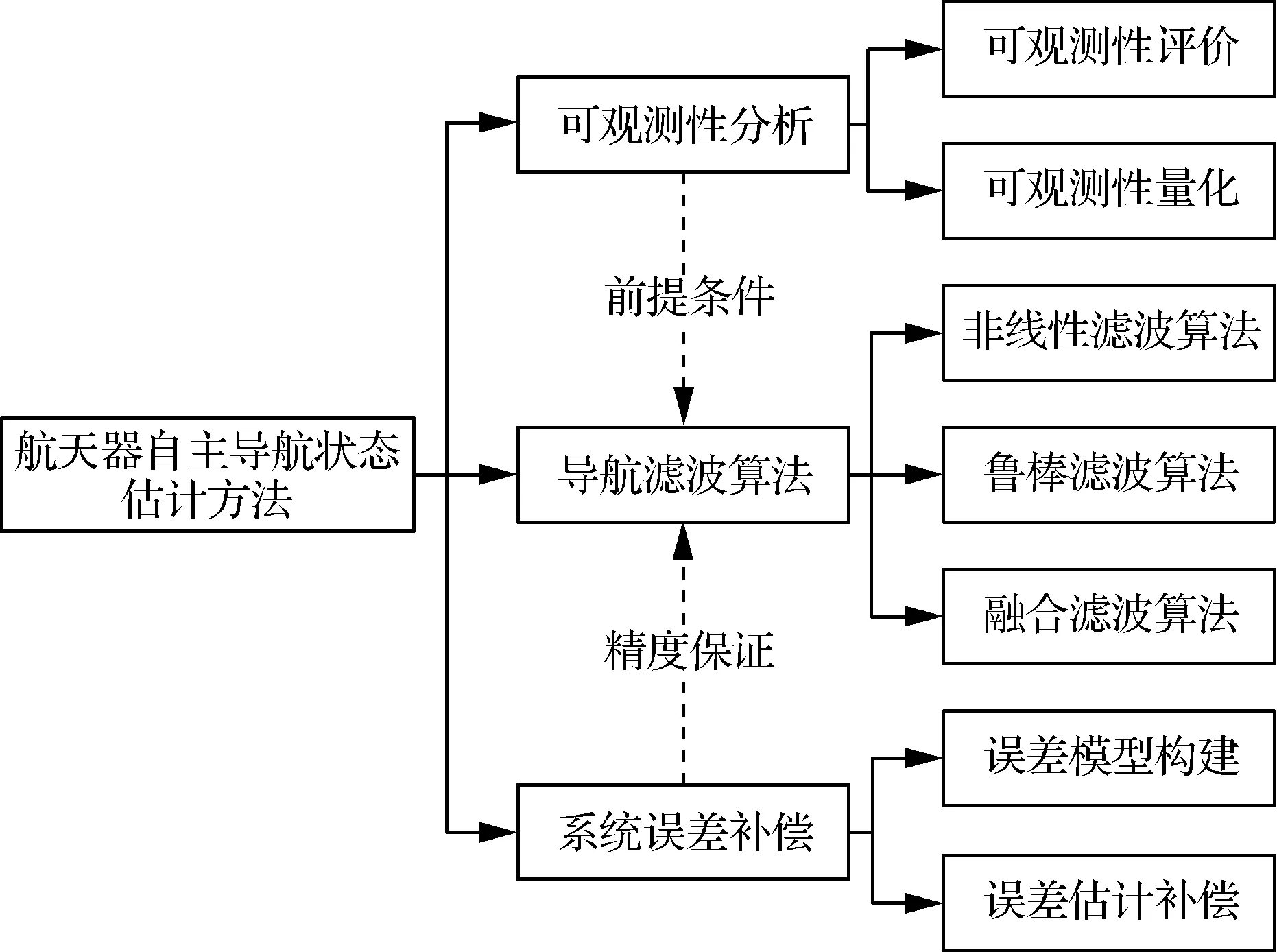
图1 航天器自主导航状态估计方法研究框架Fig.1 Research framework of autonomous navigation state estimation method for spacecraft

1.1 可观测性分析研究现状

可观测性最早是由美国科学家卡尔曼提出来的[10-12]，反映了系统根据有限时间内观测量确定系统状态的能力[13]。系统满足可观测性条件是通过导航滤波算法实现系统状态估计的前提。

可观测性分析可以细分为性能判定和定量描述2个子问题，前者主要分析其性质的有无，是一个非此即彼的判定问题；后者是分析性能的大小，是一个性能量化评价的问题。因此，航天器自主导航系统的可观测分析问题主要归纳为：系统可观测能力定性分析方法和系统可观测能力量化方法。下面分别对这两类问题的研究现状进行介绍。

1.1.1 系统可观测能力定性分析方法

很多学者通过分析导航系统可观测性来判断其是否具备实现状态估计的能力，并以此作为航天器自主导航系统设计的合理性。按照导航系统的性质，系统可观测性分析方法主要分为线性系统可观测性分析方法和非线性系统可观测性分析方法。

1) 线性系统

针对线性系统的可观测性分析问题，最早是由Müller和Weber[14]在1972年提出的系统可观测性的度量问题。他首先系统地研究了线性系统的可控性格拉姆矩阵，并将其应用于系统可观测性分析。

随着导航技术的发展，格拉姆矩阵开始逐渐应用于导航系统可观测性分析[15-16]。但是航天器自主导航系统大多为时变系统，文献[17]指出线性时变系统的格拉姆矩阵比较繁琐，在实际工程应用中很难应用。随后，有个别研究学者将航天器自主导航系统近似化为分段线性定常系统(Piece-Wise Constant System,PWCS)，并根据格拉姆矩阵进行可观测性分析[18]，但是没有严格的证明。1992年，Goshen-Meskin和Baritzhack[19]证明了该方法的合理性，并将PWCS的可观测性矩阵称为提取可观测性矩阵(Stripped Obserbility Matrix, SOM)，当SOM为满秩时，称系统为局部可观的。他又将该方法应用于惯性导航系统的初始误差校准上，为了提高初始校准的有效性，在可观测性分析的基础上，对状态变量和状态空间进行选择和划分[20]。由于基于SOM的可观测性分析方法的简便易行，在航天器自主导航领域应用广泛。

2) 非线性系统

上述基于SOM的可观测性分析方法多以线性时变系统为研究对象。但是，由于受到航天器帆板或者大型天线挠性以及动力学之间的耦合特性等因素影响，是一个高度复杂的非线性动态系统。因此，有必要对非线性系统展开深入的可观测性分析研究。

由于非线性系统的动态行为与输入信号、初始条件以及状态位置密切相关，非线性系统的可观测性较为复杂[21]。在非线性可观测性分析方面，Hermann和Krener[22]做了很系统的研究工作，给出了非线性系统局部可观测性的充分条件。文献[23-24]在Hermann研究工作的基础上，采用李导数计算实现非线性系统的可观测性评价。但是由于该方法的计算复杂，更多的学者采用数值方法来分析非线性系统的可观测性。

为了避免李导数带来的复杂运算，一些学者从系统测量原理出发，通过几何关系来分析系统可观测性，并且在自主相对导航领域取得了一系列研究成果。文献[25]通过分析2个航天器之间的几何关系来判断轨道常值脉冲下的状态估计精度；文献[26]则在仅测角自主交会相对导航领域中，通过几何关系分析状态估计的协方差矩阵，并根据协方差矩阵的大小来制定自主交会策略。

可观测性分析虽然能够定性地分析系统实现航天器状态估计的能力，但是并不能够准确地评价能力的大小，因此需要进一步量化自主导航系统的可观测能力。

1.1.2 系统可观测能力量化方法

系统可观测性矩阵满秩与否可以判断系统状态是否可由系统观测来估计，但是实际的系统中并不总是直接表现出“可观测”或者“不可观测”，还常常表现为可观测程度极差的情况。在这种情况下，系统状态估计误差往往很大，甚至表现出发散的特性。因此，需要通过量化方法来了解系统状态能否通过观测量准确地估计。

系统可观测度量化最开始主要是从格拉姆矩阵非奇异的程度来量化系统可观测能力。主要是通过可观测矩阵的奇异值来进行判断。Müller和Weber[14]采用格拉姆矩阵的3个值来描述系统可观测度，即最小特征根、可观测性逆矩阵的迹以及行列式。最小特征根体现了系统可观测程度最差的状态变量；可观测性逆矩阵的迹体现了系统整体的可观测性，迹越大，系统可观测能力越强；可观测性矩阵行列式为零时，系统不具有可观测性，行列式越大，系统可观测性越好。但是，当任意特征值为零时，行列式也为零。因此，该方法具有一定的局限性。文献[27]利用条件数来量化系统可观测能力，即矩阵最大特征值与最小特征值之比。当条件数接近于1时，系统具备较好的可观测能力。

上述方法虽然能够在一定程度上能够部分或者完全表示系统的可观测度，但是无法表达每一个系统状态变量的可观测度。误差椭球是一种描述系统状态变量误差的直观方式，其来源于误差椭圆，表示的是随机变量的不确定性[28]。从可观测性矩阵的角度看，误差椭球的最长轴对应着可观测性矩阵的最小特征根。虽然三维误差椭球可以直观地表现出三维状态变量的可观测度，但是对于更高维的系统，无法直观地显示出系统状态变量的可观测度。麻省理工学院的Lee[29]证明了线性时变系统的格拉姆矩阵与Fisher信息矩阵[30]的一致性，并根据Fisher信息矩阵判断每一个状态量的估计精度。而在1946年Cramer[31]在其专著中首次提出了Cramer-Rao下界，用于量化状态估计值与已知误差统计特性的真实值之间的期望误差的下界，并阐述了其与Fisher信息矩阵的关系，因此Cramer-Rao下界成为了量化系统可观测能力的一种重要手段。对于非线性系统，一般通过李导数构建可观测性矩阵并量化系统可观测性。另外，可以对非线性系统进行线性化近似，结合Cramer-Rao下界量化状态变量估计精度，实现系统可观测性评价。Cramer-Rao下界由于可以有效地评价每一个状态变量的精度，所以在线性系统和非线性系统中均得到了广泛应用。

综合上述可知，系统可观测能力量化方法主要是从状态误差估计精度的角度，来判断或者分析系统实现状态估计的能力，直接影响着自主导航精度，并受到了航天器自主导航系统设计人员的重视。

1.2 导航滤波算法研究内容及现状

自主导航滤波算法主要是用于确定航天器的位置、速度及其他导航参数，通常选择航天器在轨的动力学模型或运动学模型为状态方程，导航敏感器的测量模型为测量方程。以卡尔曼滤波为代表的最优状态估计方法是导航滤波算法的基石[2]。针对航天器自主导航系统模型的特点，主要分为非线性滤波、鲁棒滤波及多信息融合滤波。

1.2.1 非线性滤波

如1.1.1节所述，航天器自主导航模型在大多数情况下为非线性模型。为了处理非线性模型，大多数研究学者主要采用线性近似法和粒子分布近似法来改进经典的卡尔曼滤波算法。

扩展卡尔曼滤波(Extended Kalman Filter, EKF)是最常用的非线性滤波算法。截取非线性系统模型泰勒级数的一阶展开项，实现系统模型线性化，再采用线性卡尔曼滤波算法结构，实现状态估计[32]。EKF虽然得到了广泛的应用，但是当非线性模型的高阶展开项无法忽略时，会产生较大的截断误差[33]，如图2(a)所示。针对这个问题，文献[34]结合高斯-牛顿方法实现系统状态的极大似然估计，进而提出了迭代EKF算法；文献[35]在EKF的基础上，采用拉格朗日优化技术，提出了一种二次状态等式约束的约束卡尔曼滤波算法，相比于EKF算法精度有了很大提升。另外，在航天器姿态确定系统中，受欧拉角万向节锁死现象，乘法扩展卡尔曼滤波(Multiplicative Extended Kalman Filter)被用来解决这一问题，但是不可避免地会出现因系统线性化而带来的误差影响[36]。以上这些方法在一定程度上提高了EKF算法精度，但是并没有从根本上解决截断误差问题。

由于近似非线性系统状态变量的概率密度比近似分布非线性系统模型更容易，基于采样点近似非线性分布的滤波算法得到了广泛关注，主要分为确定性采样和随机采样算法。粒子滤波(Particle Filter, PF)[37]是一种典型的随机采样滤波算法，利用参考分布随机采样大量粒子，然后将这些粒子进行非线性变化，利用一定的策略统计组合得到系统状态估计，如图2(b)所示。该方法虽然克服了EKF算法的局限性，但是需要大量随机粒子。这不仅增加了算法计算复杂度，还会产生粒子退化问题，引起滤波发散。目前已有一些降低粒子退化影响的方法[38-40]，但是都会带来更高的计算复杂度，难以星上自主实现。

图2 PF-EKF-UKF 3种滤波算法状态预测示意图[2]Fig.2 State prediction diagram of there filter algorithms PF-EKF-UKF[2]

相对于随机采样策略，确定性采样策略算法的效率更高，实时性更好。无迹卡尔曼滤波算法(Unscented Kalman Filter, UKF)[41]是一种广泛使用的确定性采样滤波算法，它是基于无迹变换采样策略近似非线性系统模型的滤波算法(如图3)。其计算精度至少可以达到2阶，采用一些特殊的采样方式可以达到3阶或者4阶，如单形采样[42]、偏度采样[43-44]等。因此，对于非线性较强的系统，UKF算法精度更高。但是从计算效率来看，相比于EKF算法，UKF算法还有待提高[45]。针对这个问题，文献[46]根据系统不同程度的线性和可分性等先验信息，归纳和构建了简化UKF算法，并详细分析了算法性能。除了UKF外，还有高斯和滤波(Gaussian Sum Filter, GSF)算法[47-48]、集合卡尔曼滤波(Ensemble Kalman Filter, EnKF)算法[49]等典型的确定性采样滤波算法，但是受星上资源限制，这些导航滤波算法在自主导航领域应用较少。

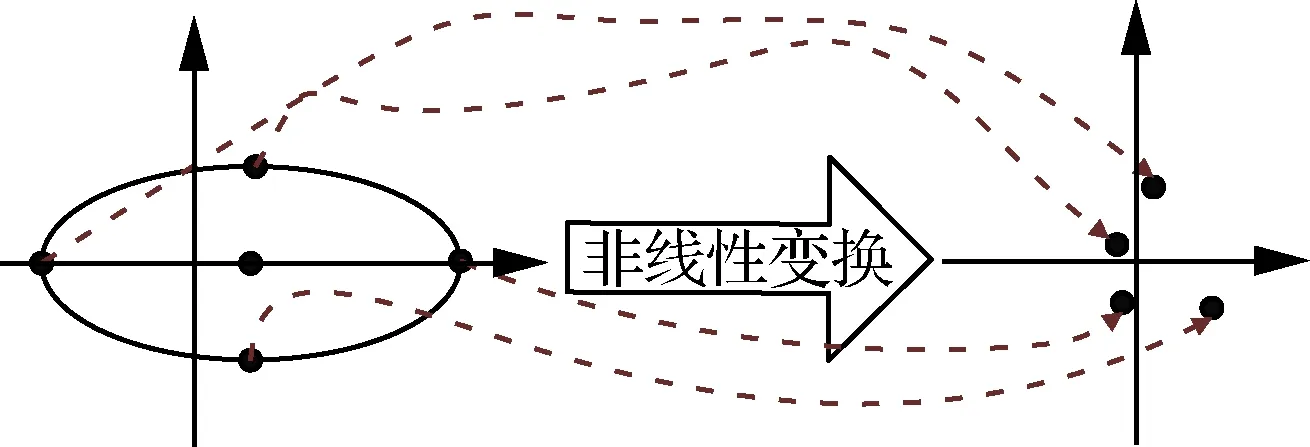
图3 Sigma点选取和无迹变换示意图[2]Fig.3 Sigma points selection and UT transformation[2]

基于采样策略的滤波算法虽然能够较好地提高状态估计精度，但是对于高维状态空间模型，可能会带来维数灾难问题[50]。为了避免这一问题，Arasaratnam和Haykins[51]提出了容积卡尔曼滤波(Cubature Kalman Filter, CKF)，采用三阶容积法则，利用数值积分来近似高斯加权积分，利用一组等权值容积点加权求和来代替高斯问题，从而实现状态估计，其计算量和精度与UKF算法相当。相比于UKF算法，CKF避免了因矩阵分解而可能出现的矩阵奇异问题，而且对于高维非线性系统，其状态估计精度更高。文献[50]经过分析对比得出：当系统状态维数大于3时，CKF算法的估计精度高于UKF算法。常用的非线性滤波算法性能特点如表1所示。

表1 常用非线性滤波算法的性能特点

上述滤波算法实现了大多非线性自主导航系统的状态估计问题，但是由于航天器在轨运行环境复杂，不确定性因素多，使得非线性滤波算法性能受到影响，这也推动了鲁棒滤波算法的兴起和发展。

1.2.2 鲁棒滤波

传统的滤波算法要求系统模型的形式和参数精确已知，系统噪声和测量噪声为零均值高斯白噪声。但是，在实际应用中，滤波模型与系统实际模型往往存在着一些差异，且实际模型往往受到众多不确定性因素影响，这种不确定影响因素会导致滤波算法精度降低，甚至发散[2]。在航天器自主导航系统中，X射线脉冲星星表误差、敏感器系统误差校正后残余以及未知摄动力模型等均可视为典型的不确定性影响因素。

为了解决不确定性影响问题，最常用的方法之一就是增广卡尔曼滤波[52](Augmented Kalman Filter, AKF)，即将不确定性模型参数扩充为待估状态变量，同原有系统状态变量一起估计，并利用估计值对系统不确定性进行在轨补偿。但是，当对系统状态模型扩维处理后，可能会因观测信息不足而导致系统状态不可观测。另外，即使可以实现模型不确定影响因素的估计和补偿，也会剩余部分残差，影响滤波精度。针对这些问题，自20世纪80年代以来，国内外研究学者开始研究关于克服模型不确定性影响的滤波算法，即鲁棒滤波算法。

鲁棒滤波算法最初的研究思路是根据实际系统中未知干扰信号的上界设计滤波算法[53]。在鲁棒控制理论的基础上，Grimble和Elsayed[54-55]根据系统噪声与状态估计误差之比的上界设计了H∞滤波。随着对鲁棒滤波算法研究的深入，近些年来许多学者关于不同类型的模型不确定性设计了不同的设计指标，如H∞范数有界[56]，参数范数有界不确定性[57]，状态估计误差方差上界最小等[58]，提出了多种不同形式的鲁棒滤波算法。但是H∞滤波的设计需要验证特定的存在性条件，而这种存在性条件往往难以验证。因此，该算法适用范围极其有限。规范化鲁棒滤波[59](Regularized Robust Filter, RRF)算法是一种不需要验证存在性条件的算法，其设计指标是使不确定性对测量残差的最大影响值最小化，其形式与KF算法类似，更易于被工程技术人员接受。

随着统计学的发展，基于稳健估计理论的鲁棒滤波算法逐渐成为研究热点。这类滤波算法主要是通过权重函数选择，最小化系统不确定性影响。Huber滤波算法[60]就是一种基于Huber权重函数的鲁棒滤波算法，通过对滤波新息截断平均来抑制不确定性误差影响。但是Huber权重函数会将一部分带有不确定影响的测量数据引入到系统中，降低状态估计精度。针对这一问题，在极大相关熵理论基础上[61]，陈霸东等[62]提出了极大相关熵卡尔曼滤波(Maximum Correntropy Kalman Filter, MCKF)算法。Principle[61]从信息熵理论的角度阐述了极大相关熵准则(Maximum Correntropy Criterion, MCC)权重函数的优势，即权重大小选取服从高斯分布。这使得MCKF在抑制不确定性影响时更贴近大多数实际情况，保留更多的有效信息并且较好地抑制了更多不确定性影响[63-64]。如图4所示，MCC即为MCKF对应的权重函数。

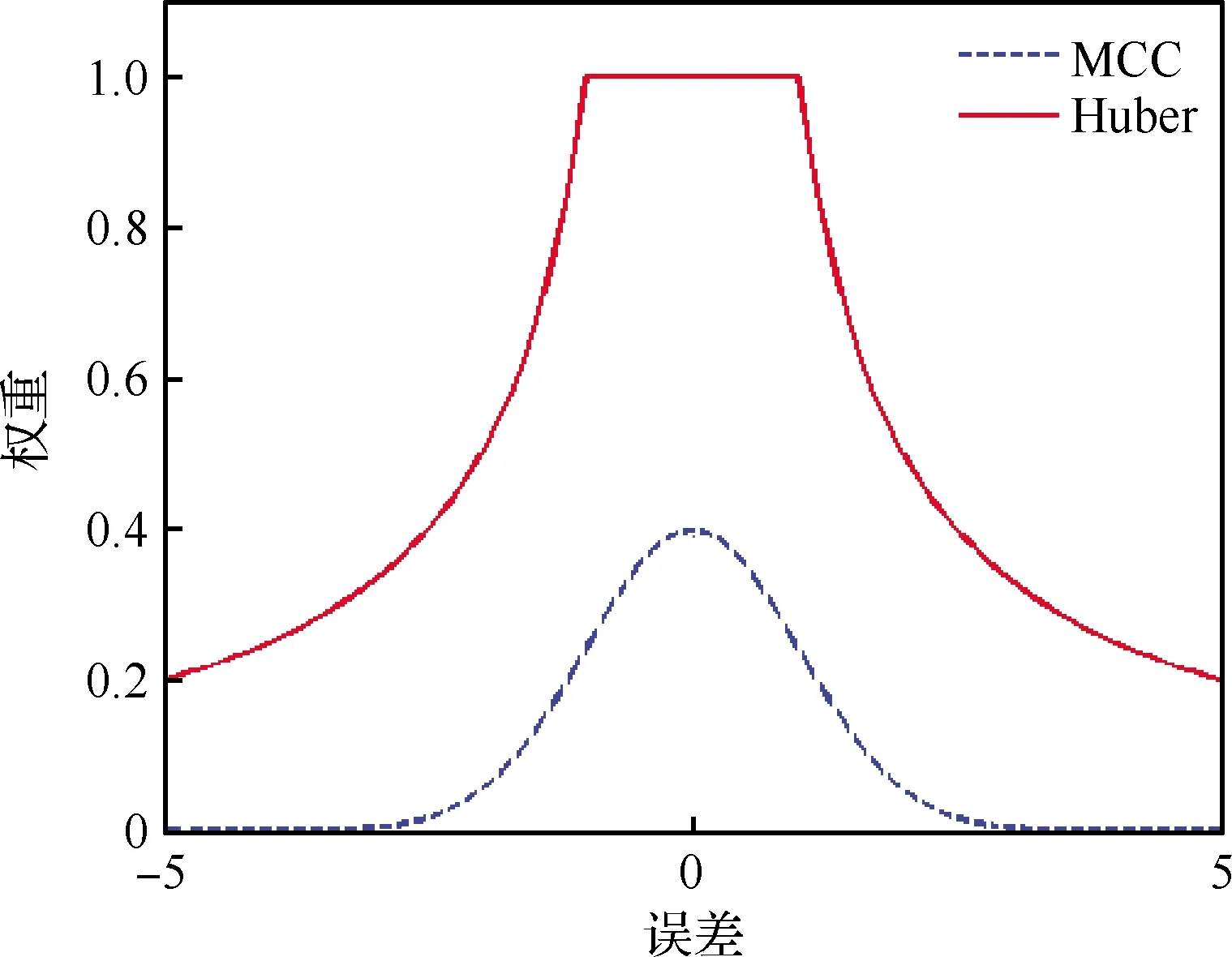
图4 不同误差影响下的权重函数Fig.4 Weighted function with different errors

上述方法可以有效地抑制测量模型不确定性带来的误差影响，但是不能克服状态模型不确定性影响。周东华[65]结合正交性原理提出了强跟踪滤波算法。这一算法使得残差在每一步都相互正交，并提取残差序列中的有效信息用于当前时刻的系统状态估计，有效地克服了系统模型不确定性带来的误差影响。

除了模型不确定性影响，噪声统计特性不确定性也是影响导航滤波精度的重要因素之一。Sage和Husa[66]提出了Sage-Huge自适应卡尔曼滤波算法，又称为方差匹配法。该算法结构简单，计算效率高，可以同时估计出系统噪声的一阶矩和二阶矩。在该算法的基础上，文献[67]提出了新的自适应滤波算法，用于未知统计特性噪声条件下的状态估计。

除了上述滤波算法以外，多模型滤波(Multiple Model Kalman Filter, MMKF)算法也是用于处理模型不确定性的算法之一。Magill[68]最早提出了多模型(Multiple Model, MM)算法，通过设定有限的模型集合逼近真实系统，基于每个模型的滤波器独立运行，最后对所有模型输出进行融合。但是，该方法没有考虑到模型之间的耦合性。文献[69]等基于伪贝叶斯算法提出了交互多模型卡尔曼滤波(Interaction Multiple Model, IMM)算法，对于混合系统的估计问题具有较高的状态估计精度；文献[70]提出了一种变结构(Variable Structure, VS)IMM算法来自适应调整模型集合，并根据测量值屏蔽或者去除与系统不相符的模型；文献[71]从加权Kullback-Leibler 散度(K-L 散度)出发，结合协方差交叉法，提出了一种基于信息理论的IMM(Information Theoretic Interaction Multiple Model, IT-IMM)算法，用于解决对目标运动状态不确定、噪声特性信息不足的问题，并且得到了较好的效果。

针对实际系统中的模型误差建立不确定性模型，进行鲁棒滤波算法设计，有助于消除或者抑制模型不确定性的影响，改善系统状态估计精度。

1.2.3 融合滤波算法

随着航天器导航敏感器技术的发展，现有航天器的测量手段也发生了变化，由单一的测量平台/系统向多源发展，也促进了多源信息融合滤波算法的发展[72]。目前的融合滤波算法主要都与融合结构有关，主要分为3类：集中式、分布式和混合式[73-76]。在航天器自主导航领域常用的是前2种结构，因此这里主要针对集中式和分布式融合滤波算法进行介绍[76]。

1) 集中式滤波算法

集中式融合滤波算法是利用一个中心处理器处理和融合系统所有敏感器量测数据。常见的集中式融合滤波算法包括：并行滤波、序贯滤波和数据压缩滤波。

并行滤波算法[76]是将所有敏感器的测量模型和测量数据组合作为伪测量方程、伪测量值，并将伪测量方程和伪测量值作为滤波输入，实现导航系统状态估计；序贯滤波算法是指按照敏感器的顺序对目标运动状态进行序贯更新，即在前一个敏感器数据导航滤波结果的基础上，利用当前敏感器测量数据再进行一次状态估计，直到最后一个敏感器，该算法实际上与并行滤波算法精度相同[77]；数据压缩滤波算法是指将测量数据划分，并且将测量数据和测量协方差用划分后得到的等效测量值和等效测量误差协方差代替，并通过滤波算法实现状态估计，该算法在功能上与并行滤波算法是等价的，但是对于同一划分的敏感器测量模型要求相同，极大地限制了算法的实用性[76-78]。

集中式融合滤波算法主要是针对在同一时刻各敏感器的测量噪声之间互不相关的情况。但是由于很多情况下离散异步多敏感器系统的测量噪声是相关或者耦合的，限制了相关算法的实用性。针对这一问题，也有相关学者对此做出了改进，包括面向相关测量噪声的集中式滤波[79-80]、基于运动学模型正则变换的目标跟踪算法[81]等。

2) 分布式融合滤波

分布式融合滤波算法是指：利用不同敏感器测量数据分别实现系统状态估计，再通过不同敏感器之间的关联进行融合得到最终的系统状态估计。最典型的分布式融合滤波算法是联邦滤波算法。

联邦滤波算法是由Calson[82]于1988年提出来的。它是通过合成每个敏感器的子滤波器的估计信息来实现状态估计的。其中，子滤波器是平行结构并采用KF算法来估计各自的状态量。另外，Calson为了避免各子滤波器状态估计结果的相关性影响，在方差上界技术的基础上，结合信息分配原则将系统噪声和全局状态估计结果分配给每个子滤波器，从而使主滤波器的融合结果与集中式融合估计精度一致。

联邦滤波算法不改变子滤波器算法形式，而且计算复杂度低、实现简单、信息分配方式灵活、容错效果好，因此，在基于多源信息融合的自主导航系统中受到许多关注。

1.3 系统误差补偿研究内容及现状

航天器自主导航系统误差是影响系统状态估计精度的主要因素之一。误差源主要包括测量随机误差和系统误差，测量随机误差一般可以通过导航滤波算法加以消除，系统误差主要包括测量偏差和安装误差等，是制约自主导航精度提高的主要瓶颈，如高轨卫星，40角秒的敏感器安装偏差将产生约18千米的导航误差。因此，实现自主导航系统误差的精确补偿是提高自主导航精度的一个主要途径。在现有导航敏感器性能水平和安装精度条件下，对系统误差进行建模和在轨补偿正是提高自主导航精度的重要手段[2]。

1.3.1 系统误差建模

要对系统误差进行校正，首先需要对其进行建模，要求模型尽可能精确地反映系统误差特性，并且形式简单、便于导航滤波器的设计。

地心方向系统误差建模方法[2]是成像式导航敏感器系统误差建模的主要方式。该方法是将成像式导航敏感器的系统误差(如标定残差、光学焦距误差、测量偏差等)统一描述成地心方向的旋转误差，有效地降低了状态变量的维数，有利于优化滤波算法结构，实现星上自主运行。

空间几何相位映射模型[83]是双锥地球敏感器系统误差建模的主要方式。该模型是利用地球椭球模型和扫描式地球敏感器测量原理构建的，再结合地平穿越点和高斯牛顿迭代法，确定实际扫描角、穿越点方位角和地心方向，实现地球扁率系统误差补偿。

傅立叶变换建模是周期性误差建模的主要方式。航天器恒星敏感器低频误差主要是由周期性的热畸变引起的，它对卫星姿态确定精度有很大的影响[84]。而傅立叶级数可以表征周期性信号，傅立叶系数可被假定为时间常数[85]。因此，在获得星敏感器测量数据和低频误差傅立叶级数模型的基础上，通过导航滤波算法，可以实现低频误差的估计。

1.3.2 系统误差补偿

在获得系统误差模型以后，需要通过系统误差补偿方法实现误差在轨精确补偿。目前主要的补偿方法有信息辅助校正、基于状态分离估计的系统误差在轨校正、误差分布估计补偿方法以及系统误差自校正方法。

信息辅助校正是指采用已知信息为基准，通过比对测量敏感器输出信息和已知信息，实现系统误差校正。如利用高精度成像设备对星敏感器误差校正[86]，通过将二者测量数据输出作对比，以高精度测量信息和星敏感器测量信息的差作为测量信息，再结合星敏感器系统误差模型，通过导航滤波算法实现误差估计和补偿。

基于状态分离估计[87]的系统误差在轨校正方法是指对系统状态和系统偏差进行分离估计，并同时利用估计偏差对状态进行更新。该方法操作简便，状态估计精度高。对于敏感器单一、误差模型简单的自主导航系统误差校正效果较好。

误差分步补偿方法[88]是指分步骤补偿系统误差，先补偿一部分系统误差，并在此基础上，补偿其余部分系统误差。该方法具有精度高、鲁棒性好的特点，能够满足光学敏感器系统误差在轨校正的需求。

系统误差自校正方法是指不依赖任何外部信息，仅利用导航敏感器观测量和系统模型，实现对系统误差的估计和补偿[2]。事实上，通过对系统误差补偿模型进行可观测性分析后，部分系统误差是可以在任何情况下实现自校正的，而另外一部分则需要辅助方式实现自校正。比如，对于偏心率不为0的航天器，地心方向测量的系统误差可以利用航天器轨道动力学信息实现误差自校正；当航天器轨道偏心率为0时，地心方向测量的部分系统误差存在不可观问题[89]，此时需要采用姿态机动辅助实现系统误差补偿[90]。

随着系统误差建模与补偿方法使用范围的不断扩展，学者对其研究也不断深入，并且逐渐地将二者结合起来应用于自主导航系统的误差校正中。

2 航天器自主导航状态估计方法应用现状

本节将主要介绍航天器自主导航状态估计方法的应用情况，阐述不同方法在航天器自主导航领域的不同应用背景。根据航天器系统应用场景，可观测性分析主要应用于近地航天器和深空航天器自主导航中；根据导航系统特点，导航滤波算法主要应用于非线性自主导航系统、不确定性影响下的自主导航系统、基于多敏感器测量的自主导航系统中；根据自主导航系统误差主要来源，系统误差补偿算法主要应用于导航敏感器的系统误差校正。

2.1 可观测性分析

由于可观测性分析方法主要以线性系统控制理论为研究基础，通用性较强，而且可观测能力的量化可以更好地评价不同自主导航系统方案的状态估计精度，因此已被广泛引入到航天器自主导航领域的系统方案评价应用当中。

2.1.1 近地航天器自主导航应用

可观测能力定性分析方法最早应用于自主导航系统的有效性分析中，利用其对导航方案进行评价，从而确定实现系统状态估计的可能性，并指导改进导航系统方案。

文献[20]基于PWCS可观测性格拉姆矩阵，研究了惯性导航系统在轨动基座校准过程中的可观测能力，并通过仿真分析证明了系统状态的可观测性。文献[91]将星光角距和星光仰角测量模型线性化，利用线性化观测矩阵构建可观测性格拉姆矩阵，给出了一种衡量天文导航系统中的观测量和系统性能的分析方法。文献[92]提出了一种基于恒星折射角的天文自主导航方案，通过分析系统格拉姆矩阵，讨论了恒星折射角观测的最佳方案，并通过实验说明了该方案可以显著提高导航性能。文献[93]将紫外敏感器引入到地月转移段轨道自主导航系统中，通过格拉姆矩阵分析可观测性证明了系统方案的可行性。文献[94]研究了基于星敏感器/卫星星间链路的航天器自主导航方案，并通过Cramer-Rao下界分析了该方案的有效性。

除了绝对导航领域，在自主相对导航系统中，基于格拉姆矩阵的可观测能力定性分析方法也得到了广泛应用。德宇航(German Aerospace Center, DLR)[95]在PRISMA任务设计中[96]通过格拉姆矩阵分析指出，通过轨道机动可以改善仅测角相对导航系统可观测性，并实现空间非合作目标自主相对导航系统状态估计。在DLR的研究基础上，斯坦福大学[97]将J2摄动项引入到仅测角相对导航系统模型中，并通过格拉姆矩阵分析证明了该系统方案在部分轨道构型下的可行性。文献[98]通过格拉姆矩阵分析了基于相机偏置的仅测角相对导航方案的可行性，并给出了系统可观测能力的解析模型，实现了状态估计性能的评价。

格拉姆矩阵主要用于线性系统模型或者近似分段线性定常系模型的可观测性分析，而基于李导数的可观测性分析主要应用于非线性系统。文献[99]在多卫星系统自主导航研究中引入相对位置测量，并利用李导数证明了系统局部弱可观的充要条件。文献[100]提出并通过李导数证明了基于视觉/惯性/地磁敏感器自主导航系统的可行性，并通过仿真验证了可观测条件的正确性。

2.1.2 深空航天器自主导航应用

随着中国在深空领域自主导航任务需求越来越多，可观测性分析也起到了至关重要的系统评价作用。

文献[101]提出了基于惯导/卫星/火星陆标的火星进入段自主导航方法，采用格拉姆矩阵的秩和条件数分析了系统方案的可行性；采用Fisher信息矩阵评价系统可观测度，并说明采用2个卫星和2个火星陆标就可以满足火星进入段自主导航精度需求。文献[102]建立了深空自主导航系统观测模型，并在李导数的基础上，提出了一种基于位置确定精度和可观测性秩条件的系统可观测能力定性分析方法。文献[103]在小行星探测自主相对导航任务中，基于李导数可观测性分析方法，结合仅测角相对导航模型构建系统可观测性判据，给出了实现仅测角相对导航状态估计的条件。文献[104]提出了基于序列图像的火星着陆段自主导航方案，结合格拉姆矩阵分析得出，在惯导信息辅助的情况下，连续两个序列图像可以实现状态估计，并通过可观测性矩阵的零空间分析证明了着陆器水平方向位置状态量和俯仰角状态量不可观。文献[105]提出了一种月球探测器环月段自主天文导航系统，以月球-探测器-恒星、月球-探测器-太阳这2个位置面和月心距作为观测信息，结合可观测性格拉姆矩阵的秩、特征根以及误差协方差阵阐述了自主导航方案的可观测能力。

综上分析可知，可观测性分析目前主要是从测量数据能否支持实现状态估计，并没有将系统计算能力、资源约束、环境约束等影响作为评价条件之一。因此，在对导航方案可观测性分析时，还需要从系统层去评价。

2.2 导航滤波算法

导航滤波算法是实现状态估计的核心手段，对于航天器实现自主导航具有至关重要的作用。目前，针对航天器自主导航系统的特性、在轨运行环境影响，通常采用不同类型的滤波算法实现状态估计。

2.2.1 非线性自主导航系统应用

由于航天器自主导航系统大多数属于非线性系统，因此，非线性滤波算法应用较为广泛。这里将阐述非线性滤波算法在自主导航领域导航领域中的几个典型应用。

EKF滤波算法由于不需要利用粒子采样来近似非线性模型，计算效率较高，在自主导航领域相对来讲应用最为广泛。其最早应用于美国的“星尘”(STARDUST)号探测器[106]来处理光学成像测量信息，实现探测器位置状态估计。另外，基于EKF的姿态确定方法也被经常应用于航天器姿态控制系统中，包括美国哈勃太空望远镜[107]、日本的先进陆地观测卫星[108]等。国内的相关研究机构和学者也开始将EKF算法应用于自主导航系统中。文献[109]采用基于地球规则地貌目标观测信息的近地航天器自主导航与姿态确定方案，利用EKF算法实现了航天器自主位置确定和姿态确定。文献[110]考虑到EKF算法的计算效率高，利用EKF实现基于太阳矢量-径向速度-地球矢量的深空自主导航状态估计

为了克服线性化误差影响，基于粒子采样的UKF和PF算法逐步被应用于航天器自主导航系统状态估计中。

UKF算法最早于2007年应用于美国海军研究生院航天器结构与技术卫星[111](Naval Postgraduate School Spacecraft Architecture and Technology, NPSAT1)上，它通过处理卫星磁强计测量信息来获得卫星姿态及其变化率的估计值，实现卫星姿态确定。加拿大NGC航空有限公司[112]将UKF算法应用于普罗巴2号(PROBA-2)卫星探测器，实现其轨道状态和姿态估计。

PF算法由于计算效率较低，难以星上自主运行，目前在自主导航任务中应用较少。但是国内外相关学者已经开始研究将其应用到自主导航系统中。文献[113]将PF算法应用到简易的非线性自主组合导航系统，并用其处理非高斯噪声，从计算结果来看，该算法性能较好，计算负荷较低；文献[114]为了克服PF算法的退化问题，将无迹变换引入到粒子滤波重采样中，并将其应用于天文/多普勒自主导航系统中，采用航天器实测轨道数据验证了该算法可行性。

由于CKF算法在高维状态估计中的精度优越性，目前也开始应用在自主导航领域。文献[115]将CKF算法用于基于地形重建的自主导航中。另外，国内学者也研究将其应用于基于太阳-地球-月亮信息的自主天文导航系统中[116]，并通过仿真证明其相对于UKF算法的优越性[50]。

2.2.2 不确定性影响的自主导航系统应用

为了克服工程应用中模型不确定性问题，鲁棒滤波算法开始逐渐应用于自主导航系统状态估计中。

文献[117]研究了基于H∞滤波理论的相对导航算法，并将其应用于追踪卫星相对导航应用背景中。在追踪卫星大轨道机动的情况下，能够有效抑制模型不确定性和非高斯噪声对系统造成的影响。文献[118]将Huber滤波应用于编队飞行的相对位置、速度和姿态的估计，在非高斯噪声的条件下，该滤波方法相对于EKF算法可以获得更高精度的状态估计结果。文献[119]研究在六自由度椭圆轨道的交会对接中采用Huber滤波算法，并且通过数值仿真证明鲁棒滤波器可以估计非高斯噪声下的噪声协方差。文献[120]将UKF算法与MCKF算法相结合，用于非线性航天器自主相对导航系统中，实现了在重尾分布噪声影响下的高精度状态估计。

针对自主导航系统中的状态突变情况，文献[121]利用STF滤波实现了基于紫外敏感器自主导航系统的状态估计，而且在系统出现渐变故障或者突变故障时，算法仍能工作正常且处在最佳状态。文献[122]将自适应滤波算法应用到自主卫星导航系统中，利用衰减记忆法实现噪声统计特性估计，有助于航天器自主能力和控制精度提高。

对于模型不确定性的自主导航系统，MMKF也是行之有效的一种方法。文献[123]在处理星敏感器姿态确定过程中的低频误差时，利用MMKF算法实现了误差信号的幅值与特定频率的识别，从而得到一个参考模型来补偿低频误差的影响。除此之外，MMKF还被应用于在卫星姿态低频误差估计与补偿[85]、卫星自主定轨系统[94]以及火星探测任务巡航段的自主导航系统[124]中。

2.2.3 基于多敏感器测量的自主导航系统应用

随着测量敏感器技术的发展，航天器逐渐配备了多种敏感器实现测量数据获取。为了实现基于多敏感器信息融合的高精度状态估计，融合滤波算法也开始逐渐被应用于自主系统中。

文献[2]将联邦卡尔曼滤波算法应用于卫星姿态确定系统中，通过信息因子分配，实时确定星敏感器、红外地平仪、太阳敏感器等测量信息的融合规则，实现了基于多敏感器信息融合的卫星姿态高精度估计。文献[125]在地月转移段采用联邦UKF算法实现月球探测器位置和速度的状态估计，通过子滤波器过程噪声和状态估计协方差实现信息因子分配，有效地提高了状态估计精度、鲁棒性和可靠性。文献[126]在X脉冲星/紫外敏感器的组合导航系统中采用联邦滤波算法有效地提升了自主导航状态估计精度，导航系统性能相比于普通滤波算法有了明显提高。

2.3 系统误差补偿应用现状

系统误差建模是误差补偿的关键一步，通常往往结合系统误差补偿算法共同实现系统误差估计和校正，从而提高状态估计精度。目前关于系统误差补偿的应用主要是针对于自主导航系统敏感器误差。

文献[90]将紫外敏感器的系统误差转化为地心方向矢量误差，并结合偏航姿态机动辅助，提高系统误差状态变量的可观测性，结合EKF算法，实现了测量偏差的估计与自校正，并显著提高了紫外敏感器自主导航系统的导航精度。文献[127]通过构建地球敏感器误差的空间几何相位映射模型，分析不确定性脉冲信号影响机理，抑制其对卫星姿态测量的影响。文献[128]将陀螺漂移与星敏感器低频误差表征为傅立叶级数，在此基础上，建立了低频周期误差补偿模型，提高了姿态测量精度，实现了高精度卫星姿态确定。

在测量信息足够的情况下，误差参数可观测性较好，通常可直接通过误差补偿算法实现系统误在轨校正。文献[129]在自适应两级UKF算法的基础上，通过衰减因子补偿模型的不确定性，分离估计系统状态和偏差，并将其应用于存在随机时变偏差的近地卫星自主导航系统状态估计中，有效地实现了导航系统误差精确补偿和高精度状态估计。

当状态变量与系统误差存在耦合，不易分离时，通常单独估计误差参数，从而实现误差精确补偿。文献[130]首先采用简化反向传播神经网络对光学相机的焦距和主点进行参数估计，然后用UKF算法对畸变等参数进行精确标定，该方法具有自初始化的优点，不需要姿态或预先安装的传感器参数，满足大多星载相机在轨校正需求。文献[88]采用基于最小二乘和卡尔曼滤波的迭代算法，实现了星敏感器非线性畸变的分步校准：首先通过迭代算法求得最优焦距和主点，然后在此基础上求解高阶焦平面畸变，实现了星敏感器误差精确补偿。文献[131]在一个由外部参数决定的广义摄像机框架中，进行逐步校准，分别实现光学相机的外部参数和内部参数高精度估计。文献[132]提出了一种基于GPS数据辅助的自主校准方法确定。分析和仿真结果表明，与基于轨道数据的标定方法相比，基于姿态数据库的标定方法可以直接、准确地估计传感器的测量误差。基于GPS的自主标定方法可以同时估计轨道状态和误差系数。该方法有利于自主运行，适用于传感器测量误差的在线变化。而且在没有GPS数据时，可用天文导航数据代替。

3 航天器自主导航系统状态估计发展趋势

从技术发展趋势来看，状态估计方法的改进是提高航天器自主导航精度的一种重要途径，具有良好的发展和应用场景。目前国内外学者从不同角度、不同应用、不同领域对航天器自主导航系统状态估计进行了探索和研究，在各关键技术方面都取得了一定进展。但是，航天器自主导航状态估计方法仍存在较多难点问题未能很好地解决，其难点问题主要有：针对星上计算资源严重受限的约束，如何构建自主导航系统的可观测度评价体系；针对多维多时空导航信息，如何设计快速可靠的融合滤波算法；针对系统多源误差影响，如何实现基于统一建模的系统误差快速估计与补偿等。因此，需要针对上述难点问题深入开展研究，以满足航天器自主导航任务的需求。

3.1 航天器自主导航系统的可观测性评价体系

尽管国内外相关研究通过可观测性格拉姆矩阵、Fisher信息矩阵等方法，经过一系列的改进和完善，构建了关于实现导航系统状态估计的可能性或者状态估计精度的评价标准，但是大多以高维的有限阶可观测性矩阵运算为基础，没有将航天器有限的星上资源考虑在内，特别是多源导航信息处理会占用大量的星上存储资源和计算资源，严重影响航天器自主运行能力，增加星上存储和计算负担，因此需要解决如何将航天器自主运行能力考虑在内，从系统层面构建可观测性评价体系。

另外，系统可观测能力的分析还可为导航系统的状态完备估计和误差参数的精确估计与补偿提供指导，优化滤波算法结构，加快滤波收敛速度，降低星上计算压力。因此，还需要解决导航系统状态变量和误差参数的可观测能力表征问题。

3.2 多源信息条件下的快速融合滤波算法

从目前的研究情况来看，要实现航天器自主导航状态估计，尤其是对于未知环境下的导航任务，自主导航系统通常还需要融合惯性测量单元、测距测速敏感器、光学敏感器等其他外部敏感器的测量信息以提高导航系统精度和可靠性，这就需要解决测量信息的融合问题。

针对自主导航任务过程中的惯性测量、测距测速信息和光学图像信息等导航信息时间不同步、空间不一致等问题，需要研究多源测量信息的时空同步与表征方法。另外，考虑到星上计算资源有限，为了满足航天器自主运行的需求，需要在可观测性评价体系指导下，解决如何选取高质量测量信息才能满足自主导航参数估计的需求、如何设计滤波算法才能有效提高状态估计效率等问题。

3.3 基于统一建模的系统误差快速估计与补偿

目前，国内外学者在系统误差建模、误差补偿算法的研究方面已经取得了一定的进展和效果。但是，对于基于多敏感器融合测量的自主导航系统，敏感器误差来源广、影响机理差别大，航天器在轨环境不确定因素多，已有的误差精确补偿方法还无法实现多源系统误差的精确建模与补偿。

针对航天器自主导航多源误差和不确定性影响导航精度的问题，需要从误差机理、误差表征和误差传播等方面来分析误差对状态估计的影响，研究构建误差响应函数，解决如何构建误差对状态估计精度影响解析模型的问题；针对系统测量信息有限的问题，借助于导航系统可观测性评价体系，需要研究能够表征所有误差影响的参数模型，解决如何选取待估参数才能尽可能精确补偿全部误差、优化状态估计参数结构、实现系统误差快速估计与补偿等问题。

4 总结

航天器自主导航系统的状态估计是未来实现航天器自主运行任务的重要技术手段之一。本文首先对于自主导航系统状态估计方法的研究现状进行了总结，然后概括并分析了状态估计方法在航天器自主导航任务或者研究中的应用，最后对航天器自主导航系统状态估计方法的难点问题进行了总结分析，并对其后续发展进行了展望。

当前，航天器自主导航技术发展十分迅速，为了提高自主导航精度，美国等航天强国对状态估计方法都在积极开展研究，并取得了一系列成果。中国正走在从航天大国向航天强国迈进的进程中，将要把航天器自主导航技术应用在高轨卫星、空间操作平台以及深空探测等领域中，因此有必要对状态估计方法进行更为深入的研究，为中国未来航天器自主导航任务提供必要的技术保障。