基于卷积神经网络的深度学习流场特征识别及应用进展

叶舒然，张珍，王一伟，黄晨光

1. 中国科学院 力学研究所 流固耦合系统力学重点实验室，北京 100190 2.中国科学院大学 工程科学学院，北京 100049

特征识别作为一类通用的数学物理问题，由于自身的复杂性，一直是一个需要解决的热点问题。其中，降阶模型(Reduced Order Models，ROM)作为一种特征识别方法，已被证明是减少完整动力学系统的复杂性和大尺寸的强大工具[1]。在流体力学领域，本征正交分解(Proper Orthogonal Decomposition，POD)方法作为一种基于模态分析的典型降阶方法，能够针对流场的识别问题捕获不同的流动特征[2]。Berkooz等[3]开始将POD方法用于湍流中，Ravindran[4]提出了使用POD降阶的方法进行流动控制。Wu等[5]构建了基于POD方法的外形优化方法。除了POD等模态分解的降阶模型方法以外，针对涡旋辨识，Dubief和Delcayre[6]提出基于Q2不变量的Q准则能够显示出很好的相干涡旋， Xiong和Yang[7]提出了涡面场构造算法。这些传统方法均取得了一定的成果。

随着计算机和大数据领域的发展，近年来深度学习在语音识别[8]、图像识别[9-12]、自然语言处理[13]、自动驾驶[14]等方面的应用有了飞速的发展。这种背景下，流体力学领域也逐步开始了一些深度学习应用的尝试。早期主要是一些关于湍流中雷诺应力闭合模型的尝试，Tracey等[15]利用单隐层的神经网络拟合雷诺平均纳维-斯托克斯(Reynolds Averaged Navier-Stokes，RANS)湍流模型；Ling等[16]提出使用嵌入伽利略不变性的多层网络预测雷诺应力张量；Wang等[17]从高保真直接数值模拟(DNS)数据中基于机器学习方法重建了RANS模拟的雷诺应力中的差异；这些在高保真数据驱动下借助神经网络对雷诺应力进行建模的方法提高了原始模型的精度[15-18]。湍流建模中成果的积累也启发了流体力学中其他问题和深度学习结合的尝试，包括降阶建模、实验数据处理、形状优化[19-20]和控制等[21]。这些问题也可根据算法进行分类，例如以长短期记忆网络(Long Short-Term Memory，LSTM)为代表的循环神经网络(Recurrent Neural Network，RNN)的时序模型在结构的动态响应[22]，流体流动的时间演化[23]等。

流场识别作为流体力学一个专门研究问题，近年来也在理论验证、建模、优化等应用上和深度学习结合。以卷积神经网络(CNN)为首的深度学习网络模型能够对流场进行较好的特征识别与降维操作。降维后的特征在能够进行量化和可视的同时，也经常被用于预测和优化最佳设计等问题中。需要大量仿真来分析模型参数的原始问题经过了特征识别和降维操作后能够在极大地提高计算效率的同时保持一定的精度。此外，对于生成类问题应用而言，生成模型的输入采用的是特征信息。例如，以U-net为代表的网络结构中，原始输入经过多层卷积后得到的特征同时作为生成模型的输入信息，而并非简单的数据下采样。这种基于流场特征的生成类模型为分辨率提升等应用提供了依据。含有卷积神经网络的流场识别模型在不同类型的应用中均起到了关键的作用，在计算量和精度方面体现了巨大的优势。

1 卷积神经网络

深度学习的发展带来了神经网络种类的不断提升，其中卷积神经网络是一类适合对网格数据进行处理的算法[24]，目前已经很成熟地应用在图像识别等领域。卷积神经网络主要是由卷积层和其他连接层构成，其中卷积是一种加权平均的数学运算，权重函数为w的表达式通常表示为

s(t)=(x*w)(t)

(1)

式中：卷积中的函数x通常被称为输入；函数w被称为核函数。在实际操作中，考虑到离散项以及用于二维卷积运算的二维核，该表达式可以写为

s[i,j]=(I*K)(i,j)=

∑m∑nI[m,n]K[i-m,j-n]

(2)

式中：I为二维图像输入；K为二维的核。

对于传统全连接网络，每一个输出单元都与输入单元通过参数形成交互，而对于卷积神经网络，由于核(Kernel)大小远小于输入大小，因此带来了卷积神经网络中稀疏连接和参数共享两项改进。等变表示则是通过池化层(Pooling Layer)实现系统的另一项效率改进。池化操作使网络的输出被相邻输出的总体统计特征所代替，例如最大池化(Maxpooling)操作提供了目标位置范围内的最大值。

基本卷积层以不同的规模和方式相连接，发展出了许多不同的经典网络模型，例如AlexNet[9]、GoogLeNet[10]、VGG[11]、Resnet[12]等。除了网络本身的架构以外，训练时的梯度下降等方法以及超参数的选取也对模型结果有着重要的影响[25]。这里对上述网络细节不做过多关注，只从网络层基础类别的角度进行分类讨论。

如图1所示，文中所涉及的网络都是由卷积模块和不同的后续网络结构构成的。在上述及后续的讨论中可以明确卷积层在整体网络中起到特征识别的作用。流场信息经过卷积层的卷积操作得到流场特征，因此对于含有卷积网络的结构模型，可认为是带有与特征识别相关的部分。不同通路之间的区别来自后续网络层对提取出特征信息的处理，因此网络划分成以下3个主要结构：① 流场提取出的单个或多个并列信息，认为是所提取出的特征降阶；② 特征和所关心的流场信息通过网络联系，形成映射，达到通过流场对关心量的预测；③ 借助U-net等网络结构先对特征进行提取，但与此同时更关注将网络从低分辨率映射产生高分辨率的输出部分，是一类生成类的问题。以上这些问题中卷积层都起到了非常重要的作用，不同的网络结构使得对卷积提取的特征的扩展研究十分全面。

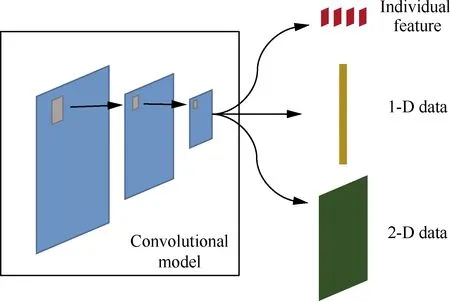
图1 基于卷积模块特征识别的各类网络结构Fig.1 Architecture of different networks based on convolutional model for feature detection

根据上述对网络结构的分类讨论，下文分别从不同的网络结构对流体力学中包含特征识别模块的3类问题进行介绍。第2节介绍了流场识别问题中作为基础的特征识别和降阶模型的构建；第3节介绍了以一维流场特征量为代表的流动预测和优化类问题；第4节概述了目标为高维数据的流场数据的生成类问题；第5节对本文进行了总结，对重点问题进行了进一步的思考与讨论，同时提出了对未来研究的展望。

2 特征识别与降阶

在流体力学中，特征识别是受到广泛关注的一类问题。现有的特征识别方法主要是通过局部场数值的识别，这些方法存在一定的局限性，以Q准则为例，其识别结果受主观阈值影响较大。

除了上述传统方法，近年来流场特征识别研究也开始出现部分基于深度学习的方法。Liu等[26]使用了一种基于CNN的激波检测方法，使得最终的网络能够找到激波位置。该方法与之前Lovely和Haimes[27]未使用深度学习算法的工作相比，在计算时间上有了较大的提升。Zhang等[28]基于CNN实现了具有快速响应的瞬态流动状态识别，可以立即识别出分离流等区域，识别精度高达94%。魏晓良等[29]提出了一种基于CNN提取特征结合LSTM学习时序信息的空化识别方法，准确率高达99.5%。Strofer等[30]提出了一种基于R-CNN的流场识别特征方法，通过流场中对网络的训练，在二维流动中的回流区域和边界层，和三维流动中马蹄涡的识别上都得到了成功的应用(图2)。这种数据驱动的特征识别方法能够很好地利用其泛化能力，相较于基于给定物理准则的识别方法而言能够更好地检测出未知特征。可以认为，基于深度学习的特征识别方法在精度和时间层面上都存在一定的优势。

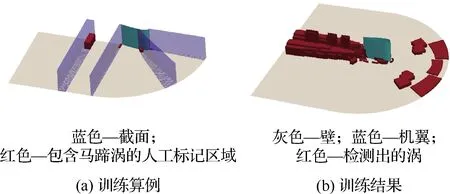
图2 训练算例和结果[30]Fig.2 Training cases and results[30]

深度学习方法在流场识别问题上能够有成功的表现归因于深度学习能够正确地对流场进行特征提取。流场特征识别作为一种降阶方式，一直是流体力学中关注的问题，多年来已经进行了一定的研究。目前应用于流场特征的降阶方法除了以Volterra级数模型[31]和ARMA模型[32]为例的基于信号的降阶方法外，基于流场特征模态的POD也是主要的降阶策略[33]。POD方法在翼型流场等方面有着丰富的应用[34-36]，也有着一系列的扩展和新颖的降阶策略，被许多案例证明是一类成熟的方法。

由于POD在降阶方法中的出色表现，一些流场识别问题中考虑到使用以POD为代表的模态分解与基于深度学习的回归分析相结合的方法。Liu和Wolf[37]提出了通过POD的流动模态分解以及深度前馈神经网络(Deep feedforward Neural Network, DNN)进行的回归分析方法，这种适用于不稳定可压缩流动ROM的构造方法证明了深度学习参与构造ROM的鲁棒性。Wu等[38]同样通过正交分解生成流场的基函数作为流场的低维特征，而作为卷积神经网络的变体之一的时间卷积网络(TCN)用于对低维特征进行时间序列建模，这种模型简化方法在圆柱绕流的算例中的计算时间相较于传统数值模拟减少了3个数量级，证明了该方法的高效性。Miyanawala和Jaiman[39]同样用正交分解技术将数据投影到低维的空间后，利用CNN中带有非线性激活的线性卷积层自动提取低维的特征的优势，预测下一时间步下流场POD的时间系数，证明了该类方法在长期流场预测的稳定性。可以认为，深度学习网络的参与使得原始方法中鲁棒性、高效性和稳定性得到了提升。

上述降维和动力学相结合的方法虽然涉及了深度学习的使用，但更多的是利用了深度学习算法回归分析的能力，流场的低维表示则是由POD等传统方法完成。从深度学习自身的角度出发，以CNN为首的神经网络本身已经是一类能够进行图像识别的算法，本文不满足于借助传统方法的处理而是思考单独的深度学习方法是否也能达到特征识别的效果。

Renganathan等[40]采用深度神经网络构造了降阶模型，这种方法能够以更小的计算代价达到相同的精度，这也是使用神经网络降阶的重要特点。注意到文中采用的方法是带物理约束的，不过更多情况下早期深度学习方法利用的是数据驱动思想。Wang等[41]使用神经网络构建了对细网格到粗网格解的特征的映射，多层神经网络利用激活函数识别并选择最重要的多尺度特征。Pawar等[42]提出了一种数据驱动下的流体降阶建模框架，结果表明基于DNN的模型能够较好地数值预测动态系统的演化，同时也提出了对于复杂流动的降阶建模的思考。由于作为模型识别阶段的POD可以类比浅层自动编码器，所以深度神经网络在不依靠POD进行前处理的情况下依然能够提供高维数据的简单表示。DNN也可以从snaphsot数据中学习潜在的低维流形[43]。Han等[44]将深度学习技术用于流线的特征学习。基于编码解码网络提出的FlowNet，能够学习到流线和流面的潜在特征。

含有编码解码的基础自动编码器是由全连接网络构成的。在上述的工作中虽然被证明具有一定的特征识别能力，但对于复杂数据而言，一维的全连接层不能发挥出较好的作用。因此，在网络结构中引入卷积层能够使网络更好地学习到数据的复杂表示，同时卷积网络自身的参数共享的特点也能够使得网络需要学习的参数减少。Omata和Shirayama[45]提出了一种流场空间结构的低维特征表示方法，使得非定常流动在特征空间可视化。Fonda等[46]将Rayleigh-Bernard对流中的数据通过U-net将数据压缩了5个数量级。Lore等[47]证明了堆栈卷积自动编码器能够为动态网络提供较LSTM网络更好的分布。Kim和Günther[48]利用卷积神经网络进行了过滤和特征提取两个步骤，显示了深度学习在预处理和特征提取两个方面组合中的巨大潜力。从另一个角度考虑，对于深层DNN而言，用于类比POD的浅层编码和回归分析从网络结构上难以区分，而卷积神经网络除了参数上的特点以外，另一个因素更是卷积算子(过滤器)在算法上能进行特征提取的优势。

对于CNN能够进行特征提取的过程，图像识别领域从卷积过程可视化的角度给出了说明[49]，认为训练过程中特征能够对特定特征图(Feature Map)进行激活。此外，从流体力学角度同样给出了对CNN特征降阶结果十分巧妙的理解方式。Murata[50]提出了使用卷积神经网络对流场进行分解，并且把分解的结果和POD算法进行对比，发现经过卷积网络分解的流场包含多个POD模态中的正交基(图3)。同时，模式分解卷积神经网络(MD-CNN-AE)中由于非线性激活函数的使用，使得MD-CNN-AE的重构误差比POD低。因此认为带有CNN的分解比标准的POD算法具有更低维度的特征提取能力，同时在可解释性上也得到了一定的验证。

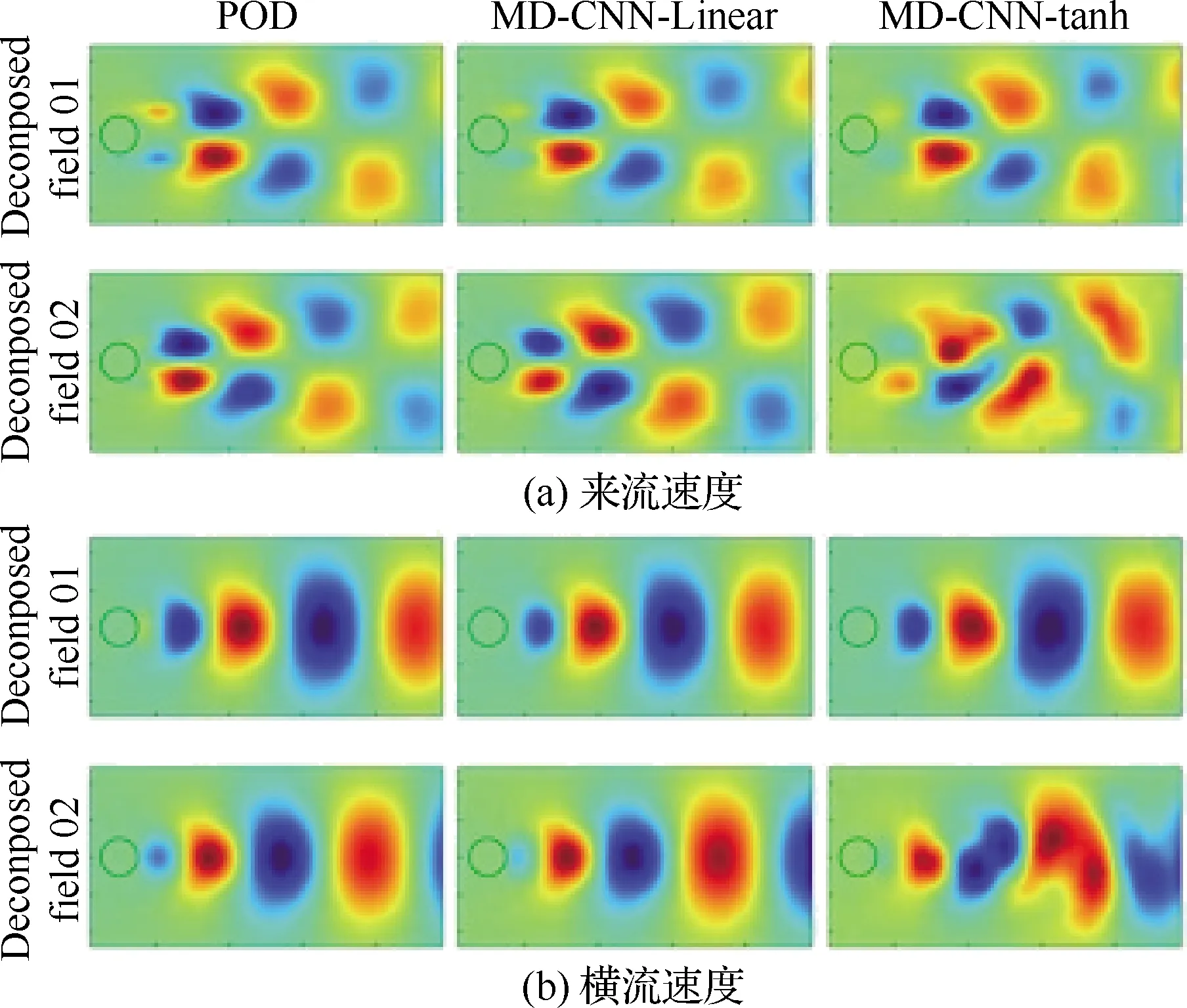
图3 POD、MD-CNN-Linear和MD-CNN-tanh 分解的流场[50]Fig.3 Decomposed flow fields with POD, MD-CNN- Linear, and MD-CNN-tanh[50]

3 流场预测与优化

流场经过卷积提取出特征之后，一个重要的关于特征的深层次运用是将其和流场一维关心量相联系，例如从流场速度场中卷积得到的信息与流场结构的表面压力系数关联，以达到后续预测以及带目标优化的目的。

3.1 流动预测

在许多数据科学的领域，深度神经网络都被证明具有学习变量之间复杂非线性关系的能力。Hadikhani等[51]从图像的角度出发，基于深度神经网络通过观察液滴形成的过程预测出了流速和浓度的流场信息。Tenney等[52]使用DNN网络，构建了一个对于超声速射流的远场的压力波动的预测网络，能够成功预测远场定向总声压级(OASPL)且在平均水平上优于传统的模型。

对于许多流体问题而言，CNN在具有同样预测能力的同时，比其他网络具有一定的优势。Chang和Dinh[53]利用不同的深度学习模型进行了热流体仿真中的预测，除了不同物理集成机器学习框架的区别研究之外，文中强调相较于前馈神经网络，基于CNN的闭合模型具有更高的可预测性。Fukami等[54]加上了与随机森林和支持向量回归的机器学习算法对比，在考虑的二维或者三维流动问题中，卷积神经网络的超分辨率分析能够应对大数据中维度灾难。因此，在利用深度学习方法时，对于所需要探索的流体动力学问题，考虑选择正确的网络模型是优化准确度和降低计算成本的关键。

对于根据已知几何外形预测速度场或压力系数类的问题，CNN的结构表明它是一类符合流体参数预测需求的算法。一个主要原因是由于CNN借助能够特征识别，把握流场中更主要的信息。Miyanawala和Jaiman[55]采用卷积对钝体的几何形状进行了操作，得到形状与流体力之间的映射，表明了基于CNN 的学习能够以少量的输入输出精确捕捉与流场力有关的特征。Bhatnagar等[56]证明了CNN能够在最少的监督下自动检测基本特征，因此，在给定雷诺数、攻角和翼形的情况下能够有效预测气动流场中的速度和压力场。Ye等[57]从速度场信息中得到流动特征，在不同的流动工况之间进行迁移学习，能够在维持精度的同时大大缩短网络训练时间，为算例的推广和泛化提供参考。对于在时间序列上的波动，CNN同样能够以卷积的方式学习到其在时间序列上的特征。Jin等[58]通过对圆柱体表面压力系数波动时空信息的捕捉，建立了圆柱表面压力脉动和其周围速度场的映射成功推测出尾流的速度场。结果表明，基于CNN的Cp-u模型预测的尾流速度和涡量与CFD所获得的速度和涡量具有很高的一致性(图4)。

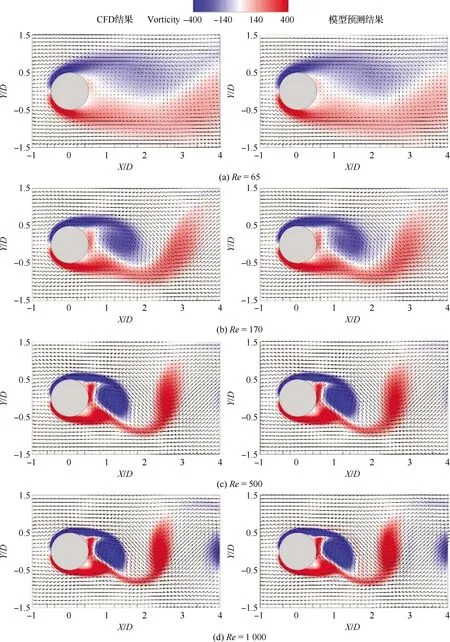
图4 不同雷诺数的模型预测值与CFD结果之间的瞬时流量比较[58]Fig.4 Comparisons of instantaneous flow fields between model predictions and CFD results for various Reynolds numbers[58]

泛化性能是监督学习中一直需要关注的问题，即对于在训练数据之外，模型能否在更广泛的流动条件下依旧表现良好。Zhu等[59]在训练和测试数据的泛化性能时考虑改变攻角和马赫数及内插和外插的情况，预测的涡流黏度、升阻力系数都与原始SA模型的结果非常吻合。Thuerey等[60]采用基于CNN的U-net网络对计算压力和速度分布的准确性进行了评估，所获得的最佳模型在未知机翼上的误差小于3%。进一步，在涉及变外形的泛化性能讨论预测类问题中，需要强调的是CNN另一个重要优势是由于其网络结构能够输入二维或高维数据，因此使得流场几何外形能够直接参与网络输入，而不需要经过预先参数化的处理，为学习复杂的几何外形提供了灵活性。Hui等[61]借助使用符号距离函数(Signed Distance Function，SDF)[62]来表示机翼的几何形状，结合CNN提取预测压力分布的能力。经过训练的网络可以精确捕获来自未训练机翼的冲击波，误差结果小于2%，并且比CFD仿真快3个数量级。Sekar和Khoo[63]采用CNN从机翼形状中提取几何参数并通过全连接网络预测流场，同样探索了深度学习方法对大量翼型的流场预测能力。当前基于CNN的参数化方法可以直接应用于3D通用几何体，并且随着机翼样本数量的增加，泛化性能得以提高。

3.2 流场外形优化

设计评价和优化问题一直以来都是CFD工程领域关注的焦点之一，而CFD实时模拟带来的复杂的计算量也一直是存在的问题。如果能够建立一个在输入输出之间的简化模型，即时预测流场流动情况，将会大大加速工程设计上的形状参数等的优化。

对流体在物体周围流动的评估时，考虑到基于数据驱动的深度学习方法在预测流场系数等问题上取得的成果，在外形设计上通过估算速度场成功对汽车外形进行更新[64-65]，这种参数化的方法可以对设计和启动优化进行交互，对学习流动的响应十分快速。Guo等[62]同样认为通过CNN构建的计算流体动力学模型能够用于设计早期阶段，提供以牺牲一定精度为代价的快速流动性能反馈。结果表明卷积神经网络模型比CFD求解器的速度快2～4个数量级。对于其他拓扑结构，CNN同样能够借助设计空间的网格描述使用卷积的方式寻找其特征，并对选择的目标函数进行合理的优化。Gaymann和Montomoli[66]通过深度神经网络和蒙特卡洛树搜索的算法进行了学习，使管道入口和出口之间的压力损失最小化。

Sekar等[67]提出了使用卷积神经网络形成反向设计的方法，可以有效地从压力分布获得机翼形状。具体而言，CNN能够从新的压力系数分布产生无需参数化的翼型几何形状，同时生成的翼型形状非常接近相关的翼型，对未知的测试样本也体现出了良好的泛化性能。而这种基于CNN的逆设计方法非常通用，在考虑雷诺数或迎角影响下的问题上同样值得进一步探索。Cunningham和Tucker[68]同样摒弃了设计空间参数化的概念，针对设计概念在应用环境中的性能问题，提出了一个验证神经网络(VNN)，能够仅根据设计图象预测生成模型在环境中的设计性能，同时以较高的准确率估计生成的设计在测试中的可靠性，而无参数化的思想也使得该方法更容易推广到其他通用的外形设计问题。

需要强调是目前基于CNN的无参数化方法在涉及实时机翼设计的工程任务中，更注重基于该方法的快速性以及与整体环境耦合的流程完整交互，而不过多强调结果的精度，所以被认为可以用于设计的早期阶段。目前受到网络的限制，无参数化的深度学习在反向设计上仍然存在着一定的误差，单纯依靠无参数化的深度学习很难满足一些精细化的外形设计需求。此时需要考虑将设计空间参数化并结合传统CFD求解对设计后期的外形进行最终优化调整，因此目前无参数化思想很难单独地运用在该类问题中。

虽然目前该方法不够完善，作者认为无参数化思想仍然是未来值得研究的方向之一。依照用户经验选择的形状参数始终会是多数设计优化问题中鲁棒性和可靠性的主要障碍[69]，而无参数化的方法理论上能够减少人工干预的数量，进而提高逆设计的准确性。可以认为随着深度学习的发展和计算能力的提升，无参数化的方法能够在外形设计中体现出一定的优势。

4 流场数据生成与应用

某些问题中所研究的流场是用一维特征量进行描述的，例如上文中涉及的压力系数等的预测。但存在一些情况更希望获取场的数据，这些数据如果使用一维矩阵虽然能够重排成二维或高维信息，但会损失空间位置的内在特性。因此在这种情况下，这些问题中需要考虑直接的二维或高维输出。在以U-Net为基础的生成类问题中，特征可以作为生成模型的输入；而另一类以生成对抗为思路的问题中，无论是生成网络中的反卷积操作，还是判别网络中的卷积与输出，都涉及了流场特征识别的运用。

4.1 生成与分辨率提升

4.1.1 流场分辨率提升

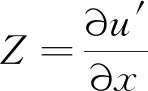
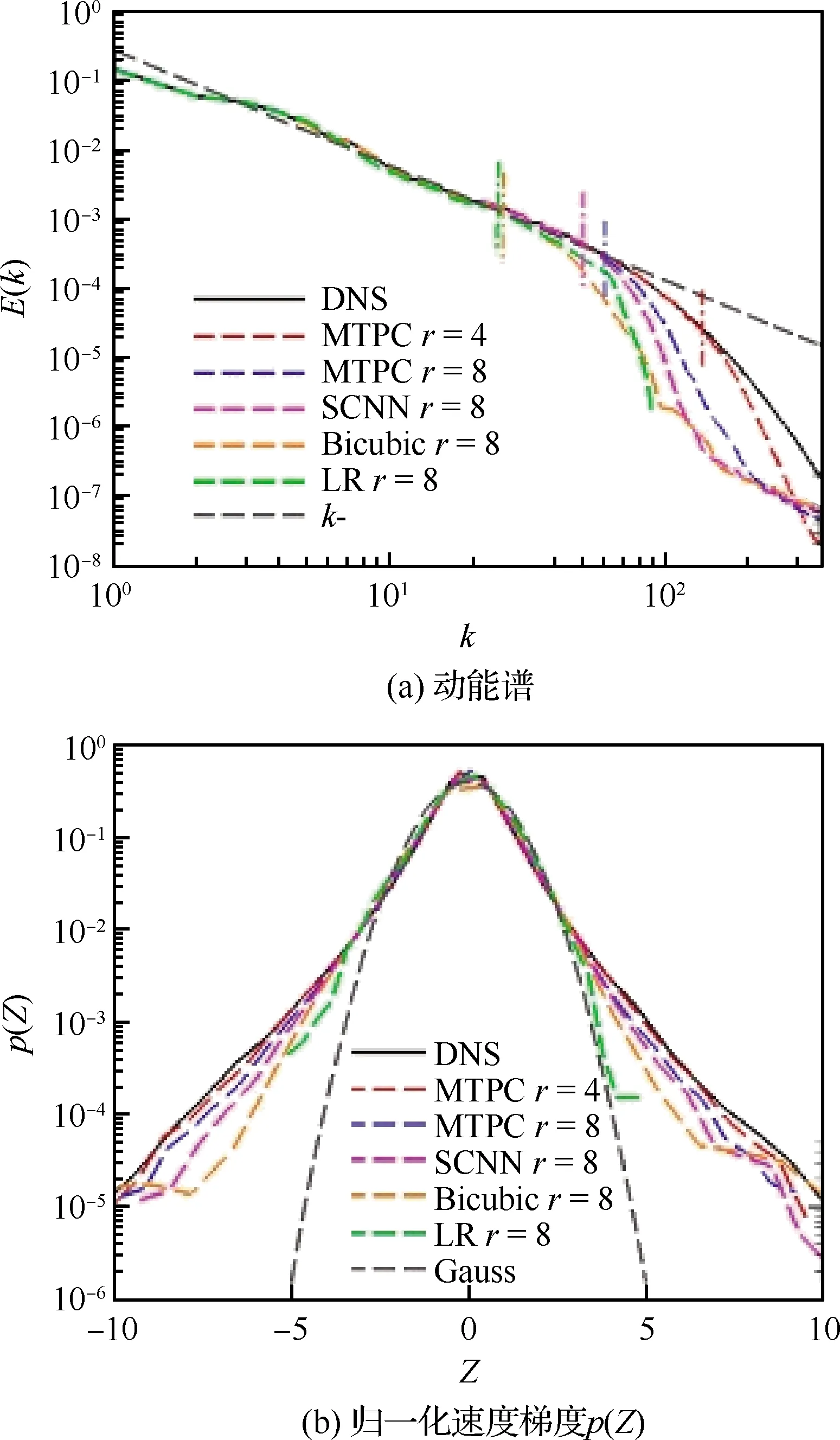
图5 动能谱和重构的各向同性湍流场和DNS数据的归一化速度梯度p(Z)的概率密度函数[70]Fig.5 Kinetic energy spectra and probability density functions of the normalized velocity gradients p(Z) of the reconstructed isotropic turbulent flow fields and corresponding DNS data [70]

除了对理论的验证探索和实验技术的精度提升，高分辨率流场的一个重要部分是对仿真模块中流场的处理。Chu和Thuerey[72]使用卷积神经网络从流体数据(如烟气密度和流速)生成特征描述子，并在学习到的描述子的帮助下提高流体模拟分辨率。Fukami等[73]中使用带有混合下采样的多尺度卷积神经网络重建高精度流场。使用二维圆柱绕流和二维均匀湍流作为测试案例，证明了标准CNN和混合模型均能够重建层流和湍流，进一步考虑通过粗糙流场作为输入重建更高精度网格规模的结构。Ferdian等构造的4DFlowNet[74]同样能够模拟实际超采样的4D流动图像。快速计算的应用十分广泛，除了医学中的流动成像问题，电影等视频领域也希望能通过流体的快速计算达到逼真的视觉效果。

4.1.2 流动快速计算和泊松方程求解

高分辨率流场生成的一个重要实现方式则是对流场的快速计算。传统CFD求解时需要从动量方程得到速度的预测项，然后代入能量方程中求解泊松方程。但令人遗憾的是，CFD中泊松方程的求解占到了整个方程组求解的绝大部分计算成本，大大制约了CFD的发展。因此希望借助深度神经网络加速泊松方程的求解。

涉及快速计算生成的应用问题主要分为两种不同的研究思路。一类主要被认为是基于数据的方法。Yang等[75]使用神经网络作为投影方程的求解器，即使在大规模数据的运算中有一定的优势，这种数据驱动的投影方法对数据的依赖性很强，泛化能力比较弱。

不同于Yang等的监督学习，Tompson等[76]探索了一种无监督的网络模型。方程的信息作为无监督的训练损失嵌入在网络中，在这样一个基于规则的框架下，能够提高整个方程的求解的长期稳定性，见图6。

图6 羽流模拟[76]Fig.6 Plume simulation[76]

上述问题都针对特定应用网格和边界条件，对适用范围有了一定的限制。Ozbay等[77]通过将原始泊松问题分解为齐次泊松问题以及4个不均匀的拉普拉斯子问题，使用新颖的方法来处理边界条件。这种方法能够在任意Dirichlet边界条件和网格参数的情况下推导Poisson方程的全卷积神经网络架构，能够以较高的精度预测泊松问题的求解。在更密集的网格时也能够捕获关键解决方案特征，提出的模型为通过机器学习加速泊松方程的求解同样提供了坚实的基础。

从偏微分方程的角度同样能够对卷积神经网络的物理特性做出说明。Long等[78-79]提出的PDE-NET中认为卷积神经网络中的卷积算子与偏微分方程中的微分算子近似，因此使用可学习的滤波器能够使得长时间动力学的预测更具有鲁棒性。同时，对施加的约束有助于确定PDE中包含的微分算子，进一步识别非线性响应函数F。

4.2 生成对抗网络

4.2.1 生成对抗网络原理

生成对抗网络(Generative Adversarial Networks，GANs)最早由Goodfellow等[80]在2014年提出，随后逐渐涌现出了许多应用，包括人脸生成[81]、图片风格迁移[82]、图像超分辨率[83]等。

生成对抗网络是由生成模型和对抗模型所组成的，生成器是输入的随机简单分布xfake=G(z)，而判别器的作用是判断自身的输入样本是真实的还是由生成器生成的假样本,D(G(z))。优化目标函数为

Ez～Pdata(z)[lg(1-D(G(x)))]

(3)

训练过程也是两个网络博弈的过程。

4.2.2 生成对抗网络与嵌入物理信息

流体力学中也开始出现基于GANs的流场重构或预测工作。Farimani等[84]认为相较于人工神经网络模型近似本构方程的解的方法，GANs更能够直接跳过基本控制方程的ANN拟合，直接生成偏微分方程的解，从而对于任意边界条件下的温度、速度和压力场进行预测，采用的稳态热传导和不可压缩流的两种模型均在测试数据上取得了较高的精度。除了精度以外，Liu等[85]着重从时间的角度考虑，计算流体力学在现有的数据压缩问题上需要的时间太多，而引入基于生成对抗网络的压缩方法能够在压缩时间上有很大的优势。文中GANs的网络结构中，D-Net用于压缩数据而G-Net用于数据重构。Wu等[86]将CNN与GANs相结合，建立了参数化超临界翼型和跨声速流场的映射ffsGAN，能够较好地在高维流场上进行预测。

进一步，在四维物理场的问题中，生成对抗网络同样能够对流动进行处理。Xie等[87]提出的TempoGAN网络在判别器的部分进行了两方面考虑，分别对空间和时间进行了判别。这种方式能够生成更详细真实和时间一致的物理量。Lee等[88]使用GANs预测了湍流中精细分辨率下的小尺度特征。

因为涉及到生成网络和对抗网络互相博弈的问题，GANs在训练时面临许多难以收敛的情况。这种情况下，学者们在流体力学问题中也做出了相应的努力。Lee等[89]采用4个深度学习网络(是否考虑守恒定律的生成对抗网络和是否考虑守恒定律的卷积神经网络)，通过对不同流态下圆柱周围非定常流场的研究，发现4种深度学习网络在短期预测时均可预测流量，但在长期预测时，是否考虑物理损失对预测结果产生了一定的影响。如何正确的向网络中引入物理信息(例如质量和动量守恒的信息)是值得关注的问题。Wu等[90]在生成器中同时嵌入了物理约束(守恒律)和统计约束，提升后的GANs能够更好地保存高阶数据信息。同时，由于约束的存在可以减少解空间，因此带来了更低的计算成本(图7[89])。Lin等[91]从网络结构的角度对算法进行了修改，生成网络不再尽量去欺骗判别网络而是寻找对应关系的匹配问题。这种由流体输运公式的启发的新算法比典型GANs在收敛性上更好。

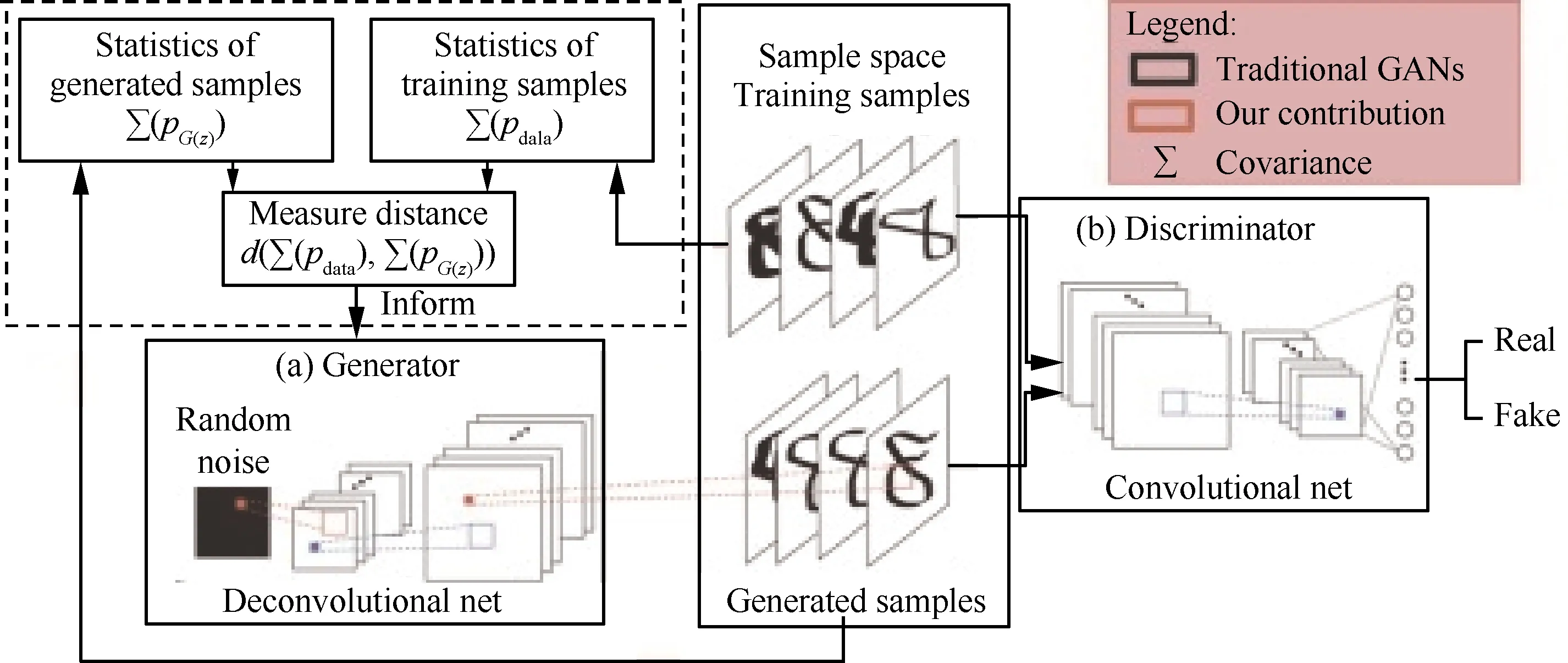
图7 嵌入统计数据的生成对抗网络[89]Fig.7 Architecture of statistics-informed generative adversarial networks[89]

5 结论与展望

本文主要介绍了卷积神经网络在流场特征类问题的应用。卷积层能够很好地对流场特征进行处理，同时结合不同的网络结构应对不同类型的问题。围绕这一研究热点，概述和归纳了这一研究领域的进展与成果。

1) 流场降阶模型(ROM)。除了和传统降阶方法结合，卷积神经网络同样能够进行降阶数据处理。基于深度神经网络的模型可以得出流场不同状态的特征，加速了流场计算效率。除此之外，ROM还可以增强物理认知，卷积分解出的特征能够类比POD及其他模态分解方法，得到的主导模态可以表示出流场的流动行为。

2) 与流场关心量相联系的问题处理上，降阶后的特征通过网络与关心量相连，能够构建输入输出之间的简化映射，达到对流场所关心量进行预测的目的。此外，基于卷积神经网络的模型能够加速流场中外形优化设计的工作，以较少的计算代价解决在复杂环境中的优化问题。

3) 对于流场的生成类问题，从基于自动编码器U-Net的角度和生成对抗网络的角度都能够达到精度提升的效果。其中数据驱动的监督学习能够很容易联想到泊松方程的快速求解，继而基于规则的泊松方程求解方法。和偏微分方程的关系也进行了讨论。

此外，本文还提出了几个值得讨论的问题。

首先，对于特定的物理问题，合适的算法选择非常关键。DNN适合基础映射类问题，RNN适合具有记忆性的序列问题，而CNN更能够考虑到空间位置信息，同时卷积操作也起到了特征识别的功能。对于文中的流场特征识别和特征深层次的运用的问题上，很多研究者在方法对比中也证明了CNN算法在相关算例中计算效率和精度上的优势。进一步，卷积神经网络并不是单独存在的，不同算法之间的融合也会是一个重要的考察方向。例如CNN和GANs结合的DCGANs，CNN和自动编码器形成的U-Net网络等。网络和算法的发展不是固步自封的，而是不同的网络之间互相学习互相借鉴，CNN本身也在和不同的算法结合中发展，使得能够更好地适用于流场特征识别问题中不同的研究分支。

其次，关于模型的泛化性能的问题。监督学习作为最经典的思想方法之一，从代理模型的角度在早期尝试中取得了非常好的成果。但是对于测试数据的范围有一定的要求，即监督学习的一条重要原则是希望训练数据和测试数据独立同分布。因此在提升泛化性能的考察上，一方面是从大数据角度出发，理想情况下使模型本身见过相同或在相近范围内的测试数据来源，从训练数据的广泛性上对模型进行覆盖；另一方面同时从算法的角度，考虑问题中无监督学习的参与，例如文献[76]中监督的优化目标是对预测速度场散度的L2范数，而不是普遍意义上的与真实值的差量，一定程度上解决了监督学习下泛化能力的问题。进一步，以强化学习为代表的元学习方法同样能够较好地处理与监督学习中泛化性能相关的问题，强化学习中智能体能够根据环境的反馈自适应地选取合适的动作，在流体力学的主动流动控制和外形优化类问题中都取得了很好的成果。

对于深度学习方法在流场识别领域的理解，除了上述以网络结构为主的分类方式，从数据驱动和在网络中嵌入物理的角度同样可以进行分类介绍。认为从单纯的数据驱动到嵌入物理是流体力学和深度学习结合的重要突破。单纯数据驱动方法对于一些映射类的问题是可行的，但这并不是最终的目的。原因主要有以下两个：首先希望所得到的模型能够提供一定的物理解释，而不是仅得到一个黑盒子；其次单纯数据驱动也会带来泛化性能上的一些问题，因为数据驱动的监督学习算法对训练数据的依赖非常大，而带有物理嵌入的深度学习才能打破当前数据驱动问题带来的瓶颈。近年来，深度学习作为一个蓬勃发展的领域，在不断的探索中也出现了许多有趣的算法，以CNN为代表的网络模型能够从不同的角度挖掘输入数据之间的联系。但对于物理问题而言，从图像等角度对物理问题分析固然是一种可行的方法。然而如果能直接把已知的一些物理规律加入网络，借此减少网络优化训练的负担；甚至利用物理规律直接主导目标网络生成的结果，这将是一个值得研究的问题，也会是将来流体力学等物理问题和深度学习结合的重要研究方向。