面向稀薄流非线性本构预测的机器学习方法

李廷伟，张莽，赵文文，陈伟芳，蒋励剑

1. 浙江大学 航空航天学院，杭州 310027 2.中国电子科技集团公司第五十四研究所 航天系统与应用专业部，石家庄 050081 3.中国运载火箭技术研究院 研究与发展中心，北京 100076

钱学森根据努森数Kn定义流体的稀薄程度，将流动区域划分为连续流域(Kn<0.01)、滑移流域(0.0110)，稀薄非平衡流域包含除连续流域以外的3大流域[1]。

连续流域符合流体力学连续介质假设条件，连续介质流体力学是其理论基础，其中最具有代表性的控制方程为Navier-Stokes(N-S)方程，形成了以广义牛顿定律和傅里叶热传导定律为基础的基于NSF(Navier-Stokes-Fourier)关系的连续流数值模拟计算方法，此方法的发展为其他各种方法的建立提供了宝贵经验。稀薄非平衡流域中气体稀薄属性逐渐凸显，例如物面出现了十分显著的速度滑移与温度跳跃现象。此时在物面附近的努森层内，连续介质假设已经失效，准确地说是基于3大守恒方程(质量守恒、动量守恒和能量守恒)推导出来的黏性应力项与热流项已经不能再简单使用低阶宏观物理量(速度、温度)的梯度线性表征，即线性本构关系已经不再适用于精准描述稀薄非平衡流动问题。

对稀薄非平衡流问题的研究主要围绕稀薄气体流动控制方程——Boltzmann方程开展，它是分子气体动力学的基本方程，可以不受努森数的限制对连续流到自由分子流整个流域进行统一描述。Boltzmann方程是一个复杂的七维积分/微分方程，大部分研究均是对其直接或者间接求解，发展形成了多种数值计算方法与理论，统一气体动理论格式(Unified Gas-Kinetic Scheme， UGKS)[2]是其中一种代表性方法。UGKS方法使用Boltzman方程的Bhatnagar-Gross-Krook(BGK)[2]类模型方程作为控制方程，用有限个离散速度替代整个速度空间，在一定条件下均能给出较为准确的流动特征，具备求解各流域多尺度问题的能力[3]。UGKS方法采用BGK类模型方程基于当地积分解对通量进行构造，将分子运动与碰撞过程自然地耦合在一起，物理意义更加明确，突破了DSMC方法[4]解耦处理所带来的计算时间步长小于分子的平均碰撞时间、计算单元网格尺度小于分子平均自由程的限制。但由于UGKS方法在求解过程中依赖速度分布函数对速度空间进行离散，这对计算与存储的要求非常高，多维与高速条件下计算效率较低。

随着计算机理论与技术的迅猛发展，大数据时代启发了人类思考问题新的思维，基于数据驱动和机器学习的研究方式也应运而生。研究人员开始通过机器学习的方法解决流体力学领域中难以解决的问题，目前在气动优化设计[5-9]、湍流问题[10-15]、非定常气动力建模[16-20]等领域上已经开展了很多卓有成效的研究工作。

以N-S方程和UGKS方法为理论基础，提出了一种适用于稀薄非平衡流数值模拟的基于数据驱动非线性本构关系(Data-driven Nonlinear Constitutive Relations, DNCR)的数值计算方法。基于流场特征参数采用机器学习方法对N-S方程线性的黏性应力项与热流项进行非线性离散重构，理论适用范围可以覆盖较大来流努森数条件，通过耦合非线性本构关系求解宏观守恒方程得到待预测状态稀薄非平衡流动数值解。与传统机器学习建模方法摒弃基本物理规律直接对数据进行训练与预测的思想相比，DNCR方法未抛弃物理规律而是对流体本构关系进行修正后耦合守恒方程迭代求解，同时保留了数据建模与物理建模的优点，方法物理意义更加清晰明确。

在DNCR方法中，采用的具体机器学习算法为极端随机树[21-22](Extremely Randomized Trees)算法。在机器学习算法中，针对所研究的具体问题选取低冗余、高代表性的特征参数对于机器学习算法的泛化性能和运行效率具有重要影响。本文拟通过二维顶盖驱动方腔流算例对高维非线性建模涉及的特征参数选取、参数调优开展相关验证与研究工作，选取若干典型状态对极端随机树模型的泛化性能开展研究，并评估相关模型与方法的计算精度与计算效率。

1 数据驱动非线性本构关系计算方法

DNCR基于N-S方程和UGKS方法的数值模拟计算结果作为流场样本训练数据，采用机器学习方法构建热流/应力项与流场特征参数的高维复杂非线性回归关系模型，对N-S方程本构关系进行非线性修正。通过耦合数据驱动的非线性本构关系求解宏观量守恒方程得到稀薄非平衡流数值解。

DNCR方法计算流程如图1所示，ψ代表在N-S流场数值模拟结果中提取的特征参数，作为机器学习模型的输入量，ΔΘ为标记参数，作为机器学习模型的输出量，即机器学习模型建立了ψ与ΔΘ之间的复杂高维回归关系，与非线性本构物理建模函数的区别在于其本构关系没有具体数学表达式，而是全流域存在离散当地映射ψ→ΔΘ，所形成的离散本构映射关系在全流场计算域适用。而模型泛化性能取决于训练集特征代表性与特征参数选取，理论上若特征参数选择未涉及到任何与空间网格与当地坐标值直接相关的参数且训练集包含相似的非平衡流动特征，机器学习模型就具备一定的迁移预测能力。

图1 DNCR示意图Fig.1 Schematic of DNCR

DNCR方法的一个重要特点是训练与预测过程相对独立，图1中红线与绿线分别表示了训练与预示流程。模型训练过程通过对包含不同典型流动特征的基础流场数据集开展训练，获得ψ与ΔΘ之间的复杂回归关系。而预测过程则首先采用N-S求解器对待预测状态开展初步计算，获得待预测当地特征值ψ，然后采用已训练生成的回归关系ψ→ΔΘ得到待预测流场当地标记值ΔΘ，最终通过时间推进方式求解质量、动量与能量守恒方程，耦合非线性本构关系完成计算，守恒方程为

(1)

式中：Q为守恒量；E、F为无黏通量；Ev、Fv为黏性通量。控制方程中黏性应力张量与热流项表达式为

(2)

式中：τ为黏性应力项；μ为黏性系数；T为温度；u、v为速度；κ为热传导系数；q为热流项；下标Tag表示待预测流场当地标记值。式(1)与式(2)随着时间推进，相关热流、应力张量与流场梯度量向标记值趋近，最终完成计算收敛，获得待预测流场定常解。

当物体或扰动源的速度大于扰动信息的传播时，扰动无法向上游传播所形成的强压缩间断称为激波。一维激波结构是最简单、最基本的非平衡流动现象之一，是研究本构关系与非平衡流动的典型算例，可以用来对模型进行验证[23]。

N-S、UGKS、DNCR相同网格下，采用单原子气体Ar作为模拟气体，其动力黏性系数μ采用逆幂律公式[24]计算：

(3)

单原子气体Ar物性参数取μ0=2.272×10-5Pa·s，T0=300 K，γ=1.667，Pr=0.667，R=208.16 J/(kg·K)，其中μ0为Ar在温度T0下的动力黏性系数，T0为Sutherland温度常量，γ为比热比，Pr为普朗特数，R为气体常数，逆幂律幂次取ε=0.72。计算状态如表1所示。

表1 一维Ar激波结构计算状态

图2 激波结构密度分布Fig.2 Density distributions in shock wave

图3 激波结构速度分布Fig.3 Velocity distributions in shock wave

图4 激波结构压强分布Fig.4 Pressure distributions in shock wave

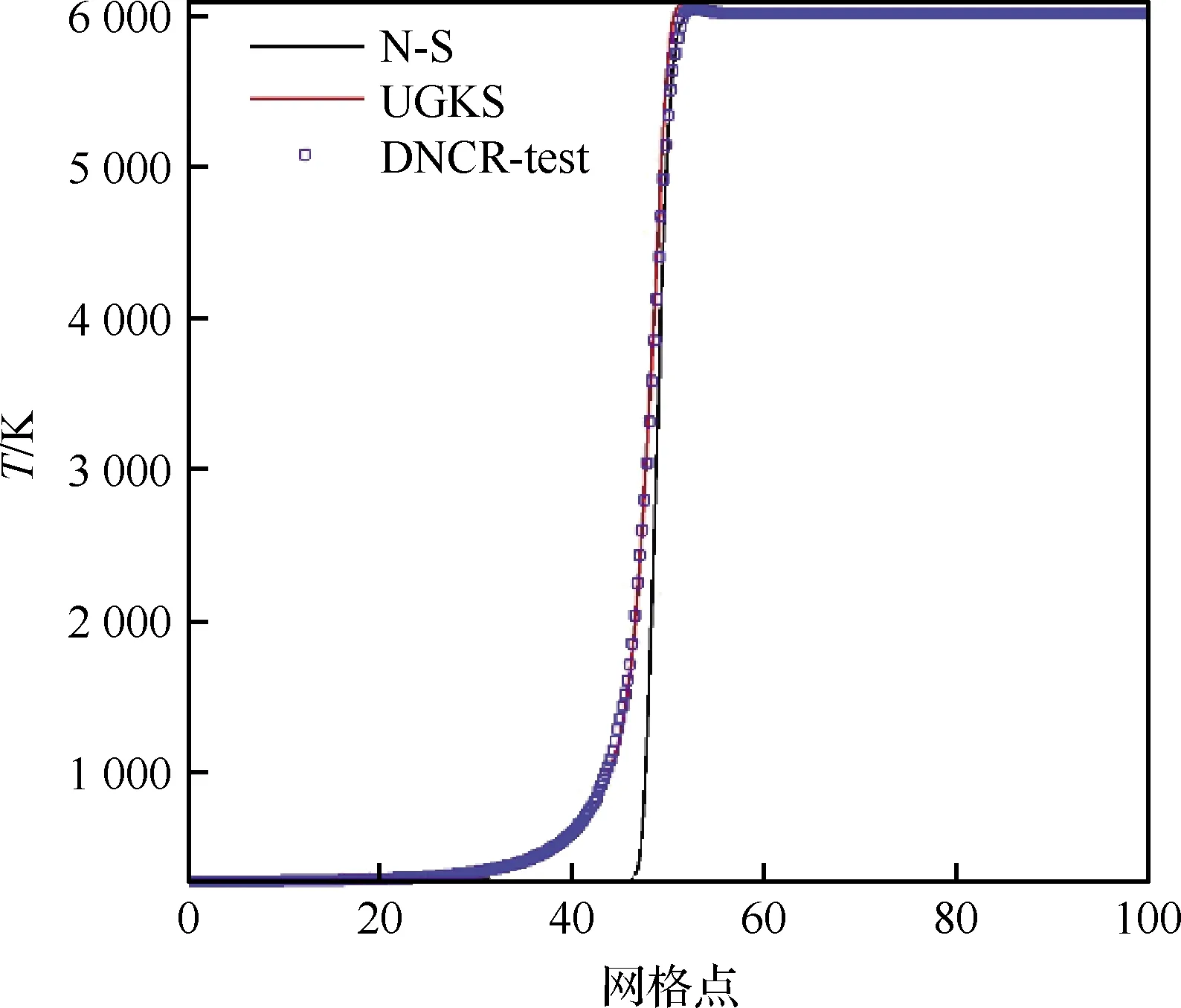
图5 激波结构温度分布Fig.5 Temperature distributions in shock wave

2 训练数据集生成

本文选取图6所示顶盖驱动方腔流动作为测试算例，计算网格如图7所示，计算网格为61×61均匀网格，速度离散为28×28。选取5组稀薄非平衡流动状态生成训练数据集，计算状态如表2所示。

图6 顶盖驱动方腔流示意图Fig.6 Schematic of lid-driven cavity flow

图7 二维顶盖驱动方腔流计算网格Fig.7 Grid of two-dimensional lid-driven cavity flow

表2 二维方腔计算状态Table 2 Calculation state of two-dimensional cavity

3 机器学习模型

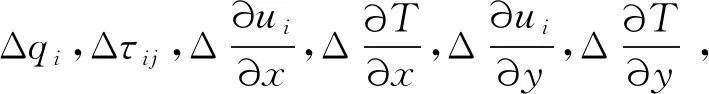
3.1 CART与极端随机树算法

X与Y分别为特征输入和标记输出变量，并且Y为连续变量，给定训练数据集：D={(x1,y1),(x2,y2),…,(xN,yN)}。

回归树是用于研究回归问题的决策树模型，决策树是一种树形结构的基本分类与回归算法。在机器学习中决策树是一个预测模型，代表的是对象属性(即特征参数)与对象值(即标记值)之间的一种映射关系。一个回归树对应着输入空间(即特征空间)的一个划分以及在划分的单元上的输出值。假设将训练数据集所在的输入空间划分为M个单元：R1,R2,…,RM，这里的单元可以理解为从最顶端往下依次划分构建的M个分支，每个分支只对应一个输出值。递归地将每个区域划分为两个子区域并决定每个子区域的输出值c，构建二叉决策树。

1) 选择最优切分变量j与切分点s：特征空间包含多个特征参数即特征变量，决策树的构建就是每层进行二叉树的划分，划分时采用某特征变量能够使误差最小，此变量即为最优切分变量；切分点指的是切分变量进行左右划分的值，小于此值划分为左子树，大于此值划分为右子树，切分时某切分点能够使误差最小即为最优切分点。通过求解:

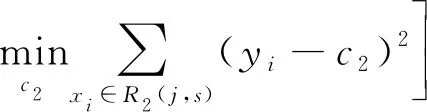
(4)

遍历变量j，对固定切分变量j扫描切分点s，选择使式(4)最小的(j,s)。

2) 用选定的(j,s)划分区域并决定相应的输出值：

R1(j,s)={x|x(j)≤s}

R2(j,s)={x|x(j)>s}

(5)

3) 继续对两个子区域调用步骤1)、2)，直至满足条件。

4) 将输入空间划分成M个区域R1,R2,…,RM，生成决策树：

(6)

极端随机树在生成CART过程中选择划分属性不再是选择最优属性而是完全随机选择。采用训练数据集进行并行训练得到t个CART，对本文回归问题模型最终采用平均法：

(7)

3.2 特征参数选择

在DNCR方法中，流场特征参数构成特征空间{ψ}，热流、应力修正所需各项构成标记空间{ΔΘ}。选取低冗余、高代表性的特征参数对机器学习算法的泛化性能和运行效率具有重要影响。首先从物理机理上考虑，选择表征流场稀薄非平衡特征的参数，例如基于当地流场梯度的局部努森数KnGLL(ρ,P,T)作为主要的流场特征参数，然后尝试加入其他参数并最终选取适当参数集作为流场特征参数建立特征空间。

本文采用方差过滤准则进行特征选择，方差越小，表示该特征的数据差异越小，可以认为这个特征对区分样本贡献不大，导致预测的效果越差，因此可以剔除此特征或降低特征权重。另外考虑到真实物理问题中不同物理量之间数据的量级可能存在较大差异，量级较大导致方差较大，为了避免这一不利因素，使用标准差与极差的商值消除量级影响进行特征选择。

(8)

式中:X={x1,x2,…,xn}代表某一特征参数;n代表样本点的数量;μ为X={x1,x2,…,xn}的算数平均值。标准差与极差做商的目的在于消除数据量纲的影响。

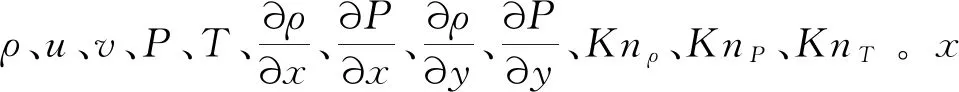
图8 特征参数标准差对比Fig.8 Comparison of standard deviation of characteristic parameters

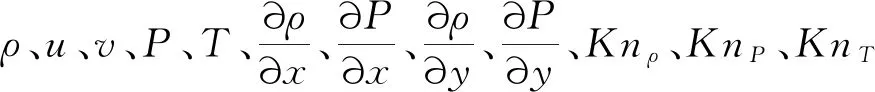
(9)

式中：Ypredict代表预测的标记值，Yactual代表真实的标记值，均可看作形如Y={y1,y2,…,yn}的向量，yi代表某网格点标记值，n代表计算网格点的数量。

图9 余弦相似度对比Fig.9 Comparison of cosine similarity

3.3 极端随机树参数调优

在研究具体问题时，不同机器学习算法中都有许多的参数需要人为设定，即使是同一种算法，面向不同回归问题的参数配置也有所区别，最终得到的模型性能表现往往也存在十分明显的差别。

对于极端随机树算法来说，主要参数包括框架参数：基学习器的数量n_estimators、度量分裂的标准criterion、是否采用袋外样本来评估模型的好坏oob_score；决策树参数：决策树的每个节点随机选择的最大特征数max_features、叶子结点上应有的最少样例数min_samples_leaf、决策树最大深度max_depth等参数。本文重点对n_estimators与max_features两个参数进行研究，其余参数均采取默认设置，研究方法为单一变量法。

本文采用可决系数[27]评价参数调节后的模型优劣情况。可决系数表示一个随机变量与多个随机变量关系的数字特征，即可决系数值越大越接近于1时说明特征参数对标记参数的解释程度越高。

(10)

采用Kn=0.7与Kn=1.3两组状态对机器学习模型进行训练，对Kn=1.0状态进行预测。选取n_estimators在[1,1 000]范围内，R2随n_estimators变化趋势如图10所示。可以看出R2最终趋近于一个比较稳定的值，拟合较好且随着基学习器的数量增加未出现严重过拟合现象。如图11所示，模型的训练时间与基学习器数目基本满足线性关系，考虑到模型训练的时间成本，本文中选取n_estimators=300。

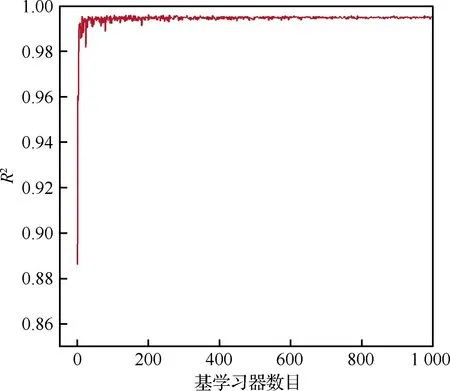
图10 R2随基学习器数目变化曲线Fig.10 R2 variation curve with n_estimators

图11 训练时间随基学习器数目变化曲线Fig.11 Train time variation curve with n_estimators

根据前文中确定使用的12个特征值，max_features在[1,12]范围中取值。为避免偶然误差，训练1 000次后取平均值，得到R2值随max_features变化趋势如图12所示。可以看出在DNCR方法中极端随机树的预测准确性随着max_features变化大致呈现递增的趋势，max_features的大小对模型训练预测时间的影响可以忽略不计，在本文中选择max_features=12。其余模型参数及其他待预测物理量的模型参数调优过程与之类似。

图12 R2随最大特征数变化曲线Fig.12 R2 variation curve with max_features

4 DNCR计算精度与极端随机树泛化性能分析

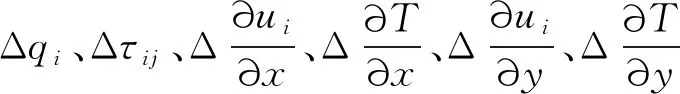
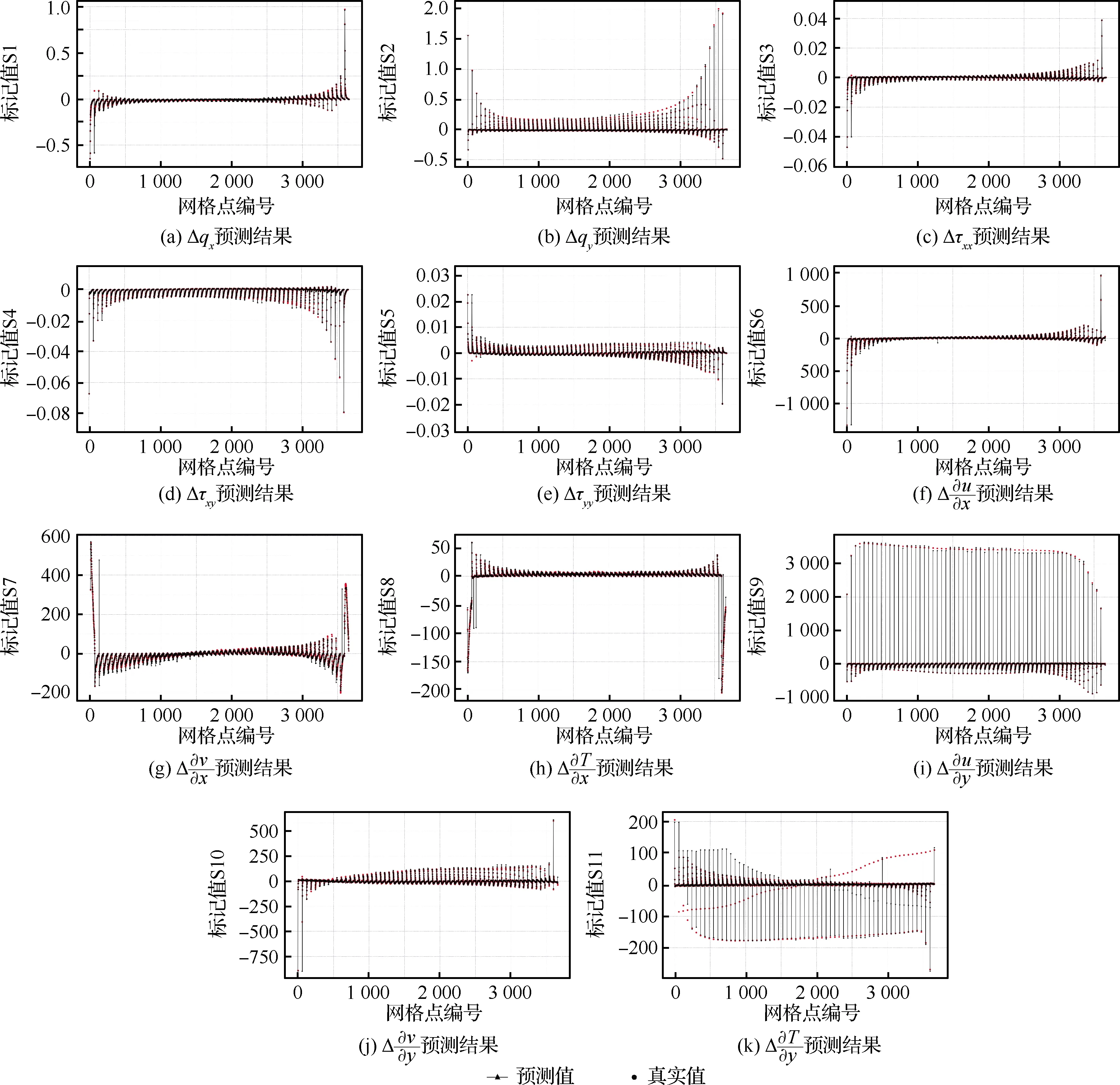
图13 预测情况Fig.13 Prediction situation

为更好地反映预测值与真实值的对比情况，采用均方误差(Mean Square Error，MSE)和均方根误差(Root Mean Square Error，RMSE)可以衡量预测值同真值之间的偏离程度。

(11)

(12)

标记值S1～S11的MSE、RMSE、R2情况如表3所示。从表中可以看出MSE与RMSE与标记值本身数据量级有关，并且与其量级相比，MSE与RMSE的值处于较低水平即预测效果较好，通过观察R2值也以很好佐证，除S11预测最差外，其余均能达到0.98以上水平。

表3 标记值误差特性Table 3 Error characteristics of predicted values

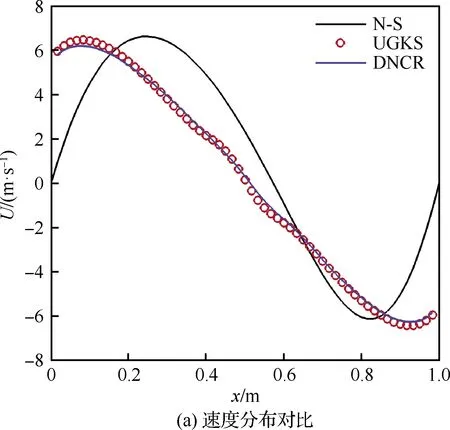
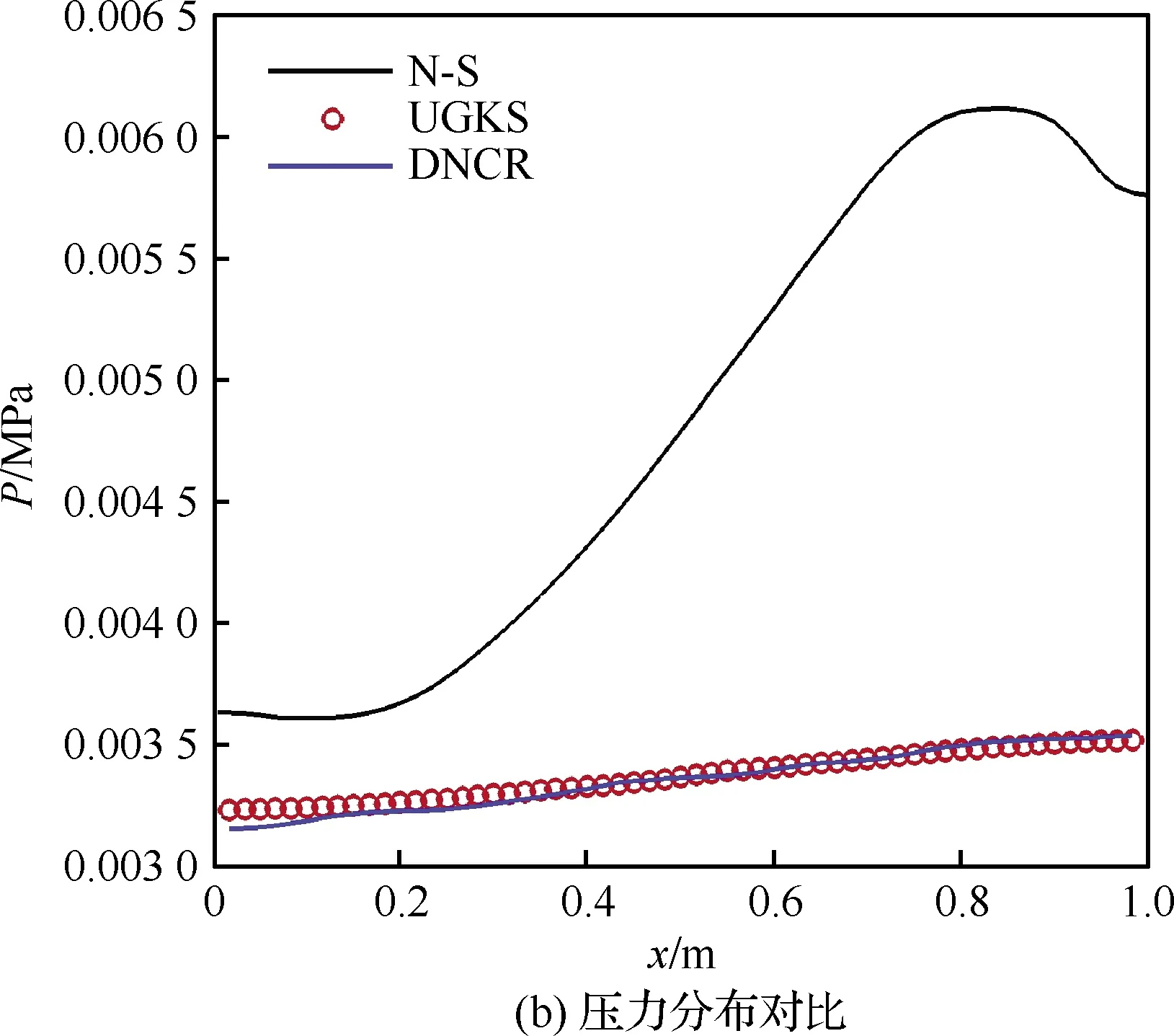
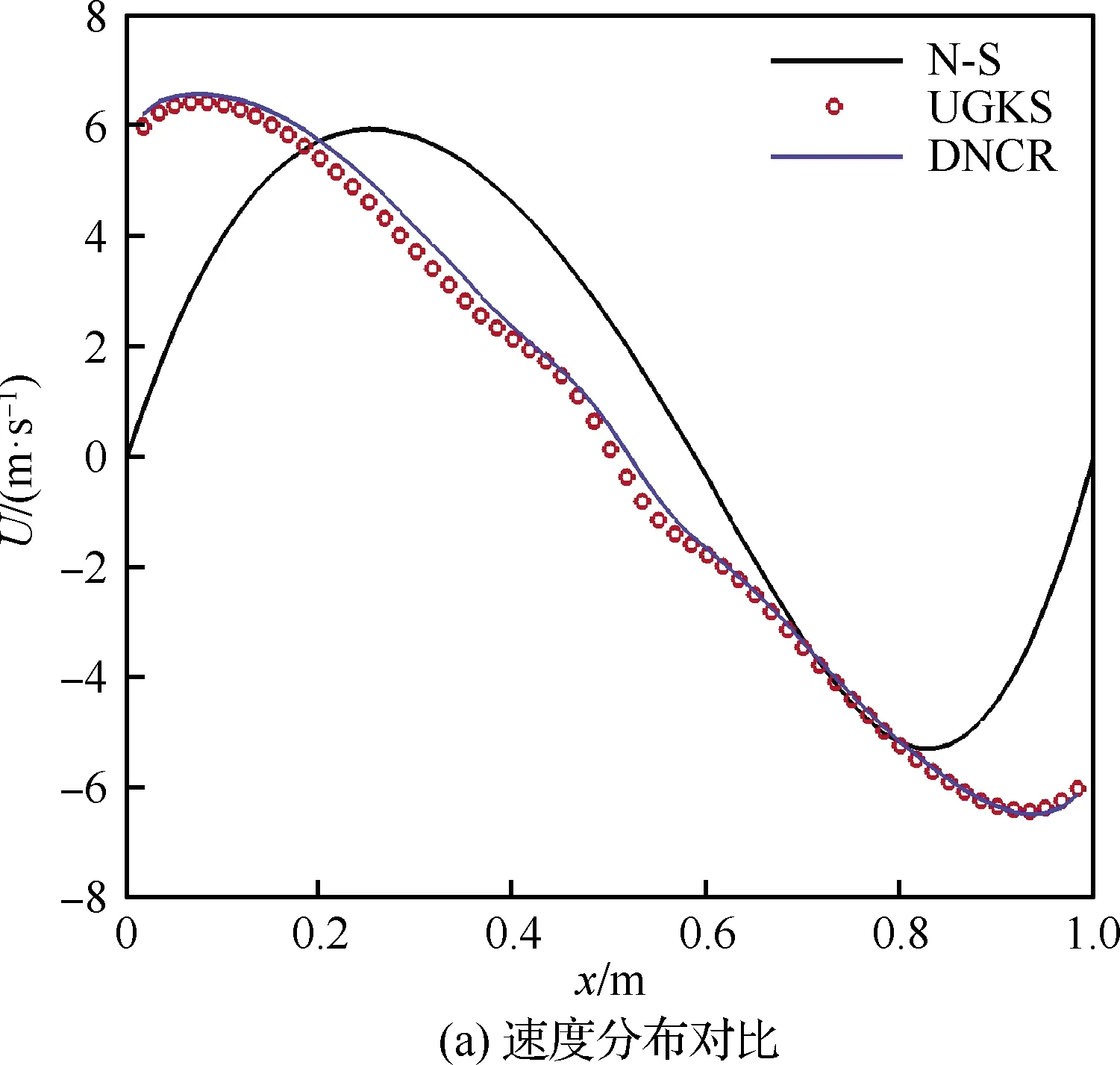
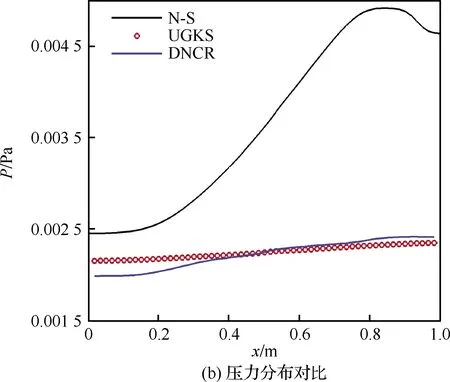
将每个网格点预测得到的标记值读入DNCR计算程序迭代求解守恒方程，最终得到收敛待预测Kn=1.0时的流场。为了直观对比计算精度，如图14所示，选择y=0.5 m截线上DNCR与NS、UGKS方法的物理量分布进行对比。

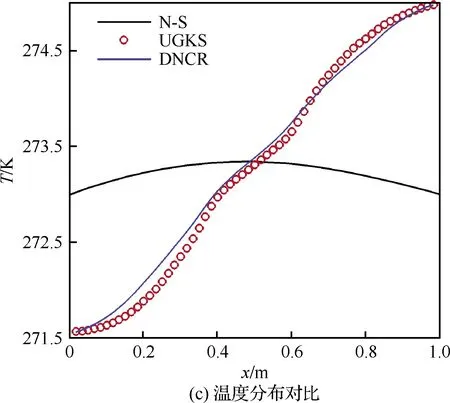
图14 Kn=1.0计算结果对比 (y=0.5 m)Fig.14 Comparison of Kn=1.0 calculation results(y=0.5 m)

采用式(13)计算评估精度提升情况：

(13)

式中：若ξ趋于1，则表明DNCR方法预测值与UGKS基本一致；若ξ趋于0，则表示DNCR预测值与N-S方程计算结果趋于一致。

通过计算得到y=0.5 m截线上U、P、T的结果，DNCR相比N-S精度提升分别为92.23%、97.77%、90.80%。

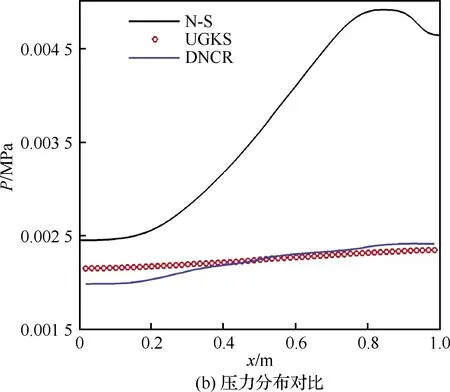
为进一步评估极端随机树的泛化能力，选取Kn=0.5与Kn=1.5两个超出训练集范围的努森数条件开展DNCR计算，重点考察DNCR方法的训练集外延数据泛化性能。其中y=0.5 m截线DNCR与N-S、UGKS方法的y方向速度、温度与压力物理量分布对比分别如图15、图16所示。DNCR较N-S方程预测精度提升情况依次为73.59%、 95.71%、71.20%和89.12%、94.36%、87.69%，精度计算公式见式(13)，可以看出在Kn=0.5与Kn=1.5条件下，DNCR较N-S方程预测精度提升百分比与Kn=1.0状态时相比略有下降，但仍保持较高水平，即DNCR方法中采用极端随机树模型具有较好的泛化性能。

图15 Kn=0.5计算结果对比 (y=0.5 m)Fig.15 Comparison of Kn=0.5 calculation results (y=0.5 m)

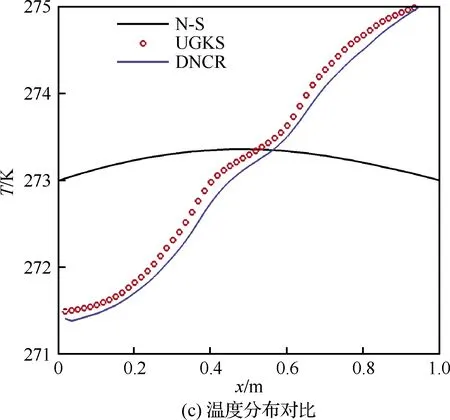
图16 Kn=1.5计算结果对比 (y=0.5 m)Fig.16 Comparison of Kn=1.5 calculation results (y=0.5 m)

计算效率方面，由于DNCR方法与N-S求解方法的区别仅在于对线性应力与热流项进行了非线性修正，因此其迭代求解速度与N-S方程基本相当。但DNCR方法需要首先采用N-S方程对待预测状态进行预计算并提取流场特征值作为机器学习模型的输入数据，最终才能在N-S计算结果上耦合数据驱动的非线性本构关系求解宏观量守恒方程得到稀薄非平衡流数值解，因此DNCR计算时间较N-S方程会有所增加，若不考虑机器学习模型训练时间，DNCR与N-S方程计算效率能够保持同一量级。

5 结论与展望

机器学习中的极端随机树模型对基于数据驱动非线性本构关系(DNCR)的复杂高维非线性回归问题具有较好的建模能力，其中特征参数的选择与模型参数的调优是机器学习建模中十分重要的关键问题，直接影响模型性能与精度。本文在DNCR方法基础上通过不同努森数条件下二维顶盖驱动方腔流算例对高维非线性建模涉及的特征参数选取、参数调优开展相关验证与研究工作，选取若干典型状态(包括训练集外延状态)对极端随机树模型的泛化性能开展研究，评估了相关模型与方法的计算精度与计算效率。计算结果初步表明通过特征参数筛选与模型调参，DNCR中的极端随机树模型不仅对训练集努森数上下限范围内中间状态具有较好的预测能力，对训练状态范围以外的外延状态预测效果也较好，体现出了一定的泛化能力。同时，DNCR方法在模型训练完成后计算效率与N-S方程基本保持同一量级，能够同时提高现有非平衡流数值方法的计算精度与计算效率，具有较高应用潜力。

然而，作为机器学习方法在物理建模过程中的应用案例，这类方法仍普遍面临以下问题：① 与已知物理定律关联困难；② 公开高可信度数据集匮乏。因此，针对现有DNCR方法在机器学习模型泛化性能、训练集数据来源与数据成本及气固边界条件物理适定性方面的研究尚存在较大空白，需要有针对性地开展相关理论与应用创新性研究，进一步提升DNCR方法非平衡流动描述能力。