AWGN信道中BPSK误码率仿真分析

丁 凯

（海军92785部队，辽宁 绥中 125208）

1 引言

在数字通信系统中，信道由于受到各种自然界和人为的干扰，会使接受的信息发生延时、丢失、错误等情况。客观存在的高斯白噪声在科学研究及工程领域有着广泛的应用，利用高斯白噪声信号源测试和检验系统的抗干扰性能即是其中一例。在基于MATLAB/Simulink仿真二进制相移键控（BPSK）调制解调过程中，在信道模块中引入加性白高斯噪声（AWEN），计算比特错误率（BER）性能，并与其理论结果进行比较，即可在比特能量信号噪声比仿真范围内利用比特错误率统计工具模块很方便地测量出系统比特错误率性能。

2 AWGN信道中BPSK扩频调制

2.1 BPSK扩频调制解调原理

基带信号常包含较多直流、低频的部分[1-2]，不适合直接在无线信道传输，需要频谱搬移，因此，基带信号需要经过载波调制将频谱搬移到适合无线信道传输的特定频带处。

在二进制数字调制过程中，当正弦载波的相位随着二进制数字基带信号离散变化时，则产生二进制BPSK信号。

BPSK的信号时域表达式为：

当发送二进制符号“0”码时（an取+1），sBPSK(t)取0相位；当发送二进制符号“1”码时（an取－1），sBPSK(t)取相位。BPSK信号通常采用相干解调，相干载波为与接收的BPSK信号同频同相[3-4]。

2.2 BPSK信号调制解调过程

在BPSK信号调制解调过程的初始阶段，随机函数产生随机十比特二进制流，如图1所示。

图1 随机二进制比特序列

采用正弦信号作为载波，信息速率2400b/s，载频4800Hz，如图2。BPSK调制信号如图3所示。

图2 载波信号

图3 BPSK调制信号

实际信道中存在着各种干扰，会对通信系统造成影响。在加性高斯白噪声信道中，信道的输入信号将与信号内的高斯白噪声相叠加，导致如图4所示的波形。

图4 BPSK叠加高斯白噪声

信号接收机接收到经过调制和叠加了高斯白噪声的信号后，进行滤波和解调，并与载波相乘进行相干解调，其波形如图5所示。

图5 调制信号与载波相乘进行相干解调

在接收端，信号相干解调后通过一个低通滤波器，波形如图6所示。

图6 解调信号经过低通滤波器

抽样判决根据调制时的“0”、“π”相位来确定，由于载波恢复中相位的模糊性，假如参考相位发生变化，将导致解调过程中出现“倒”现象，恢复出的数字信号“0”和“1”呈现倒置，如图7所示。

图7 抽样判决后的信号

在实际通信系统中，由于受所处环境、仪器精密度、电磁干扰等的影响，导致了调制解调存在一定的误差，此误差即被称为误码率。

2.3 BPSK调制BER的理论性能

为研究AWGN信道中BPSK调制BER的理论性能，使用如下等效低通信号：设接收信号为r(t)，发送信号为ui(t)，比特能量为Eb，加性高斯白噪声的平均值为零，功率谱密度为N0。则AWGN信道中接收信号可表示为：

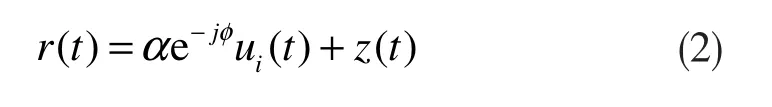
式中，0≤t≤T,i=1，2，α为一个常数，T是符号持续时间，φ是载波相位，则有传输比特错误概率：

式中，ρr是信号互相关值的实部，。

对于双极性信号，互相关系数实部ρr=-1。为便于表示，令常数α=1，则得到AWGN信道中双极性BPSK信号的BER为：

按如上方法，在给定信噪比值的条件下得到一系列理论及仿真数据，仿真时长为100000s，其对比情况如表1。对于不同比特信噪比下的BER理论值与仿真值的对比曲线如图8所示。

表1 10000个发送符号下的仿真及理论误码率

图8 BER理论值与仿真值对比

3 AWGN信道BPSK调制仿真模型

3.1 模型建立

为说明计算通信系统传输比特错误率（BER）整个过程，建立如图9所示的BPSK仿真模型[5]。

图9 BPSK调制仿真模型

在BPSK调制与解调模块中增加AWGN模块，AWGN信道中设置Mode参数，仿真结果如图10所示。当Eb/N0设置为100dB、信噪比取值很大时[6]，AWGN模块不会引入传输错误，如图10(a)所示，输入发送信号序列和接收解调输出的信号序列都是由一连串收发相互一致的双精度随机整数值（1或0）组成。把Eb/N0的值修改为-10 dB后[7]，产生了不少错误，收发数据序列波形变得不一致，如图10(b)所示。

图10 BPSK输入输出波形仿真结果

3.2 AWGN信道中BER性能分析

加入了AWGN信道和高斯噪声发生器模块的整体仿真模型如图11所示。在适当条件下，使用了AWGN信道的方法，与高斯噪声模块配以加法器（adder）模块的方法，两者仿真结果应该相同。此处，高斯噪声模块必须是零均值的，噪声方差应随所需要的值的变化而变化。对于复高斯噪声发生器的实部和虚部，其随机数种子应设置为不同的素数，才能保证实部和虚部这两个正交噪声分量具有统计独立性。图中的“运行方差计算模块（Running VAR）[8]”是用来计算信号功率的，并将相应信号功率的仿真值显示出来。在此也添加了误码率计算模块（Error Rate Calculation），当γb=3dB时，这两种方法的传输BER性能仿真结果分别为0.2287和0.2266，都非常接近于表1中的BER的理论值0.229，从结果上看来较为理想。

图11 整体仿真模型

4 结束语

利用数字信号载波传输系统中存在的信道噪声误码，借助于AWGN信道模块和高斯噪声器模块，在适当参数下得出了相同的仿真结果。随着仿真时间增加，统计样本随之增加，将使得误码率仿真结果更加接近理论分析值。基于蒙特卡罗统计方法得到的仿真结果与理论计算之间具有较好的一致性，而在实际工程中，要获得通信系统的理论性能往往比较困难，因此，仿真手段几乎成为通信系统性能评估的最佳选择。