基于参数可调均值迁移滤波实现筒子纱的识别检测

李靖宇， 沈丹峰， 王 玉， 李耀杰

(西安工程大学 机电工程学院， 陕西 西安 710600)

纺织生产中多道工序都存在筒子纱的使用，比如络筒、整经和织布。采用机械手+AGV模式的自动运纱车进行筒子纱的上下机和搬运，能够降低劳动用工。课题组以无梭织机车间纬纱筒子的自动更换为背景，研究纬纱架上的纱筒采用机械手更换的方向。满筒纱从运输车辆装载到纬纱架或空筒纱管从纬纱架卸载到运输车辆是筒子纱搬运的2个过程。筒子纱的自动搬运涉及到的关键技术是筒子纱的视觉检测。图像纱筒的边缘信息是纱筒的基本特征，通过边缘信息的提取，可以判别纱筒的大小与朝向，从而驱动机械手完成纱筒抓取工作。图像边缘保留滤波算法主要有高斯双边滤波和均值迁移滤波，该方法本质上是一种基于非参数概率密度梯度估计的迭代算法，在统计的特征空间内实现了边缘细节的平滑。

课题组采用改进的均值迁移滤波方法完成筒子纱边缘信息检测。对于均值迁移(mean-shift, MS)滤波算法，林俊杰等[1]将ANBF算法嵌入到了均值迁移算法中，提高了MS算法去除噪点的效率。张文忠等[2]在均值迁移的框架下结合卡尔曼滤波器，即使目标物被遮挡，仍可以稳定地识别追踪。温宗周等[3]提出了一种改进粒子滤波与均值迁移特征融合的目标追踪算法，在目标移动过程中受到光照或相似颜色的影响时，跟踪的效果最佳。张晓磊等[4]基于均值漂移与空间信息的导向引入目标函数，改善对图像去噪能力的鲁棒性，提高了分割精度。宋骊平等[5]提出了一种基于均值漂移和双层结构模型为群目标的假设密度滤波算法，解决了群目标合并、交叉或分裂前后数目存在的漏估现象。王文胜等[6]设计了一种分块加权模板改进频率的检测算法，提高了纱笼杆的自动化的检测效率。金守峰等[7]将对抗式神经网络将筒子纱的数据扩充，采用训练多次的神经网络定位筒子纱，可以实现多个筒子纱的抓取工作。张新建等[8]设计了基于机器视觉的筒子纱密度检测系统。郑军等[9]开发了分布式筒子纱自动收集与输送系统。刘秀平等[10]和范狄等[11]针对不同位姿的工件，提出了面向装配机器人的识别和定位方法。Huang等[12]针对遥感高光谱图像，采用自适应均值迁移算法对图像进行区域分割和滤波，每个样本点在基于图像空间位置邻域的异质性自适应估计。Zhang等[13]提出了迭代滚动引导滤波器，在保持高对比度边缘的同时，选择性的过滤小尺度细节。Elad等[14]提出整合RGF和SIR的思路，并称之为交替引导滤波，能够有效地消除小尺度细节，并保留图像中的重要边界。He等[15]系统地给出了引导滤波的定义、快速实现方法和多种应用案例，与之前各种滤波器相比，引导滤波建立在离散信号的局部线性假设之上，滤波结果综合了引导图像和输入图像的结构特点。

本研究针对的是纺织厂中的筒子纱识别，由于受到环境和纱线纹理等影响导致图像易产生噪声，因此传统的方法对筒子纱的识别效果并不理想。课题组通过基于均值迁移滤波算法与边缘检测方法的结合，使得图像降噪同时保留筒子纱的轮廓，并且得到筒子纱的外接轮廓与质心，利用横纵比的计算可对筒子纱的放置状态做出判断。课题组提出的组合方法虽在复杂多变的场合尚有一定的局限性，但在常见的环境中对于目标的识别检测具有良好的效果。

1 图像采集

筒子纱的图像采集系统，包括CMOS工业相机、LED光源、待测的筒子纱和PC机。其中工业相机的型号为MER-500-14GM，机械尺寸为29 mm×29 mm×29 mm，分辨率为(2 592×1 944) ppi，帧率为14帧/s，像素尺寸为2.2 μm×2.2 μm，镜头接口为C口，触发模式为软件触发，同时兼容opencv调用相机。相机和LED光源安装在手眼一体抓纱机械手的上端，随着机械手一起移动。抓纱机械手安装在筒子纱运输车辆上，在采集筒子纱的图像信息时，采用单目成像。图像质量主要由抓纱机械手和纱筒两者的相对关系来决定。根据两者不同的相互位置和运动情况，可构成不同的成像结果，图像采集系统如图1所示。

图1 图像采集系统示意图Figure 1 Schematic diagram of image collection system

2 图像处理

课题组针对单一目标筒子纱的识别检测流程如图2所示。

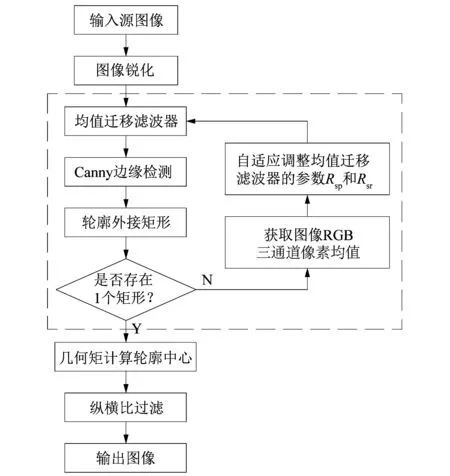
图2 筒子纱的识别检测流程图Figure 2 Flow chart of cheese identification and detection

首先对输入的源图像进行锐化处理，增强筒子纱的边缘细节，接着均值迁移滤波器实现去噪，Canny边缘检测检验去噪效果和边缘等信息是否丢失，再通过目标的外接矩形找出筒子纱；这时若图像仅存在1个矩形且为筒子纱轮廓的最小外接矩形，则继续几何矩计算轮廓中心和横纵比过滤，找到筒子纱的质心并判断筒子纱的摆放姿态。若存在多个矩形或不是筒子纱轮廓的最小外接矩形，则要修改均值迁移滤波器pyrMeanShiftFiltering中的参数Rsp(色彩域半径)和Rsr(空间域半径)，直至得到单一且准确的目标。

2.1 图像锐化

图像锐化是利用扩大高频分量来降低图像的模糊程度，加强图像轮廓和边缘细节信息。灰度反差越明显，越易于后期对目标的识别检测。图像锐化的本质是原图权重像素与拉普拉斯滤波相结合输出效果。拉普拉斯算子是二次线性微分算子，具有旋转不变性，能够满足在不同方向图像边缘的锐化要求，其获得的边界比较细，包含较多的细节信息。图像锐化的Laplacian公式为：

(1)

式中：i,j分别为图像中的像素点。

由式(1)可以看出，Laplacian算子是4倍中心元素值与其邻域值和之差的绝对值，常用的3种Laplacian算子模板：

在图像的预处理阶段，为了提升锐化的效果，同样可以脱离线性微分计算的规则，在原有的算子基础上修改模板系数，得到适合的Laplacian变形算子。

2.2 参数可调的均值迁移滤波算法

对于一定数量的像素点样本，任选其中一个样本，以该样本为中心点划定一个圆形区域，求取圆形区域中样本密度最大处的点，即像素点的质心。再以该质心点为中心执行迭代过程，直到最终收敛。在图像开窗操作的时候，同时筛选在空间范围分布的像素点，符合阈值要求的像素点参与迭代计算，基于不断更新的均值位置迁移直到不再变化，且设置特定的迁移次数作为停止条件，最终的RGB均值将赋值给中心位置。如图3(a)到3(b)，圆心迁移至样本区域的质心，此过程完成了一次迭代运算，获得了新的中心位置；图3(c)到3(d)，完成了整个迭代过程，此时找的中心位置到达最终位置，即该图像中密度最大处的点。

图3 空间域像素点均值迁移的迭代过程Figure 3 Iterative process of pixel mean migration in spatial domain

参数可调的均值迁移滤波算法的执行过程:

1) 在原图像上任取一点A0为圆心，构建色彩域半径为Rsr和空间域半径为Rsp的球形空间，色彩域和空间域的参数分别为RGB三通道和x,y坐标取值，其中空间域的范围是图像的分辨率大小，色彩域的范围是在0～255。

2) 在1)中构建的迭代空间中，计算筛选后的像素点相对于中心点的色彩向量之和，迭代空间的中心点移动到该向量的终点，并再次计算所有新样本点的向量之和，如此迭代，在最后一个样本空间内求得向量和的终点即该空间球体的中心点An，迭代结束。

3) 不断更新图像上初始中心点A0的色彩值为本轮迭代的终点An的色彩值，迭代过程形成了一个点的色彩均值漂移。对于输入图像上其他像素点，重复执行1)、2)步骤覆盖所有点位后，均值迁移色彩滤波完成。

4) Canny边缘检测计算图像梯度并求出图像边缘的幅值与方向，再利用图像边缘的细化和双阈值边缘处理，输出二值化图像。

5) 通过轮廓外接矩形标记筒子纱，如果形成单一矩形则滤波算法完成；否则，修改参数Rsp和Rsr，返回1)。

在这个过程中，Rsp和Rsr参数值影响纱筒数目的准确性。由于这种方法是基于非参数概率密度梯度估计，并没有一个设置准则。为了获得合适的Rsp和Rsr参数值，以达到准确检测纱筒数目的目的。通过多次实验，对不同灰度图像手动调整Rsp和Rsr，发现最佳的Rsp和Rsr参数与整幅图像RGB三通道灰度均值之和的均值MRGB(Mean RGB)相关，选取MRGB为[50,200]对应参数的效果图，通过MRGB与参数的对比做出实验统计结果如表1所示。

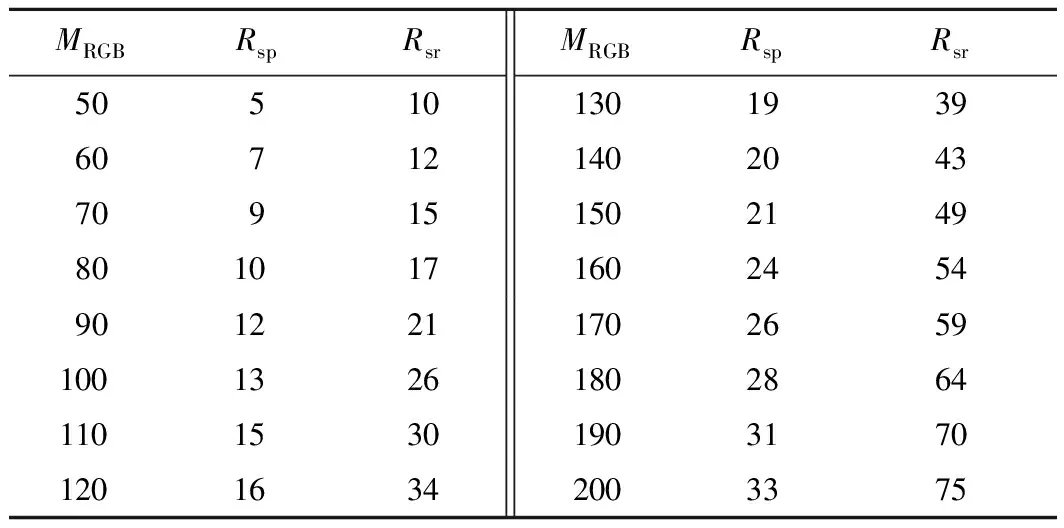
表1 不同MRGB对比下Rsp和Rsr参数的参考值

通过最小二乘法将表1的数据拟合成曲线，并推导出MRGB与Rsp和Rsr参数的拟合曲线函数。

图4中MRGB与Rsp参数的拟合曲线近似为一条直线，即拟合曲线函数为

yp=0.2xm-4.5。

(2)

同样图5推出MRGB与Rsr参数的关系式为

(3)

式中xm为横坐标。

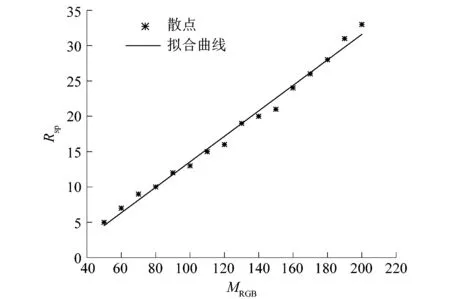
图4 MRGB与Rsp参数值拟合曲线Figure 4 Fitting curve of MRGB and Rsp parameter values

图5 MRGB与Rsr参数值拟合曲线Figure 5 Fitting curve of MRGB and Rsr parameter value

运用表1所列出的数据和拟合曲线函数作为参考，自适应调整Rsp与Rsr的参数值，减少流程中循环次数，提高方案的执行效率。

2.3 几何矩计算中心位置与横纵比过滤

几何矩可以计算筒子纱的中心位置。图像所计算出的矩集表示的是图像信息的总体特征，同样包含大量图像形状的几何特征信息，例如尺寸、方向和位置等。图像中的几何矩集包括中心矩、归一化矩和空间矩。几何矩具有良好的尺度和方位不变性，零阶矩和一阶矩计算图像中某个目标的重心，二阶矩则是计算目标的方向。对于二值化图像的边缘细节等信息，通过计算图像的几何矩与中心位置可以算出图像的中心矩和Hu矩。OpenCV中利用API函数moments便可一次得出中心矩、归一化矩和空间矩3种矩。

ic=R10/R00;jc=R01/R00。

(4)

式中：R00是零阶矩；R10,R01是一阶矩；ic和jc是图像的重心坐标，i+j=n称为n阶矩。

当外部有噪声干扰时，该方法的优点是对噪声不敏感，计算出的质心不会有太大的偏离。

筒子纱形状方向为:

(5)

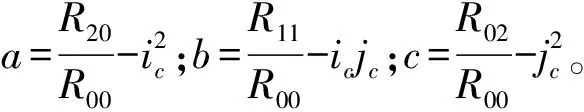
通过外接轮廓的计算得到最小与最大外接轮廓的宽和高，由此可以判断筒子纱的放置状态，横纵比过滤的公式为

(6)

式中：w为外接轮廓的宽；h为外接轮廓的高。

当rratio>0.9时，图像识别的形状近似为圆形，筒子纱的姿态为竖直放置；当rratio<0.5时，图像识别的形状近似为矩形，即筒子纱的姿态即为水平放置。

3 实验结果与分析

实验中算法运行环境为Windows 10和8 GB RAM内存的PC机，使用intel(R) Core(TM)i7-8750H CPU@2.20HZ的处理器，在VS2015平台上选用Opencv开源图像处理数据库进行实验。实验分为2部分：①对单一目标的筒子纱进行识别，按照流程图中步骤得出实验结果，同时将结果对比其他算法；②对多个纱筒进行识别，不同数量的目标对应不同数量的外接矩形，并做多组实验，得出实验的准确率。

3.1 单一筒子纱为目标的结果分析

首先是对于单一的筒子纱的识别，以实际纺织厂中的筒子纱为研究对象，结果如图6所示。图6(a)为工业相机拍到的筒子纱，经过图像锐化处理得到图6(b)，图6(c)为Canny边缘检测的结果，可以清楚的看到图像中的噪声。图6(d)～6(f)为改进算法结果，图6(g)～6(k)为均值滤波算法结果，2种方法均基于图像的锐化处理。

图6 单一目标筒子纱的识别结果Figure 6 Recognition result of single target cheese

从图6可看出：图6(e)中外接矩形数目只有一个，黑色的点为外接轮廓的质心；图6(f)的Canny边缘检测中消除了噪声，筒子纱的边缘细节保留完整。图6(h)与图6(i)中的噪声明显产生了多个矩形，并且边缘部分存在缺失。对比可以得出，课题组提出的均值迁移滤波算法具有良好的去噪和边缘保留效果，得到的外接轮廓确定中心位置，且准确地完成了筒子纱的识别检测。

3.2 多个纱筒为目标的结果分析

均值迁移滤波算法同样可以实现对于多目标的识别。以纱筒为研究对象，设置需要识别的外接矩形数目，其他采用与单一目标相同的流程步骤，结果如图7所示。

图7 多目标纱筒的识别结果Figure 7 Recognition result of multi-target yarn cheese

图7(a)是将相机拍摄角度位于垂直放置纱筒的一侧，经过一系列流程算法的处理，得到图7(d)。根据横纵比的过滤，可以看出不同放置状态的纱筒被准确地识别，同时运用不同颜色的外接轮廓矩形，其中浅色表示水平放置，深色为垂直放置，由此可以判断纱筒的放置状态。对于多目标的识别检测，图7(e)的Canny的边缘检测结果显示去噪效果良好且边缘没有缺失。

为了验证改进算法的识别效率，选取20个纱筒为检测样本进行10组实验，并且保证纱筒水平与垂直状态随机摆放，实验结果如表2所示。检测目标矩形准确率公式为：

检测准确率

该实验选取的图像背景为纱筒运输车镀锌底盘和织布车间的水磨石地面。这2种背景颜色与纱筒纹理较为接近，从10组实验的准确率数据可以得出改进算法在复杂多变的环境中对多个目标的识别仍存在一定的误差。10组实验的平均准确率达到了93.8%，证明改进算法仍具有较高的识别效率，可以满足多数情况下对筒子纱或纱筒的识别检测。

4 结语

为了满足对筒子纱的精确识别检测，课题组提出了一套基于参数可调的均值迁移滤波算法的流程设计。

1) 通过获取图像的MRGB，自适应修改均值迁移滤波算法的Rsp与Rsr参数值，提高了方案的执行效率，确保图像中筒子纱识别检测的鲁棒性。

2) 采用几何矩计算外接轮廓的中心位置与横纵比的过滤可以实现质心定位和放置状态的判别。

3) 改进算法在复杂背景下的多纱筒识别准确率达到了93.8%，表明课题组提出的方案具有较高的准确性。在接下来的工作中，可以结合相机标定得到筒子纱的质心坐标，利用机械手实现筒子纱的抓取工作。