筒子纱包装自动配重方法研究

彭来湖，祝孝裕，张少民，胡旭东

(1. 浙江理工大学 浙江省现代纺织装备技术重点实验室，浙江 杭州 310018； 2. 海宁纺织机械有限公司，浙江 海宁 314400)

国内外纺纱企业生产的最终产品是纱线，无论何种颜色的纱线以及何种生产方式，其大都以筒子纱的形式出售[1]。筒子纱是纺织行业络筒工序的产出品，是从上道工序的细纱机或捻线机上落下来的管纱，根据机织或针织等后道工序的用纱要求，使纱线长度接长并清除纱线上疵点和杂质，在络筒机上通过急行往复的导纱钩或槽筒重新卷绕成无边或有边的、具有一定形状(如圆锥形)、一定卷绕密度、较大体积的筒子纱[2]。筒子纱用来生产布匹、针织品或毛巾等相关产品，一般为圆锥形，其直径大约在120～260 mm之间，大端与小端的直径差在10 mm以内，纱线高度比管筒略低，高度在150～180 mm之间[3]。

目前，筒子纱的收集、套袋、配重、打包等包装过程大都由人工进行，工作量大，长期重复劳动易产生疲劳，且效率低下。在企业用工急缺的情况下，筒子纱的包装成为了亟待解决的问题[4]。国外的诺茵豪斯(Neuenhauser)公司推出了筒子纱的自动化包装系统[5]，可以按筒子纱的品种进行分拣、打包。但其占地面积大，而且包装筒子纱需要大量的托盘，最重要的是没有进行筒子纱的配重。国内的企业和科研单位也进行了筒子纱包装系统的研究，其中珲业公司生产的筒子纱包装系统自动化程度不高，实际没有提高生产效率。青岛环球集团生产的筒子纱包装系统直接与络筒机连接，采用悬挂式的运送方式，成本较高，并且缺少配重环节。山东康平纳公司研发的筒子纱包装系统可以对筒子纱进行大小头检测并翻转，但缺少筒子纱的配重环节。很多学者也对筒子纱的包装系统做了相关的研究，其中谢楠等[6]设计了分布式筒子纱包装与码垛控制系统，该系统拥有自动取纱、输送、包装和码垛装置，但也缺少筒子纱配重装置。杨伟[7]对筒子纱自动输送系统进行了研究，可以对多个品种的筒子纱进行分拣、输送，进行大小头翻转等，不足的是同样缺少配重环节。李瑞琴等[4]在软件上实现了筒子纱的自动包装，并没有做出实际产品，最重要的是没有对筒子纱进行配重处理。

这些纺纱企业研发半自动化包装生产线，以实现对筒子纱的自动收集、套袋、打包，减少了用工，也提高了筒子纱包装的效率，但其中缺少最重要的配重环节。由于国内大部分纺纱企业采用国产络筒机，络出来的筒子纱其品质参差不齐，直径不均匀，质量相差较大，因此，目前市场上已有的机械化打包装置不适用于此类筒子纱的自动包装。针对以上问题，本文结合自动配重包装工艺设计了总体方案，对储纱原理及配重机制进行深入研究，设计了3种配重方案，通过仿真对比测试，采用区间分布及质量配对法高效、节时。经过大量生产实践表明，采用本文研究的自动配重方案节省了劳动力，降低了企业成本的同时增加了配重效率，减少了配重时间，增加了企业的效益。

1 总体方案设计

圆锥形筒子纱打包时，纱筒与纱筒间需要尽量减少空隙，因此相连纱筒需要正反间隔排布；包装袋内纱筒的排布规律主要是三乘四，每袋质量误差控制在60 g以内。根据以上要求，设计筒子纱自动包装流水线主要由放筒运输线、动态称重分管道输送线、储纱立体库、配重组合线、翻筒包装线组成。针对各条生产线的控制需求，本文提出了一种筒子纱自动配重包装的包装流水线控制系统设计方案，软、硬件采用模块化的结构以适应筒子纱自动配重包装的需求[7]。图1示出了筒子纱自动配重包装系统方案的总体原理图。

图1 筒子纱自动配重包装系统结构原理图Fig.1 Structural schematic diagram of automatic cheese weight packing system

该系统的最大特点是通过自动配重算法实现筒子纱的称量、配重、套塑料薄膜、打包一体化。如图2所示，动态秤获得运动过程中筒子纱的质量信号，传输给主机实际筒子纱的质量，再根据当前是起始储纱模式还是实际配重模式的相应算法进行筒子纱的存储或配重。若是实际配重模式则执行后续的套袋、选择性翻转、打包等工作。起始储纱模式是开机时判断立体库中存储的筒子纱个数是否满足实际规定的个数，在不满足的情况下才进行筒子纱存储。储纱准备就绪时，则正式开始筒子纱的配重打包工作。当筒子纱满足单个筒子纱质量范围，则进行配重，通过算法判断该筒子纱是否满足实际配重需求：若满足则进行后续的套袋、打包工作；若不满足则再进行判断是否能和立体库中的筒子纱经过比较置换出满足要求的筒子纱，若能寻找到合适的筒子纱，则置换出的筒子纱也进行后续的套袋、打包工作。在这个过程中所有不满足的筒子纱从2号生产线流出整个系统。

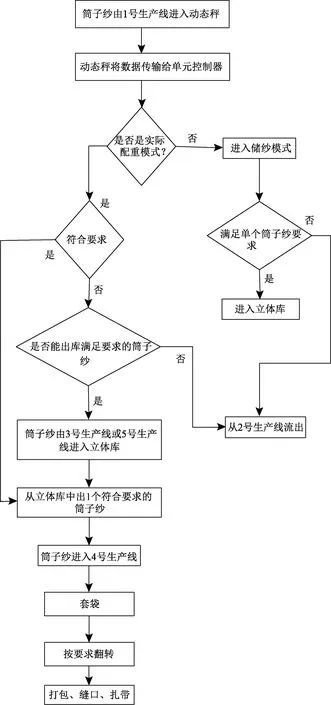
图2 筒子纱自动配重包装系统控制流程图Fig.2 Control flow chart of automatic cheese weight packing system

2 储纱模式基本原理

在起始储纱模式下，系统会读取4个立体库中已存筒子纱的个数K1，K2，K3，K4。立体库有12个储纱框架。设置储纱个数为YN(YN≤12)，K1～K4在未达到YN时，则输送的筒子纱要进入立体库中储存，直到每个立体库中的筒子纱个数都达到YN个，储纱完成，储纱模式结束。

将设置的筒子纱的质量范围平均分成轻、正常、重3个区间，在储纱时将筒子纱按照这3个区间进行储存，即一个立体库中的储纱情况要满足轻、正常、重3个区间的筒子纱数量基本均衡，以保证立体库中的筒子纱能满足后续配重模式的置换工作。

现假设筒子纱都满足设置的单个质量范围，不满足的会从2号生产线流出。若第1个筒子纱在轻区间，则先进1号立体库，再判断第2个筒子纱所在的质量区间。继续进入1号立体库，保证每个区间的个数不超过YN/3，若超过YN/3，则该筒子纱进入下一个立体库。以此类推，保证每个立体库的每个区间中在3个质量区间的筒子纱个数不超过YN/3个，这样就认为4个立体库中的筒子纱基本符合配重模式的要求。系统每次开机时都会自动检测4个立体库中的筒子纱个数，保证储纱个数达到YN。

3 配重机制分析

3.1 配重目的

纺纱企业进行筒子纱配重就是从个体具有一定质量范围的一系列筒子纱中找出给定个数筒子纱组成一包筒子纱，使其质量满足[Yw-ε,Yw+ε]，Yw为一包筒子纱的设定质量，ε为配重精度，一般固定不变为60 g。

设单个筒子纱的质量范围为[Wmin,Wmax]时，可判定为合格筒子纱，则：

根据纺纱企业的实际情况，现假设筒子纱的质量范围在[1 700,2 300]区间内，每包筒子纱的质量为25 kg。

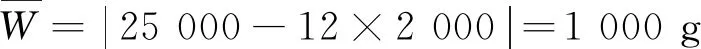
可见，当1包筒子纱在给定范围内随机抽取 12个时，总误差高达1 kg，与规定的60 g相差甚远，已经远远超过了配重的要求，而纺纱企业中采用人工配重方式，效率低下，因此，要研究如何实现快速稳定的筒子纱配重方法。

3.2 配重原理

筒子纱配重原理主要是已打包的筒子纱的质量加上当前正在计算的筒子纱和从4个立体库中能找出的筒子纱，在质量上能达到[Yw-ε,Yw+ε]，Yw为25 kg，ε为60 g，在数量上能达到12个筒子纱，则认为当前的筒子纱满足配重要求。

具体步骤如下，起始储纱模式已准备就绪，进入实际配重模式，实际配重模式如图3所示。

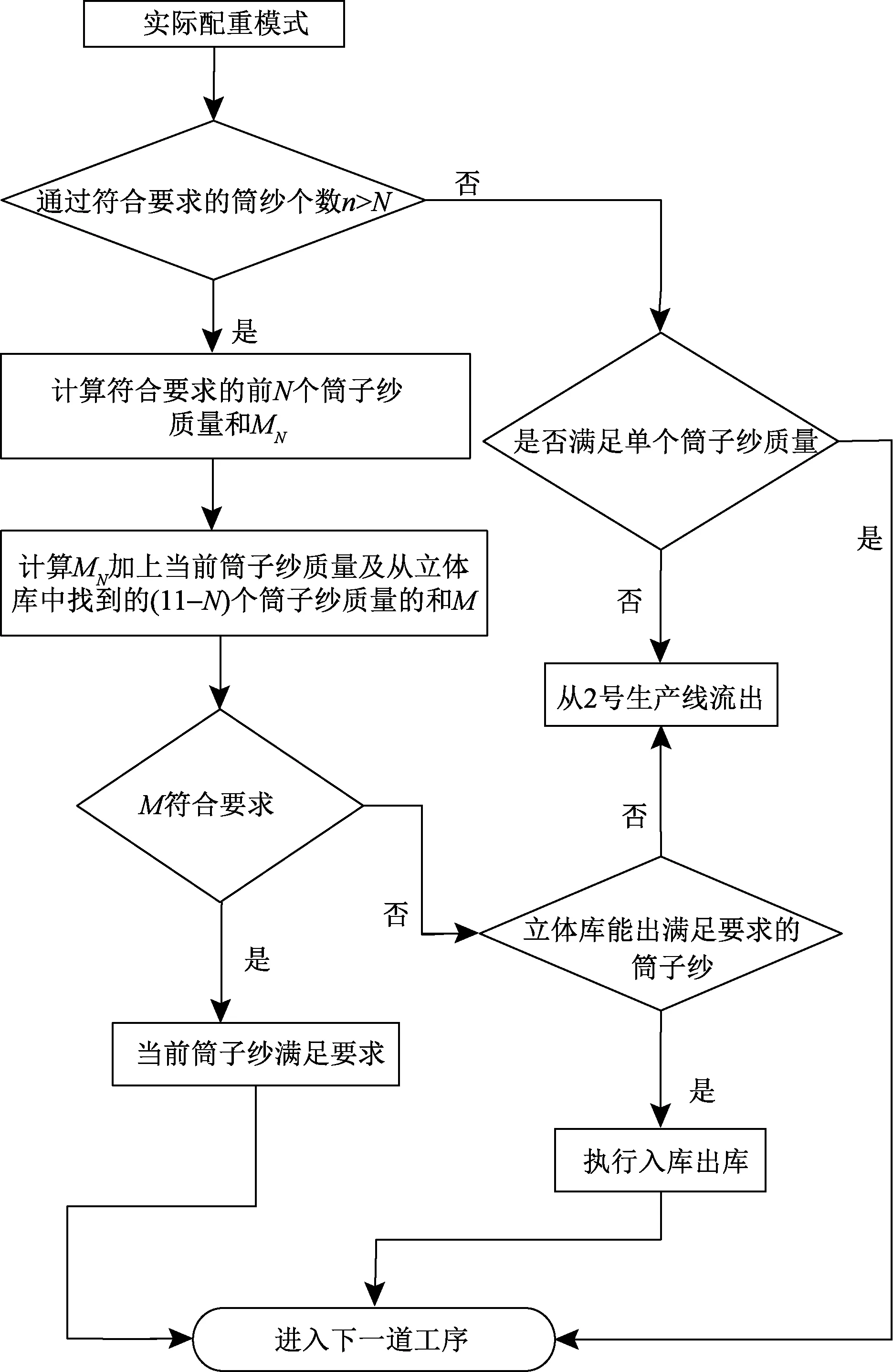
图3 实际配重模式流程图Fig.3 Actual counterweight mode flow chart

1) 当前一包的第1个筒子纱由1号生产线进入动态秤称量(动态秤的误差在2 g左右)，在满足给定的单个筒子纱质量的条件下，直接从2号生产线进入4号生产线参与下一步执行动作，并记录该筒子纱的质量。之后继续进行第2个筒子纱的动作执行，一直到给定的N(N≤10，N越接近12则越难配重)个。这时已经有N个筒子纱在满足单个筒子纱质量的条件下进入后续的包装工序。

2) 当第N+1个筒子纱经过动态秤时，将这个筒子纱的质量传给控制单元，先加上前面已经符合要求的N个筒子纱的质量和MN，然后从立体库存储的4YN个筒子纱中寻找(11-N)个筒子纱，将其质量和M11-N与N个筒子纱的质量和MN和当前第N+1个筒子纱的质量相加的总质量M，使M满足[Yw-ε,Yw+ε]，ε为配重精度，一般固定不变为 60 g，则认为当前第N+1个筒子纱满足配重要求，可以从2号生产线进入4号生产线执行下一道工序。

3)若M不满足[Yw-ε,Yw+ε]时，则当前第N+1 个筒子纱不符合要求。用Yw总质量减去前N个筒子纱的质量和MN再除以(12-N)，从立体库中找出质量在[(Yw-ε-MN)/(12-N),(Yw+ε-MN)/(12-N)]之间的筒子纱，若能找出这样的筒子纱，则该筒子纱出立体库，当前第N+1个筒子纱进入立体库。

4)若找不出符合要求的筒子纱，则当前第N+1个筒子纱从2号生产线末端掉出生产线，不再参与配重。

在筒子纱入库时，要判断该筒子纱在轻、正常、重3个区间的哪个区间，再根据立体库的实际情况从而判断应进入哪个立体库。使每个立体库中的筒子纱尽可能分布均匀，与此同时尽量避免与出库的立体库同，保证能持续不断地进行配重以此提高效率。

4 配重方案处理

在实际配重模式中，每个当前筒子纱经过匹配点时都要进行一次配重方案上的计算，因此就要求控制系统在算法上要提高效率。按照筒子纱最多48个计算，从48个筒子纱中取出n(n≤12的自然数)个，最多的可能有百亿多种方案(C(48,12)=6.9×1010)，表1示出从48个筒子纱中取出1到12个筒子纱的最多计算次数。因此，算法开始部分不直接采用排列组合[8-9]的方式进行计算，而是采用人为设定优化后的方案进行计算。

首先，对立体库中的筒子纱按质量从小到大排列。立体库中筒子纱最多的时候有48个，冒泡排序的时间复杂度较高，效率慢，因此在排列方式上采用选择排序，比冒泡排序需要的时间相对较少。选择排序是每次从待排序的筒子纱质量中选出最小的一个质量，存放在序列的起始位置，然后再从剩余未排序筒子纱质量中继续寻找最小筒子纱质量，放到已排序序列的末尾，以此类推直至全部待排序的筒子纱质量排完。在立体库中筒子纱按质量排序完成后，之后的筒子纱进出就可以按照链表的的方式插入或删除，从而进行再一次排序。

表1 实际配重模式下排列组合算法各种 情况的方案次数Tab.1 Number of alternatives in actual counterweight mode under different circumstances

区间分布法如图4所示，在48个筒子纱按质量从小到大排列好后，再平均分成4个区间，从这4个区间中的每个区间选出n(n≤12的自然数)个，这时的计算量大大减少。从左到右筒子纱的质量从小到大排列。若能找出符合要求的筒子纱，则当前第N+1个筒子纱满足包装要求，减少了直接进行排列组合计算的时间。

图4 区间分布图Fig.4 Interval distribution map

若还是不能找出n个筒子纱，则采用质量配对原则。质量配对法如图5所示，即保证找出的2个筒子纱其质量相加的平均值与n个筒子纱质量的平均值接近。n为偶数时，需要找到n/2对筒子纱。n为奇数时，先找到(n-1)/2对，再找到一个与平均值接近的筒子纱。然后再进行后续的计算判断是否满足。其中质量配对原则要对质量范围进行对称划分成多个区间。根据n个筒子纱的平均质量，向两边开始划分区间。设筒子纱的质量服从均值为n个筒子纱的平均质量Δx，方差为σ2的正太分布。x1，x2是距离Δx相差l的2个点，这2个点的概率密度分别为ρ(x1)，ρ(x2)，|x1-x|=|x2-x|=l，ρ(x1)=ρ(x2)，Δx1=Δx2，如图5所示。这样区间就可以分成3部分：轻区间，正常区间，重区间。

图5 正态分布图Fig.5 Positive distribution map

正常区间为(a,b)，轻区间为(a-(m+1)r,a-mr)，重区间为(b+nr,b+(n+1)r)，其中a为n个筒子纱质量平均范围的最小值，b为n个筒子纱质量平均范围的最大值。r为分区间间隔值，单位是kg。轻区间的分区间与重区间的分区间一一对应，在轻区间的分区间取出筒子纱，则要从与之对应的重区间的分区间再取出一个筒子纱，使2个筒子纱能进行配对。

若以上方法都不能找出n个符合要求的筒子纱，则采用排列组合法计算结果，排列组合法就是从48个筒子纱中取n个，C(48,n)，然后结合递归算法得到符合要求的n个筒子纱。用该方法最终判断能否找出n个筒子纱，即第N+1个筒子纱是否符合要求。若未能找出n个筒子纱，则第N+1个筒子纱不再参与配重，从2号生产线上流出整个系统。

5 仿真与实验结果

根据以上配重原理及配重方案[10]，编写仿真程序。用随机函数rand()产生一个4位数的各个位，其中千位规定为1或者2，得到符合单个筒子纱质量要求筒子纱，输出参数为筒子纱配重效率，即成功配重的筒子纱个数与总共的筒子纱个数比值的百分数。表2示出采用区间分布法(方法a)，区间分布法及质量配对法(方法b)，区间分布法、质量配对法及排列组合(方法c)对3种配重方法的实验结果影响。

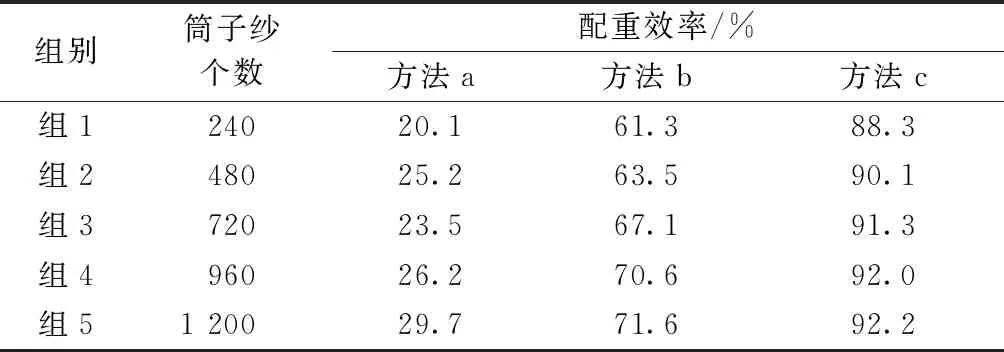
表2 不同配重方法的实验结果影响表Tab.2 Influence of experimental results of different weighting methods

由表中仿真结果可知，采用区间分布法的效率非常低，大部分筒子纱无法配出。加入质量配对法之后，配重效率有了较大的改善，但还是有一部分筒子纱无法完成配重。最后加入排列组合，计算筒子纱配重的所有可能性。由此可见，采用排列组合能完成所有可以完成的配重，但考虑到时间问题，还是要先采用区间分布及质量配对法，最终效率能达到90%以上，所有配重方法累加的计算时间大约为 4 s，但并不是每个筒子纱都要进行所有配重方法计算。经生产线大量实验验证，1包筒子纱(12个)从流水线上开始配重到装袋，时间不超过70 s，满足生产线速度的要求，证明本文的配重方案是正确可行的。

6 结束语

根据筒子纱包装的任务需求，确定了筒子纱配重方案。考虑配重结果以及配重效率等原因，采用区间分布、质量配对和排列组合等方法对筒子纱进行配重处理。通过理论分析和实验仿真，本文提出的筒子纱配重包装方案设计合理。设计的系统适用于筒子纱在流水线上打包的应用，能自动、准确、高效地进行配重、打包等工作，操作简单、灵活，减少了人力，提高了整个生产行业的自动化水平，具有良好的工程应用前景。