基于偏振成像的低光照强背景噪声下的目标位姿估计
张 然,桂心远,成昊远,褚金奎
(大连理工大学辽宁省微/纳米技术与系统重点实验室精密与特种加工教育部重点实验室,辽宁 大连116024)
1 引言
物体位姿信息在航空、航海、室内机器人定位等领域都有着十分重要的地位[1-2]。为了保证在各种工况下目标位姿的实时可控,对物体位姿进行精准测量是必要的,这也对物体位姿测量技术提出了更高的要求。位姿测量主要针对物体的6个自由度进行检测:俯仰角、偏航角、翻滚角以及X,Y,Z3个方向上的位移。与惯性测量位姿和雷达测量位姿相比,视觉测量位姿具有非接触、直观性强、测量精度较高、抗电磁干扰能力强、结构简单、测量成本低等优点,因此广泛应用于实际工程测量中[3-5]。Xu等人在室内环境下借助天花板来求解相机的位姿[6]。Zhao等人对比研究了常用的基于LED照明的方法[7]。Yin等人研究了基于单目成像系统的平面目标测量[8]。Li等人以ArUco码作为参照物测量物体的相对位姿[9]。但是在低光照条件下,比如夜间与水下,计算机视觉测量技术遇到了较大的挑战。
在自然界中,生物偏振视觉很常见,如沙蚁可以利用天空偏振光进行导航并找到自己的巢穴[10]。而在几乎全黑的水下环境中,鱿鱼和螳螂虾都具有偏振视觉,它们能在极暗的环境中捕猎和藏匿[11-12]。偏振光具有“弱光强化,强光弱化”的特点,这正是众多弱光环境下生物依赖偏振视觉的原因[13-14],即偏振光作为信息载体,其偏振度及偏振角等信息相较光强信息具有更高的强度,传输距离远,特别适合在低光照环境中进行传递[15]。利用偏振成像技术,可有效提高低光照下的可见度,从而求解运动物体的位姿信息。已有大量研究证明了在大雾和水下等复杂环境中使用偏振成像的优异性[16-22],偏振成像获得的图像更加清晰并且可视距离更远,极端情况下甚至能恢复出光强图几乎看不到的细节。本文提出了一种基于偏振成像的低光照强背景噪声环境下的物体位姿求解方法,针对设计的四偏振光源目标提出了一种有效的识别算法,使用偏振成像来识别目标的4个定位点,进而估计目标的位姿参数。后续实验中对比了偏振图与光强图,并验证了算法的性能。
2 偏振成像模型
偏振成像常使用的方法有分时法、分振幅法和分焦面法等。本文使用的是分焦面成像法,采用的偏振相机一次成像可以获得4张不同偏振角度的光强图像,其偏振角度分别为0°,45°,90°和135°。
光波偏振属性的数学表达一般采用斯托克斯矢量。在斯托克斯矢量表示方法中,光波的偏振属性可以用4个实数来描述,即:
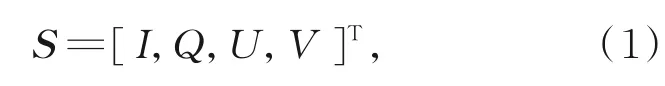
式中:I是投影在成像传感器上的光强,Q是0°和90°方向偏振分量的光强差,U是45°和135°方向偏振分量的光强差,V是左旋和右旋圆偏振分量的光强差。一般情况下,分量V可以忽略。因此,若假设光源的斯托斯矢量表示为S,当偏振器的主透光轴与设定的零度参考线之间的夹角为Ψ时,偏振器对原光波偏振属性的改变可以用MULLER矩阵表示,即有:

因为相机可以直接测量的是光强I,所以可以利用MULLER矩阵的第一行。即:

假设Ψ角度选取0°,45°,90°,得方程组:

整理得:

求得线偏振度为:

由此便可以通过一次成像中的0°,45°和90°图像计算出线偏振度(Degree of Linear Polariza⁃tion,DoLP)。
3 目标位姿求解
相机的成像模型即中心透视成像模型,其基本原理如图1所示。三维物体投影到相机的成像平面上,量化后最终获得离散的二维图像。单相机成像时,由于存在三维向二维的不可逆变换,没有辅助信息时无法从图像推算出物体的位置以及姿态。为了从单张图解算出其中物体的位置和姿态,需要知道相机的内参数以及在物体上做一个已知参数的标记。本文采用4个点作为标记的方法,如图1所示,由OtXt,OtYt,OtZt构成的三维坐标系为现实世界中目标物体的坐标系,A′,B′,C′,D′为目标物体上的4个标记点,其中有OtA′=OtB′=OtC′=OtD′。有OiXi和OiYi构成的二维坐标系为相机成像的图像坐标系,A,B,C,D为目标物体上的标记点投影到图像上的点。Oc为中心透视成像模型中的透视原点,相机的焦距即为f=OcOi。已知相机每个像素点的实际尺寸,这样在图像坐标系下可以计算出A,B,C,D4个点的实际坐标。

图1 中心透视成像原理Fig.1 Principle diagram of central perspective imaging
通过以上参数和成像模型,根据余弦定理可以求出目标物体的位置和姿态:

其中:α,β和γ分别代表∠AOcB,∠BOcC,∠COcA,通过对应的像素坐标可以求得;a,b和c分别代表A′B′,B′C′,C′A′的长度;x,y,z分别代表OcA′,OcB′,OcC′的长度。根据式(7)即可求得x,y,z,然而该方程具有多解,所以需要第4个点来求得唯一解。
已知A,B,C在图像坐标系的坐标,利用x,y,z可求得A′,B′和C′在图像坐标系的坐标。最后,利用坐标转化矩阵可求得相机相对于四光源的位姿。如下式:

其中:T X,T Y,T Z分别为相机相对于光源X,Y,Z方向的位移;θ,φ,μ分别为绕X轴,Y轴,Z轴的旋转角度,逆时针为正;(X,Y,Z)是四光源在世界坐标系下的坐标,(X′,Y′,Z′)是四光源在相机坐标系下的坐标。
在低光照室外的环境下,不发光的传统标记将无法使用。若使用4个普通的LED灯作为标记,则可以在低光照的环境下使用,但是在室外很可能存在人造灯光的干扰,导致无法识别。本文将4个普通LED光源更换成4个偏振LED光源,配合偏振相机来解决低光照室外使用所遇到的问题。如图2所示,在4个偏振光源上安装一层线偏振片,经过线偏振片的LED光便成为线偏振光。理论上来说,出射的光线是完全线偏振光,但由于线偏振片无法达到完美的效果,加上透过空气后,光线的偏振状态会略微发生变化,实际由4个偏振光源到达偏振相机的光线并非完全线偏振光,即其偏振度略小于1。即便如此,相较于自然光和一般人造光源,本文中偏振光源的偏振度更大。并且偏振光具有“强光弱化,弱光强化”的特点,不需要很高功率的LED灯也能在远距离保持一定的偏振度,更具有经济效益。

图2 基于偏振成像的目标位姿估计实验示意图Fig.2 Schematic of target pose estimation based on po⁃larized imaging experiment
如图2所示,偏振相机拍摄含有四偏振光源的图像,在图像中提取的4个偏振光标记后,使用计算机计算出目标物体的位置和姿态,其算法流程如图3所示。
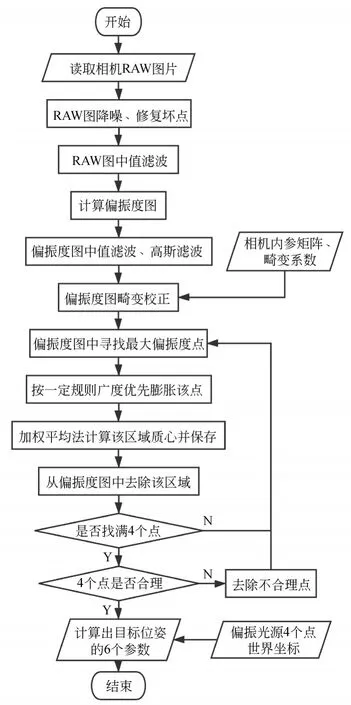
图3 目标识别与位姿估计算法流程Fig.3 Flow chart of target recognition and pose estima⁃tion algorithm
在提取目标点以前,首先应该考虑低光照环境下暗电流、热噪声、坏点等成像问题对图像质量的影响[23-24]。在低光照环境下,成像后图像上像素的灰度值都很低,此时CMOS上暗电流的影响会被放大,考虑到偏振相机拍摄的原图(下称RAW图)将用来计算偏振度图,本文采用阈值法减少暗电流对偏振度图的影响。拍摄多张RAW图并计算偏振度图后,对比发现像素的灰度值选取2作为阈值点能兼顾降噪和保留细节信息,即RAW图中所有像素灰度值小于2的点都将它们改为2。而在上述对比还发现了坏点问题,即每张图片都有固定的像素点出现异常值。本文采用“屏蔽+插值”的方法,即将该点异常值舍弃,根据周围像素插值出新的值去代替异常值。
上述处理后,低光照环境下图片依然有较为明显的噪点,这会影响4个偏振光源的识别。对此问题,本文提出“两次滤波”的降噪方法。偏振相机一次成像可获得4张不同偏振角的RAW图像,由其中3张即可计算出所需的偏振度图,故分别在RAW图和偏振度图上进行滤波,就可以改善最终偏振度图的成像质量,使得后续识别4个偏振光源更加精确。中值滤波应对椒盐噪声的效果很好,高斯滤波可以让图像梯度更加平缓。本文在RAW图中使用中值滤波,在偏振度图中使用“中值滤波+高斯滤波”的方式。降噪效果对比如图4所示,可以看到本文的方法能够将目标从背景中有效地分离出来,并且目标更加平滑,易于识别。由于镜头制造安装等误差,实际拍摄的图像存在畸变、扭曲等问题,这会显著影响目标物体的位姿计算精度,故需要对这些误差进行标定。本文以张正友提出的基于平面靶标标定方法为基础[25],并考虑到制造时镜头畸变及其他因素的影响,基于小孔成像模型求解出相机的内、外参数和镜头畸变系数并保存起来,后续就能随时校正图像。

图4 降噪效果对比Fig.4 Comparison of noise reduction effects
4个偏振光源的偏振度很高,但在偏振度图中每个光源会形成一片偏振度很高的区域而不是点,故在偏振图中识别出4个最高偏振度且偏振度大于一定阈值的区域即可认为识别到了目标偏振标记。识别时按偏振度从大到小依次识别4个区域。识别偏振光源时,先在偏振度图中寻找最大的偏振度点,再按偏振度不低于最大偏振度70%的阈值去按广度优先算法膨胀最大偏振度区域,这样就找到了一个区域。然后将该区域保存起来,并在偏振度图中将该区域的偏振度设为0,以便在接下来的循环找点中排除该区域。按上述规则循环4次,即可找出偏振度图中偏振度最大的4个区域。为了提高识别精度至亚像素级,使用加权平均法计算每个区域的质心作为最终识别的偏振光源坐标点。在空气中,由于散射等原因,偏振光源的偏振度随着传播距离的增加会有一定程度的衰减。考虑到远距离成像时可能会存在干扰,最后在算法中加入纠错部分来增加识别的准确率。纠错部分为:识别出4个点后,若4个点形成的四边形有两条边长明显长于另外两条边长,意味着此时两条最长边交点为离另外3个点异常远的异常点,则剔除异常点所在区域,重新寻找下一个候选区域;进而重新开始一轮循环。
4 实验
为证明本文方法的优异性和算法的有效性,选择低光照强背景噪声环境下进行实验。偏振相机的型号为PHX050S-PC,相机分辨率为2448×2048,每个像素的物理尺寸为3.45μm,镜头焦距为10.5 mm,四偏振光源距离中心0.1 m,在固定好的4个LED上方分别固定一块线偏振片组成四偏振光源,每个LED的功率约为5 mW。偏振相机拍摄图像后,由它所连接的笔记本电脑计算接收数据并完成计算。将偏振相机调平并固定,分别在距离偏振相机约5,20,40 m的地方拍摄四偏振光源。图5为四偏振光源距离偏振相机约40 m远时的场景图,可以看到拍摄背景存在大量居民楼灯光以及路灯的干扰。由于LED功率有限,随着目标与相机的距离增加,光强图中四偏振光源相对背景噪声越来越不明显,识别难度增大。

图5 偏振相机视角下的实验场景Fig.5 Experimental scene from perspective of polariza⁃tion camera
5 结果与讨论
5.1 偏振成像优势
图6所示为不同距离下四偏振光源的光强图和偏振度图以及识别结果。可以看到在光强图中四偏振光源都很难辨认,而在偏振度图中四偏振光源都很清晰,并且3个不同距离情况下算法都成功识别出4个光源位置。每组曝光时间相同,远距离时适当提高了曝光时间。

图6 光强图与偏振图识别结果对比Fig.6 Comparison of recognition results of illumination and DoP images
为了进行定量对比,本文引入参数K:

其中:V代表图像中的像素,在光强图中代表亮度,在偏振度图中代表线偏振度;Vmin表示图像中四偏振光源区域中最暗区域的最大值,此处选择最暗光源区域像素的最大值是因为本文提出的算法基于最大值提取光源区域,故Vmin代表四偏振光源中最暗的那个光源,Vmax表示四偏振光源以外背景区域的最大值,代表背景中的最大噪声。K为最暗光源与背景最大噪声之比,代表四偏振光源相较于背景噪声的显著度。K值越大,即四偏振光源区域整体越显著;K值越小,四偏振光源区域就越难在背景中区分出来。当K>1时,本文提出的算法可以识别四偏振光源;当K<1时,存在一个最暗的偏振光源区域,该区域比背景噪声小。虽然本文提出的算法中有纠错部分,但此时有可能识别失败,并且K越小,识别成功率越低。分别计算光强图和偏振度图的K值,如图7所示。

图7 光强图和偏振度图的K值Fig.7 K of illumination and DoP images
由图7可知,5 m时光强的K值大于偏振度,这是因为近距离下LED的亮度远高于背景亮度;而随着距离增大,相机接收到的LED亮度变小,到20 m时光强的K值降至0.93,远小于偏振度,并且K<1,此时四偏振光源中最暗的光源已经很难从背景中区分开来;40 m时光强图的K值继续降至0.58,依然远小于偏振度图,此时K值远小于1,这意味着在光强图中很难从背景中区分四偏振光源。随着距离的增大,光强图的K值迅速下降,而偏振度图的K值虽然也在下降,但其下降缓慢,并且一直保持在1以上。而观察图6可以发现,光强图中4个光源区域亮度差异很大,这是因为LED发出的光有一定的方向性,光源的略微倾斜都会导致光强图中出现这种情况。考虑到这一点,这里统计了光强图和偏振度中4个光源区域亮度的方差(对应的光强图和偏振度图数值已做归一化处理),如表1所示。可以发现,在不同距离下光强图的方差都高于偏振图,5 m时光强图的方差是偏振度图的10.8倍。而偏振度图的方差比较稳定,这也和K值的结果相吻合。K值和方差的对比证明了本文提出的偏振方法精度更高且鲁棒性更强。
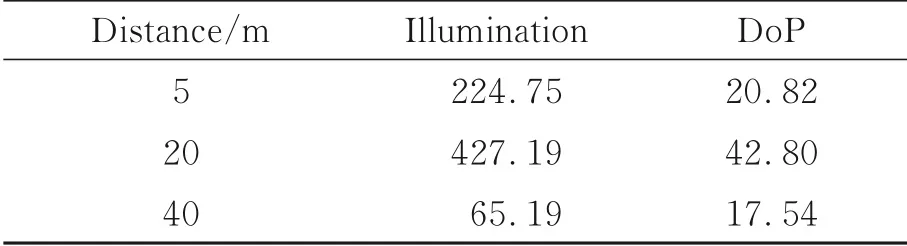
表1 四光源区域亮度方差Tab.1 Variance of brightness in area of 4 light sources
5.2 位姿精度
由于四偏振光源的安装误差以及实验时光源相对相机的角度难以精确控制(特别是在远距离),而且解算出的6个位姿参数是耦合的,相对角度的误差会影响相对位置的精度,但不会影响四偏振光源与相机的距离精度,且算法的迭代性使得角度误差极小,故本文以四偏振光源距离相机的直线距离来衡量识别的位姿精度。

表2 位姿精度Tab.2 Pose accuracy
由表可知,随着距离的增加,相对误差变小,这是因为近距离时每个光源在图像中区域占比较大,这就导致识别光源的像素精度不高,进而导致相对误差较大;而远距离时每个光源成像区域较小,识别光源的像素精度较高,也就减小了相对误差。
5.3 像素识别误差
光源的像素识别误差是理论像素与识别像素的位置差,它对位姿识别的影响结果如表3所示。由上文分析得知,像素识别误差与光源成像区域面积有关。假设光斑成像区域靠近图像中心,由如图1所示的相机成像模型可估算光源区域在图像中的直径为:

表3 像素识别误差及其导致的位姿估计误差Tab.3 Pixel recognition errors and corresponding pose estimation errors

其中:l为光源光斑的物理尺寸,L为光源与相机的距离,f为相机焦距。假定l不变,那么图像中光斑尺寸仅与1/L成正比,故可认为图像中光斑识别误差也仅与1/L呈线性关系,则有:

用式(11)来估算像素识别误差,其中a和b为待估计参数,使用5,20,40 m的误差数据拟合后便可估计出a和b的值,进而估计出70 m和100 m的像素识别误差。
6 结论
本文提出了一种受生物启发的方法,利用偏振光源在低光照强背景噪声环境下计算目标的位姿。该方法基于偏振成像技术,在保持传统光学精度的前提下,拓宽了适用范围并且增强了识别的鲁棒性。实验结果表明,提出的识别算法降噪能力强,抗噪声效果好,识别准确度高,在3个距离下均识别成功,40 m远时位姿估计误差为2.99%。此外,该方法简单易行、成本较低,只需带有偏振片的4个低功耗LED光源作为目标特征。未来的工作将集中在降低像素误差和提高使用范围上。

