回焊炉电路板焊接炉温曲线优化模型
徐宗煌, 徐剑莆, 李世龙, 林慧雅
(福州理工学院 a. 应用科学与工程学院, b. 计算与信息科学学院, c. 商学院, 福建 福州 350506)
在生产集成电路板等电子产品的过程中,需要将各种电子元件的印刷电路板在回焊炉内进行焊接.通过加热的方式将电子元件自动焊接到电路板上.在此过程中,对回焊炉内的温度、电路板两侧传送带的速度和电子元件的焊接时间等因素有着严格要求,对产品质量至关重要.实际生产时可以通过调节各温区的设定温度和传送带的过炉速度来控制产品质量.目前,这方面的许多工作是通过实验测试来进行控制和调整的.
现阶段,国内外对于回焊炉电路板焊接炉温曲线已经开展了一系列的分析研究.在国内,席晨馨[1]利用微分方程模型,同时结合模拟退火算法,对炉温曲线的优化设计进行了研究.汤宗健等[2]通过对回流焊炉温曲线的管控与分析,对加强回流焊炉各温区温度的监控提出了一系列有针对性的措施.孟祥[3]则针对不同生产工况切换下的加热炉炉温优化方法进行了分析研究,得到最佳炉温分布曲线.丛铭智等[4]利用机理预测替换传统经验法,在回流焊机理分析和热力学分析的基础上对炉温曲线控制方法展开了相关研究.而国外的Iqbal等[5]对回流焊在母板应用中的柔性印刷电路板温度预测,并对回流曲线的温度分布进行了优化.Lempinen等[6]利用有限元仿真软件和实验环境下,分别研究不同加热时间常数对回流炉的焊接炉温曲线峰值焊接温度的影响.Hegde等[7]采用有限元分析方法研究回炉焊中温度分布不均匀对焊点结构响应的影响.Srisertpol等[8]提出了一种基于系统辨识方法的加热炉步进梁型数学模型,从而对加热炉的温度进行控制.
通常情况下,回焊炉内部设置若干个小温区,它们从功能上可分成4个大温区:预热区、恒温区、回流区、冷却区.电路板两侧搭在传送带上匀速进入炉内进行加热焊接.某回焊炉内有11个小温区及炉前区域和炉后区域,如图1所示.每个小温区长度为30.5 cm,相邻小温区之间有5 cm的间隙,炉前区域和炉后区域长度均为25 cm.另外,生产车间的温度保持在25 ℃.

图1 回焊炉截面示意图Fig.1 Schematic diagram of cross section of reflow furnace
本文基于牛顿冷却定律和微分思想,分别建立焊接区域传热机理模型、传送带过炉速度优化模型以及峰值温度覆盖面积优化模型,对回焊炉电路板焊接炉温曲线进行一系列优化分析研究.
1 焊接区域传热机理模型
1.1 模型分析
首先分析已知数据,找出电路板焊接区域中心与环境温度温差的大小对于其吸收热量多少的影响规律.运用微分方程[9-11]的思想构建数学模型,根据已给出的数据,将电路板在焊接过程中的时间、速度和温度变化写出相应的微分关系式.再根据数据拟合的图像进行分段分析,导入电路板运动的时间,改变各温区的温度,代入数据即可求出电路板在回焊炉内的位移与焊接区域中心温度的变化关系.从而列出不同传送带过炉速度与温区温度情况下,电路板焊接区域中心的温度变化情况,主要思路如图2所示.
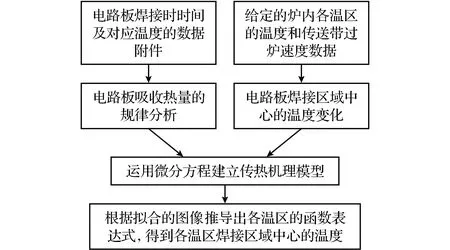
图2 焊接区域传热机理模型主要思路Fig.2 Main ideas of heat transfer mechanism model in welding zone
1.2 模型建立
1.2.1 电路板吸收热量的规律分析
根据已经给出的附件,找出电路板焊接区域中心与环境温度温差的大小对于其吸收热量多少的影响规律.为便于后续计算,先将自变量即电路板在焊接过程中的运动时间t用速度位移公式s=vt进行转换,设电路板在焊接过程中的位移为x.转化后为x=vt,表示为
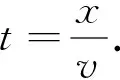
(1)
为求电路板焊接区域中心与环境温度温差的大小对于其吸收热量多少的影响,设电路板在焊接过程中的环境温度θ0,时间为t时焊接区域中心的温度为θ(t),此时环境温度与电路板焊接区域中心温度的温度差表示为Δθ(t).其表达式为
Δθ(t)=θ0-θ(t).
(2)
通过分析附件中的数据,可以得到电路板在焊接过程中的位移x与电路板焊接区域中心温度θ(x)的关系,由此可以求出电路板位移与温度的变化量.运用微分方程的思想,建立关系式
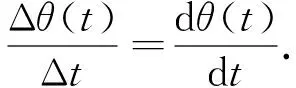
(3)
联立式(1)和式(3)得到的函数关系式为

(4)
根据式(4)进行数据处理,可以画出附件数据条件下的炉温曲线,据此进行下一步分析.
1.2.2 电路板焊接区域中心的温度变化分析
通过以上分析可知,电路板在已知温区和相应传送带速度的情况下的温度变化情况.将实验数据的速度v=78 cm·min-1单位化成cm·s-1,即v=1.3 cm·s-1.根据传送带的过炉速度和电路板的运动时间t计算出电路板在各个时刻的位移.因为模型中电路板速度大于原电路板速度,所以若继续运用时间t作自变量则会导致图像温度与电路板运动位置的不匹配,造成计算误差.所以要将自变量时间t通过式(1)进行替换,以位移x作为自变量.
根据附件中的数据,将实验数据中各温区的温度与原数据各温区的温度进行比较差值,对应加减相应的温度即可求出相应的炉温曲线.
1.3 模型求解
1.3.1 电路板吸收热量的规律求解
根据式(4),将附件中的数据进行数据拟合.为便于分析,根据原数据的各个温区温度画出了环境温度与炉温曲线,如图3所示.

图3 原数据条件下电路板焊接的环境温度与炉温曲线Fig.3 Ambient temperature andFurnace temperature curve of circuit board welding under original data conditions
通过对图3分析可知,电路板温度与环境温度的温差越大时,电路板的吸热能力越强.当电路板温度越接近环境温度时,电路板的吸热能力越差.
电路板在各个温区吸收热量的能力不同,且差异较大.所以要求出电路板焊接过程中的炉温曲线,就要分温区进行数据分析和拟合.
1.3.2 电路板焊接区域中心的温度变化求解
附件是某次实验中炉温曲线的数据,传送带的过炉速度为70 cm·min-1,各温区设定的温度分别为175 ℃(小温区1~5)、195 ℃(小温区6)、235 ℃(小温区7)、255 ℃(小温区8~9)及25 ℃(小温区10~11);而给定的传送带过炉速度为78 cm·min-1,各温区温度的设定值分别为173 ℃(小温区1~5)、198 ℃(小温区6)、230 ℃(小温区7)和257 ℃(小温区8~9),整理如表1所示.

表1 各温区附件数据与实验数据的温度及变化量
根据表1中的温度变化量进行数据处理, 将各个温区原有的电路板焊接区域中心温度传感器感受到的温度对应加减相应的温度变化量. 对该列数据进行数据拟合, 以电路板在传送带上的位移x为自变量, 以位移为x时焊接区域中心的温度θ(x)为因变量, 进行2次项曲线拟合.得到的拟合图像如图4所示.

图4 传送带速度为78 cm·min-1及其 对应温区下的炉温曲线Fig.4 Furnace temperature curve at a conveyor speed of 78 cm·min-1 and its corresponding temperature zone
根据图4所拟合的图像,反向推导出各温区的函数表达式,由于拟合的图像是由所求数据拟合而成,所以会有一定的误差,推导出的各温区的函数表达式如下:

(5)
接着根据式(5)拟合出的函数表达式,代入相应的温区位移,即可得到小温区3、6、7中点及小温区8结束处焊接区域中心的温度,如表2所示.

表2 各温区焊接区域中心的温度
由于炉前温度的拟合函数与实际情况误差较大,本数据拟合出的进入小温区1时电路板的温度为25.33 ℃,又考虑从运动开始时0 s至运动到小温区1时16.5 s正好有32个数据,假设此段时间内电路板的吸热能力恒定,温度变化率相同,即每过0.5 s温度升高0.01 ℃.
最后根据拟合的函数,将位移x根据式(1)代换成位移时间t的函数,代入对应的点坐标,即可求出电路板从炉前区域匀速运动至炉后区域全过程的焊接区域中心的温度数据.
2 传送带过炉速度优化模型
2.1 模型分析
假定各温区温度的设定值分别为182 ℃(小温区1~5)、203 ℃(小温区6)、237 ℃(小温区7)、254 ℃(小温区8~9),要求确定允许的最大传送带过炉速度,就必须满足制程界限的约束条件.如果速度过快,会使电路板的加热时间不足,从而导致在升温过程中在150~190 ℃的时间及温度大于217 ℃的时间不足,以及电路板在温度上升和下降的过程中的斜率过大,从而导致电路板上电子元件的焊接不稳定.若传送带的过炉速度过低,则会导致超出上述2个界限的范围时间.同时要合理地控制电路板加热的峰值温度保持在240~250 ℃之间.
速度的不同会导致在各个界限中数据的不同,要想求出允许的最大传送带过炉速度,就需要计算大量的不同速度情况,并判断其是否满足制程界限.因此该模型根据多重搜索算法对传送带过炉速度进行搜索求解,主要思路如图5所示.

图5 传送带过炉速度优化模型主要思路Fig.5 The main idea of the conveyor belt passing furnace speed optimization model
2.2 模型建立
2.2.1 电路板焊接区域中心温度分析
要确定允许的最大传送带的过炉速度,就要先确定约束条件的约束区间如何计算求解,因此运用牛顿冷却定律[12-14]进行温度变化的求解.牛顿冷却定律的表述为系统温度损失速度与系统和环境的温差θ环成正比,设比例系数为k,其方程表示为

(6)
将式(6)求解可得到焊接区域的中心温度与电路板在传送带上运动时间的函数关系式,设函数中e指数的系数c为常数,则其表达式为
θ=θ环+ce-kt.
(7)
为便于后续计算,求出电路板焊接区域中心温度的分段函数表达式θ.为求电路板在焊接过程中焊接区域中心的温度变化情况,仍需要引用附件原数据进行数据拟合.联立式(6)与式(7),可表示出电路板焊接区域中心温度的函数表达式,其函数关系为

(8)
由式(8)可知,求出相应的常数c和k后,即可得到电路板焊接区域中心温度的分段函数表达式θ,从而进行相应制程界限约束条件下的求解.
2.2.2 制程界限约束条件分析
在回焊炉电路板焊接生产中,炉温曲线应满足一定的要求,称为制程界限,如表3所示.

表3 制程界限Table 3 Process boundary
根据表3的数据可知,制程界限有5个约束条件,分别是温度上升斜率、温度下降斜率、温度上升过程中在150~190 ℃的时间、温度大于217 ℃的时间和峰值温度.如何分析这些约束条件的限制情况成为了解决本模型的关键.
假设此时已得到电路板焊接区域中心温度的分段函数表达式θ.要计算最终的最大传送带过炉速度vmax,再分析制程界限的各项约束条件.可先假设一个初速度进行代入求值,后分别计算制程界限的限制条件,如计算第3条电路板在温度上升过程中在150~190 ℃的时间要求.先计算电路板焊接过程中当θ=150 ℃时的时间t1,再计算焊接过程中当θ=190 ℃时的时间t2,计算t2-t1差值,若此差值位于60~120 s之间,则满足第3条制程界限的限制条件.计算第4条制程界限时,需要求出当θ=217 ℃时的时间t1和t2,同样计算t2-t1的值是否在40~90 s之间.计算第5条制程界限时,需要根据第9段小温区末尾的位移值344.5 cm代入θ的表达式中计算峰值温度,若此温度处在240~250 ℃之间,则满足第5条制程界限的限制条件.最后根据拟合出的电路板焊接区域中心温度的分段函数表达式θ再判断是否符合第1、2条制程界限的限制条件.
运用多重搜索算法计算不同传送带的过炉速度vmax,根据制程界限的约束条件进行筛选,当各项条件都满足且求得的速度最大时,即可确定允许的最大传送带过炉速度vmax的值.
2.3 模型求解
2.3.1 牛顿冷却定律的求解
根据牛顿冷却定律式(6)及其解的表达式(7),可先求出常数k.运用两边同时取对数的方法进行化简,其导出的关系式为
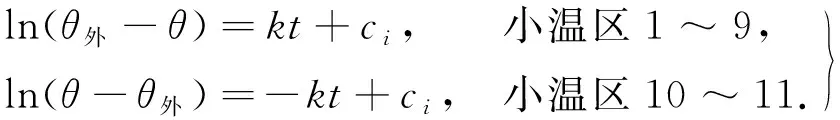
(9)
因为不同温区的时间和温度都不同,所以把函数写成分段函数,代入对应的温度和时间的数据可以得到每段函数对应的常数c,最终就可以得到一个完整的分段函数θ.
接着将对应的区间温度代回式(9),即可得到时间t与电路板焊接区域中心温度θ的函数关系式.根据式(1)将时间t和位移x进行转化.再根据表3给出的制程界限,把速度区间65~100 cm·min-1代入传送带过炉速度,运用多重搜索算法进行搜索求值,推导出传送带的最大过炉速度vmax.
2.3.2 制程界限约束条件分析求解
运用式(9)的对数及式(8)的方程进行求解,代入点(0,25 ℃),即可求出炉前区域的常数c0,根据此c0即可计算出本温区的末温度,此末温度即为下一温区的初始温度.同理,按此顺序即可解出所有的常数c,可得电路板焊接区域中心温度的函数表达式为

(10)
最后运用多重搜索算法,通过MATLAB编程进行求解,其主要过程如下:
Step 1 取速度步长为0.1 cm·min-1,将不同的速度值代入所建立的模型进行计算,筛选出满足约束条件的各个速度值,并选取其中的速度最大值.
Step 2 将所得的速度最大值前后取±1 cm·min-1的速度范围,取步长为0.01 cm·min-1,最终得到传送带的最大过炉速度的值为vmax=83 cm·min-1.
3 峰值温度覆盖面积优化模型
3.1 模型分析
由于在焊接过程中焊接区域中心的温度超过217 ℃的时间不宜过长,峰值温度也不宜过高.理想的炉温曲线应使超过217 ℃到峰值温度所覆盖的面积最小,如图6所示.所以根据传送带过炉速度优化模型得到的电路板焊接区域中心温度的函数表达式,可以表示出温区(小温区8~9)的函数表达式,同时通过建立积分思想进行求解.假设将传送带的过炉速度和电路板第1次到达217 ℃时的时间作为积分的下限,电路板到达温度峰值时的时间作为积分的上限,列出微分方程.最后再根据限制的速度、时间和温度等相关条件,即可得到在此要求下各温区的设定温度和传送带的过炉速度,以及相应的最小阴影面积.

图6 峰值温度覆盖面积示意图Fig.6 Schematic diagram of peak temperature coverage area
3.2 模型建立
由传送带过炉速度优化模型得到的电路板焊接区域中心温度的函数表达式θ,可表示出θ4温区(小温区8~9)的函数表达式为
θ4-c4e-0.021 7t=217.
(11)
根据积分的思想,若要让阴影部分的面积最小,则需要表示出积分上限与积分下限的差值,即上限为电路板到达温度峰值时的点坐标,下限为电路板第1次到达217 ℃时的点坐标.
假设此时传送带的过炉速度为v0,电路板第1次到达217 ℃时的时间为t0,则表示的积分函数为
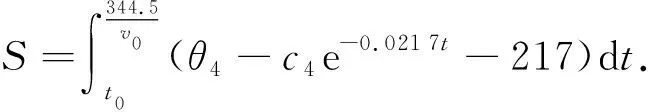
(12)
根据所给出的温区温度范围可知,各小温区设定温度可以进行±10 ℃范围内的调整.同时要满足表3中制程界限的限制条件,则其限制条件为

(13)
在式(13)的条件下对式(12)进行求解.
3.3 模型求解
不妨令xi,i∈[0,5]为各个温区的初始位移,分别为0、25、202.5、238、273.5、344.5 cm.假设炉前区域的某段温度为(1~5)温区最小值的1/2,根据多重搜索算法,运用式(10),代入点(0,25 ℃),即可求出炉前区域的常数c0,根据此c0即可计算出本温区的末温度,此末温度即为下一温区的初始温度.同理,按此顺序即可解出所有的常数c,其表达式为

(14)
对式(12)的积分进行求解,得到
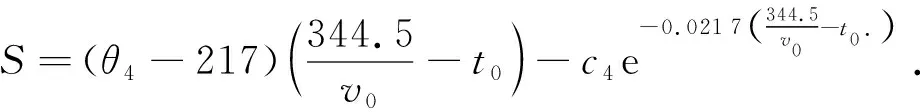
(15)
将式(11)代入式(15),可得到

(16)
根据式(13)和式(14)所求出的制程界限限制条件,结合式(16),运用多重搜索算法进行求解,可得到各温区的设定温度和传送带的过炉速度,以及相应的最小阴影面积,如表4所示.

表4 峰值温度覆盖面积优化模型结果Table 4 Peak temperature coverage area optimization model results
4 结 语
本文基于印刷电路板焊接生产问题,通过对回焊炉内焊接区域中心点的温度变化进行机理建模,根据附件中的测量数据分析电路板吸收热量的规律,确定模型中的参数,得到各温区焊接区域中心的温度.同时基于牛顿冷却定律,根据实际生产要求的制程界限,运用多重搜索算法进行搜索求解,得到了传送带的最大过炉速度.最后基于积分思想建立峰值温度覆盖面积优化模型,给出了各温区设定温度和传送带过炉速度,以及相应的最小面积.经过对所建立的微分方程模型结果进行分析,本文模型可为回焊炉电路板焊接实际生产与测试提供理论参考.

