不平衡数据的加权集成分类算法

王荣杰，代琪，赵佳亮，陈丽芳

(1. 华北理工大学 理学院 河北 唐山 063210；2. 中国石油大学(北京) 自动化系 北京 102249)

引言

不平衡数据普遍存在于现实生活中的各个领域，具有重要的研究价值。近年来，不平衡数据分类问题成为机器学习和数据挖掘领域的研究热点。由于不平衡数据的固有特征，少数类样本的分类问题远比多数类样本困难，传统分类器不能有效地表现数据的分布特征，容易将少数类样本错分[1]。针对高度不平衡数据的分类问题，国内外研究者提出了很多分类算法，取得了一定的研究成果[2]。

与单一学习算法相比，集成学习具有优秀的泛化性能和分类精度，尤其适用于不平衡数据分类。目前常以神经网络、SVM、ELM等弱分类器作为集成学习基分类器[3]。张宗堂等人[4]将随机子空间AdaBoost算法用于不平衡数据的分类问题中，有效改善了不平衡数据的分类效果；杨毅等人[5]提出一种基于SMOTE的集成学习算法，有效提升了不平衡数据的分类精度；张剑飞等[6]结合SVM提出一种数据相对平衡转换和SVM集成加权相结合的不平衡数据分类方法，有效提升了模型的分类性能；Fan X等人[7]提出双向长短时记忆卷积神经网络加权极限学习机，可以有效识别出不平衡数据集中的少数类，提高了模型的分类性能；李晗缦等人[8]综合考虑样本的分布特点，将集成超限学习机与分层交叉验证方法结合用于不平衡数据的分类，有效弥补了单一学习机的不足，提高了少数类的分类性能；陈东等人[9]结合距离融合规则提出平衡集成学习模型并结合集成学习提出动态决策算法，这两种算法都很大程度的提升了模型的泛化能力；Bhagat[10]使用二值化技术将原始数据集分解为多个二进制类的子集，针对每个二进制类子集分别应用SMOTE进行采样，获得平衡数据子集，并在这些数据集上构建随机森林分类器，实现对不平衡数据的分类；Sun[11]将不平衡数据集转换为多个平衡数据集，在这些数据集上分别构建分类器，最后以特定的集合规则将各分类器的结果进行集成得到算法的最终结果；高聪[12]在随机森林算法的基础上，将权重向量引入代价函数中，根据各基分类器分类性能进行投票集成，从而提高了分类准确率；zong[13]在传统极限学习机基础上，提出一种可以处理不平衡数据的加权极限学习机算法，该算法能够根据不同数据集分配不同的权重并保持良好的处理性能；zhang[14]提出一种基于差分进化算法优化基分类器权重的算法，该算法在不平衡数据的分类问题上具有较好表现；许玉格等[15]定义基分类器的权值矩阵更新规则和计算方法进行迭代学习，以加权极限学习机为基分类器构建集成学习算法，并将该算法应用于污水处理故障诊断问题中提高故障的识别正确率。蒋盛益等[16]提出一种特征加权聚类算法，根据聚类后簇的特征重要度量函数进行迭代计算确定权重，避免权重过度倾向于多数类，从而提升聚类算法对少数类的识别能力。陈圣灵等[17]在boosting算法的基础上，根据基分类器预测结果增大少数类样本权重的思想，提出了优化基分类器权重的FocalBoost算法。

分析以上研究成果，集成学习已成为目前处理不平衡数据的有效方法，学者们主要从2个角度对不平衡数据分类进行研究：

(1)数据集划分算法。文献[10-11]主要采用聚类、二值化等算法进行数据集划分，形成数据子集，提升了基分类器的差异性，但这些子集只能表示原始数据的一部分，不能完全体现原始数据集的整体分布特征；

(2)集成规则与策略。文献[12-17]提出了基分类器权重确定的算法和建议，从不同角度改善了集成学习效果，但大多数研究只是集中在"利用分类器的分类准确率计算分类器的权重"，仍然存在一定的主观性和随意性，影响不平衡数据的最终分类效果。

因此，该研究从2个角度入手，提出一种新的集成分类算法(Matrix-Granule Weighted Ensemble CART classification algorithm,MGWE-CART)，结合粒计算思想对数据进行预处理，利用F-范数确定矩阵粒集成权重，以CART决策树为基分类器，对不平衡数据进行集成分类。

1理论基础

1.1 集成学习

集成学习是一种整合多个弱学习机获得比单一学习机效果更好的学习模式。在分类问题、回归问题、异常点检测等问题上，集成学习算法表现出色，与传统机器学习算法相比具有更好的准确性和稳定性[18]。

集成学习算法的基分类器选择多种多样，根据不同的数据集，可以选择"同质"基分类器，也可以选择"异质"基分类器，较多研究人员更倾向于选择"同质"基分类器进行集成学习。根据各基分类器数据之间是否存在依赖关系，可以分为1类，一类是具有强依赖关系的学习算法，以boosting算法为代表；另一类是不存在依赖关系的学习算法，以随机森林为代表[19]。

Bagging算法是一种集成学习框架，每次从原始数据集中抽取一定数量的样本组成训练样本子集，使样本子集之间互不关联，bagging算法适合与常见的弱学习机相结合，生成稳定性、训练结果更好的强学习机[20]。

1.2 CART决策树

CART决策树算法也称分类回归树，采用一种二分递归分割技术，除了CART决策树中叶结点外，其余的点都具有2个子节点，CART算法生成的决策树是一个结构简单的二叉树[21]。与常见的决策树算法相比具有较高的计算速度和稳定性，与支持向量机等算法相比不需要构建非线性模型，可以根据决策树图直观地进行决策分类[22]。Park[23]提出由标量参数化的分裂准则，构建不平衡数据的对抗集，每个决策树执行不同的分裂准则，与其他集成方法相比，具有更好的表现，降低了树的数量。

在分类问题中，数据集中类别数目为m，样本属于第i类的概率为pi，则该样本的基尼系数为[24]：

(1)

样本集S的基尼系数值为：

(2)

其中，|S|表示集合S的总样本数，|Di|表示集合S中属于第i类的样本数，基尼指数表示集合S的不确定性。

如果集合S中，属性A的值等于a的所有样本所形成的子集为S1，余下的为S2，则集合S在属性A的条件下得到的基尼指数为：

(3)

基尼指数Gini(S,A)表示集合S的不确定性，样本集的不确定性也越大[25]。

2 MGWE-CART算法设计

该算法设计流程图如图1所示。

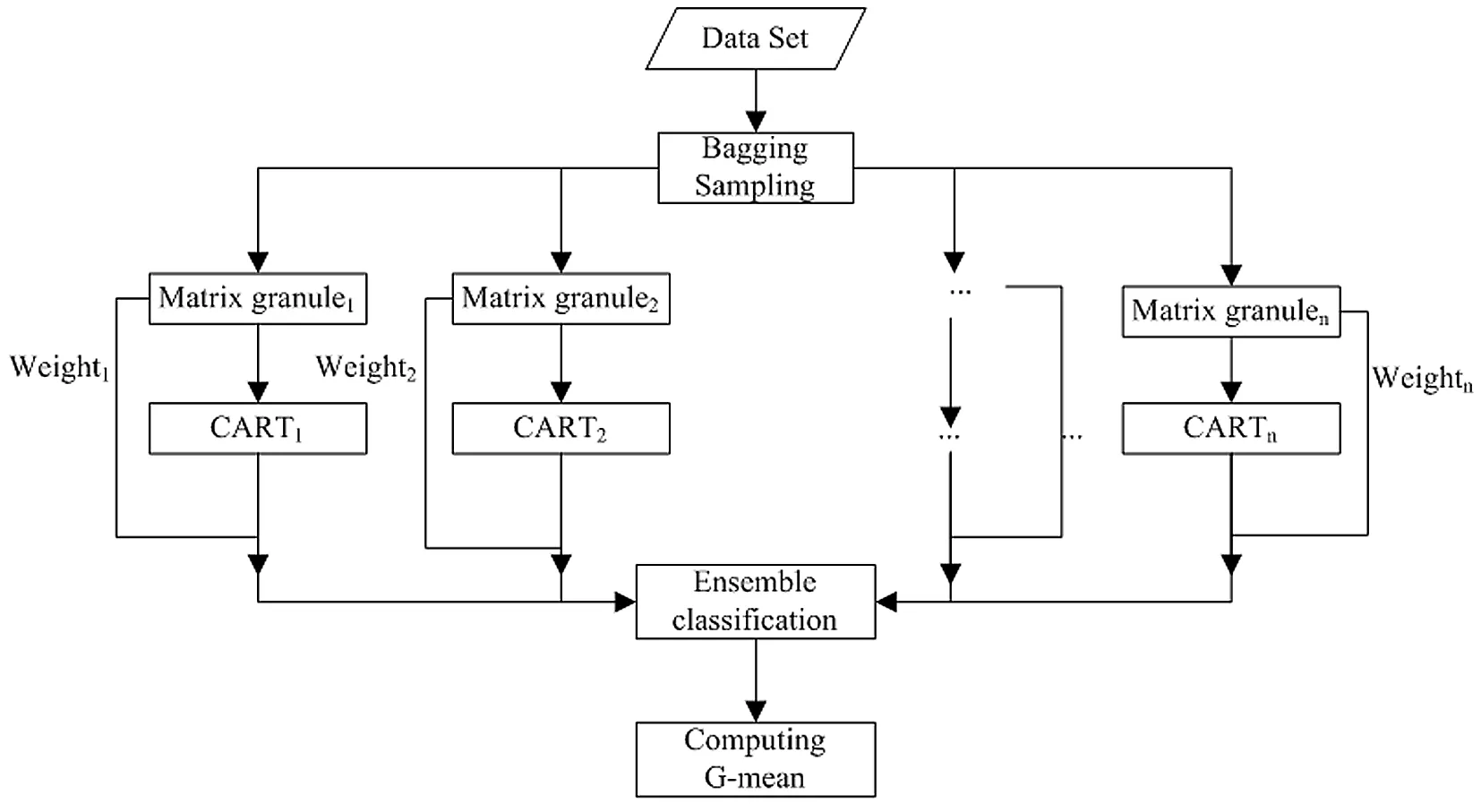
图1 集成学习分类算法流程

算法步骤如下：

Step 1：采用bagging算法对数据集进行粒化处理，形成k个粒化子集，称为数据集采样矩阵粒，用GrMk表示。

Step 2：利用基尼系数公式(2)计算原始数据及矩阵粒的基尼系数Gini(S)，删除与原始数据基尼系数相差较大的矩阵粒。

Step 3：为避免矩阵粒中数据量纲和取值范围等因素的影响，利用公式(4)对矩阵粒中的数据进行归一化处理。

(4)

Step 4：根据公式(5)求解矩阵粒与全一矩阵的差矩阵；根据公式(6)求解矩阵粒与全一矩阵之间的距离。

Dk=GrMk-Y

(5)

其中矩阵Y表示矩阵元素全为1的全一矩阵。

(6)

Step 5：分别在各矩阵粒上构建CART决策树，以G-mean值为学习机对不平衡数据的分类评价标准，公式如下：

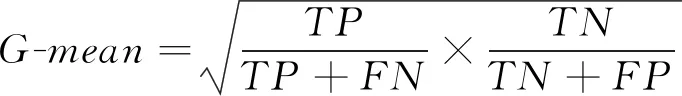
(7)

其中TP为多数类正确分类数；FN为多数类错误分类数；TN为少数类正确分类数；FP为少数类错误分类数。

Step 6：基分类器在训练集上训练完成后，以G-mean值评价学习机学习效果，舍弃G-mean小于0.5的学习机，重复Step 1；保留G-mean值大于0.5的学习机。

Step 7：根据公式(8)计算出各矩阵粒的最终权重。

(8)

Step 8：以各矩阵粒的权重为基分类器权重，将所有保留的基分类器进行加权集成，得到最终分类结果。

3算法仿真与性能分析

3.1 数据集

采用KEEL数据库(https://sci2s.ugr.es/keel/imbalanced.php)中的8组数据集进行仿真验证，实验数据集基本信息如表1。表中的不平衡比(Imbalance ratio)表示多数类与少数类的比值。

表1 数据集基本信息

3.2 算法仿真

为了验证算法的有效性和稳定性，基于Python编程，实现基于矩阵距离的CART决策树加权集成算法(Matrix-Granule Weighted Ensemble CART classification algorithm，MGWE-CART)仿真。具体算法描述如下：

(1)数据集预处理阶段

(2)Bagging采样

for (k= 1;k<=K;k±±) do

end for

(3)构建并测试基分类器

基分类器集合C=∅；

for (k= 1;k<=K;k±±) do

构建基分类器Ck；

在采样数据集Ωk上训练基分类器Ck；

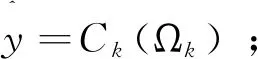
大学生职业生涯规划是一种带有预防性质的措施，虽然它主要针对的是大学生而非大学生“蚁族”，但是它恰恰能够从大学生“蚁族”产生的源头上入手，通过科学规划，分担甚至规避失业风险，从而抑制大学生“蚁族”数量的增加。这也使得大学生职业生涯规划得以实现其价值。

if (G-mean< 0.5) then

C=C∪Ck；

end if

end for

(4)计算基分类器的权重

for (k= 1;k<=K;k±±) do

计算采样数据集矩阵Ωk与全一矩阵之间的差矩阵Dk；

计算采样数据集矩阵Ωk与全一矩阵之间的距离dk；

计算基分类器Ck的权重ωk；

(5)使用基分类器在测试集上分类

构建基分类器分类矩阵Y；

for (k= 1;k<=K;k±±) do

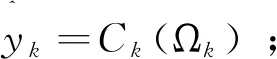
end for

(6)加权投票

构建投票矩阵V；

for (k= 1;k<=K;k±±) do

for (i= 1;i<=Ntest;i±±) do

Vi,Yki=Vi,Yki+ωK；//根据基分类器的预测结果填充投票矩阵V

end for

end for

(7)对测试集中的每条测试样本，取票数最高的类别作为最终分类结果

for (i= 1;i<=Ntest;i±±) do

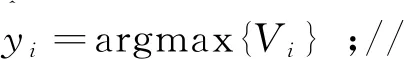
end for

(8)计算集成学习最终分类结果的G-mean值。

3.3 性能分析

由于MGWE-CART算法与投票CART算法相比优势明显，采用加权方法的ELM分类算法分类性能较差，因此直接将提出算法与采样条件相同的MGWE-SVM算法进行对比，并与文献中[26]的集成分类结果进行对比实验。文中DE-ELM与DE-WELM均是以差分进化法为集成策略，但在基分类器的选择上，DE-ELM以极限学习机为基分类器；DE-WELM则以加权极限学习机为基分类器。文中以十折交叉验证方法的方差验证算法稳定性。该算法主要采用bagging算法随机采样形成矩阵粒，每次训练均进行随机采样，随机性较强，计算100次的G-mean值标准差验证算法稳定性，并将对比文献中的方差转换为标准差。算法仿真对比结果如图2、图3所示。

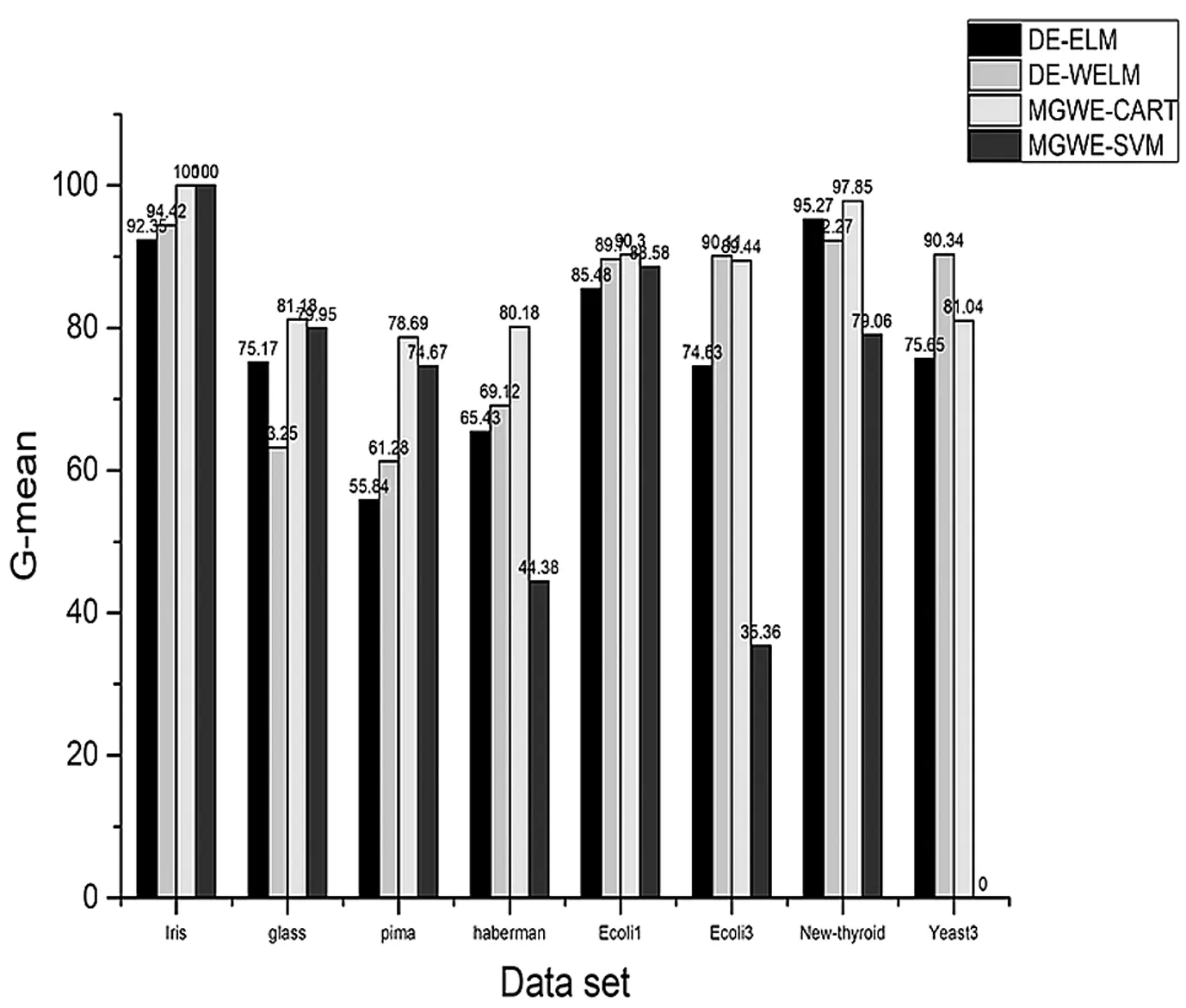
图2 算法分类结果G-mean值

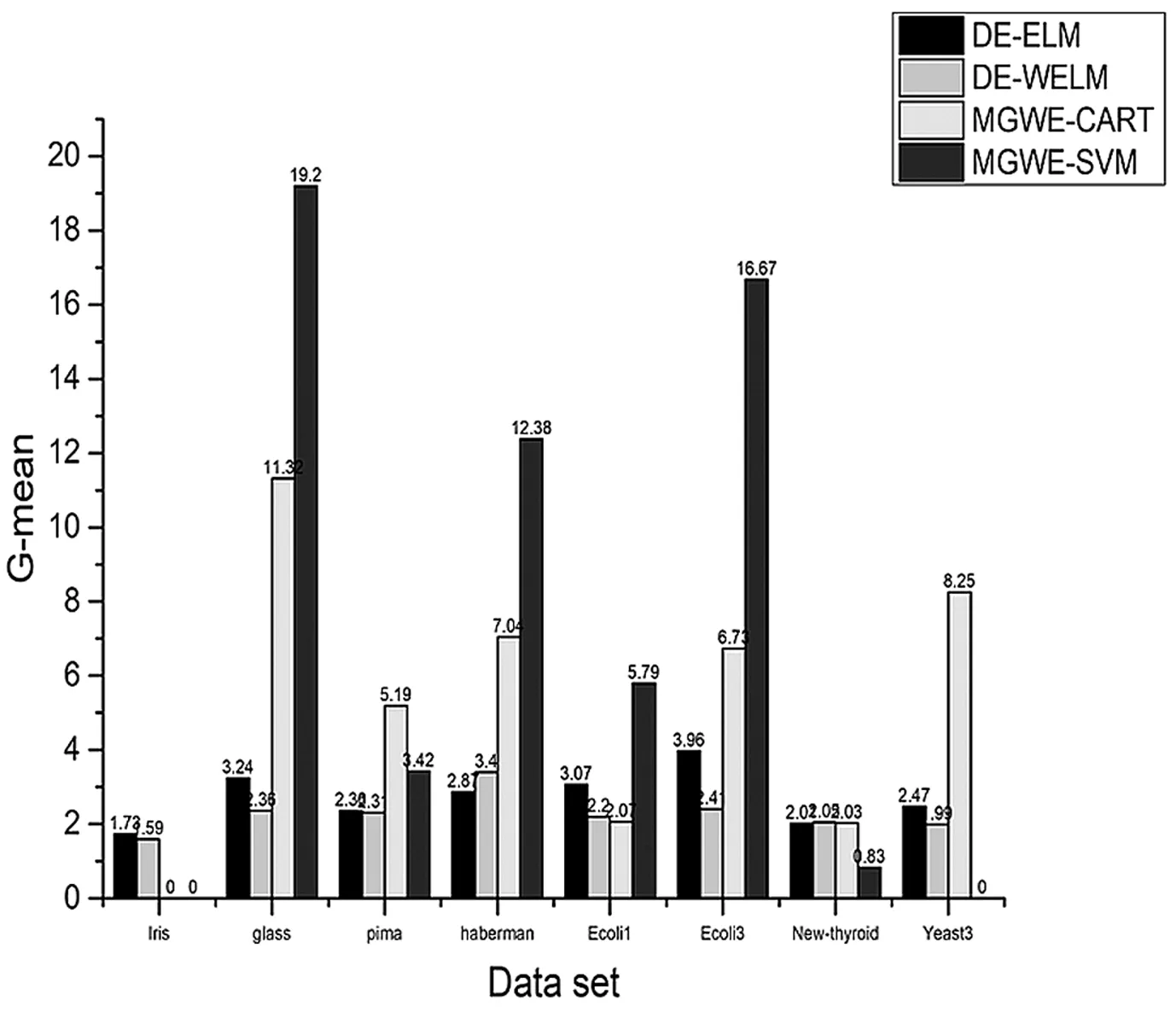
图3 算法分类结果标准差

从图2中可以看出，提出的(Matrix-Granule Weighted Ensemble CART classification algorithm,MGWE-CART)算法的G-mean值在大部分数据上明显优于其他3种算法，而ecoli3和yeast3数据集的G-mean值稍逊于其他2种算法，主要原因是这2种数据集的不平衡比较大，通过bagging采样后的矩阵粒中，少数类样本较少，学习机识别少数类样本的信息量不足，导致G-mean值偏低。

从图3中各算法的标准差可以看出，WE-CART算法在稳定性上逊色于DE-ELM和DE-WELM，而WE-SVM稳定性最差。主要原因是bagging随机采样，形成的矩阵粒随机性较强，导致稳定性较差。特别是glass数据集稳定性偏低，导致这样结果的主要原因是数据集各属性内部存在不平衡现象，分类器不能很好的学习数据信息，导致分类器稳定性较差。

最后，综合分析算法G-mean值与算法结果标准差可以得出，该种算法在不平衡比较小的数据集上，G-mean值有了较大提升，在处理高度不平衡数据时，G-mean值提升效果不明显，算法对少数类样本分类精度偏低，因此处理高度不平衡数据时，可以通过过采样、欠采样或SMOTE算法对数据进行采样，降低数据不平衡比，提升算法的分类精度和稳定性。

4结论

(1)集成学习可以充分发挥各基分类器的优势，提高算法的分类精度和稳定性。

(2)利用F-范数科学地计算bagging采样后矩阵粒的权重，可以有效地提升算法的分类精度。

(3)该算法在分类精度上明显优于其他2种算法，但稳定性较低，可以利用其他算法提升算法稳定性，该研究以矩阵距离计算方法求各基分类器的权重，使基分类器权重更加合理，避免主观因素的影响，为集成学习基分类器的权重计算提供了新的研究思路。