基于体测大数据的SFD运动好友推荐模型

李世森，张春英，吴万斌，兰思武

(1.华北理工大学 体育部，河北 唐山 063210；2.华北理工大学 理学院，河北 唐山 063210)

引言

大学生体能测试是当前检测大学生体质的重要测试之一，其反映了大学生身体体质的综合情况，是大学生学习、工作的重要保障。但是在实际中，除了规定的体育课外，学生很少进行体育运动，因此学生的身体素质和机能正在不断下降，许多学生甚至无法通过必须的体育测试[1]，且无法完成体育测试中基本的考核内容，其主要原因在于学生缺乏运动乐趣，并且不得运动要领，在课程要求的时长内难以完成课程任务，同时，学生在课外时间里，学生在进行锻炼时也同样缺少指导。体测考试会记录大量学生的体能测试成绩数据，从这些数据入手，挖掘其所蕴含的信息并以其为基础，构建推荐算法，给学生推荐一位可以互补的好友，以好友带动好友、好友间相互指导的方式，解决学生对于体育兴趣不足的问题。

作为一种常用的算法，目前已经有大量的学者对推荐算法进行研究，常见的推荐算法有基于流行度的推荐算法[2]、基于协同过滤的推荐算法[3]、基于内容的推荐方法[4]、基于用户的推荐算法[5]以及综合使用的混合方法。不同的推荐算法虽然在挑选推荐对象的方法上存在不同，在推荐对象的选取上一般都是以用户与用户间相似度作为评价标准，来对用户进行推荐。在以体测数据为基础的好友推荐问题中，单纯的以相似度作为评价的方法是不适用的，其仅仅证明用户间具有相同的兴趣。因此仅仅考虑到相似性的传统方法并不适用，仍然需要对二者间的相异进行证明，才能说明二者之间存在可以相互学习的地方。该研究结合集对分析理论，对传统的相似度计算方法进行改进，提出了一种全新的集对相似度推荐法。该方法可以综合地考虑到在推荐问题中所涉及到的确定性、不确定性、相异性的问题，与传统的推荐方法相比在涉及到不确定性的推荐问题中具有更高的准确度、合理性。

1相关工作

推荐算法是根据已有的大量数据进行分析与挖掘，根据挖掘出的信息对用户进行推荐其所喜爱的物品的算法，但是无论何种推荐算法，其内核都避不开根据同好的人进行推荐、根据喜爱的物品进行推荐、根据关键字进行推荐这3个基本条件。一般的推荐算法会存在冷启动、可拓展性差等多种问题，国内外学者已经对这些问题进行了大量的研究。

如何根据体测成绩给大学生推荐合理的能够互相学习的同伴是研究的要点。在传统的推荐算法中，所推荐的往往是用户所喜爱的物或人，但是这样的推荐方式在该研究中并不适用。若是要根据其体测成绩的相似程度来推荐一位与其能够互相学习的好友，相似程度越高则代表2个人之间可以学习的东西就越少，反之2个人差异越大，则代表可以互相学习的方面就越多。但由于是推荐交友问题，需要考虑到好友间具有相似的地方，因此，在好友推荐的问题上引入模糊的概念是该研究的研究要点。在现实生活中，一件事情往往不是非黑即白的，需要引进模糊的概念对其进行更多的处理，才能更加的贴近现实。同样的，在推荐好友的问题上，也需要引进相关的概念，才能使得推荐的结果更加具有合理性、准确性。国内外有许多学者已经对在推荐算法中引入模糊数学的方法进行了研究。文献[6]通过协同过滤法结合个人偏好对毕业生进行工作推荐，解决了零就业历史的冷启动问题，并且对偏好有较好的识别度。文献[7]研究了一种基于模糊聚类的并行推荐法，比传统的推荐方法更加合理准确，贴近现实。文献[8]针对协同过滤推荐算法多样性较低的问题，采用信息熵与用户配置信息长度2个指标来评估项目各个属性的多样性,并且对用户多样性进行模糊化处理，显著提高了个体多样性、总体多样性与新颖性。文献[9]基于模糊逻辑构建推荐相似度，与传统的相似度计算方法对比更加贴近现实且合理。集对分析[10-12]是由我国学者赵克勤于1989年提出的一种模糊数学分析法，其是在一定的问题背景下，对集对中2个集合的确定性与不确定性、相反性的相互作用所进行的一种系统和数学分析。该研究运用了集对的思想，针对在基于体测数据进行的推荐问题上需要使得差异与相似共同参与影响的问题上，利用集对联系数构建相似度，较好地解决了相关问题。

2 SFD运动好友推荐算法

2.1 算法总体设计

大学生体测推荐算法是专门根据大学生体测大数据所设计的算法，算法流程如图1。在该研究中引入了集对分析的概念对传统的相似度进行改造。在推荐过程中首先需要计算出2个对象之间的相似度，不确定度以及相异度，再根据集对分析理论计算出集对推荐度rec(A,B),最后以集对推荐度来筛选合适的推荐对象并进行推荐。

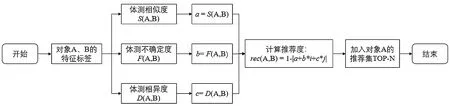
图1 大学生体测算法流程

2.2 数据预处理

在进行推荐算法的设计前，为了计算2个对象之间的体测推荐度，需要根据《国家体质标准》对大学生体测项目进行评分，将学生的体测项目数据百分制化，并且对学生身体状况分类：爆发型、耐力型、柔韧型、力量型，不同类别分数由学生体测项目成绩根据不同权重计算所得，然后通过阈值分级，确定各类别强、中、弱学生群体，最后需要对文字性的运动特征进行拟值，给出定义：{“强”：1，“中”：2，“弱”：3}。

假设存在对象A和B，将其运动特征表示成特征向量，即A=，B=,A与B特征之间的差异可由|ak-bk|表示，k∈{1,2,3,4}，

|ak-bk|=0，表示A与B具有相似度；

|ak-bk|=1，表示A与B具有不确定度；

|ak-bk|=2，表示A与B具有相异度。

该研究将在以上所描述的背景下，对体测相似度、相异度、不确定度进行设计。

2.3 集对推荐度

与传统的相似度计算推荐算法不同，需要考虑用户与用户间的相似度，用户与用户之间的差异度，以及用户与用户间的不确定因素。因此在推荐算法的相似度计算中引入集对的概念，并存在以下定义：

rel(A,B)=a+b*i+c*j

(1)

其中，rel(A,B)表示A和B之间的关联度，rel∈[-1,1]，rel越大说明相似度越高，反之相异度越低。a表示A与B之间的体测相似度，即a=S(A,B)；b表示A与B之间的体测不确定度，即b=D(A,B)；c表示A和B之间的体测相异度，即c=F(A,B)，并满足a+b+c=1。i为不确定度标记，j为相异度标记，在运算时，i与j同时作为系数参加运算，并规定j恒取值-1，i在[-1,1]区间视情况取值。集对推荐度是在关联度rel基础上进行变形，综合性考虑了相似、差异、不确定三者因素，避免因相似度或相异度过大导致推荐度高的错误情况，采取如下定义：

rec(A,B)=1-|a+b*i+c*j|

(2)

rec(A,B)表示A和B之间的集对推荐度，rec∈[0,1]，rec越趋于0，越不容易被推荐；越趋于1，则越容易被推荐。

2.3.1 体测相似度

相似度是2个对象之间相似程度的一种数值度量，是个性化推荐系统中重要的参考指标，传统的相似度是根据用户对项目的评分以及推荐利用相关公式对相似度进行计算。而该研究的体测相似度的计算方法与传统的方法不同，其是指通过获取学生体测数据，对数据分析处理，以提取描述学生的运动特征，通过一定的方法比较不同学生间的特征值来计算相似性。设在推荐系统中存在对象A、B，则推荐对象A、B存在以下相似度：

(3)

其中，S(A,B)为对象A与B之间的体测相似度，n是特征属性种类总和，ak和bk分别表示2个对象的特征值。通过一定的规则，将学生的成绩进行不同层次的划分，当2个学生的体育成绩层级相等时，则认为其具备一定的相似性，即存在N(ak=bk)是2个对象具有相同特征值的特征个数。

2.3.2体测相异度

相异度是形容2个对象之间差异程度的一种数值度量，在根据体能测试成绩的推荐问题上，仅仅根据相似度进行推荐往往是不合理的，若被推荐的双方仅存在相似度，则代表着双方可以相互学习的知识很少，因此双方需要存在一定的相异度。只有存在相异的双方，才有互相学习的可能性。设推荐系统中存在具有相异度的2个对象A、B，则推荐对象A、B存在以下相异度：

(4)

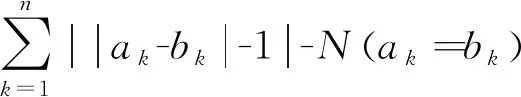
2.3.3体测不确定度

若推荐系统中存在对象A和B，当A与B之间存在一方的体育成绩为中等，另一方的成绩为强或弱时，不能以此判断双方的差距是否真的能够大到足以教导对方的程度，因此存在不确定性。在集对理论中，相似度、相异度和不确定度三者总和为1，即a+b+c=1，因此,存在对于推荐对象A、B存在以下不确定度：

(4)

2.3.4联系度i的确定

推荐系统中的对象A与B所对应的集对推荐度中，其所对应的差异不确定系数i的取值是一个需要确定的重点。当i的取值越趋近1时，2个对象之间的相似度越高，因此，利用余弦相似度，提出了一种利用计算取值法的i值确定方法，其存在以下定义：

(5)

其中s为对象A，B的余弦相似度，公式如下：

(6)

d为对象A，B的余弦相异度，在一定条件下，余弦相异度可以由余弦相似度变换而来。采用以下公式对相似度进行变换：

d=e-s

(7)

d表示2个对象之间的相异度，s表示2个对象之间的相似度，当s取值越大时，d的取值越小，i也越趋近于1；反之，i越远离1。

2.3.5 Top-N推荐集的计算及好友推荐

Top-N推荐算法是根据一定的规则对数据进行排序，并从排序列表中选取出最大或最小的N个数据进行推荐。针对不同的社会环境可制定不同的规则对推荐集中的数据进行筛选，基于大学校园学生群体进行研究，在进行好友推荐的同时需考虑多方面的因素，根据得到的用户集对推荐度集合，计算用户与被推荐用户推荐度的平均值作为阈值r，将大于阈值的推荐度存储到用户的Top-N推荐集中，如图2所示：

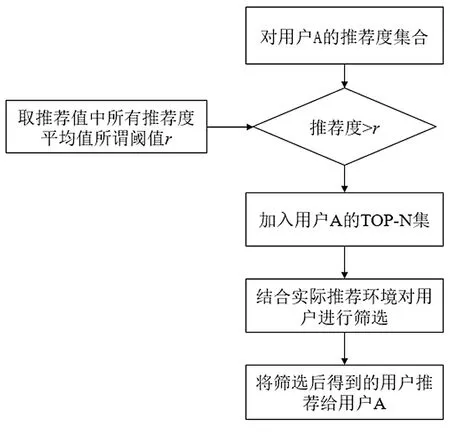
图2 Top-N推荐集的确定及好友推荐

由于在好友推荐的过程中，不仅需要考虑用户与用户两者的推荐度，还存在一些实际上的问题需要考虑，就如用户的班级、性别、生活区域的距离等，推荐时根据用户需求进行筛选。

3实验

选用数据取自某高校大学生体测成绩，数据真实可靠，且只保留体测成绩部分，姓名、学号等身份识别信息均已删除。学生体测成绩如表1、表2所示：

表1 男生部分体测数据

表2 女生部分体测数据

参照《国家体质标准》计算表1、表2学生体测成绩，如表3、表4所示：

表3 男生部分体测成绩/分

表4 女生部分体测成绩/分

结合实际情况给出体测项目对于特征的权重系数[13]，根据权重计算学生的4大特征分数，如表5所示：

表5 男、女生部分特征分数/分

根据数据分布给定阈值分级后的学生标签如表6所示：

表6 男、女生部分特征标签

以编号为10001的学生为实验对象，根据推荐算法计算得到其他学生与其的推荐度如表7所示：

表7 编号10001学生与其他学生集对推荐度

由表7计算得到的集对推荐度，可得到与编号10001学生最为匹配的部分学生，对原体测数据分析可发现，推荐的学生与实验对象之间同时兼顾相似性和相异性，符合该研究提出的推荐原则。运用于现实生活中还需要考虑实际因素，在推荐度较高的学生中，用户可根据性别、学院、年级、距离等因素进行主观筛选，从而获得与自己最为匹配的运动好友。

4结论

(1)提出基于集对理论的好友推荐模型，在相似度、相异度、不确定度公式上进行了大量的创新，运用余弦相似度计算方法及其变换确定了联系度i的取值，最终得到用户之间的推荐度。实验结果证明，所设计的推荐方法更具有针对性和互补性，推荐的用户质量性得到提高。

(2)由于特征属性种类和特征分级级数比较少，导致用户之间的差异程度较为不明显，对差异程度较大的用户具有更好的效果。故在今后的研究中，将会加入更多的特征属性，比如用户性别、用户年级等个人信息，并且对公式进行进一步改良，在保证准确率和合理性的情况下进一步提高推荐度。