基于气固两相流磨粒的刀具钝化研究*

赵雪峰，李 辉，杨 勇，秦 浩

(贵州大学机械工程学院，贵阳 550025)

0 引言

在刀具的生产过程中，未经钝化的刀具在刃区表面存在微观缺陷。为了改善刀具刃口的局部宏观和微观几何形状，提高刀具质量，创建具有更好稳定性的切削刃，减少切削刃磨损，延长刀具使用寿命，在刀具投入使用之前需要对刀具进行钝化处理。然而在对刀具进行钝化处理的过程中，刀具表面质量得以改善的同时，刀具的刃口形貌也随之发生改变[1]。目前，传统的钝化方法有立式旋转钝化法、电解法、磨粒水射流法、研磨法、磁力钝化法等。Uhlmann E[2-3]使用分散固体磨粒进行钝化实验，探究钝化过程中各钝化参数对刃口钝圆半径的影响规律。Priarone P C[4]研究了分散磨粒钝化过程中磨粒种类以及钝化时间对刀具钝化的影响。计时鸣等[5]提出采用使用气固液三相磨粒流抛光工件的磨粒流加工方法，研究了最适宜的磨粒流入射角。曾一凡等[6]提出一种超声振动磨粒流加工方法，研究了不同抛光力作用下的抛光效果。

本文提出采用气固两相流磨粒对刀具进行钝化，研究刀具正反转比例，主轴转速对刀具形状因子的影响规律。基于Jonnson理论以及能量守恒原理建立气固两相流磨粒钝化方法下硬质合金立铣刀非对称刃口形成的数学模型。

1 刀具刃口钝化

1.1 刀具刃口钝化方法

基于气固两相流磨粒的钝化方法如图1所示，磨粒桶底部有网筛，气流经网筛进入磨粒桶使得磨粒发生流态化运动，刀具在流态化磨粒中进行两级行星运动。由于刀具与磨粒之间存在相对运动，固体磨粒会不断地对刀具刃口进行冲击，使得刀具刃口材料得以去除，从而实现钝化的效果。两级行星运动简图如图2所示，刀具绕自身轴O3进行自转，轴O3绕轴O2进行一级公转运动，轴O2绕轴O1进行二级公转运动。

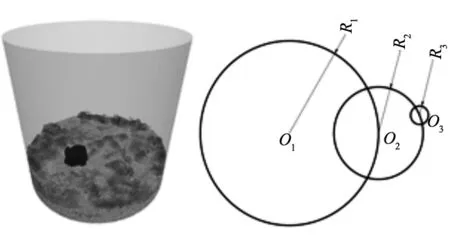
图1 刀具钝化方法 图2 刀具运动轨迹

刀具运动轨迹的数学模型为：

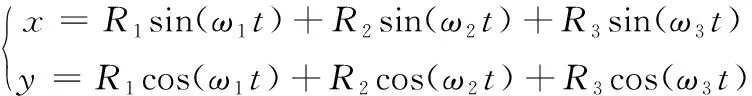
(1)

式中，R1为刀具绕中心轴转动半径；R2为刀具公转半径；R3为刀具自转半径；ω1为绕中心轴转动速度；ω2为公转转动速度；ω3为自转转动速度；t为钝化时间。

1.2 刀具非对称刃口

此数学模型采用Denkena B等[7]提出使用前刀面钝化值Sγ与后刀面钝化值Sα的比值(形状因子K)来表示刃口形貌,如图3所示。

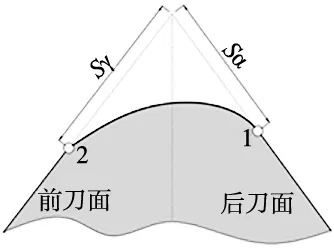
图3 形状因子表征法

为了使数学模型更加真实地反应实际钝化情况，采用形貌测绘仪器先测量出未经钝化的刀具刃口形状，由检测结果可得到所需要的未经钝化刀具的刃口有关参数L1(前刀面切点至理想刀尖点的距离)；L2(后刀面切点至理想刀尖点的距离)和刀尖角β。如图4所示，在直角坐标系中将L1所在直线看作X轴，理想刀尖点为坐标原点建立坐标系。通过几何计算可以得到前后刀面相切圆的半径r1；r2以及相应的圆心坐标。

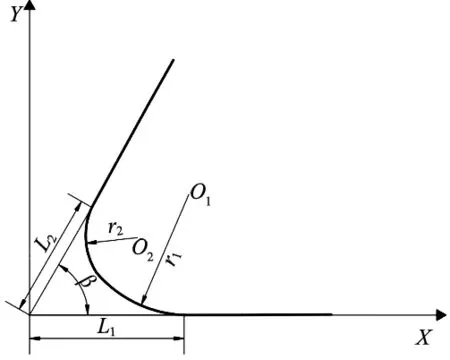
图4 坐标系的建立

2 刀具非对称刃口建模

罗刚等[8]的钝化试验表明，刀具在钝化时刃口处的磨损不仅与刀具旋转速度有关，还与刀具旋转方向相关，转速越快，刀具刃口材料磨损越快。旋转方向和刀具切向一致时，刀具前刀面更容易钝化成瀑布型刃口，钝化后前刀面的粗糙度大大提升；旋转方向相反时，后刀面更容易钝化成瀑布型刃口，钝化后的后刀面粗糙度得到很大改善。刀具正转时，法向刃口累计能量主要集中在刀具前刀面；刀具反转时，法向刃口累计能量主要集中在刀具后刀面[9]。在本文的刃口建模过程中考虑刃口钝化的复杂性，建模过程中将钝化时刀具的正反转分开计算。图5为刀具钝化前后的刃口形貌变化。

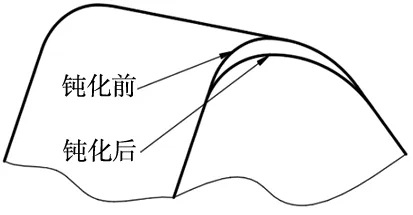
图5 刃口形貌变化

2.1 单颗磨粒冲击刃口材料的去除体积

在气固两相流磨粒对刀具进行钝化的过程中，由于磨粒流的运动状态及其复杂，刀具刃口形貌的尺寸变化达到微米级。因此本文在刃口形貌建模过程中做了以下合理假设：磨粒桶内所有磨粒目数相同，形状视为规则的球体(磨粒的球形度为1)。

单颗磨粒对刀具刃口进行冲击时，使用能量守恒原理来获得其对刀具刃口材料的去除能量，即单颗磨粒冲击前的动能与冲击后的动能之差全部转化为刀具刃口的变形能量。直径为da，密度为ρa，质量为ma的磨粒，对刀具刃口进行冲击。由于刀具的线速度与磨粒速度相比大的多。在冲击时以刀具的线速度在前后刀面的法向分量为冲击速度。刀具在正转钝化与反转钝化的过程中，冲击速度分别由刀具的前后角所决定，如图6所示，刀具正转时冲击速度v冲=v线cosγ，其中γ为刀具的前角。如图7所示，刀具反转时冲击速度v冲=v线sinα，其中α为刀具的后角。

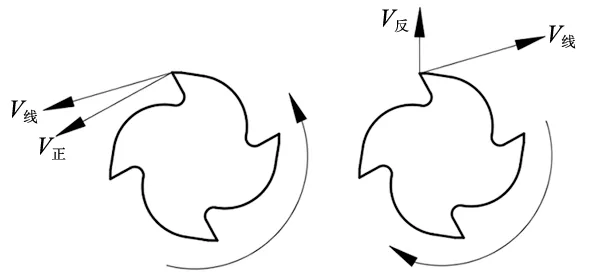
图6 刀具正转 图7 刀具反转

单颗磨粒在冲击时压入刃口表面的深度为h，如图8所示。

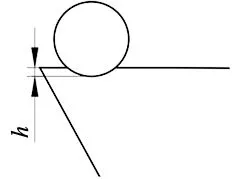
图8 单颗磨粒冲击深度

单颗磨粒冲击前的动能Ei和冲击后的动能Er如式(2)、式(3)所示：

Ei=0.5mav冲2

(2)

Er=0.5ma(v冲ep)2

(3)

式中，ep为磨粒的回弹系数。由Jonnson理论[10],如式(4)所示，回弹系数与冲击速度，磨粒的大小，密度以及刀具材料的力学性能有关。

(4)

式中，py为临界接触应力。E*为磨粒与刀具材料的等效弹性模量，其值如式(5)所示：

(5)

式中，va为磨粒泊松比；vw为刀具材料的泊松比；Ea为磨粒的弹性模量，Ew为刀具材料的弹性模量。

磨粒冲击刃口表面的冲击力为F，如式(6)所示，由于磨粒回弹，此冲击力在冲击深度h上所做的功近似为一弹性力做功。

W=0.5Fh

(6)

其中，F由刀具材料的布氏硬度HW以及磨粒与刃口表面的接触面积S共同决定。如式(7)所示：

F=S×HW

(7)

式中，磨粒与刀具刃口的接触面积是磨粒冲击刀具刃口表面所形成凹坑的表面积，这个凹坑是一个球缺，如式(8)所示，接触面积为：

S=πdah

(8)

基于能量守恒原理，由动能定理可得W=Ei-Er，结合式(2)～式(8)可求得h表达式为：

(9)

因此，可得单颗磨粒冲击刃口材料的去除体积，如式(10)所示：

(10)

2.2 多磨粒冲击刃口材料的去除体积

由单颗磨粒冲击刃口材料的去除体积求多磨粒冲击刃口材料的总体积V总，根据正转钝化时间内的磨粒冲击次数(N正)以及反转钝化时间内的磨粒冲击次数(N反)，即可获得刀具材料的去除总体积。式(1)中给定的刀具刃口运动轨迹是关于钝化时间t的函数，在正转钝化时间T正，以及反转钝化时间T反内，刀具的运动轨迹长度如式(11)、式(12)所示：

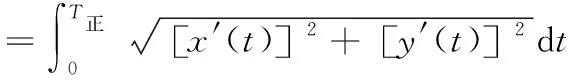
(11)

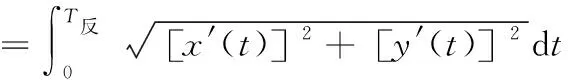
(12)

正反转钝化时间内，刀具在磨粒桶内所掠过的体积V正，V反微分形式如式(13)、式(14)所示：

dV正=LlcdS正

(13)

dV反=LlcdS反

(14)

其中，L和lc分别为参与钝化的刀刃长度和宽度。则在正反转钝化时间内磨粒冲击次数如式(15)、式(16)所示。

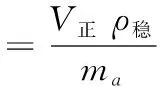
(15)

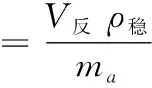
(16)

在式(15)、式(16)中，ρ稳为磨粒桶内磨粒达到相对稳态时的单位体积数量。如图9所示。

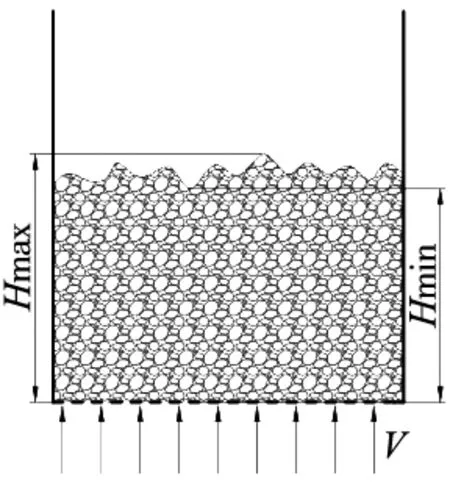
图9 磨粒平均高度

在底面积为S桶的磨粒桶中，倒入总质量为M的磨粒，磨粒桶底部吹入速度为v的空气，在磨粒达到相对稳定状态时磨粒的最大高度为Hmax,最低高度为Hmin,最大高度与最低高度通过测量可得。磨粒达到相对稳态时的平均高度H平,如式(17)所示：

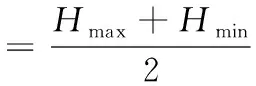
(17)

因此，磨粒达到相对稳态时的单位体积数量可求，如式(18)所示：

(18)

综上所述，在正反转钝化时间内，多磨粒冲击刃口材料的去除体积如式(19)所示：

(19)

2.3 非对称刃口数学模型

刀具钝化过程中刃口材料的去除为单磨料的法向冲击使得刃口表面形成凹坑，在多磨粒的累积冲击作用下最终形成刃口形貌。因为在钝化过程中刀具前刀面和后刀面所受的冲击力不同且不均匀，所以钝化后刃口部分应为曲线弧形。如图10所示，把钝化后的刃口简化为两个标准的圆弧，即前刀面钝圆与后刀面钝圆，分别在刀具正转钝化与反转钝化的过程中形成。两圆弧的切点即正反转冲击力法向相重合的点O，图中直线OO1′所在直线为钝化过程中刃口形貌形成的特征方向，此特征方向与磨粒冲击力有关，因为在磨粒冲击过程中这条直线上任意一点的冲击力方向皆与这条直线平行，所以使用这个特征方向来表示刃口形貌的形成是合理的。

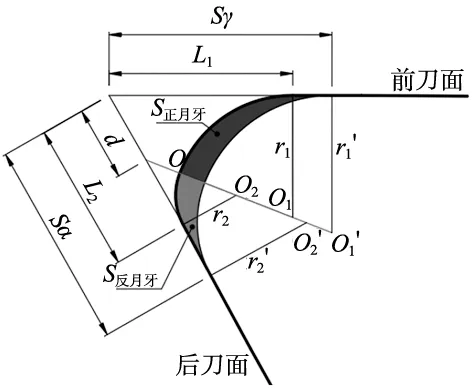
图10 钝化后刃口形貌

由几何关系可得：

(20)

其中，d为特征方向所在直线与后刀面所在直线的交点至刀尖点的距离，θ1，θ2分别为前后刀面钝圆所对扇形的顶角。综上所述，从几何关系出发，钝化总去除体积如式(21)所示：

(21)

由式(19)、式(20)联立即可求得钝化后的前后刀面钝化值Sγ和Sα。钝化后的形状因子K，如式(22)所示：

(22)

3 结果分析

在同等风速条件下，根据主轴转速(800 r/min，1000 r/min，1200 r/min)和主轴正反转比例(1:3，1:1，3:1)设计二因素三水平正交实验。采用奥地利Alicona公司研发生产的全自动三维光学刀具测量仪IF-EdgeMaster 检测刀具非对称刃口半径。

根据上述数学建模所计算的钝化后形状因子的理论及实际值如表1所示。钝化后形状因子的理论值与实验值的最大误差为18.4%，最小误差为0.04%。

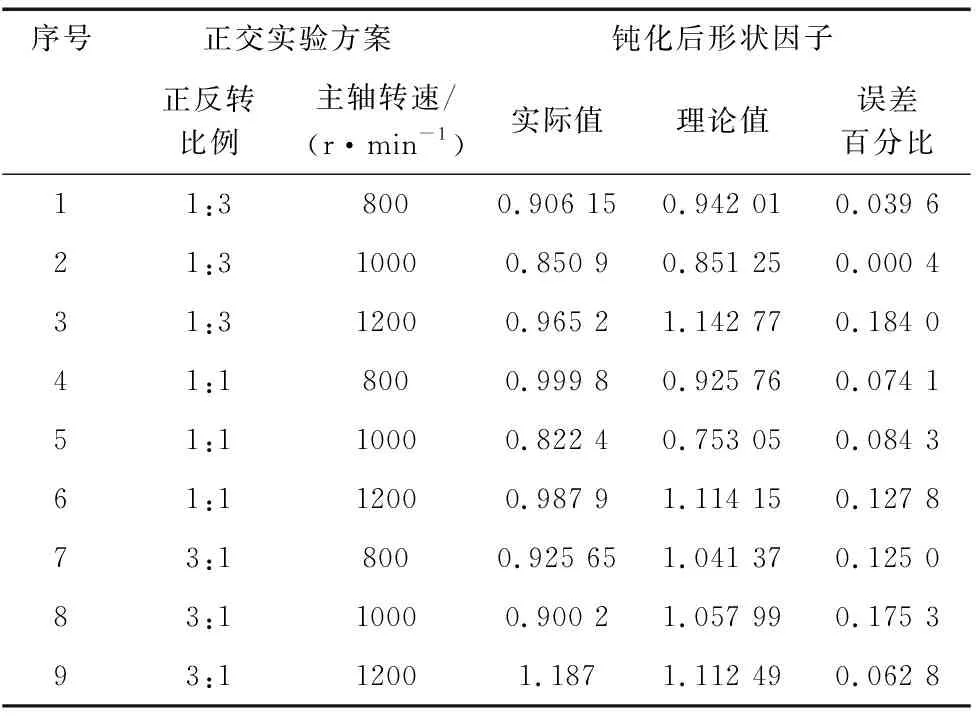
表1 正交实验方案及形状因子实验值与理论值

刀具刃口钝化参数对形状因子影响规律的理论值和实验值如图11所示。

(a)理论值 (b) 实验值 图11 实验值与理论值的对比

由图11可知，由于第三组实验(正反转比为1：3，主轴转速为1200 r/min)误差最大，理论值与实验值在此处的重合度较低，但总体上钝化后形状因子实验值与理论值的变化趋势是相近的，实验值与理论值都随主轴转速的增加呈现先减小后增大的趋势，随正反转比例的增大呈现逐渐增大的趋势，因此本文所建立的非对称刃口形成数学模型是较准确的。误差的存在主要是因为：理论建模过程中把磨粒视为了标准的球体且在钝化过程中没有考虑磨粒与磨粒之间的相互作用，在实际钝化中磨粒的并非完全规则的球体，且磨粒与磨粒之间存在相互作用；使用能量守恒定律时把磨粒冲击前后的能量损失全部转化成了冲击过程中磨粒对刃口所做的功，这一能量损失在实际钝化中还有一部分转化为了热能。

4 结论

本文提出基于气固两相流磨粒的刀具钝化方法，建立了气固两相流磨粒钝化过程中非对称刃口形成的数学模型，通过正交实验，对比理论值与实际值验证了该数学模型的准确性。

(1)基于磨粒磨损理论以及动能守恒定理，建立了在气固两相流磨粒钝化过程中刀具非对称刃口形成的数学模型。

(2)钝化后形状因子的理论值与实际值的最大误差为18.4%，最小误差为0.04%。

(3)形状因子实验值与理论值的变化趋势是相近的，实验值与理论值都随主轴转速的增加呈现先减小后增大的趋势；随正反转比例的增大呈现逐渐增大的趋势。