多卷积神经网络融合的滚动轴承故障识别方法
□ 郭双全
上海电气集团股份有限公司 中央研究院 上海 200070
1 研究背景
滚动轴承是风电机组、汽轮机、电动机、机床等工业旋转类设备的重要零部件。滚动轴承故障,易造成较大的停机损失和影响。因此,及时识别或预警滚动轴承的故障状态,对于保障设备安全运行和高效运维有重要意义。
在工程实践中,为保障大型设备可靠运行,往往配备在线监测系统,对振动、电气、压力等关键参数进行动态高频采样监测。采用传统故障状态诊断方法时,通过时域分析、频域分析、时频分析等进行特征提取[1-3],通过支持向量机、神经网络、随机森林等方法进行故障状态识别[4]。随着深度学习技术在视觉和语音识别方面的快速发展,部分学者开始研究卷积神经网络在轴承故障诊断方面的应用[5]。李恒等[6]提出短时傅里叶变换和卷积神经网络相结合的轴承故障诊断方法。韩树发等[7]提出一种改进的深度迁移学习算法——联合领域自适应算法,与卷积神经网络相结合,进行多工况故障诊断,效果优于单一卷积神经网络。
虽然采用卷积神经网络可以在一定程度上实现对轴承故障状态下复杂时频特征的提取,但是模型层数和模型参数的确定需要多次尝试和较多的经验,还未形成可靠的方法,往往训练的模型泛化性能不足。集成学习算法可以通过对多个弱学习器的融合,显著提高模型的泛化性能[8]。由此,笔者针对振动信号时频谱图,即短时傅里叶变换谱的数据结构特点,设计三个不同的卷积神经网络模型,通过全连接神经网络对这三个不同的卷积神经网络进行融合,采用常用的引导聚集集成学习方法训练融合模型,实现对滚动轴承故障状态的智能识别。通过试验将融合模型与单一卷积神经网络模型对比,从模型测试结果准确性、训练过程稳定性及效率等方面进行对比分析。
2 多卷积神经网络融合设计
滚动轴承的振动信号是典型的非平稳信号,一般采用时频分析作为振动信号处理的基本方法。常见的时频分析方法包括短时傅里叶变换、小波变换、S变换、希尔伯特-黄变换等。时频分析得到的时频谱图反映出滚动轴承振动信号在不同时间与频率维度下的能量强度,可以多角度展现振动信号的细节变化,有效描述振动信号细微变化的滚动轴承故障特征。
2.1 预处理
笔者采用短时傅里叶变换方法对滚动轴承振动信号进行预处理,得到时频谱图。短时傅里叶变换方法采用固定长度的窗函数对振动信号进行截取,对截取的振动信号进行傅里叶变换计算,得到某时刻的局部频谱。连续在时间轴上移动窗函数,截取振动信号进行傅里叶变换,最终得到不同时刻的局部频谱的集合,结果为关于时刻t与频率f的二维函数。短时傅里叶变换方法理论公式为:

(1)
式中:τ为时刻;x(τ)为时刻τ的振动信号;ω(τ-t)为时刻τ与时刻t时间差对应的窗函数。
在实际信号处理中,振动信号一般为离散的高频采样序列,需要采用短时傅里叶变换离散计算公式:
(2)
式中:m为离散采样时刻顺序;n为离散频率点顺序;s[k]为第k个离散采样时刻信号;γ(k-m)为离散采样时刻顺序k与m差值对应的离散窗函数;L为离散窗函数长度。
输出的离散结果S[m,n]为二维时频谱图,如图1所示。假设短时傅里叶变换输出矩阵大小为Ms×Ns,时间维度Ms为56,频率维度Ns为501。时频谱图反映了信号在不同时刻和频率的幅值大小,既是时域和频域特性的综合体现,也可以看作是信号在Ms个不同时刻对应的频率分布情况或信号在Ns个不同频率对应的时间变化趋势。
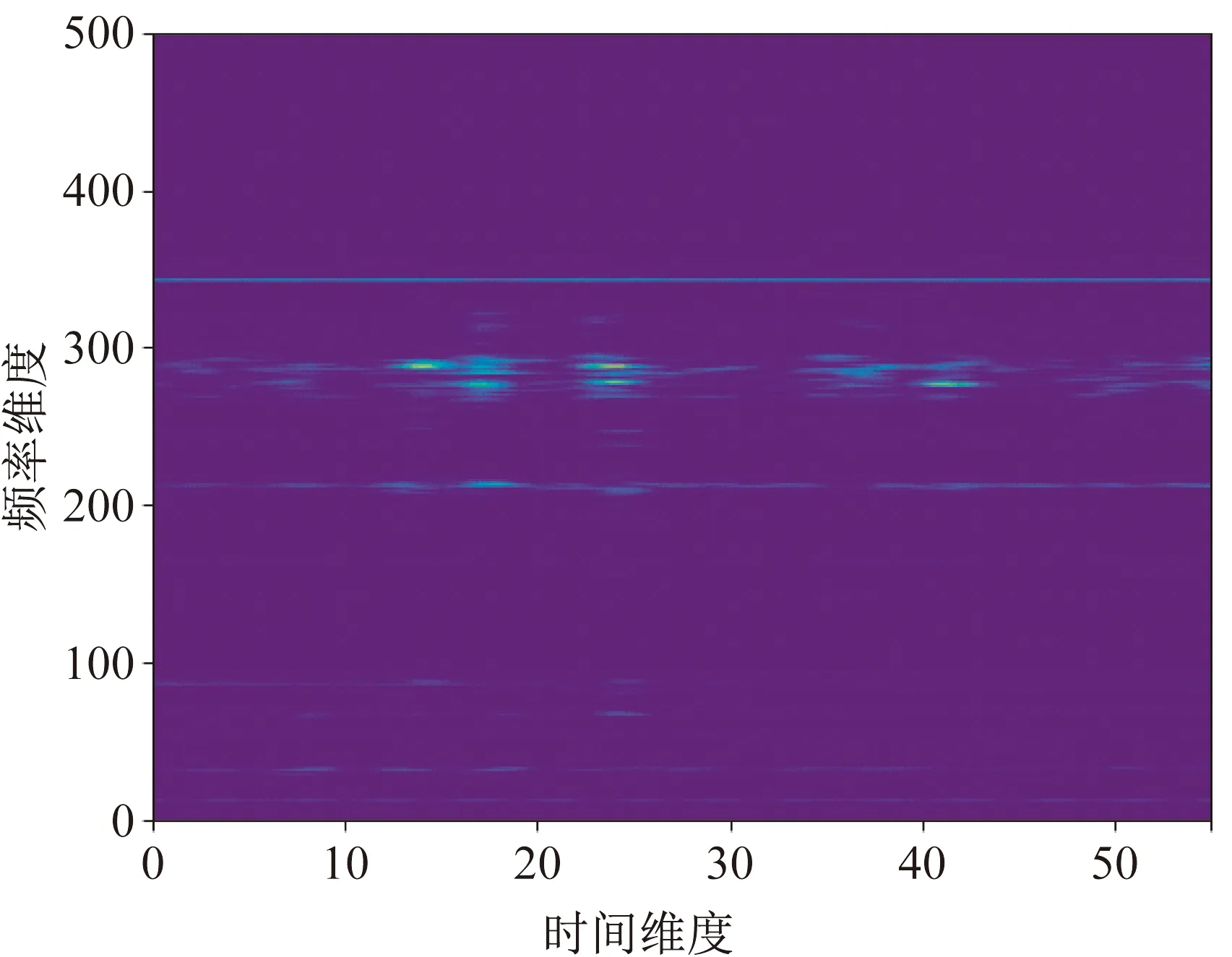
图1 二维时频谱图
2.2 卷积神经网络
卷积神经网络一般由输入层、卷积层、池化层、过渡层、全连接层、输出层组成,通过多层特征提取层能自适应从输入信息中充分挖掘抽象特征,具有较强的泛化能力和判别能力,同时具有对移动、缩放、扭曲不变性的特点。卷积神经网络可以将振动信号预处理得到的时频谱图作为输入层,进行自动特征提取识别时频特性,实现状态识别。
卷积层主要通过将输入特征图与多个卷积核进行卷积计算,加上偏置项,经过激活函数,输出新的特征图。假设卷积层的输入特征图包含N个通道,输出特征图包含M个通道,则有[9]:
(3)
式中:Cq为卷积层输出特征图第q个通道矩阵;Xp为输入特征图第p个通道矩阵;Wpq为输入特征图第p个通道矩阵在进行卷积计算得到输出特征图第q个通道矩阵时采用的卷积核权重矩阵;bq为偏置项;F为激活函数。
池化层主要对输入特征图进行计算变换,包括最大值池化、平均值池化、随机值池化等,输出尺寸较小的特征图,同时保持特征基本尺度不变。池化层一般只改变特征图的尺寸大小,不做权值更新。
过渡层一般作为卷积层或池化层与全连接层连接的过渡层,将输入特征图展开为一维特征向量,不做实际计算。
全连接层对输入的一维特征向量进行加权求和偏置,通过激活函数,输出新的一维特征向量,计算式为:
(4)
式中:yv为全连接层输出特征向量对应值;xu为全连接层输入特征向量对应值;U为全连接层输入特征向量总数;J为全连接层输出特征向量总数;wuv为对应权重因数;bv为偏置项;θ为激活函数。
为设计出合适的卷积神经网络结构,需综合考虑输入图像大小、各层类型、卷积核大小与数量等多种因素。一般采用常用的深度学习网络,结合数据特点和专业经验进行修改,通过改变各层网络参数或适当增加网络层数,建立适合根据滚动轴承短时傅里叶变换时频谱图进行故障诊断的网络模型。
LeNet-5是一种用于手写体字符识别的非常高效的卷积神经网络[10]。这一卷积神经网络总共包括七层:三层卷积层、两层池化层、两层全连接层,网络将3像素×32像素×32像素手写体图片输入数据转换为10节点输出向量,0~9代表模型识别的数字。笔者在LeNet-5网络的基础上,将短时傅里叶变换输出矩阵呈现的时频谱图作为输入,根据时频谱图在时域和频域不同的尺度大小,以及不同的卷积操作形式,改变网络参数,设计典型的卷积神经网络模型,将时频谱图输入数据转换为对应的滚动轴承故障状态的节点输出。
为了充分应用卷积神经网络综合提取滚动轴承振动信号预处理得到的时频谱图特征,笔者考虑设计三个不同的卷积神经网络:二维卷积神经网络、一维时域卷积神经网络、一维频域卷积神经网络。
将短时傅里叶变换Ms×Ns输出矩阵呈现的时频谱图作为单通道二维图像,构建二维卷积神经网络,对应二维的卷积核和池化核。二维卷积神经网络能够利用卷积特性在频域和时域上同时提取特征。二维卷积神经网络如图2所示,包括输入层、三个卷积层、三个池化层、过渡层、三个全连接层、输出层。其中,输入层为时频谱图的简化表示,各个卷积层和池化层的输出为对应的特征图,过渡层用于将池化层的输出特征图平铺展开为一维特征向量,与全连接层的神经元一一映射。图2中各标识数字为网络设计参数,如“输入层1通道501×56”表示输入层为单通道,Ns为501,Ms为56;“卷积层15×3核”表示卷积层采用对应大小的二维卷积核;“特征图3通道164×54”表示经过卷积层计算后输出的特征图包括三个通道,每个通道的大小为164×54;“隐含神经元400个”表示与全连接层相连的隐含神经元的数量。输出层的节点数对应轴承故障的状态数。

图2 二维卷积神经网络
可以将短时傅里叶变换输出矩阵呈现的时频谱图看作按频率维度划分的对应Ns个频率通道的时间变化子图的集合,从而构建一维时域卷积神经网络,对应一维的卷积核和池化核。一维时域卷积神经网络侧重利用卷积特性在时域上提取特征。一维时域卷积神经网络如图3所示,包括输入层、三个卷积层、两个池化层、过渡层、三个全连接层、输出层。其中,输入层是时频谱图按频率维度进行通道划分后的简化表示,各个卷积层和池化层的输出为对应的特征图。
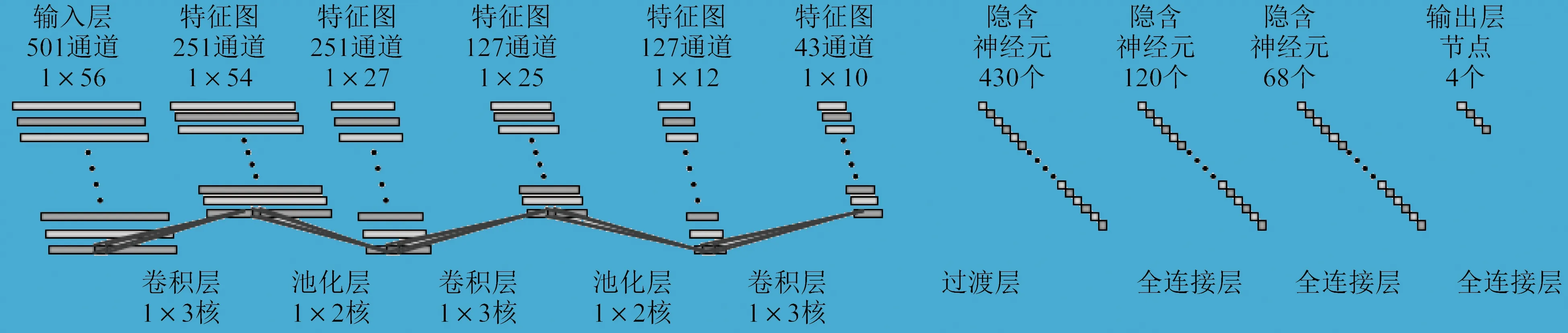
图3 一维时域卷积神经网络
可以将短时傅里叶变换输出矩阵呈现的时频谱图看作按时间维度划分的对应Ms个时间通道的一维频率分布子图的集合,从而构建一维频域卷积神经网络,对应一维的卷积核和池化核。一维频域卷积神经网络侧重利用卷积特性在频域上提取特征。一维频域卷积神经网络如图4所示,包括输入层、三个卷积层、两个池化层、过渡层、三个全连接层、输出层。其中,输入层是时频谱图按时间维度进行通道划分后的简化表示,各个卷积层和池化层的输出为对应的特征图。
图4 一维频域卷积神经网络
3 集成学习
集成学习时,训练若干个个体学习器,通过一定的结合策略,形成一个强学习器。根据个体学习器之间依赖关系的不同,集成方法一般分为引导聚集算法和提升算法两种。笔者采用引导聚集算法对设计的三个不同卷积神经网络进行集成,形成融合模型。集成学习如图5所示。

图5 集成学习
引导聚集算法首先通过对样本数为N的训练集T进行有放回的随机采样,构建出与训练集大小相同的采样集T1、T2、T3,然后利用采样集分别训练二维卷积神经网络模型、一维时域卷积神经网络模型、一维频域卷积神经网络模型,最后对这三个卷积网络模型的输出采用结合策略集成,一般结合策略包括平均法、投票法、学习法。笔者采用学习法设计一种常规全连接神经网络进行集成,最终得到融合模型。全连接神经网络的输出即为融合模型的最终输出结果。全连接神经网络如图6所示,包括输入层、隐含层、输出层。将前述三个不同卷积神经网络模型的输出结果作为输入层,经过隐含层计算后输出最终结果,即为轴承的故障状态。

图6 全连接神经网络
4 试验分析
为验证模型训练效果,采用滚动轴承振动数据集,经过处理得到某滚动轴承在正常、外圈故障、内圈故障、滚动体故障时,受到不同转速和负载情况的振动信号样本472条,每条样本信号的采样频率为12 000 Hz,采样时长为1 s。滚动轴承正常、外圈故障、内圈故障、滚动体故障四种状态的样本数依次为a、b、c、d。
采用前述步骤,将样本划分为训练集和测试集,进行对比训练,比较融合模型和单一卷积神经网络模型在训练精度和效率上的差异。训练策略为通过集成学习对融合模型进行训练,包括对二维卷积神经网络模型、一维时域卷积神经网络模型、一维频域卷积神经网络模型进行训练,以及对全连接神经网络训练K次。将K设为10、30、50,逐渐增加集成学习的训练次数,并在每次集成学习训练后利用测试集对融合模型和单一卷积神经网络模型进行验证。验证准确率随集成学习训练次数的变化曲线如图7所示。
以验证准确率99%为基准,由图7可以看出,融合模型比三个单一卷积神经网络模型更快收敛达到基准,并且训练过程更为稳定,而单一卷积神经网络训练过程中存在一定的震荡。另一方面,不同K值对应的融合模型收敛次数并无明显变化,表明采用全连接神经网络进行融合具有较好的泛化能力,在实际应用中选取较小的K即可达到提高准确率的效果。

图7 验证准确率随集成学习训练次数变化曲线
为进一步验证融合模型对验证准确率的改善效果,对固定K值的三种情况分别进行三次重复试验,共计九次,统计各次试验中融合模型和各单一卷积神经网络模型分别达到验证准确率99%所需的训练次数,具体见表1。由表1数据可以看出,融合模型所需训练次数相比单一卷积神经网络模型所需训练次数明显减少,具有较好的稳定性。

表1 验证准确率达到99%试验结果
5 结束语
笔者提出的多卷积神经网络融合的滚动轴承故障识别方法,集成了多种不同结构类型的卷积神经网络,提高了对滚动轴承振动信号时频特征的提取能力。试验结果表明,与单一卷积神经网络模型相比,通过集成学习得到的多卷积神经网络融合模型能够通过较少的训练次数达到相同的验证准确率,有效识别滚动轴承故障状态,并且训练过程稳定性和泛化性较好。后续可以通过优化网络结构参数和改进集成学习策略,不断提高模型对滚动轴承故障的识别精度。

