KTV最优点歌策略问题算法分析与研究

刁 航，金昕怡

（1.东北林业大学信息与计算机工程学院，黑龙江 哈尔滨 150040；2.东北林业大学机电工程学院，黑龙江 哈尔滨 150040）

日常生活中，在时间有限、选择有限的情况下，经常需要选择最优策略使利益最大化。所谓最优策略，指在相同约束条件下能尽最大可能满足要求的策略。KTV唱歌是一种常见的娱乐项目，点歌时在价格固定的前提下会有唱歌时长有限、点歌选择有限、歌曲时长不同等问题，就会出现最优点歌策略，即在相同时间下点唱曲目尽可能多、离开KTV时间尽可能晚。关于这类问题的解法多种多样，其中贪心算法、动态规划算法最为常用。贪心算法是一种经过改进后的分级处理方法，其特点是一步一步进行，根据某个优化测度，每一步都要保证能获得局部最优解[1]。贪心算法需要根据题意先行确定一个量度标准，而大多数量度标准下所得的解不一定为问题最优解[2]。动态规划算法的基本思想是将待求解问题分解成若干子问题，并利用问题的最优子结构性质，以自底向上的方式递归地从子问题的最优解逐步构造出整个问题的最优解[3]。本文分别采用这两种算法处理问题并进行对比。

1 KT V最优点歌策略问题描述

一般来说，KTV不会在“时间到”的时候鲁莽地把你正在唱的歌曲“切掉”，而是会等它放完。例如，在还有15 s的时候再唱一首2 min的歌曲，则实际上多唱了105 s。但是融合了多首歌曲的《劲歌金曲》《情歌王》等歌曲时长超过10 min，如果唱这种歌曲，相当于多唱了超过600 s。假设唱歌时间还剩t秒，接下来只能唱n首，不考虑切歌，并在时间结束之前再唱一个《劲歌金曲》或者《情歌王》，使得唱的总曲目数量尽量多，在此前提下尽量晚离开KTV。通常情况下，设定n（n≤50），t（t≤109）和每首曲目的时长（不超过3 min），得到唱的总曲目数量及总时长，保证n+1首曲目的总时长严格大于t。

2 贪心算法和动态规划算法具体描述

2.1 题目算法分析

在题目中，曲目数量与时长是给定的，因此在处理时要将n首曲目抽象成歌曲数组song[i]（0＜i≤n），下标i代表第i首曲目，数组song[i]存储的是第i首歌的时长，把n首歌的取舍用向量[x1x2x3…xi]来表示，其中每一个xi只能有0，1两种取值，当xi=1时，表示第i首歌被点唱；xi=0时则表示该首歌不被点唱。因此本问题就可以抽象化为求取约束条件为0≤i≤n，在song[i]数组的基础上对选歌策略进行分析[4]。本文选用贪心算法与动态规划算法分别进行分析与解决。

2.2 贪心算法

贪心算法是在对问题求解时总是做出在当前看来是最好的选择。也就是说，这种思想并不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解。在利用贪心算法求解KTV最优点歌策略时，可选择的贪心策略量度如下：时长优先。以时长为量度标准，先唱时长最长的歌曲，尽量保证不会出现时长上的浪费。曲目优先。以演唱曲目数量为量度标准，先唱时长较短的歌曲，保证最终演唱曲目数量最多。

由于曲目数量、演唱时长都是约束条件，在实际生活需求与题目要求中，一般根据尽可能多唱曲目为前提，因此面临两种量度策略，选取曲目优先策略，目标函数为约束条件为song[i]xi≤t，xi∈{0,1}，0≤i≤n，即先对歌曲数组song[i]按照歌曲时长升序排列，在剩余t时间内，当未达到时间上限时，继续按顺序演唱下一首，直到加上第k首歌的时长后超出了t的时间范围，取前k-1首歌曲作为点歌曲目。这种方法虽然可以得到一组可行的解，但并不是最优解，容易造成时间上的浪费。为了满足离开时间尽量晚的约束条件，本文在上述算法思想的基础上进行优化。考虑在出现time[k-1]+time[k]＞t，即加入第k首歌曲导致时长超出上限时，执行以下两种优化算法策略。第一种，因为歌曲是按照时间升序排序的，所以第2首到第k首的总时长一定大于第1首到第k-1首，所以向后选取更新选择的歌曲，以此来达到唱歌时间尽量长的要求。当第一种策略不成立时，执行第二种策略，保证前k-2首歌曲的选择不变，考虑用后面歌曲替代第k-1首，观察是否比原第k-1首更能在时间限制内满足离开时间尽量晚的要求。贪心算法核心伪代码见图1。

图1 贪心算法核心伪代码

本解法关键点在于选择了曲目数优先的策略，将歌曲按照时长进行排序，并且在排序后根据离开时间尽量晚的要求考虑替换歌曲问题，最终达到演唱时长与t相差尽量少的结果。然而在实际问题中，由于贪心算法的性质，上述两种优化后的贪心策略依然无法保证取到最优解，只能得到一个可行解，并且在本题目的限制下第一种优化策略与最优解差距最小。尤其在不考虑切歌的情况下，贪心算法往往无法取得最贴合时间长度的策略，最终得到的结果可能是选择的k-1首歌曲总时长与时间上限t还有一定距离，造成时间上的浪费，导致无法达到尽可能晚离开KTV的要求，同时在歌曲数目较多且时长相差不明显的情况下，优化算法容易导致开销增大，占据过多运算资源，所以本文提出了基于动态规划算法思想的解决方案。

2.3 动态规划算法

动态规划算法是一种自下而上的算法，往往能够给非NP问题求得一组最优解。在利用动态规划算法求解KTV问题时，可以将问题抽象成一种类似复杂化0-1背包问题的情况[5]，时长t相当于背包容量，备选歌曲相当于可选择的物品。由于有两个限制条件，即要求在所选曲目有限制的情况下唱的曲目最多，并且在限制时长为t的情况下离开时间最晚，所以设置两个数组，即dp[i][j]记录歌曲数目，time[i][j]记录演唱时长，用两层循环来进行数量与时间的动态规划。状态递推方程代码见图2。动态规划算法核心伪代码见第36页图3。

图2 状态递推方程代码

图3 动态规划算法核心伪代码

本题动态规划算法的策略是在先通过第一重循环dp[i][j]求出唱的曲目最多的情况后，在所唱曲目尽量多的前提下再使用第二重循环time[i][j]，选出离开时间尽量晚（唱歌时间尽量长）的情况，从而得到唱的曲目最多、离开时间最晚的最优解。动态规划算法可以得到题目的精确最优解，但是在时间与空间上较贪心算法更复杂，开销更大。

3 贪心算法和动态规划算法复杂度对比分析

因为题目中总时长t的取值与备选歌曲总数n的值较大，所以从时间与空间复杂度层面上来看，贪心算法更为优越。贪心算法通过将歌曲按照时长为量度进行升序排序，按顺序选取直到超出时长上限，在此基础上运用优化算法不断重新选取歌曲使总时长不断趋近限制t，因此贪心算法的时间复杂度为排序所需付出的代价，空间复杂度为歌曲数组所占空间；而动态规划问题的时间复杂度代价为两重循环，先查找演唱曲目最多的情况，然后在得出的尽量多的曲目基础上查找总时长最长的情况，最后能得到演唱曲目尽量多、离开KTV时间尽量晚的最优解，空间复杂度为dp数组与time数组的空间乘积大小[6]。两种算法复杂度对比见表1。

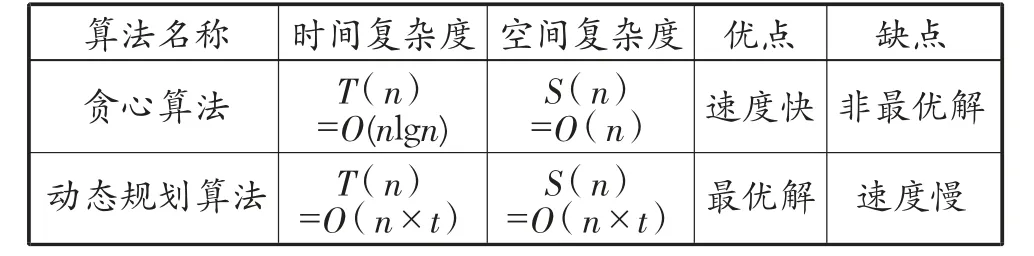
表1 两种算法复杂度对比表

在解决实际问题的过程中，贪心算法往往无法得到最优解，只能得到一组可行解，对结果精确度要求不高时可以使用；动态规划算法虽然复杂度更高，但是结果更为精准，是更好的选择[7-9]。

4 结论

本文通过利用贪心算法与动态规划算法从两种思想角度分析并解决KTV最优点歌策略问题。其中，贪心算法的时间空间复杂度较低，但只能得到一组可行解，无法求得最优解；动态规划算法采用两重循环，虽然时间与空间复杂度较贪心算法更高，但是在实际问题解决的过程中显然是更科学有效的算法。因此，获得KTV最优点歌策略问题最优解，使用动态规划算法是更好的选择，但是具体问题要具体分析，从实际需求的角度出发来选择最恰当的算法，以求高效、实用、快捷。