六西格玛理论在氯碱用离子交换膜二次溶胀率试验中的应用

李晓，杨淼坤，孙芙荣，刘康，张江山，冯威，张永明

(1.含氟功能膜材料国家重点实验室，山东 桓台 256401；2.山东东岳高分子材料有限公司，山东 淄博 256401；3.山东华夏神舟新材料有限公司，山东 淄博 256401)

自从1962年美国杜邦公司(DuPont)的Nafion全氟磺酸离子交换膜下线[1-2]，离子膜法制碱逐渐淘汰传统方法。2020年，中国离子膜法烧碱产量达到3 643万t[3]。经过数十年的刻苦研发，我国的氯碱膜制造加工技术经历了从无到有、从有到优的发展过程。在国产氯碱膜制造加工技术飞速进步的过程中，也遇到了许多棘手问题，其中比较突出的是膜产品在包装后二次溶胀导致膜面起皱的问题，影响着膜的感观和客户的使用体验[4]。

六西格玛理论方法是在1986年由时任摩托罗拉工程师的比尔·史密斯提出的，旨在减少产品和服务缺陷的先进管理方法。从20世纪中期开始被美国通用电气公司(GE)从一种全面质量管理方法演变为一套高度有效的企业流程设计、改善和优化的技术，并提供了一系列同等的适用于设计、生产和服务的新产品开发工具。其中尤为重要的一种工具是试验设计(DoE)，其特点是利用有限的试验建立数学模型，预测试验结果。完全析因试验设计是DoE中较为简单的一种试验设计方法，在该方法中，每个试验参数只有2个水平，这些参数可以是数值型的变量，也可以是分类型的变量[5]。王坤明等人[6]利用完全析因设计方法实现了对KDF4/AF4成型机组滤棒加工参数的优化，使滤棒得率提高约0.68%。马琳等人[7]通过完全析因试验设计方法完成了托吡酯微丸挤出滚圆制备工艺的优化，找到了最佳参数组合。马晓丽等人[8]采用完全析因设计方法在影响三丝高速CO2双边角焊缝成形参数的众多因素中找到了最主要的影响因素，并建立了数学模型。叶红玲等人[9]利用完全析因试验发明了一种全新的组合簧片式空间可展结构优化设计方法。完全析因试验设计方法在多个行业已经得到了广泛的认可和使用，然而，在氯碱离子膜领域，仍鲜见该方法的应用案例。

本文通过对氯碱离子膜采用不同浸泡液浸泡，采取加速溶胀的方法模拟存储过程中自然环境的变化对膜的影响，利用六西格玛理论中的完全析因试验设计方法，对浸泡液的成分和浓度进行了优化探索，缓解膜在存储过程中的二次溶胀现象，改善膜的表观状态。

1 试验部分

1.1 试剂与仪器

氢氧化钠(上海国药集团有限公司，粒装，质量分数≥99.9%)，碳酸氢钠(莱阳市康德化工有限公司，质量分数≥99.5%)。

电子恒温水浴锅，不锈钢浸泡槽，酒精温度计(量程0～100 ℃)，钢尺(精度1.0 mm)，壁纸刀，游标卡尺(精度0.02 mm)，分析天平(精确至0.000 1 g)。

1.2 完全析因设计

响应Y=“膜二次溶胀率”，其计算方法如下：

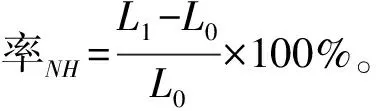
(1)

式中：L0是膜在室温下浸泡液中浸泡平衡时尺寸，L1是室温下浸泡平衡后，升温至35 ℃再冷却至室温重新浸泡平衡尺寸(该溶胀率为横、纵向溶胀率均值)。

令x1=“浸泡液溶质”，变化区间为(NaOH，NaHCO3)；x2=“浸泡液浓度”，变化区间为0.2%～2.0%(质量分数)。

利用JMP软件针对Y进行基于x1和x2的完全析因设计，中心点数1，重复次数1，得到试验设计矩阵以及响应值如表1所示。

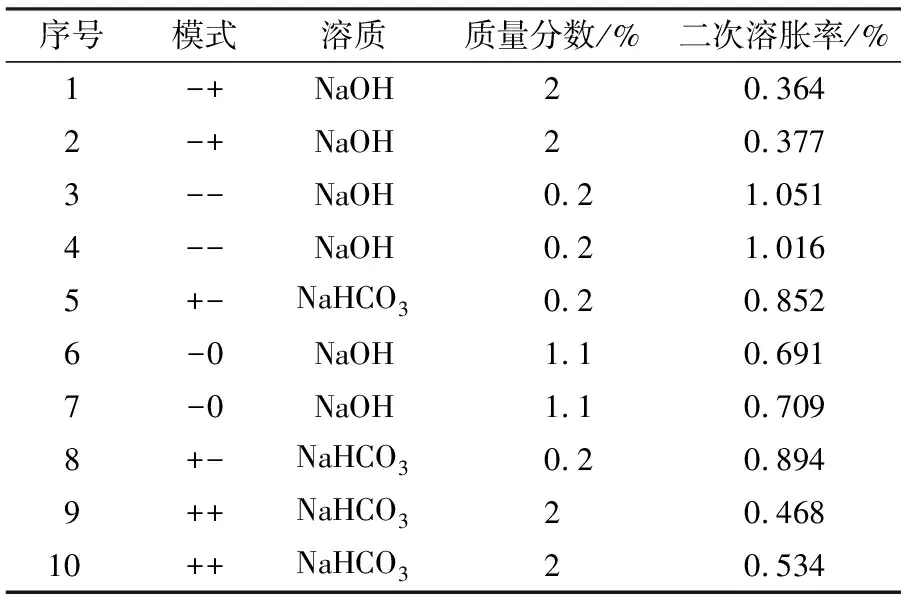
表1 JMP软件给出的完全吸因试验设计矩阵

1.3 氯碱离子膜二次溶胀率的测定

取氯碱离子膜18 cm×20 cm，浸泡在室温(16±1)℃浸泡液中3 h左右，每0.5 h测定一次横、纵向尺寸，至前后两次测定其尺寸不再变化，认为氯碱离子膜已处于平衡状态。

测定浸泡在室温平衡液中的处于平衡状态下的氯碱离子膜的横向、纵向尺寸，取平均值记为L0。

将室温下平衡后的氯碱离子膜在恒温35 ℃的纯水中浸泡3 h，每0.5 h测定一次横、纵向尺寸，3 h后将膜重新浸泡在室温(16±1)℃下的浸泡液中至平衡状态，测定其横、纵向尺寸，并将其平均值记为L1。

按照公式(1)对膜在不同浸泡液中处理后的二次溶胀率进行计算，并填表1。

2 模型建立与参数优化

模型的建立采用JMP13软件进行，对完全析因试验设计矩阵中的数据进行统计分析。预测值与实际值的拟合效果如图1所示。

图1 二次溶胀率预测值与实际值的模型拟合效果图

由图1可以看出预测值与实际值的线性拟合误差区间狭窄，说明模型预测结果与实际试验结果相近。

依据效应汇总结果对模型进行简化处理，初始效应汇总结果如表2所示。

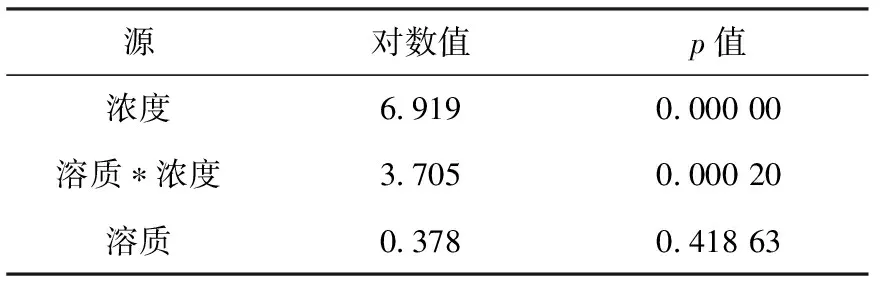
表2 模型效应汇总

表2所示p值大于0.05的参数为对响应值影响较小的参数，应当删除，即将“溶质”项删除，得到简化后的模型如表3所示。由此可以看出：对模型响应影响显著的因素有2个，即溶液的浓度和溶质*浓度的二阶交互效应。

表3 简化后的模型效应汇总

模型的残差指模型中响应的预测值与实际值的差值。对于有效模型来说，对残差的分布状态进行分析，残差需要符合“三性”，即均匀性、随机性和正态性。如图2、图3所示，响应“二次溶胀率”的残差分布随预测值和行号的变化没有明显规律，符合分布随机性与均匀性；W值为0.908 978时，对残差分布进行正态性检验，其正态性拟合优度= 0.274 0，大于0.05，说明残差分布符合正态分布。综上所述，模型的残差分布符合“三性”，模型为有效模型。

图2 预测值与残差的分布图

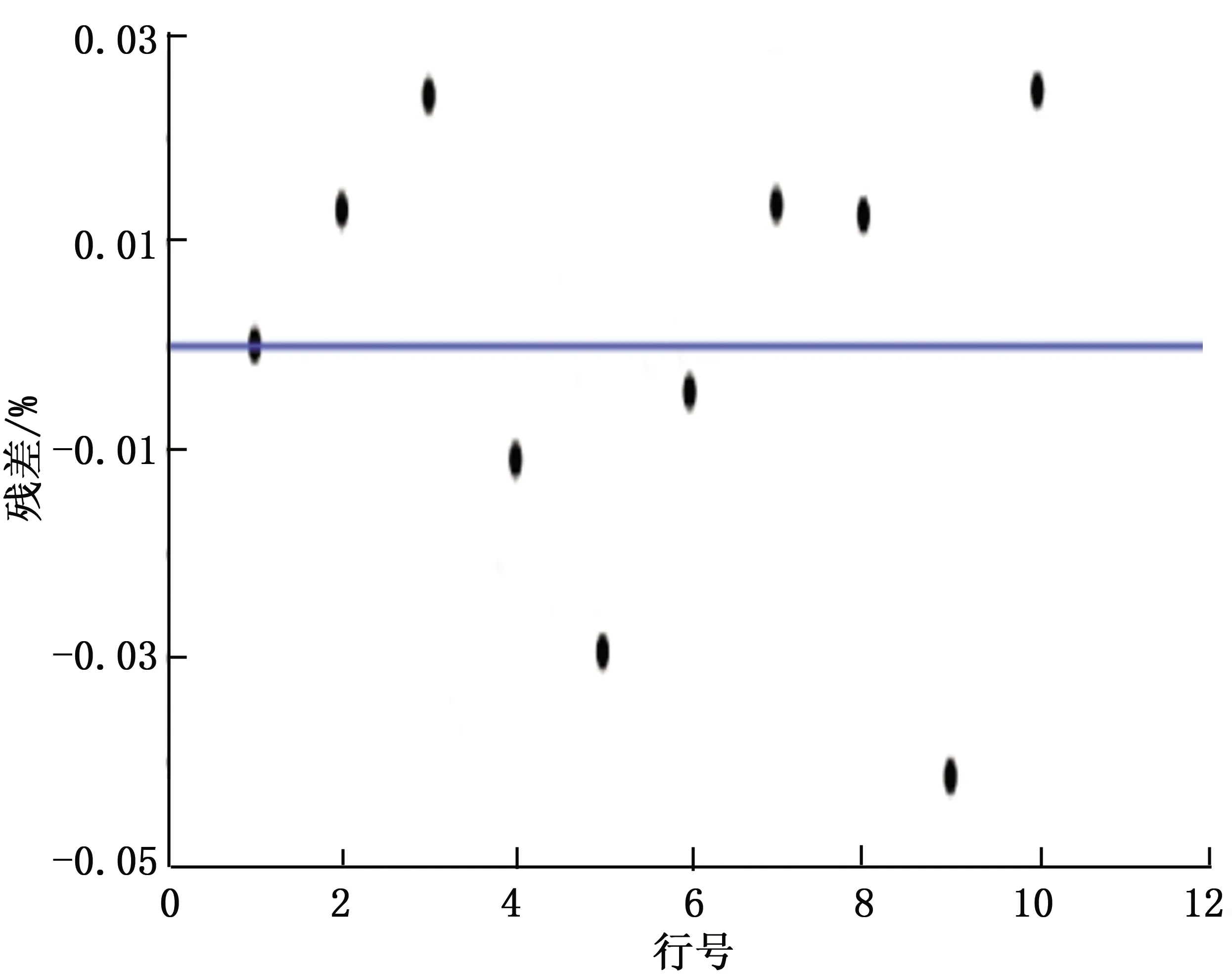
图3 行号与残差的分布图

从失拟的分析结果(如表4)来看，模型的失拟平方和为0.000 498，占总误差平方和的11.27%，纯误差平方和为0.003 919，占总误差平方和的88.73%。由此可见，模型的总误差中，由环境因素等造成的误差占比更大，而由模型拟合所造成的误差更小，说明模型的拟合效果较好。此外，由模型方差分析结果(如表5)中F比小于0.000 1也可以判断出模型拟合效果较好。

表4 模型失拟分析

表5 模型方差分析

模型参数估计值及概率值如表6所示。

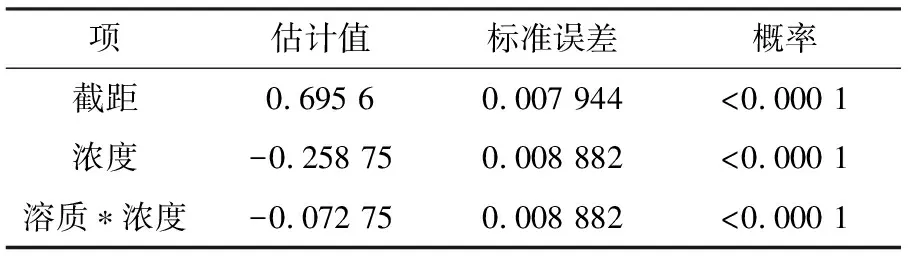
表6 模型参数估计值及概率值

由表6可知：对于模型的响应“二次溶胀率”来说，效应“浓度”和二阶交互效应“溶质*浓度”是显著影响因素，这与模型简化后效应汇总所得到的结论相符。除此之外，由表6还可以进一步得到模型响应的预测表达式如下：

二次溶胀率=

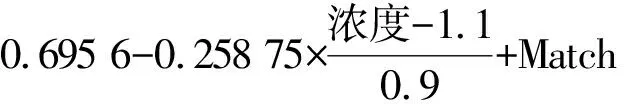
对模型的响应“二次溶胀率”进行意愿设置(如表7)，期望该数值越小越好，即可得到如图4的预测刻画器分析结果，由此可知，当溶质为NaOH，质量分数为2%时，氯碱离子膜的二次溶胀率达到最小值，其数值范围是0.329%～0.399%。从图中还可以看出，随着NaOH浓度的增大，二次溶胀率呈现逐渐减小的趋势。

模型预测刻画器响应目标值设定二次溶胀率的最大值为1.10，目标值为0.55，最小值为0.00。

模型预测刻画器及最优化参数分析如图4所示。

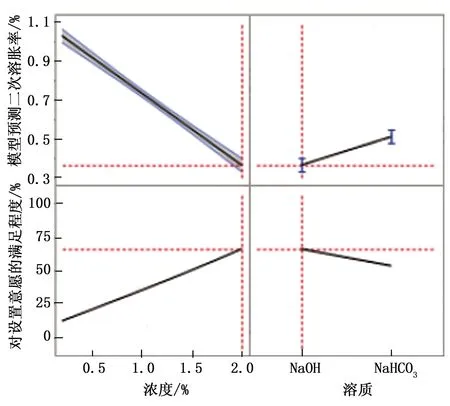
图4 模型预测刻画器及最优化参数分析

3 验证

利用上述模型对溶质为NaHCO3质量分数为1.1%时和溶质为NaOH，质量分数为0.8%时氯碱离子膜的二次溶胀率进行预测，并通过试验进行结果的验证，具体数据如表7所示。

由表7数据可以看出：真实的试验数据处在完全析因试验设计给出的数学模型预测范围之内，认为该模型预测效果较好，结果具有良好的再现性和重复性。

表7 对数学模型预测结果进行结论验证

4 结论

利用六西格玛理论和完全析因试验设计方法，通过对不同溶质(NaOH、NaHCO3)及不同质量分数(0.2%～2.0%)溶液浸泡处理后的氯碱离子膜进行加速溶胀前后横、纵向尺寸的测定，并利用JMP13软件进行建模和统计分析，得到了拟合效果良好的模型。通过预测值与实际值的对比验证，认为该数学模型可用于预测响应值“二次溶胀率”随溶质和浓度的变化情况。此外，还利用统计分析后给出的模型，得到了二次溶胀率最小的参数组合，即溶质采用NaOH，质量分数为2.0%，此时，氯碱离子膜的最小二次溶胀率范围为0.329%～0.399%。