灰土挤密桩复合地基累积变形影响因素敏感性分析

杨建周

(蒙冀铁路有限责任公司，呼和浩特 010000)

1 概述

铁路列车动力荷载循环作用下路基会产生弹性和塑性变形。在单次动力荷载作用下，路基的塑性变形在总变形中的比例很小；在循环动力荷载的作用下，塑性变形逐渐累积，最终形成永久变形，严重时会导致路基出现不均匀变形，增加轨道不平顺性，甚至会危及行车安全。对于大轴重货运铁路[1]，路基不均匀变形现象更加常见。由此可见，列车荷载循环动力作用下路基的累积塑性变形对线路的安全运营尤为关键。因此，为保证列车安全行驶，如何科学.准确地预测列车动力荷载引起的路基和地基累积变形意义重大。

目前，对循环动荷载下土体累积塑性变形的研究通常采用基于经验拟合公式的实用简化算法。Monisimith等[2]提出了Power模型，通过计算得出了软黏土的累积塑性应变与加载次数的关系，但模型中忽略了循环动应力和初始静应力的影响；LI D.Q.与SELIG等[3-5]引入土体的破坏静偏应力，并根据土体的类型和物理性质的影响对Power模型进行了修正；李进军[6]根据土层的力学指标算出静力破坏偏应力，同时计算出车辆荷载引起的动偏应力，然后利用累积应变的经验公式及分层总和法计算出地基的总沉降值；董亮[7-8]通过路基三维有限元动力模型计算和现场试验结果，基于修正的Power模型，得到高速列车长期循环荷载作用下土质路基的累积变形预测模型，并基于模型计算结果与现场激振试验结果的对比分析，对模型的可靠性进行了验证。

本文依托黄土地区某铁路灰土挤密桩复合地基加固工程，基于简化型算法，根据西北黄土地区的工程实际情况，从动力学角度出发，建立复合地基累积塑性变形预测模型，并通过该模型对灰土挤密桩复合地基累积变形影响因素进行敏感性分析，为灰土挤密桩的优化设计提供理论依据。

2 预测模型

影响土体累积塑性变形的主要因素有：动偏应力.静力破坏强度和荷载动力作用的循环次数。针对黄土地区某铁路路堑段灰土挤密桩加固路基各结构层土体的工况，基于文献[9]提到的基床表层.基床底层和挤密黄土地基预测表达式，采用分段积分方法对累积变形预测模型中各层土体的累积变形进行求和，以得到总变形。

2.1 基本表达式

列车荷载作用下，试验段基床表层.底层土体和挤密黄土的累积塑性应变[10-18]可表示为

[1+(136w-4)lgN]

(1)

εpf=1.098·(σd/σs)1.1·N0.18

(2)

式中，εpab和εpf分别为基床表层.底层土体和挤密黄土的累积应变；σd为循环动荷载引起的动偏应力；σ3为固结围压；w为含水率；σs为静破坏强度；N为振动次数。

由弹塑性力学理论可知，动偏应力σd的表达如式(3)所示。

σd={[(σx-σy)2+(σy-σz)2+(σz-σx)2+

(3)

式中，σx.σy.σz.τxy.τyz.τzx为6个动应力分量。

2.2 参数选取及计算方法

根据文献[9]中的本构模型.材料参数和运动方程等资料，建立轨道-路基-地基三维动力有限元模型。通过计算得到路基各结构层的动偏应力σd，根据已知各土层的物理力学指标计算出静破坏强度σs，取基床表面(h=0)到结构层一定深度为积分区间进行分段积分计算，得到列车长期循环动力作用下灰土挤密桩复合地基的累积塑性变形预测模型。

2.2.1 动偏应力计算

结合有限元模型和公式(3)，可以计算出土体不同深度处的动偏应力。图1为轴重200，250，300，350 kN条件下，货车以速度100 km/h开行通过灰土挤密桩复合地基段路基动偏应力沿深度方向的衰减曲线。

图1 不同轴重下路基动偏应力衰减曲线

从图1得知，在不同轴重条件下，复合地基段的动偏应力竖向分布特征类似，均沿着竖向逐渐衰减。列车轴重为200，250，300，350 kN时，基床表面的动偏应力如表1所示。

表1 基床表面动偏应力汇总

对图1中的动偏应力衰减曲线进行拟合，分析结果表明路基各结构层的动偏应力与深度之间的关系可利用幂函数来表达，其关系式如下

σd=a·hb

(4)

式中，σd为动偏应力；h为地基中某点距基床表面的竖向距离；a和b为拟合参数。

同理，以轴重250 kN.桩长6 m的工况条件为例，基于相应的有限元模型计算，得到不同桩间距和桩径条件下的动偏应力衰减曲线，拟合参数a.b取值如表2所示。

表2 动偏应衰减曲线拟合参数

根据拟合参数，可得到不同轴重条件下路基动偏应力与土体深度h的关系式，将其代入到式(1)和式(2)中，可建立路基各层土体的累积应变与其埋深之间的关系。

2.2.2 静力破坏强度计算

根据沈珠江[20]提出的有效固结应力理论，土体静破坏强度σs可表达如下

σs=2qf=

(5)

式中，σs为土体静破坏强度；qf为不排水抗剪强度；参数ccu为土的黏聚力；φcu为土的内摩擦角；K0为土的侧压力系数；γ为土体重度；h为土体深度。

其中，根据挤密黄土的室内三轴试验结果[9]，其黏聚力ccu.内摩擦角φcu与挤密黄土的含水率w及挤密系数K密切相关，取值如表3所示。

表3 不同挤密系数.含水率条件下黄土强度参数

为简化计算，本文涉及的挤密黄土静破坏强度计算中，土体的ccu和φcu值统一按表3中w=14.5%.K=0.90条件下取值，即ccu=88.11 kPa，φcu=28.39°。

2.3 累积塑性总变形预测模型

综上所述，分别对基床表层.基床底层和地基土层的累积塑性应变进行分段积分，即可得到路基累积塑性总变形预测模型，表达式如下

(6)

式中，s总为路基总累积塑性变形；sa.sb.sf分别为基床表层.底层和复合地基土层的累积塑性变形；ε1pab.ε1pf分别为基床表层.底层和地基土的累积塑性应变；h为距基床表面距离，基床表层厚度为0.7 m。

3 模型验证

为了验证所建立的累积塑性变形预测模型的可靠性，基于长期运营线路的累积变形观测数据，与预测模型计算结果进行对比验证。

从该铁路开通运营开始，对设置在某处的灰土挤密桩复合地基处理的路基工点沉降观测桩进行累积变形连续观测，观测的基本参数如表4所示。

表4 变形观测基本参数

在修建的混凝土水准标石上架设高精度水准仪进行观测，观测时间为2012年12月至2014年12月，期间，试验工点的累积沉降曲线如图2所示。

图2 观测断面累积变形曲线

由图2得知，在观测初期，累积变形曲线斜率较大，随着观测时间的推移，曲线斜率逐渐减小，曲线形态趋于平缓。观测点所在线路上以开行C80和C70型货车为主，每天约开行16对列车，每节车厢有2个转向架，每节车厢通过观测点时动荷载作用2次。

为了验证预测模型的可靠性，把观测间隔时间等效为振动次数，将预测模型中250 kN轴重货车作用下的路基累积变形曲线与观测桩的实测累积变形曲线进行对比，结果如图3所示。

图3 路基累积变形实测值与预测值对比

对比图3中路基累积变形实测值与预测值曲线，可以发现实测与预测曲线趋势较为一致：等效振动次数约10万次时，即列车运营的初期(1个月左右)，路基的累积变形量增长迅速，振动次数达到50万次时，累积变形曲线开始出现略微减缓的趋势，振动次数60万次～180万次时，累积变形曲线趋于缓慢增加，振动次数达到180万次以上后，累积变形基本趋于稳定。

验证结果表明，本文提出的累积变形预测模型式(6)很好地预测了路基累积塑性变形的发展趋势，具有较高的可靠性。

4 累积变形影响因素敏感性分析

影响灰土挤密桩复合地基累积塑性变形的外因主要有轨道平顺性.道砟厚度.轴重.车速和车辆性能等，内因主要包括桩长.桩径.桩间距和桩土模量比等因素。在外部影响因素一定的情况下，本节以桩体的几何特征等内部因素为研究对象，利用式(6)中复合地基累积变形的预测模型，并基于前文中动偏应力和静破坏强度参数选取及计算方法，分析桩长.桩径和桩间距对复合地基累积塑性变形的影响，根据正交设计试验方法，对各影响因素进行敏感性分析，确定不同因素之间的主次性。

4.1 桩长对累积变形的影响

改变桩长的本质就是改变灰土挤密桩的加固深度，改变地基沿深度方向的刚度。桩长的增加扩展了桩体的加固区域，提高了地基的整体强度，进而增强了地基的抗变形能力，降低了复合地基土体的累积塑性变形；桩长减小时规律则相反。取桩径为0.3 m，桩间距为0.8 m，分别计算在桩长为4.6.8.10 m和12 m的工况下，复合地基在轴重为250 kN.速度为100 km/h的货车荷载长期作用下的累积塑性变形，如图4所示。

图4 不同桩长条件下复合地基土体累积变形曲线

由图4得知，在不同桩长条件下，路堑段灰土挤密桩复合地基的累积塑性变形随着振次变化的规律基本一致，均随着振次的增加而增大，循环荷载作用初期累积变形增长率较大，之后变形趋于稳定。随着桩长的增加，累积变形逐渐减少，而且在桩长大于6 m之后，桩长对累积变形的影响逐渐降低，当达到10 m之后，桩长的增加对累积变形的影响非常有限，这表明，在动荷载循环作用下，灰土挤密桩复合地基的桩体存在着“临界动力桩长”，即当桩长达到“临界动力桩长”时，提高桩长很难减小其累积塑性变形。

4.2 桩径对累积变形的影响

改变桩体直径的本质就是改变桩本身影响范围，改变桩土面积置换率和桩土模量比，从整体上改变复合地基刚度的空间分布。桩径的增大扩展了桩体的加固区域，增强了地基的抗变形能力，起到了降低地基土体累积塑性变形的作用。但在实际工程中，由于成孔.成桩技术及机械使用的局限性，一味地靠增加桩径来提高地基的强度并不现实。为便于比较，取桩长为6 m.桩间距0.8 m，分别计算在桩径为0.2.0.3.0.4 m和0.5 m的工况下，复合地基在轴重为250 kN.速度为100 km/h的货车荷载长期作用下的累积塑性变形，计算结果如图5所示。

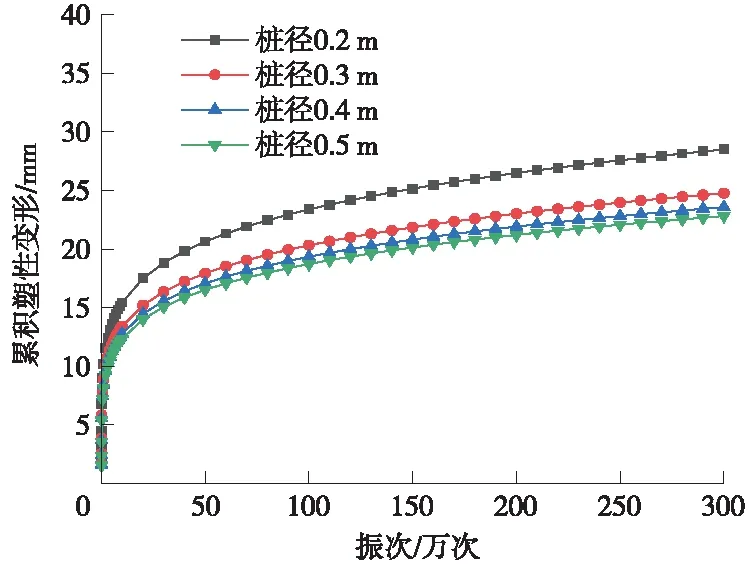
图5 不同桩径条件下复合地基土体累积变形曲线

由图5得知，在相同振动次数.不同桩径条件下，复合地基的累积塑性变形随着桩径的增大而减小，以振动300万次为例，当桩径从0.2 m增加到0.3 m时，累积变形降低了13.03%，桩径从0.3 m增至0.4 m时，累积变形降低了4.69%，桩径从0.4 m增至0.5 m时，累积变形降低了3.22%，表明随着桩径的增大，累积塑性变形降低率逐渐减小，而且这种现象随着振次的增加越来越显著。

4.3 桩间距对累积变形的影响

改变桩间距的本质就是改变桩体之间相互作用力，改变桩土面积置换率和桩间土的挤密系数。桩间距降低的同时也增加了加固区域内的桩体个数，增强了土体的抗变形能力，从而减小地基累积塑性变形。选取桩长6 m.桩径0.3 m的挤密桩，分别计算桩间距为0.6.0.8.1.0 m和1.2 m的工况下，复合地基在轴重为250 kN.速度为100 km/h的货车荷载长期作用下的累积塑性变形，如图6所示。

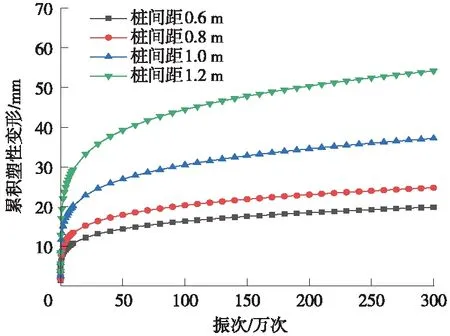
图6 不同桩间距条件下复合地基土体累积变形曲线

由图6可知，相同振动次数.不同桩间距条件下，复合地基的累积塑性变形随着桩间距的增大而增加，以振动300万次为例，桩间距从0.6 m增加到0.8 m时，累积变形增加较为缓慢，当桩间距从0.8 m增加到1.2 m时，累积变形增加速率明显增大。这表明，随着桩间距的增大，累积塑性变形增长率逐渐增大，而且这种现象随着振次的增加越来越显著。

4.4 敏感性分析

正交试验设计[21]是一种高效而经济的多因素试验设计方法，从试验的全部组合方式中挑选出有代表性的点进行试验，这些点具有均匀.可比性强的特点，具体的设计流程如图7所示。

图7 正交试验设计流程

本文在正交试验设计时，以轴重250 kN.振动300万次的累积塑性变形值作为对比计算指标，选取桩长.桩径.桩间距这3个参数作为正交试验的3个因素，每个因素选取3个水平，桩长选取0.4.0.6 m和0.8 m，桩径选取0.2.0.3 m和0.4 m，桩间距选取0.6.0.8 m和1.0 m，具体的编码如表5所示。

表5 正交试验的因素和水平

选用4因素3水平L9(34)正交表进行试验，共需进行9次，对比全面进行试验的次数34=81次，试验次数大幅减少。将3个因素放置在前3列上，最后一列空白，详细的正交试验设计方案如表6所示。

表6 灰土挤密桩加固正交设计方案

基于前文提出的累积变形预测模型，针对表6中的9种正交试验设计，分别计算出9种工况条件下路堑段灰土挤密桩复合地基的累积塑性变形，并使用正交设计助手ⅡV3.1版，得出计算结果的直观极差分析表。根据正交试验理论，极差越大表明该因素的不同水平之间的差异越大，其敏感性越强。各因素对试验结果影响分析如表7所示。

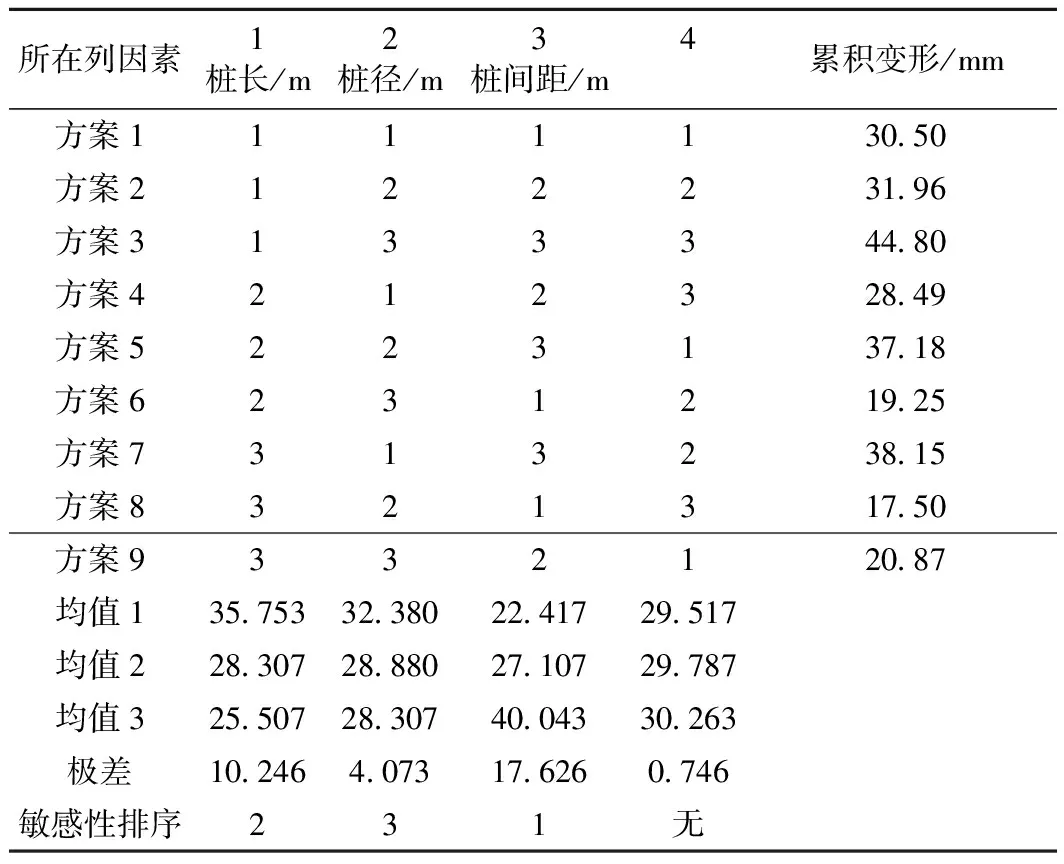
表7 累积变形试验结果的极差分析

从表7可以看出，桩间距的极差最大，桩长次之，桩径最小，这表明桩间距对复合地基的累积塑性变形最为敏感。

为了更直观地分析桩长.桩径.桩间距等因素对累积变形的影响，基于表7作出各因素对累积变形影响的效应曲线，如图8所示。

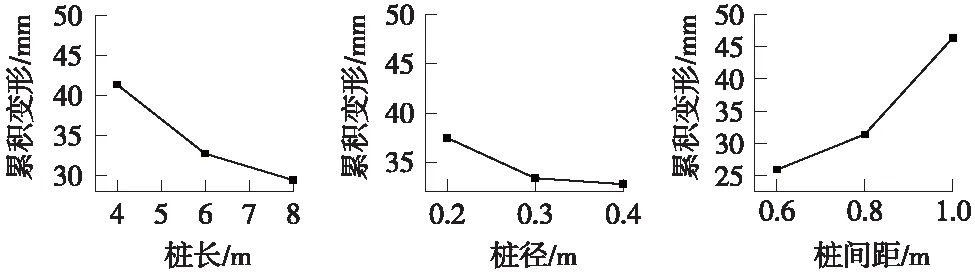
图8 各因素对地基累积变形影响的效应曲线

由图8可知，桩长从4 m增加到6 m时，路基累积塑性变形随着桩长的增加而减小，桩长从6 m增至8 m时，累积变形随桩长增加而继续减小，但降幅变缓；桩径从0.2 m增至0.3 m时，累积变形随桩径的增加微弱减小，桩径从0.3 m增至0.4 m时，累积变形变化微乎其微；桩间距从0.6 m增至0.8 m时，累积变形随桩间距增加而缓慢增大，当桩间距从0.8 m增至1.0 m时，累积变形随之急剧增大。

综上所述，灰土挤密桩的桩长.桩径和桩间距对复合地基累积塑性变形均有一定的影响，其中，桩间距对累积变形的敏感性明显高于桩长和桩径。因此，基于累积变形的考虑，对灰土挤密桩加固黄土地基进行优化设计时，在保证消除湿陷性.满足地基承载力等基本质量控制条件的前提下，为了提高工程效率和节约工程成本，可将灰土挤密桩的桩间距作为主要优化对象进行设计。

5 结论

通过对黄土地区某铁路灰土挤密桩复合地基累积塑性变形预测模型的研究，分析了灰土挤密桩几何特征参数对复合地基累积变形的影响，并对其敏感性进行了分析，主要结论如下。

(1)基于黄土地区铁路货运列车长期动力作用的工况，提出了灰土挤密桩复合地基累积塑性变形预测模型，经验证，该模型具有较好的可靠性。

(2)在动荷载循环作用下，灰土挤密桩复合地基的桩体存在着“临界动力桩长”，即当桩长达到“临界动力桩长”时，提高桩长很难降低其累积塑性变形；随着桩长和桩径的增加，地基累积变形逐渐降低，且变化率越来越小，随着桩间距的增大，累积变形逐渐增大，且变化率越来越大；上述三因素的影响随着振次的增加越来越明显。

(3)灰土挤密桩桩间距对累积变形的敏感性明显高于桩长和桩径，因此，进行灰土挤密桩优化设计时，建议将桩间距作为主要优化对象。