流道截面形状对质子交换膜燃料电池性能的影响
颜敬昊,孙宾宾,高松
(山东理工大学 交通与车辆工程学院,山东 淄博255049)
燃料电池由于其高能量效率和环境友好性的优点而受到广泛关注[1-4]。在各种燃料电池中,质子交换膜燃料电池(PEMFC),因其高功率密度、高效率、快速启动、低工作温度(小于100 ℃)、无噪音等特点[5-9],被认为是电动汽车和便携式电源的下一代电源。双极板是PEMFC的重要结构之一,其主要作用是分隔反应气体,并通过流场将反应气体导入到燃料电池中,收集并传导电流,支撑膜电极以及承担整个燃料电池的散热和排水功能。双极板是燃料电池堆中体积最大、重量最大、成本最大的部件[10],而高成本正是影响燃料电池走向实用化的一大障碍。另外,双极板上的流道决定了其反应剂与生成物在流场内的流动方向、电池的散热能力及电池长期运行的稳定性[11]。目前,用于燃料电池双极板的流道结构生产成本高、效率低。因此降低双极板生产成本,将流道设计最佳化已成为亟待解决的问题。
质子交换膜燃料电池双极板不仅起到收集反应电流、支撑膜电极与联结单电池的作用,还对各电流密度、反应物与生成物的浓度分布产生重要影响;因此,合理的双极板结构设计对提高电池性能有重要意义,而在双极板结构研究中流道截面形状是关键因素之一。
本文采用流体力学计算方法,对矩形截面流道、三角形截面流道、梯形截面流道、燕尾型截面流道,圆形截面流道的质子交换膜燃料电池进行数值模拟。对比不同流道截面形状对电池性能的影响,为燃料电池流道截面形状的研究提供理论依据。
1 建模分析
燃料电池在工作时,反应气体进入流道后通过渗透的方式穿过具有孔隙率的气体扩散层(GDL),氢气到达阳极催化层,氧气到达阴极催化层完成电化学反应。在阳极,质子以水为载体穿过质子交换膜运输至阴极,反应生成的水存在于阴极催化层上,生成的水在阴极催化层通过向阴极GDL扩散到达阴极流道,经过气体吹扫的方式排出电池外。
电池正常工作需要水的存在,但水分含量须维持在适当范围内,水分含量不足将导致膜内质子传导困难,产生较大的欧姆损耗。气体在流道内如果分配不均匀或者流量不足,会导致部分区域燃料供应不足,反应无法持续进行,也会致使电池出现堵水。反应物的分布将决定电流密度分布,若电流密度分布均匀性差将产生局部热点,导致相邻区域质子交换膜含水量降低,影响膜内质子传递进而降低电池输出功率。
反应气体进入电池以及水排出电池都要经过双极板流场中的流道来实现,双极板的流场结构是影响燃料电池性能的重要因素之一,而流道截面的几何形状是双极板流场设计的重要部分。不同截面形状的流道对电池内气体浓度和水浓度的分布有重要影响。不同的流道截面形状会影响流道的高度、宽度、流道与GDL的接触面积等参数,这些参数的差异会影响气体和水在电池内的分布和传输。因此针对不同的流道截面形状需要搭建合理的仿真模型作为分析问题的基础。
1.1 几何模型
对不同截面形状的流道建立三维模型,模型的截面有5种,分别是矩形截面、三角形截面、梯形截面、燕尾形截面、圆形截面,几何模型如图1所示。

图1 几何模型
模型结构包括阳极流道、阳极GDL、阳极催化层、质子交换膜、阴极催化层、阴极GDL、阴极流道。由于不同的流道截面形状会影响流道的宽度和高度,导致不同截面的模型中流道截面面积、流道与GDL的接触面积产生差异,因此需要分别讨论模型截面具有相等的面积、流道与GDL有相等的接触面积时电池的性能。
将搭建的仿真模型分为两组进行讨论:
第一组中,每种流道模型的截面面积相等,流道长度相等;但是每种模型中流道的高度和宽度不相等,所以流道与GDL接触面积也不相等。模型几何参数见表1,几何图形如图2(a)所示。

表1 等截面面积流道模型结构参数

(a) 相等流道截面面积
第二组中,每种流道模型中,靠近GDL一侧流道宽度均相等,所以流道与GDL接触面积相等。每种流道模型的流道长度、流道高度均相等;但是每种流道模型的截面面积不相等。模型几何参数见表2,几何图形如图2(b)所示。

表2 等流道与GDL接触面积模型结构参数
第一组仿真模型保证了5种截面形状的流道都具有相同截面面积。第二组仿真模型保证了5种截面形状的流道都具有相同流道与GDL接触面积。
1.2 计算方法
采用三维计算流体力学 (CFD,computational fluid dynamics)数值模型,对模型内的有限网格单元进行求解。三维CFD数值模型能够准确反映电池中各物理量的空间分布,当选取单电池作为计算域时,CFD数值模型能够准确地反映出电池结构设计对电池内部传输过程及其性能的影响[12]。
1.3 数学模型
PEMFC运行时可看作是一个动态且多相的反应过程。PEMFC工作状态下伴随有气体在多孔介质中的扩散、流体的流动、水在电池内的传输、电子和离子的传递等,这些现象相互关联且相互影响,因此需要用详细的数学模型描述电池的工作过程。
PEMFC在工作过程中阳极的氧化反应与阴极的还原反应不间断的进行,因此反应过程中伴随着能量的释放与转换以及物质的消耗与生成,这些过程可用质量守恒方程、动量守恒方程、组分守恒方程、能量守恒方程、电流守恒方程、电化学方程等数学模型来描述。
流体力学中通用的微分方程表达式为[13]

(1)
式中:ρ为密度;ψ为求解变量;t为时间;u为速度;Γ为广义扩散系数;Sψ为ψ对应的源项。方程从左至右顺序出现的四项分别为瞬态项、对流项、扩散项和源项。
1.3.1 质量守恒方程
当ψ=1时,式(1)表示的电池内部质量守恒方程为

(2)
式中Sm表示质量源项。
1.3.2 动量守恒方程
当ψ=u时,式(1)表示的动量守恒方程为

∇·(Γ∇u)+Su,
(3)
式中源项Su为动量在多孔介质中的损失速率。在气体扩散层和催化层应用Darcy定律[14],源项Su可表示为
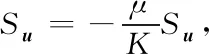
(4)
式中:μ为粘度系数;K为渗透系数。
1.3.3 组分守恒方程
当ψ=Yi(组分质量分数)时,式(1)表示的组分守恒方程为

(5)
式中:源项SYi为组分(氧气、氢气或水)在催化层内的消耗或产生速率;Di表示有效组分扩散系数。
1.3.4 能量守恒方程
当ψ=T(温度)时,式(1)表示的能量守恒方程为

(6)
式中:k为热传导系数;cp为比定压热容;ST表示温度源项。
1.3.5 电流守恒方程
当ψ=φH+或φe-(质子或电子电势),式(1)表示电流守恒方程。与流体动态过程相比,电化学反应时间很短,可以不考虑瞬态项,故电流守恒方程简化为:
∇·(σeff∇φH+)+SφH+=0,
(7)
∇·(keff∇φe-)+Sφe-=0,
(8)
式中:σeff和keff分别为质子传导率和电子传导率;SφH+、Sφe-分别为质子电势和电子电势的源项。
电化学反应即包括电荷转移也包括吉布斯能量的变化[15]。电化学反应的速率由电荷从电解质转移到固体电极所必须克服的活化能垒决定,反之亦然。电流是指电极表面上进行电化学反应的速率(释放或消耗电子的速率)。电流密度是指单位表面面积上的电流(电子或离子)。根据法拉第定律,电流密度与单位面积电荷的传递量和反应物的消耗速度成正比[16]:
i=nFj,
(9)
式中:n为转移的电子数;F为法拉第常数;j为单位面积的反应物的消耗速度。
1.3.6 电化学方程
电化学方程可用巴特勒-沃尔默(Butler-Volmer)方程[17]描述:

(10)
式中:i0是交换电流密度;αRd表示阴极还原反应电子转移系数;αOx表示阳极氧化反应电子转移系数;F为法拉第常数;E为电位;Er为可逆电位或平衡电位;R是气体常数;T是工作温度。
交换电流密度是对电极进行电化学反应准备程度的测度。如果交换电流密度较高,则电极表面较为活跃,交换电流密度越高,在任意电位下产生的电流也就越大,因此PEMFC的输出性能越好。
1.3.7 反应物与生成物流量计算
燃料电池入口处的反应物流量必须等于或高于电池内反应物的消耗速率。氢气和氧气的消耗速率与水的生成速率可由法拉第定律决定:
(11)
(12)
(13)

反应消耗的质量流量/(g·s-1)为:
(14)
(15)
水生成的质量流量/(g·s-1)为
(16)
1.4 仿真条件
所有的模型在相同的温度、进气压力条件下仿真,通入每个模型的气体加湿量、气体质量分数相同。
搭建的模型包括以下假设:(1)电化学反应在稳态下进行,流道中气体和液体以“层流”的方式流动;(2)通入模型中的氢气和氧气均为理想气体;(3)催化层、气体扩散层是各向同性且均匀的多孔介质,孔隙率恒定不变;(4)气体和液体之间没有相互作用;(5)忽略重力的影响。
2 模拟结果
根据仿真模型,观察三维模型中反应物和生成物的浓度变化来对模型的性能进行评估。对于反应物氢气和氧气,分别通过阴极和阳极的气体扩散层到达催化层参与反应,不同截面形状的流道会对反应气体的流速和压力产生影响,所以会影响气体向GDL扩散的速率以及分布情况,因此需要观察流道与GDL接触面上的气体浓度变化情况。生成物水在阴极催化层生成,通过气体吹扫以及扩散至气体扩散层,最后通过流道排出电池。不同截面形状的流道对水浓度的分布有不同的影响,因此需要观察阴极GDL与流道接触面的水浓度分布情况。
2.1 相等流道截面面积模型模拟结果
2.1.1 PEM中间截面电流密度分布
根据图3,三角形流道在PEM中间截面上产生的电流密度最大,圆形次之;但二者电流密度分布不均匀,差值较大,容易产生局部热点。燕尾形流道在PEM中间截面上的电流密度分布最均匀,电流密度的差值也最小。

图3 PEM中间截面电流密度分布
2.1.2 流道-GDL接触面氢气浓度分布
根据图4,圆形流道与GDL接触面上的氢气浓度分布最均匀,燕尾形流道与GDL接触面上的氢气浓度分布最不均匀;但差值小于0.1。

图4 流道-GDL接触面氢气浓度分布
2.1.3 流道-GDL接触面氧气浓度分布
根据图5,圆形流道与GDL接触面上的氧气浓度分布最均匀,燕尾形流道与GDL接触面上的氧气浓度分布最不均匀。

图5 流道-GDL接触面氧气浓度分布
2.1.4 流道-GDL接触面阳极水浓度分布
根据图6,圆形流道与GDL接触面上阳极水浓度分布最均匀,燕尾形流道与GDL接触面上水浓度分布最不均匀,且出口处水浓度较高。

图6 流道-GDL接触面阳极水浓度分布
2.1.5 流道-GDL接触面阴极水浓度分布
根据图7,圆形流道与GDL接触面上水浓度分布最均匀,燕尾形流道与GDL接触面上水浓度分布最不均匀,靠近出口处水浓度较高。

图7 流道-GDL接触面阴极水浓度分布
2.2 相等流道-GDL接触面积模型模拟结果
2.2.1 PEM中间截面电流密度分布
根据图8,圆形流道在PEM中间截面上产生的电流密度最大,三角形次之;但圆形流道电流密度分布最不均匀。燕尾形流道在PEM中间截面上的电流密度分布最均匀。

图8 PEM中间截面电流密度分布
2.2.2 流道-GDL接触面氢气浓度分布
根据图9,燕尾形流道与GDL接触面上氢气浓度分布最均匀,三角形流道与GDL接触面上氢气浓度分布最不均匀。

图9 流道-GDL接触面氢气浓度分布
2.2.3 流道-GDL接触面氧气浓度分布
根据图10,燕尾形流道与GDL接触面上氧气浓度分布最均匀,三角形流道与GDL接触面上氧气浓度分布最不均匀。

图10 流道-GDL接触面氧气浓度分布
2.2.4 流道-GDL接触面阳极水浓度分布
根据图11,在阳极燕尾形流道与GDL接触面上水浓度分布最均匀,三角形流道与GDL接触面上水浓度分布最不均匀,靠近出口出水浓度较高,不利于排水。
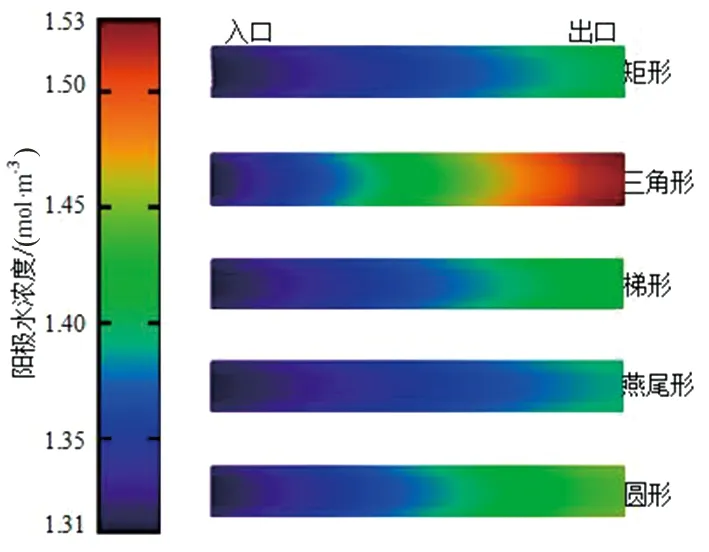
图11 流道-GDL接触面阳极水浓度分布
2.2.5 流道-GDL接触面阴极水浓度分布
根据图12,燕尾形流道与GDL接触面上水浓度分布最均匀,三角形流道和半圆形流道与GDL接触面上水浓度分布最不均匀。

图12 流道-GDL接触面阴极水浓度分布
2.3 结果分析
根据两大类型的仿真结果,圆形流道和三角形流道在PEM中间截面上产生的电流密度较大,但是分布均匀性最差;燕尾形流道电流密度分布均匀性最好。
在相等流道截面面积条件下,圆形流道水气分布均匀性最好,燕尾形最差;在相等流道与GDL接触面积条件下,燕尾形流道水气分布均匀性最好,三角形最差。
相等流道横截面积条件下,圆形流道与GDL接触面积最大,燕尾形流道与GDL接触面积最小;因为所有流道模型中流道的长度均相等,所以圆形流道体积最大,燕尾形流道体积最小。相等流道与GDL接触面积条件下,燕尾形流道截面面积最大,三角形流道截面面积最小;相同流道长度下,燕尾形流道体积最大,三角形流道体积最小。输入每个模型的气体流速、压力都是相同的,气体在体积小的空间内所受压力增大,加速了气体向GDL的扩散,气体也将更快的到达催化层,加快化学反应速率;因此,反应物的消耗速率以及生成物的生成速率都会加快,使反应物和生成物在PEMFC内传输速率加快,造成气体和水分布不均匀的情况。
3 结论
1) PEMFC气体和水分布的均匀性与流道体积有关,体积越大分布越均匀,体积越小分布越不均匀;但并不是流道体积越大越好,当流道体积超过一定范围后,一方面不利于生成物水的及时排除,另一方面对双极板的生产加工、装配也是极大的考验。
2)影响PEM中间截面的电流密度分布的是流道截面形状,而不是流道尺寸参数。圆形和三角形流道产生的电流密度最大,分布的均匀性最差;燕尾形流道电流密度分布的均匀性最好。

