风电工程中负切变现象的分析研究

吴 莎，余官培，卢 胜，朱一凡，汪 健，万鹏飞

(湖北省电力勘测设计院有限公司，武汉 430040)

0 引言

准确分析风电机组轮毂高度处的风资源是估算风电场发电量的先决条件。在实际的风电场工程中，往往测风塔的测风高度与风电机组的轮毂高度不一致，因此，通过合理的风廓线推算出目标高度的风速情况显得尤为重要。通常，风廓线由幂指数模型来表示，以风切变指数来表征风速随高度变化而变化的情况。在实际风电工程中，会出现某层高度间的风切变指数为负值的情况，即负切变现象，这会造成风速外推计算的不准确性，从而影响风电机组的点位布置及其轮毂高度的选择。

HELLMAN[1]提出的幂指数风切变模型是目前最常用的、简单可行的计算风切变指数的公式，但幂指数形式的风切变模型忽略了粗糙度与大气热稳定性等因素对风廓线的影响。PANOFSKY等[2]提出了利用大气热稳定性函数和粗糙度来评估风切变指数的经验公式。PASQUILL[3]把大气热稳定性分为了5个等级，即：极不稳定、不稳定、中性、弱稳定、稳定。刘玮等[4]分析了不同大气热稳定性的判定参数，并结合大气热稳定性提出了新的风廓线外推模型。贺德馨[5]分析了不同地形对风特性的影响情况。但目前的研究中对实际风电工程中的负切变现象普遍缺乏分析研究。

基于此，本文对风电工程中负切变现象的主要影响因素进行了分析研究。针对粗糙度、复杂地形及大气热稳定性这3种条件分别对风切变特性的影响进行了分析，归纳了实际工程中常见的典型场景下的负切变现象，提出了合理的风切变特性分析方法，并给出了不同影响条件下风电机组的点位排布与风电机组轮毂高度选取的建议。

1 风切变模型及判定参数

1.1 风切变模型

风切变是指水平风速随高度变化而产生的变化，风切变的轮廓称为风廓线。本文所研究的风速均为水平风速。

风切变指数计算公式为：

式中，z1、z2为不同高度层的离地高度，m；u1、u2为z1、z2高度层的风速，m/s；α为风切变指数，其值与下垫面粗糙度、大气热稳定性、复杂地形有关。α值的大小决定了水平风速在垂直方向上的变化程度，表征风速随高度增加的快慢，α值大，表示风速梯度大；α值小，表示风速梯度小。

1.2 负切变现象

一般情况下，大气边界层中，水平风速随着高度的增加而增加，通常会呈现出幂指数模型形式的风廓线分布，如图1a所示。风切变指数越大，风速的大小随高度变化产生的变化越剧烈。在某些特殊情况下，尤其在复杂地形条件下，容易出现负切变现象，如图1b所示。负切变往往会造成风速外推计算的不准确性，从而影响风电机组轮毂高度的选择，并影响对风电机组轮毂高度处风资源的分析结果。

图1 幂指数模型形式的风廓线分布Fig. 1 Wind profile distribution in form of power exponential model

1.3 粗糙度的概念

粗糙度是与粗糙程度相关的一个常数，表示下垫面风速为零的离地高度。下垫面是指与大气下层直接接触的地球表面，包括海洋、陆地及陆地上的高原、山地、平原、森林、草原、城市等。不同的下垫面粗糙度条件下，风廓线的差异很大。常见的下垫面的粗糙度经验取值如表1所示。

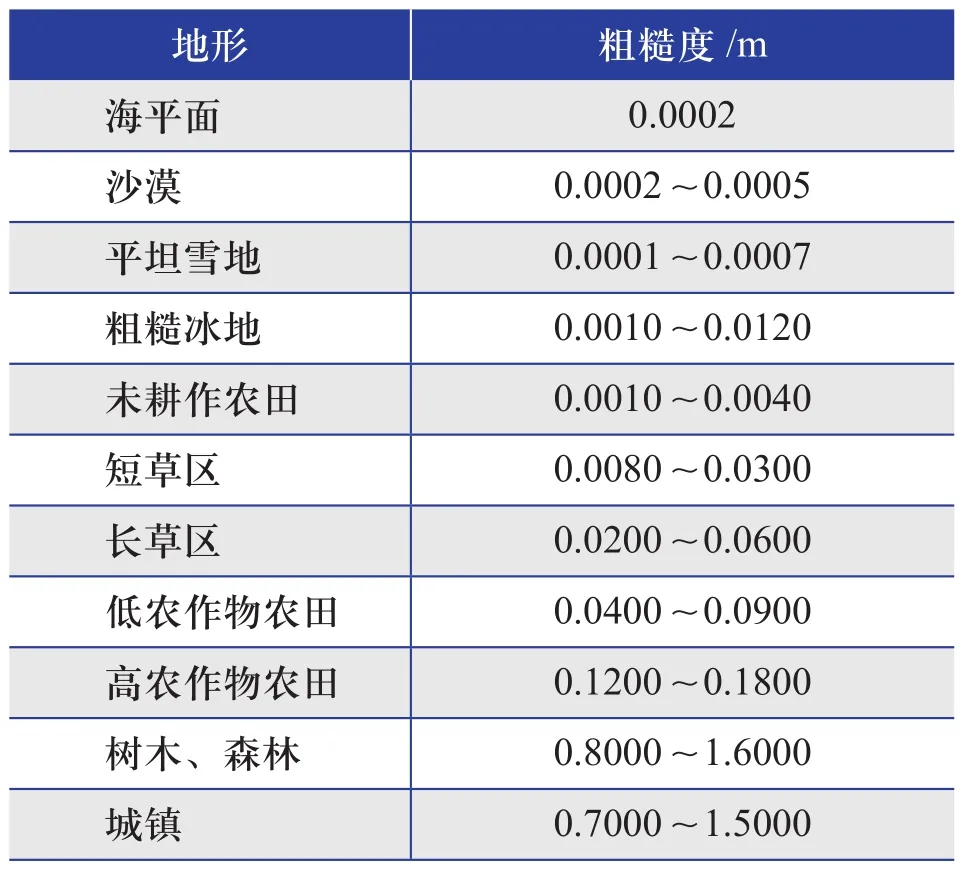
表1 常见的下垫面的粗糙度经验取值Table 1 Empirical values of roughness of common underlying surfaces

1.4 大气热稳定性及其判定方法

大气热稳定性是指大气受到了垂直方向上的扰动后，能否回到原来的平衡位置的一种特性。大气热稳定性主要受太阳辐射与风速的影响。根据当前的理论，大气热稳定性可分为6个等级，即：极不稳定(A)、不稳定(B)、较不稳定(C)、中性(D)、较稳定(E)、稳定(F)。

常用的大气热稳定性的判定方法主要包括：

1)梯度理查森数判定方法。梯度理查森数Ri

[6]是通过风速、温度梯度来判断大气的热稳定性，对风速、温度参数的精度要求较高。

2)总体理查森数判定方法。当风电场场区的跨度较大、测风数据的时间尺度较长时，可用总体理查森数RiB[7]代替Ri。

3)水平风向标准差判定方法。当测风塔无温度梯度数据时，可采用水平风向标准差σθ[8]来计算大气热稳定性。该方法适用于平坦开阔地形。

4)垂直温度梯度判定方法。垂直温度梯度ΔT/Δz(其中，ΔT为不同高度层的温差；Δz为高度差)[8]可反映热力湍流的影响，以此来判定大气热稳定性。

5)风速比判定方法。风速比UR反映了大气湍流扩散能力，适用于风速大、稳定性级别高的大气热稳定性判定。

6) Monin-Obukhov判定方法。Monin-Obukhov的长度L[6]表征了湍流切应力和浮力对湍动能贡献的相对大小，可以此来判定大气热稳定性。

在上述常用的大气热稳定性的判定方法中，由于RiB对风速、温度梯度的精度要求较低且适用范围广，因此，本文选择总体理查森数判定方法进行分析。

RiB的计算公式为：

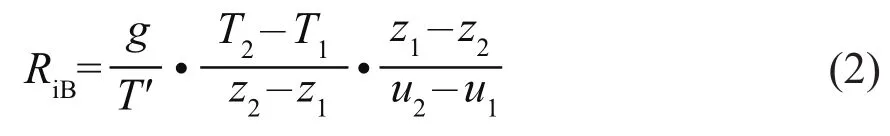
式中，g为当地的重力加速度；T2、T1分别为上、下高度层的温度；T′为上、下高度层的平均温度。

不同学者基于RiB提出了各自不同的判定大气热稳定性的等级划分标准，具体如表2所示。

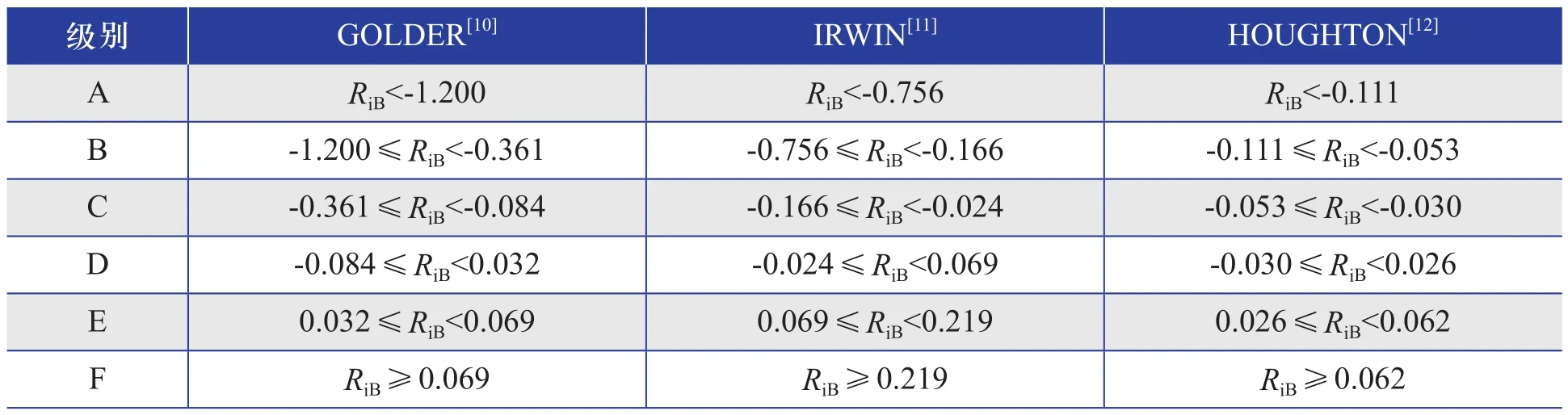
表2 不同的基于RiB的大气热稳定性的等级划分标准Table 2 Different classification criteria of atmospheric thermal stability based on RiB

2 负切变现象的成因分析

2.1 下垫面粗糙度造成的影响

粗糙的表面比光滑的表面更容易在近地层中形成湍流，使风速充分垂直混合。混合作用加强会使近地层的风速梯度减小，而梯度风的高度增高，即粗糙度高的下垫面比粗糙度低的下垫面到达梯度的高度更高，所以粗糙的下垫面层中的风速比光滑的下垫面层中的风速小。

而在2种粗糙度类型的下垫面相接的过渡段，下风向的风要经过一段距离才能使其状态重新适应新的粗糙度情况，此时风廓线就会变得十分复杂。当风由光滑的下垫面吹向粗糙的下垫面时，风廓线形状会在近地层部分变窄，使上高度层的风切变指数比下高度层的大，就会在风廓线中部形成1个拐点；当风从粗糙的下垫面吹向光滑的下垫面时，风廓线形状会在近地层部分变大，使上高度层的风切变指数比下高度层的小，从而导致风廓线中部出现负切变现象。其中最典型的案例就是潮间带海上风电场，当风从陆地吹向海洋时，就容易出现负切变现象；而当风从海洋吹向陆地时，风廓线就容易出现拐点。不均匀粗糙度对风廓线的影响如图2所示。

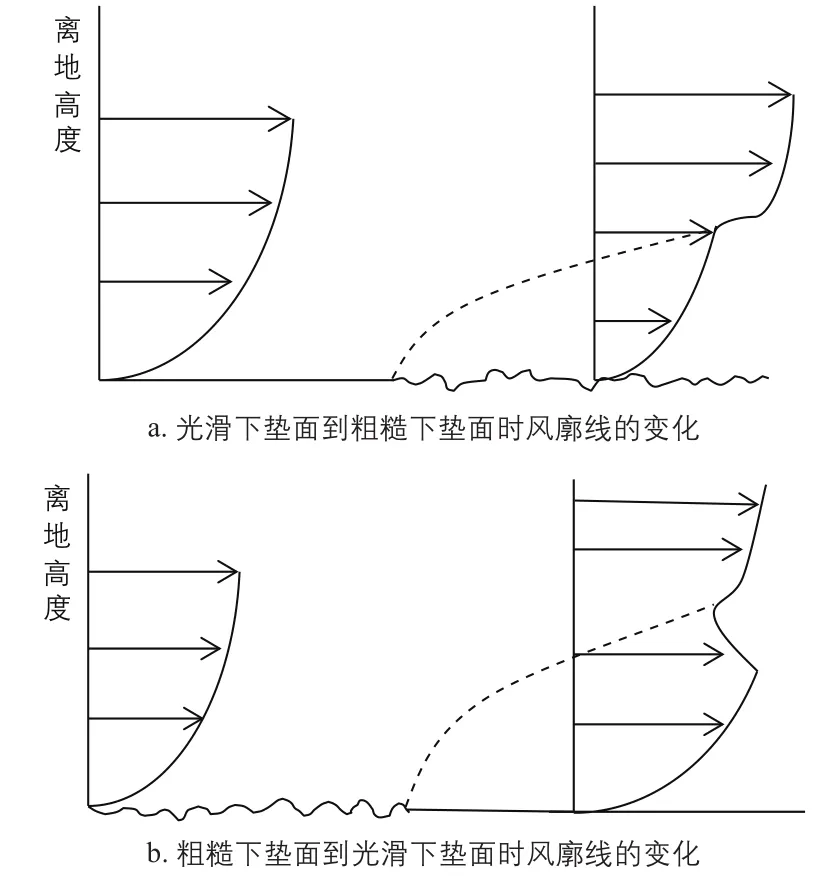
图2 不均匀粗糙度对风廓线的影响Fig. 2 Effect of uneven roughness on wind profile

2.2 复杂地形造成的影响

地形对大气边界层中的风特性影响十分显著。一般来说，山地地形可分为2类：隆升地形和低凹地形。局部地形的上升或下降都会使气流改变方向，而且相邻地方的风速方向可能差异很大。隆升地形可对风产生加速效应，当山脊与风向正交时，气流沿着上升地形不断汇集，在山脊顶部区域加速最大；然后气流在越过山脊后，压力减小，风向发生变化，形成负压区；最后在山区的背风侧形成低速的回流。风与不同形状的山脊相交产生的风廓线均不相同。抬升坡度使靠近地面部分的风加速变快，而地面上方高处的风速受到的影响较小，最终使底层的风速大于高层的风速，产生负切变现象。当隆升地形的坡度过于陡峭时，就形成了山崖，风的整个流场在山崖正面部分会开始产生分离，气流减速；然后跨过山崖顶点时气流加速；最终会形成复杂的流动性风廓线和产生旋涡区[9]。

2.3 大气热稳定性造成的影响

一般是在低风速情况下需要考虑大气热稳定性对风廓线的影响，当风速小、云量少时，白天的大气热稳定性呈不稳定，但晚上的大气热稳定性呈稳定；而当风速大、云量多时，白天和晚上的大气热稳定性通常呈中性稳定。大气热稳定性与热浮力相关，而低风速时由热浮力引起的气流上升速度相对较大。

一天之中，大气边界层的热稳定性会出现从稳定到不稳定的状态变化，风廓线形状和大气边界层厚度均会产生明显的变化。在晚上，地表气温降低，大气热稳定性呈稳定状态，大气边界层厚度减小，风速变大，对应的风切变指数较大；而在白天，尤其是中午，在太阳辐射下，地表气温上升，产生上升气流，大气热稳定性呈不稳定状态，大气边界层厚度变大，风速减小，对应的风切变指数较小。当大气边界层中出现逆温层时，温度切变呈现负值；此时上高度层对应的风切变指数小，而下高度层对应的风切变指数大，中间层就会出现负切变的现象。

3 实际风电场中的典型负切变现象的分析

本文分别以福建省某近海潮间带海上风电场、属于复杂地形的湖北省某山地风电场、属于温度变化剧烈区域的东南亚某平原风电场作为算例，分析了粗糙度、复杂地形、大气热稳定性对风切变的影响，并对实际风电场工程中的典型负切变现象进行了分析。

3.1 算例1——粗糙度对风切变的影响

本段分析以福建省某海上风电场为例。由于该项目属于近海潮间带风电场，大气热稳定性呈中性稳定，因此本算例主要分析陆地与海平面的粗糙度变化对风切变的影响。

3.1.1 风电场测风塔的数据分析

该海上风电场的测风塔的离岸距离为3.5 km，距离陆地较近。该海上风电场区域的测风塔位置示意图如图3所示，图中，FJ1#测风塔测得的整体α平均值为正值，约为0.0387。

图3 本算例海上风电场的测风塔分布情况示意图Fig. 3 Distribution diagram of anemometer tower in this example of offshore wind farm

对FJ1#测风塔测得的不同高度处的风速数据以不同扇区进行统计，平均风速分布结果如图4所示。

由图 4 可知，从 0°～180°扇区及 315°～360°扇区方向来风时，FJ1#测风塔测得的风速在不同程度上出现了负切变现象。其中，在90.0°～157.5°扇区之间，在70～85 m高度层出现了明显的负切变现象；在0°～67.5°扇区之间，在50～70 m高度层出现了轻微的负切变现象，50 m高度处的平均风速与70 m高度处的平均风速几乎相同。

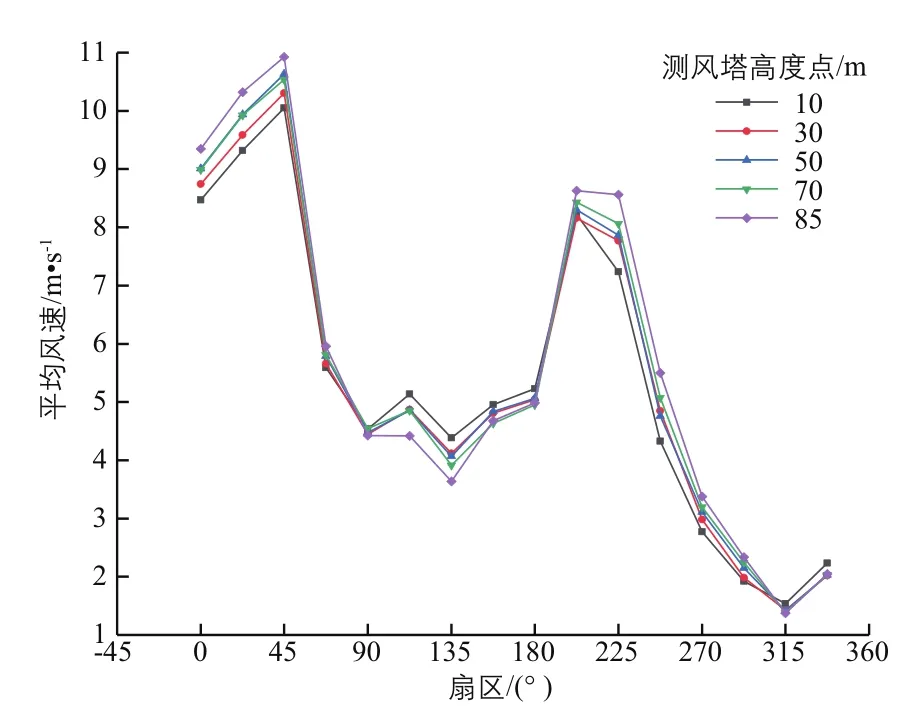
图4 FJ1#测风塔测得的不同高度处不同扇区的平均风速分布情况Fig. 4 Distribution of average wind speed in different sectors at different heights measured by FJ1# anemometer tower

FJ1#测风塔测得的风速具有代表性的出现负切变现象的扇区的风廓线图如图5所示。

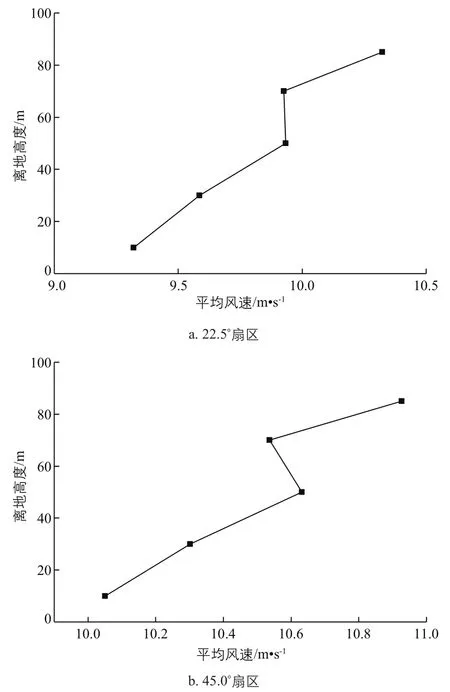
图5 FJ1#测风塔测得的风速出现负切变现象的扇区的风廓线图Fig. 5 Wind profile of sector with negative shear phenomenon in wind speed measured by FJ1# anemometer tower

从图5可以看出，该近海潮间带海上风电场场区内风廓线明显受到了陆地粗糙度的影响。陆地部分(树木、森林)的粗糙度为0.8～1.6，海面的粗糙度为0.0002，来流风先经过陆地再经过海面，存在明显的粗糙度过渡情况。来流风从陆地的粗糙地面吹向海面的光滑面时，风廓线形状在近地层部分变大，上高度层风速还没有适应新的粗糙度情况，则上高度层的风切变指数比下高度层的小，导致了70～85 m与50～70 m高度层间出现了负切变现象。风速越大，其受下垫面粗糙度的影响也就越大，风廓线产生变化的区域越靠近地面，所以在0°～67.5°扇区中出现的负切变现象的中间层高度比在90°～135°扇区中的低。

3.1.2 粗糙度对风电机组的点位布置及其轮毂高度选取的影响

针对粗糙度对风电机组的点位布置及其轮毂高度选取的影响进行分析，得出以下结论：

1)在粗糙度存在明显过渡的情况下，建议分扇区对风速进行分析，结合主风向及主风频方向与粗糙度过渡方向的对应关系，考虑是否会出现风从粗糙下垫面吹向光滑下垫面而产生负切变现象，从而进行分扇区风切变条件下的风电机组轮毂高度的论证分析。

2)选取风电机组轮毂高度时，若出现了负切变现象，则选取的风电机组轮毂高度需避开产生负切变现象的中间层。建议在粗糙度存在明显变化的区域建立测风塔时，适当增加测风高度，以探明产生负切变现象的中间层位置及风切变的变化趋势。

3.2 算例2——复杂地形对风切变的影响

以湖北省某山地风电场为例，该项目所在地的海拔高度不高，温度切变属于正常变化；风电场下垫面以杂草为主，不存在粗糙度突变的情况。但由于该项目地形复杂，测风塔北侧和东北侧、东南侧及西侧均有比该项目所在地海拔更高的山脊，项目所在区域分布有山脊、沟谷，导致地形对气流运动的影响较大，因此，本算例主要是基于复杂地形条件下的测风数据分析复杂地形对风切变的影响。

3.2.1 风电场测风塔测得的风速数据分析

该山地风电场位于山地区域，海拔为200～300 m，区域地表植被主要为杂草，有少量树木。该山地风电场的测风塔位置示意图如图6所示，图中，HB1#、HB2#为测风塔编号。

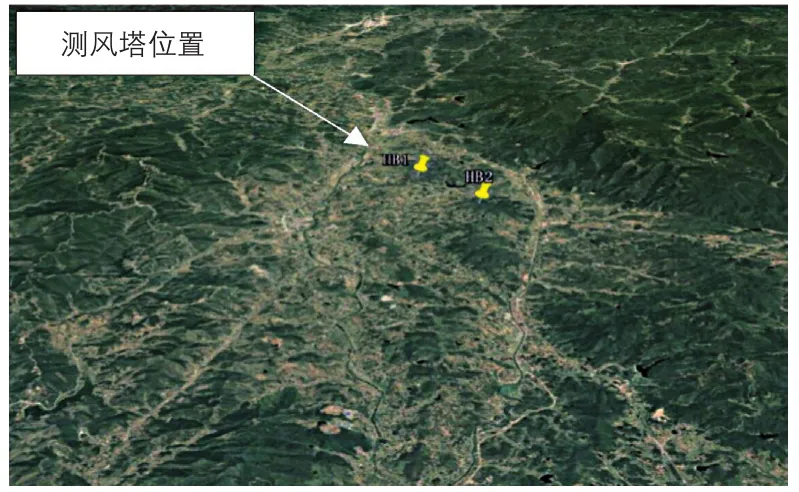
图6 本算例山地风电场的测风塔位置示意图Fig. 6 Location diagram of anemometer towers in this example of mountain wind farm

分析HB1#测风塔与HB2#测风塔的同期数据，对测风塔测得的不同高度处的风速数据分扇区进行统计，结果如图7所示。

图7 HB1#和HB2#测风塔测得的各高度处的分扇区平均风速分布图Fig. 7 Distribution of average wind speed by sector at each height measured by HB1# and HB2# anemometer towers

从图7中可以看出，HB1#测风塔及HB2#测风塔所在区域在70 m及以上高度多层临近高度之间出现了负切变现象；尤其从HB2#测风塔测得的风速曲线来看，在90～100 m高度层近似为等风层，然后在100～120 m高度层再次出现比较明显的负切变现象。

从图7还可以看出，HB1#测风塔与HB2#测风塔测得的风速均出现了负切变现象，出现负切变现象的扇区主要集中在0°～135°扇区及225.0°～337.5°扇区，这与周边山脊区域的分布方向和高度一致。

HB1#测风塔与HB2#测风塔测得的风速出现负切变现象的具有代表性的扇区的风廓线图如图8所示。

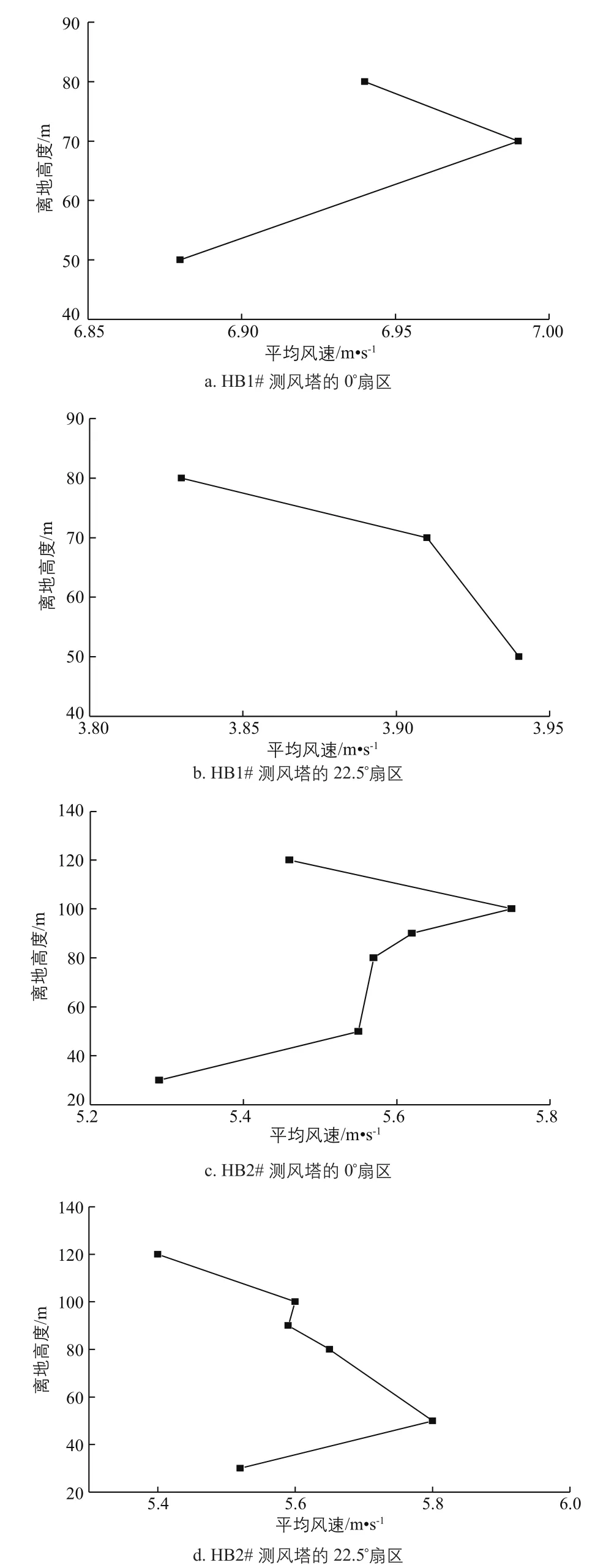
图8 HB1#测风塔与HB2#测风塔测得的风速出现负切变现象的扇区的风廓线图Fig. 8 Wind profile of sector with negative shear phenomenon in wind speed measured by HB1# and HB2# anemometer towers

从图8可以看出，复杂地形造成的加速效应产生了负切变现象。HB1#测风塔与HB2#测风塔距离周边高大的山脊较近，产生负切变现象的风速方向主要在0～135°扇区，与山脊正交。气流沿着山脊不断上升汇集，在山脊顶部区域加速最大，使贴近山脊的底层的风速比其上方高处的风速大，从而产生了明显的负切变现象。

3.2.2 隆升地形产生的加速效应仿真

隆升地形条件下风流场的流场特性图如图9所示。图中，X代表水平距离，Z代表离地高度。

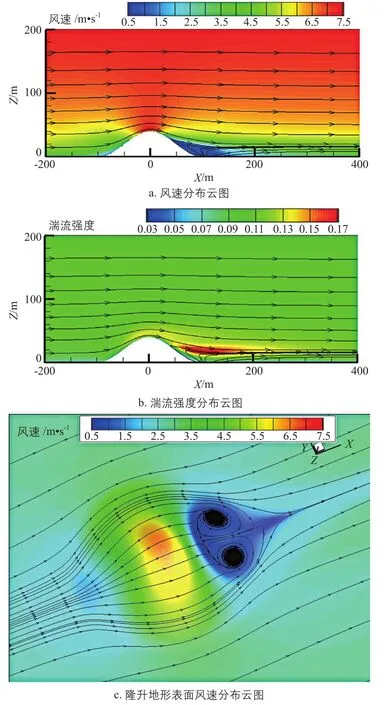
图9 隆升地形条件下风流场的流场特性计算结果Fig. 9 Calculation results of flow field characteristics of wind flow field under hilly terrain

根据图9可知，当气流经过隆升地形时，在迎风面的山脚处由于逆压梯度，流场边界层厚度迅速增大，气流出现较小的减速区。在迎风面，在气流沿地形上升过程中，气流受到地形的挤压而产生加速效应，且风速随山坡高度的升高而增大，在山顶处风速大、湍流强度小，山顶的流场边界层厚度因风加速作用变小。随后在背风面处，风速随着山坡高度的降低而不断减小，在背风面表面上形成旋涡，并在背风面下游处形成一个低速的回流区，该低速回流区内风速小、湍流强度大。

当气流通过山地、丘陵或山脊时，由于受到了地形阻碍的影响，在山的迎风面下部，风速减弱、气流上升；在山的顶部和两侧，气流线变密，风速增大；在山的背风面，气流线呈辐散状，风速减弱，且有下沉气流，在重力和惯性力的作用下使山脊背风面气流呈现波状流动。山地地形对风速的影响水平距离一般是迎风面山高的5～10倍距离，是背风面山高的15倍距离。山脊越高，坡度越缓，背风面受影响的水平距离越远。

背风面水平距离X与山高h与山的平均坡度β之间存在关系，即：

式中，k为比例常数。

3.2.3 复杂地形对风电机组的点位布置及其轮毂高度选取的影响

针对复杂地形对风电机组的点位布置及其轮毂高度选取的影响进行分析，得出以下结论：

1)周边山脊对风流场的影响比较显著，由于遮挡，回流区现象比较明显，因此在进行风电机组点位布置时应尽量考虑远离山脊背风侧。该山地风电场场区的来风方向主要集中在正北、正南及周边方向，南向来风未出现负切变现象，北向来风出现的负切变现象明显，所以在对风电机组进行点位布置时要特别考虑北部山脊对该山地风电场场区的影响。

2)复杂地形条件下，负切变现象的出现与地形分布相关，存在整体呈现为正常切变但局部扇区呈现负切变的情形。在复杂地形条件下，进行精细化风资源论证分析时，建议将风速分扇区进行分析，从而可以全面了解各扇区的风资源情况特征。

3)鉴于该山地风电场区域内的风切变分布规律，场区中风电机组的轮毂高度的选择可以根据不同区域分别考虑。

4)对于由复杂地形导致的负切变现象严重的区域，可在负切变出现的扇区进行加密测风，以探明负切变现象的影响范围，从而指导并确定风电机组轮毂高度的选取方案。

3.3 算例3——大气热稳定性对风切变的影响

以东南亚某平原风电场为例。该地区的光照强烈，太阳辐射强；昼夜温差大且不同季节温差大；大气热稳定性变化大；海拔高度低，属于海拔37 m以下的滨海平原。风电场的下垫面地势平坦，为沙质土壤，种植有松树，测风塔位于海滨陆上区域的简单地形区域，不存在从粗糙下垫面向光滑下垫面过渡的情况，以及因复杂地形而产生的负切变现象，此时负切变现象主要是因大气热稳定性的影响而产生的。因此，本算例主要分析大气热稳定性对风切变的影响。

3.3.1 风电场测风塔数据分析

东南亚某平原风电场处于约13°N的位置，风电场东侧距离海边约6 km。该平原风电场的测风塔位置示意图如图10所示，图中，YN1#为测风塔编号。

YN1#测风塔的测风数据显示，其α约为0.311，在78 m高度处的风速略低于70 m高度处的风速，出现了负切变的现象。由于该区域温差变化随昼夜、季节的变化巨大，因此YN1#测风塔设有4 m与76 m双层高度温度测量仪，2个高度处的温差在0～2.6 ℃之间。YN1#测风塔在4 m与76 m高度处的温度均呈现以下2个特征；一个是夏季高、冬季低，季节温差约为6～9 ℃；另一个是午间高、夜间低，早晚温差约为6～8 ℃。

对YN1#测风塔测得的不同高度处的风速数据按照逐月、逐小时分别进行统计，具体如图11所示。

图11 YN1#测风塔测得的各高度处的逐月、逐小时平均风速分布图Fig. 11 Distribution of monthly and hourly average wind speed at each height measured by YN1# anemometer tower

从图11可以看出，YN1#测风塔测得的风速出现了负切变现象。其中，一年之中的负切变现象主要出现在冬季，一天之中的负切变现象主要出现在晚上。

大气的热稳定性变化导致了负切变现象的产生：白天太阳辐射强，地表温度高，大气热稳定性为不稳定状态，当进入夜晚时，地面温度骤降，该风电场场区临近海洋，上高度层的温度变化慢，最终导致靠近地面部分的温度比其上高度层的温度低，产生了逆温层。下高度层温度低，风切变指数大；上高度层温度低，风切变指数小，因此，中间层部分产生了负切变现象。

3.3.2 平原风电场区域的大气热稳定性分析

依据表2中HOUGHTON[12]提出的大气热稳定性等级划分标准，计算该平原风电场区域的逐月、逐小时RiB值，并根据该值对大气热稳定性进行分类，绘制大气热稳定性状态分布图，如图12所示。

图12 平原风电场区域的逐月、逐小时大气热稳定性分布图Fig. 12 Distribution of monthly and hourly atmospheric thermal stability state in plain wind farm

针对该平原风电场区域的大气热稳定性等级的占比情况，以及不同大气热稳定性等级下α的平均值进行统计，如图13所示。

从图13a可知，该平原风电场区域受大气热稳定性的影响很大，大气热稳定性为不稳定状态(包括极不稳定A与不稳定B)约占40%；大气热稳定性为中性状态（包括较不稳定C与中性D)约占19%；大气热稳定性为稳定状态(包括较稳定E与稳定F)约占41%。该平原风电场区域的整体大气热稳定性状态表现为：午间不稳定，晚间较稳定；夏季不稳定，冬季较稳定。

图13 平原风电场区域的大气热稳定性等级占比及不同大气热稳定性等级下α的平均值Fig. 13 Proportion of atmospheric thermal stability grades and α mean under different atmospheric thermal stability grades in plain wind farm

从图13b可知，该平原风电场区域基本呈现大气热稳定性越稳定，α平均值越高的趋势。当大气热稳定性处于不稳定状态时，受到热浮力的影响，垂直方向风速流动加大，水平方向风速小，大气边界层厚度变大，α平均值减小；当大气热稳定性处于稳定状态时，垂直方向风速流动减小，水平方向风速大，大气边界层厚度减小，α平均值增大。

3.3.3 大气热稳定性对风电机组的点位布置及其轮毂高度选取的影响

针对大气热稳定性对风电机组的点位布置及其轮毂高度选取的影响进行分析，得出以下结论：

1)对于温差变化明显或大气热稳定性变化明显的区域，在对其进行风资源分析时，需要分时段、分季节来评估α值的大小，以此来分段进行合理地风速外推。

2)从测风塔的数据来看，YN1#测风塔在70～78 m高度区域出现了负切变的现象，70 m与78 m高度层之间的平均风速相当。综合考虑后，当选取低轮毂高度时，选取高70 m左右的轮毂高度即可；当选取高轮毂高度时，需要通过分时段、分季节的α值进行合理的高度风速外推后，再考虑高轮毂高度的选取值。另外，建议在大气热稳定性变化明显的区域建立测风塔时应适当增加测风高度，以探明负切变的中间层位置及风切变的变化趋势，以便确定技术经济性最为合理的风电机组轮毂高度。

4 结论

本文分析了风电工程中负切变现象的成因，并分析了粗糙度、复杂地形和大气热稳定性对风切变产生的影响。在分析负切变现象时，在粗糙度为影响因素的情况下，需要分扇区同时结合主风向对测风塔数据进行综合分析，并且分析了粗糙度过渡段的风廓线的变化情况；在复杂地形为影响因素的情况下，需要分扇区分析测风塔测得的风速数据，并提出了地形对风速的加速效应，以及隆升地形会在背风侧产生回流区，造成风速减小、湍流增大的情况；在大气热稳定性为影响因素的情况下，需要分时间、分季节对测风塔测得的风速数据进行分析，并采用总体理查森数判定方法对该区域的大气热稳定性进行了分类，然后分析了该区域风切变指数的变化情况。在得出以上结论的基础上，提出了在粗糙度、复杂地形、大气热稳定性这3种影响因素下产生负切变现象时，应如何进行合理的风电机组点位布置及其轮毂高度的选取，实现了更加精细的风资源评估。最后归纳了实际风电工程中常见典型负切变现象，提出了合理的风切变特性分析方法，为今后的风电工程应用提供了典型范例。