信息筛选多任务优化自组织迁移算法

程美英，钱 乾，倪志伟，朱旭辉

（1.湖州师范学院经济管理学院，浙江湖州 313000；2.浙江省教育信息化评价与应用研究中心，浙江湖州 313000；3.湖州师范学院教师教育学院，浙江湖州 313000；4.合肥工业大学管理学院，合肥 230009）

（∗通信作者电子邮箱02550@zjhu.edu.cn）

0 引言

自组织迁移算法（Self-Organized Migrating Algorithm，SOMA）［1］是一种新型基于群体的智能优化算法，自2004 年提出至今已得到广泛研究，现有成果主要集中于两方面:1）改进SOMA，弥补易陷入局部最优、收敛速度慢、求解精度低等缺陷。文献［2］引入机会策略产生扰动向量，提供比基本SOMA更多的位置选择来增强个体寻优能力；文献［3］在SOMA 中引入自适应参数控制、领导个体选择及给最优个体建立外部档案等策略提高种群多样性；文献［4］在每次迭代过程中按照与领导者的欧氏距离均匀选择粒子进行移动，提高SOMA 收敛速度和精度等。2）将SOMA 应用于解决实际优化问题。文献［5］在可重构制造业中引入SOMA 最小化机器模块变化；文献［6］将SOMA 用于机器人躲避动态障碍物并抓取移动目标；文献［7］引入SOMA解决多层次图像阈值分割问题等。

基于群体的智能优化算法通过个体之间的协作能“涌现”出智能行为，实则具有隐含并行性，而这种并行性表现在两方面:一是算法的内在并行，即本身适合大规模并行；二是算法的内涵并行性，群体智能算法采用种群的方式组织搜索，因而可以搜索解空间内的多个区域，并相互交流信息，具备很强的多任务优化能力（多任务优化指在某一时刻同时处理多个不同的优化问题［8］）。基于群体智能算法的多任务优化［9］概念开创了将具有“隐”并行性的进化算法应用于多任务处理的新局面。文献［9］首次探索多因子遗传机制，提出多任务处理多因子进化算法（MultiFactorial Evolution Algorithm，MFEA），在多层次多任务优化［10］、多目标多任务优化［11］等领域中均得到较好应用；文献［12］在MFEA 基础上，引入拟牛顿迭代、重新初始化部分适应值较差解、自适应选择策略，提高MFEA 求解多任务性能；文献［13］通过实验证明MFEA 可保持种群的动态多样性，但MFEA 的本质在于有效信息传递；文献［14］以数据驱动获取任务之间的相关信息，自适应实现任务之间的信息传递；文献［15］基于闭式解自动降噪编码器显示实现多任务之间映射；文献［16-17］首次将自然界生物种群中的协同进化机制与粒子群算法相结合，子种群间按一定概率或连续停滞若干代后交互信息，实现多任务优化；文献［18］引入等级因子、标量因子和技能因子构造多任务环境，每次让最合适的粒子求解最合适的任务。

现有SOMA 关注点主要集中在单个任务优化上，在多任务优化领域研究甚少，且现有关于在多任务优化领域如何避免无关信息共享造成“负迁移”现象的研究成果并不多。基于上述问题，本文的主要工作为:通过有效探索SOMA 的“隐并行性”，共享和协调种群中有效信息，实现多任务优化，然后引入信息筛选机制有效遏制多任务负迁移消极影响，提出信息筛选多任务优化自组织迁移算法（SOMA for Multi-task optimization with Information Filtering，SOMAMIF）。仿真实验以一组函数优化问题和一组离散优化问题为例验证了SOMAMIF的有效性。

1 基本SOMA描述

SOMA 的社会生物学基础是社会环境下群体的自组织行为，如一群动物在寻找食物时，若某一个体率先发现食物，则成为群体领先者，其他个体通过改变自身运动方向迁移至领先者附近，在搜索过程中某个体若比先前领先者更为成功，则它成为群体中新的领先者，其他个体再次改变运动方向迁移至该新领先者所在位置，直至达到或接近全部最优解。SOMA基本步骤如下:

步骤1 初始化种群中个体位置和所有参数。

步骤2 计算所有个体适应值。

步骤3 比较得出当前领先者位置。

步骤4 按式（1）得出参数PRTVector。

步骤5 按式（2）更新个体位置。

步骤6 判断是否满足循环结束条件，若不满足，转步骤2。

步骤7 输出全局最优解。

PRTVector依赖于PRT:若随机 数rand小 于PRT，则PRTVector取值1，否则为0，如式（1）所示。

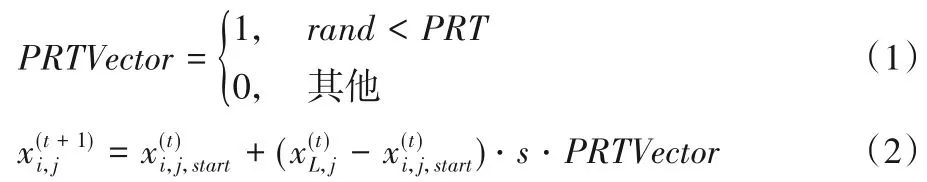
2 多任务SOMAMIF

为形象描述多任务环境中的信息迁移模式，这里仅以同时求解极小函数优化问题f1和f2为例，如图1 所示。假设f2全局极值点位于B点，在AB区域，函数f1和f2的单调趋势相反，当f1传递信息给f2，必会使得f2偏离极值点（信息负迁移）；而在BC区域，当f1传递信息给f2，必会加速f2收敛至极值解（信息正迁移）。若能利用BC区域的有效信息，将任务f1和f2绑定同时求解，必能同时加速f1和f2的收敛速度并提高二者的求解质量。

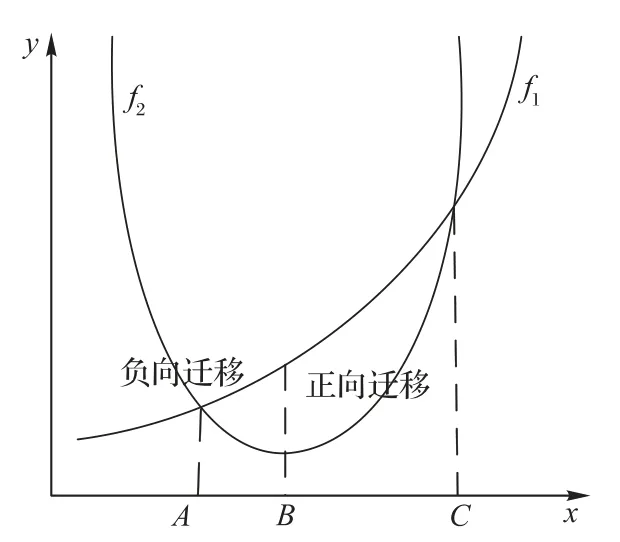
图1 多任务信息迁移Fig.1 Multi-task information transfer

2.1 多任务SOMAMIF搜索空间设置

多任务环境中不同任务一般处于不同的维度，构建统一多任务搜索空间，使得不同维度的任务仍然可以传递有效信息。假设需要同时处理K个任务T1，T2，…，TK，任务Ta（a=1，2，…，K）的搜索空间和维数分别设为ψa和da，令多任务统一搜索空间Ψ=ψ1∪ψ2，…，∪ψK，维 数D=max｛d1，d2，…，dK｝，对Ta解码时，只需取D的前da维。

2.2 多任务SOMAMIF信息筛选和迁移模式

在多任务环境中，无关的信息共享可能伤害多任务处理性能，即出现信息“负迁移”［8］，进而抑制干扰多任务优化性能，这是目前尚未完全解决的难题之一，本文引入信息筛选机制有效遏制“负迁移”消极影响。

假设需要同时处理K个任务，则随机产生K个SOMA 子种群，子种群Pa（a∈{1，2，…，K}）用于处理任务Ta。各子种群在执行基本SOMA 的同时，实施如下的信息筛选和迁移过程，具体步骤如下:

步骤1 信息交互愿望（需求）。当任务Ta连续若干代停滞进化时，子种群Pa产生信息交互需求，即达到信息交互节点γ。

步骤2 信息获取来源。自然界中的物种并非彼此孤立，生活在同一环境中的物种/种群通过交互信息达到共同进化。当任务Ta产生信息交互需求时，其他K-1个任务（或子种群）成为任务Ta获取信息的主要来源，即:(T1，T2，…，TK) →Ta。

步骤3 信息筛选。选择所有信息来源中对自己有用的信息，过滤无用信息，可在一定程度上保证信息的正向迁移。这里根据同时处理的任务个数选择不同的信息迁移来源:

a）当K=2 时。若任务T1停滞进化，将任务T2中个体适应值快速排序，取排名前30%的个体位置作为信息迁移来源。

b）当K＞2 时。采用基于概率的信息选择模式，随机产生［0，1］的随机数rand，当rand≤时，选择任务T1作为信息迁移源，若Ta连续在λ代内不能改变进化停滞现象（即信息负迁移），则继续按概率从剩余K-2 个任务中选择信息迁移来源，如图2所示。

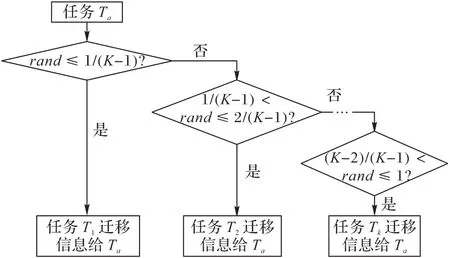
图2 多任务信息来源选择示意图Fig.2 Schematic diagram of multi-task information source selection

步骤4 信息迁移。假设t时刻，任务Ta停滞进化产生信息交互愿望，选中任务Tk作为信息迁移来源。按式（3）将任务Tk所在种群个体位置与任务Ta种群中的所有个体位置进行交叉。信息迁移不是单纯的信息增加，而是迁移信息后，种群结构的重新调整。

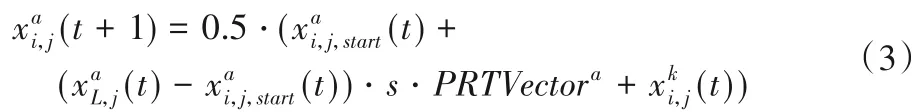
多任务SOMAMIF伪代码如下:

1） 随机产生K个子种群Pa（a∈{1，2，…，K}）用于同时处理K个极小优化问题。

2） 初始化子种群Pa(t=0)（a∈{1，2，…，K}）中个体位置和参数。

3） 计算种群Pa(t=0)领先者fbesta(t=0)。

4） while（未满足循环结束条件）

5）t=t+1；

6） for（对任意子种群Pa）

7） for（对任意个体i，i∈Pa）

8） 按式（1）～（2）更新个体i位置；

9） 计算个体i适应值；

10） end for

11） 比较得出子种群Pa当前领先者

13）counta=counta+1

14） end if

15） if（counta==γ）

16） 子种群Pa产生信息交互需求；

17） 按图2选择信息来源；

18） 按式（3）实施信息迁移，并评价个体适应值；

19）counta=0

20） end if

21） 比较子种群Pa全局极值解；

22）end for

23）end while

24）输出K个任务全局最优解。

2.3 多任务SOMAMIF复杂度分析

这里仅以同时处理2 个任务（即K=2）为例。设子种群P1和P2规模分别为m，最大迭代次数为Maxiter，任务T1维数为d1，任务T2维数为d2，假设d1＞d2，则多任务搜索空间维数为D=max{d1，d2}=d1，当计算任务T2适应值 时，取d1中 的前d2维。

2.3.1 时间复杂度分析

SOMAMIF 同时优化2 个任务的时间复杂度等于求解任务T1时间复杂度Q1和T2时间复杂度Q2之和。其中:

1）优化任务T1时间复杂度Q1分析。

a）子种群P1运行时间复杂度包括:初始化子种群P1中m个个体位置时间复杂度为O(m·d1)；初始化参数s、PRT时间复杂度为O(1)；计算个体适应值时间复杂度为O(m·d1)；比较得出当前领导者位置时间复杂度为O(m)；计算参数PRTVector时间复杂度为O(1)；更新个体迁移后位置时间复杂度为O(m·d1)；更新子种群P1领先者位置时间复杂度为O(d1)。经过Maxiter次迭代后得=O(Maxiter·m·d1)。

b）子种群P1筛选信息、P2向P1迁移信息复杂度包括:假设在整个算法Maxiter次迭代过程中，子种群P2向P1传递了θ1次信息，每次产生信息交互需求时，将子种群P2个体适应值进行快速排序时间复杂度为O(mlogm)，每次信息迁移产生新位置的时间复杂度为O(m·d1)，计算新位置适应值时间复杂度为O(m·d1)，比较得出新领导者位置时间复杂度总时间为O(m)，总体复杂度为O(θ1·m·d1)；其他操作时间复杂度常数次O(1)。综合分析，得=O(θ1·m·d1)，则Q1==O(Maxiter·m·d1)+O(θ1·m·d1)。

2）优化任务T2时间复杂度Q2分析。

优化任务T2的过程与T1相似，也包括两部分:

a）子种群P2运行时间复杂度包括:初始化子种群P2中m个个体位置时间复杂度为O(m·d1)；初始化参数s、PRT时间复杂度为O(1)；计算个体适应值时间复杂度为O(m·d2)；比较得出当前领导者位置时间复杂度为O(m)；计算参数PRTVector时间复杂度为O(1)；更新个体位置时间复杂度为O(m·d1)；更新子种群P2领先者位置时间复杂度为O(d2)。综合上述分析，因d1＞d2，经过Maxiter次迭代后得Q12=O(Maxiter·m·d1)。

b）子种群P2筛选信息、P1向P2迁移信息复杂度包括:假设在整个算法Maxiter次迭代过程中，子种群P1向P2传递了θ2次信息，每次产生信息交互需求时，将子种群P1个体适应值进行快速排序时间复杂度为O(mlogm)，每次信息迁移产生新位置的时间复杂度为O(m·d1)，计算新位置适应值时间复杂度为O(m·d2)，比较得出新领导者位置时间复杂度总时间为O(m)，总体复杂度为O(θ1·m·d1)；其他操作时间复杂度常数次O(1)。综合分析，得=O(θ2·m·d1)。则Q2==O(Maxiter·m·d1)+O(θ2·m·d1)。

因θ1＜Maxiter，θ2＜Maxiter，综 合1）和2），得 出SOMAMIF 求解两个不同优化任务的时间复杂度如式（4）所示:

2.3.2 空间复杂度分析

1）任务T1所需存储空间包括如下两部分:

a）子种群P1所需存储空间:存储子种群P1中m个个体位置所需空间为m·d1；存储P1领先者位置所需空间为d1。

b）子种群P1筛选、迁移信息所需存储空间:存储新位置所需存储空间为m·d1。

2）任务T2所需存储空间包括如下两部分:

a）子种群P2所需存储空间:存储子种群P2中m个个体位置所需空间为m·d1；存储P2领先者位置所需空间为d2。

b）子种群P2筛选、迁移信息所需存储空间:存储新位置所需存储空间为m·d1。

因d1＞d2，综合1）和2），得出SOMAMIF 求解两个不同优化任务的空间复杂度如式（5）所示:

由式（4）～（5）可知:本文多任务SOMAMIF 求解两个不同任务的时间和空间复杂度均为多项式。

将本文算法与文献［16］算法、文献［18］算法进行对比分析，设置相同迭代次数Maxiter、种群规模m、最大搜索空间维数d1。文献［16］的协同多任务粒子群优化（MultiTasking Coevolutionary Particle Swarm Optimization，MT-CPSO）算法同时处理两个不同任务时间和空间复杂度分别为O(Maxiter·m·d1)、O(m·d1)。

当种群规模m小于等于函数维数d1，即m≤d1时，文献［18］的信息交互多任务粒子群优化（Information Exchange Particle Swarm Optimization for Multitasking，IEPSOM）算法同时求解两个不同任务的时间和空间复杂度分别为O(Maxiter·m·d1)和O(m·d1)；当m＞d1时，文献［18］算法同时求解两个不同任务的时间和空间复杂度分别为O(Maxiter·m2)和O(m2)。

综合上述对比分析可知，本文多任务SOMAMIF的时间复杂度和空间复杂度与MT-CPSO算法、IEPSOM算法相当。

3 仿真实验与结果分析

3.1 SOMAMIF求解多任务高维函数优化问题

本节以8 个经典benchmark 函数优化问题为例，如式（6）～（13），按函数和维数构造不同多任务组合，在同一时刻处理3 个优化问题，以验证SOMAMIF 求解多任务性能。为强调SOMAMIF多任务环境中信息筛选机制的优异性能，这里采用消融法比较信息筛选前后算法性能差异，若信息筛选前后涉及到相同的参数，则设为一致。

为方便描述，将上述8 个函数名称进行简写，并给出函数全局最优值，如表1所示。

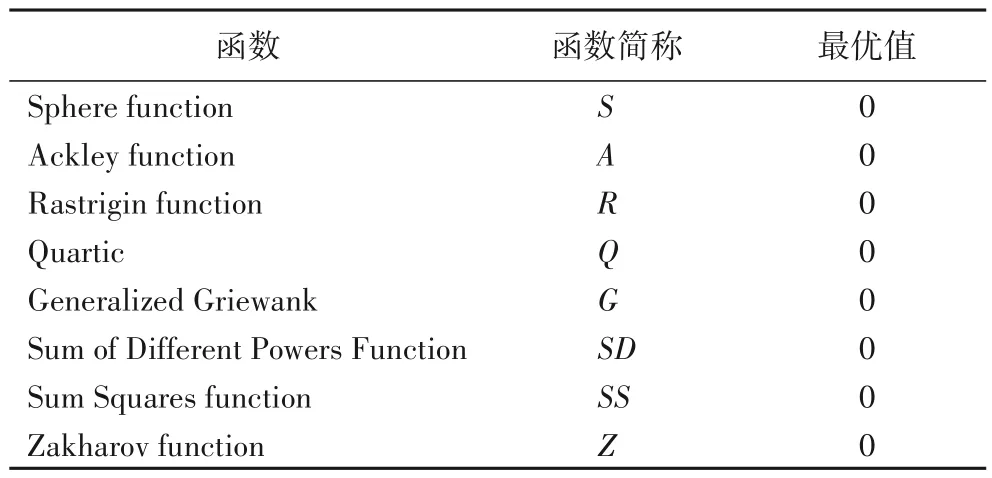
表1 函数简称及最优值Tab.1 Function abbreviation and optimal value

当SOMA 中未引入信息筛选机制处理50 维Sphere 函数优化问题时，将其标签设为50S；若采用多任务SOMAMIF 同时处理50 维Sphere function、50 维Ackley function、50 维Rastrigin function，则将其标签设为（50S，50A，50R），依此类推，将上述8个函数分成如下6个多任务组:

F1={50S，50A，50R，(50S，50A，50R)}

F2={50S，50G，50Q，(50S，50Q，50G)}

F3={50SD，50SS，50Z，(50SD，50SS，50Z)}

F4={100S，100A，100R，(100S，100A，100R)}

F5={(100S，100G，100Q，(100S，100G，100Q)}

F6={(100SD，100SS，100Z，(100SD，100SS，100Z)}

F1、F2、F3、F4、F5、F6分别用于比较在SOMA 中引入信息筛选机制前后，50S、50A、50R、50G、50Q、50SD、50SS、50Z、100S、100A、100R、100G、100Q、100SD、100SS、100Z的求解性能。

算法参数设置如下:多任务组合F1、F2、F4、F5搜索空间设为[-30，30]，F3、F6搜索空间均设为[-10，10]，子种群规模为50，迭代次数为500，步长step=0.08。同时，多任务SOMAMIF中的信息迁移节点γ=10。多任务组合F1、F2、F3、F4、F5、F6单独运行30次求平均值实验结果如表2所示。

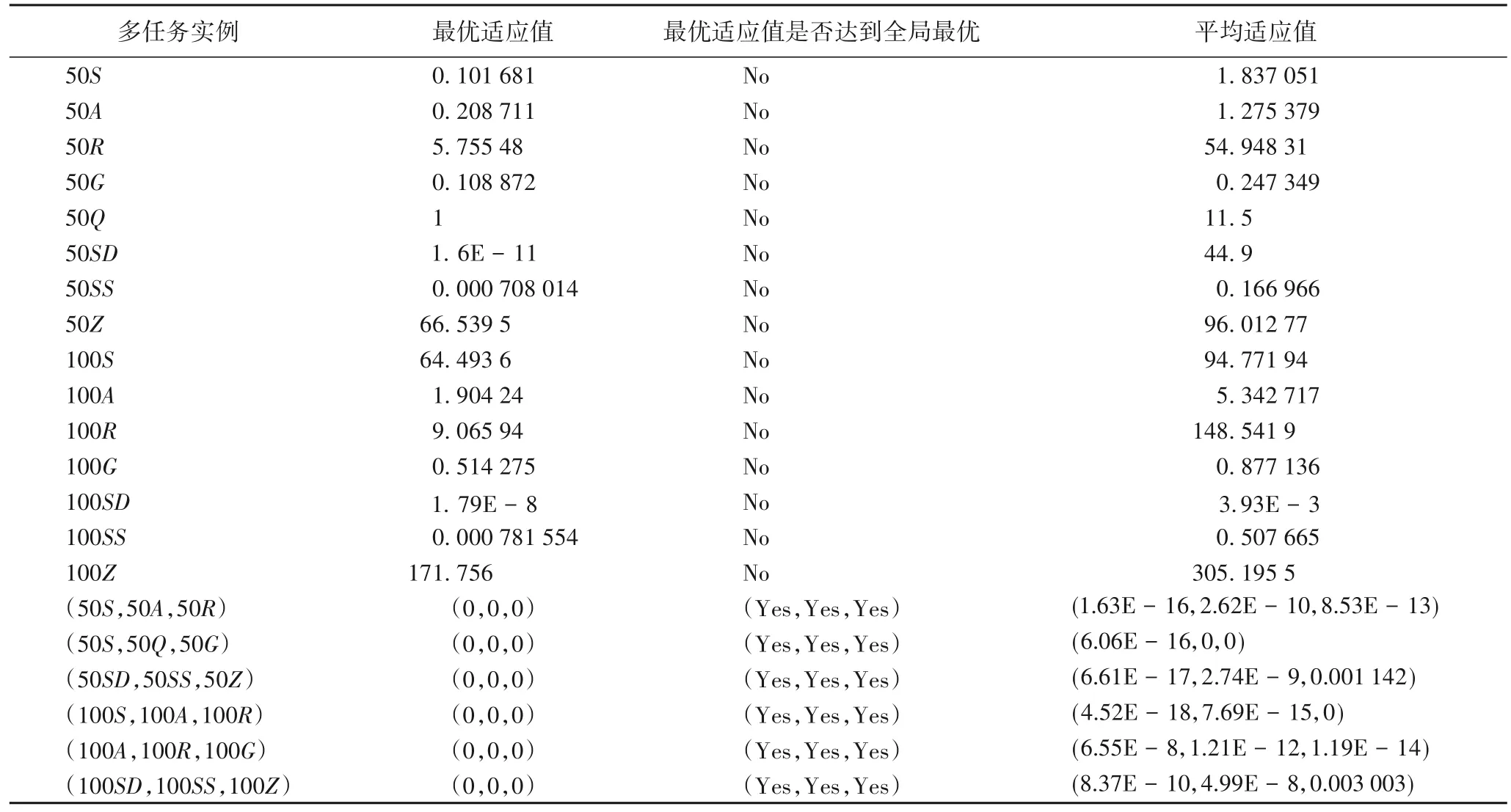
表2 引入信息筛选机制前后本文算法求解多任务高维函数优化问题的实验结果Tab.2 Experimental results of proposed algorithm solving multi-task high-dimensional function optimization problems before and after introducing information filtering mechanism

当SOMA 中未引入信息筛选机制求解50 维函数，如50S、50A、50R、50G、50Q、50SD、50SS、50Z时，最优适应值分别为0.101 681、0.208 711、5.755 48、0.108 872、1、1.6E-11、0.000 708 014、66.539 5，平均适 应值分别为1.837 051、1.275 379、54.948 31、0.247 349、11.5、44.9、0.166 966、96.012 77，而引入信息筛选机制的多任务SOMAMIF 求解任务（50S，50A，50R）、（50S，50Q，50G）、（50SD，50SS，50Z）组合时，50S、50A、50R、50Q、50G、50SD、50SS、50Z最优适应值均达到了全局极值解0，平均适应值也远远优于未引入信息筛选机制的SOMA。当上述8 个函数维数上升到100 维时，多任务SOMAMIF 所得结果也明显优于SOMA，这说明本文提出的多任务算法通过子种群之间的信息筛选和迁移能显著提高解的质量。

表3 将本文多任务SOMAMIF 运行结果与文献［16］的多任务MT-CPSO 算法、文献［18］的多任务IEPSOM 算法进行对比，本文算法和MT-CPSO算法、IEPSOM算法在求解上述50维和100 维函数时，实验结果基本相当，但本文算法在求解100R、100SS、100Z时性能优于MT-CPSO 算法，且除了求解50SD、100SD这两个函数时稍劣于IEPSOM 算法外，本文算法求解其他函数结果均优于IEPSOM 算法。这些结果在SOMAMIF 和MT-CPSO 算法、SOMAMIF 和IEPSOM 算法威 尔克森符号秩检验结果中得到了进一步证实（设置信度水平为0.05），结果如表4所示。

表3 不同算法求解多任务高维函数优化问题的平均适应值对比Tab.3 Average fitness comparison of different algorithms in solving multi-task high-dimensional function optimization problems

表4 不同算法求解多任务高维函数优化问题威尔克森符号秩检验结果Tab.4 Wilcoxon signed-rank test results of different algorithms in solving multi-task high-dimensional function optimization problems

图3 进一步给出信息筛选前后，高维函数50S、50A、50R、50Q、50G、50SD、50Z、100S、100A、100R、100G、100Z单独运行30 次的平均收敛曲线。由图3 可知，当SOMA 中未引入信息筛选机制时，上述50维或100维函数收敛速度缓慢，均停滞在局部极值解附近，而SOMAMIF能明显同时加速多个任务的收敛，使其快速收敛至全局最优解。

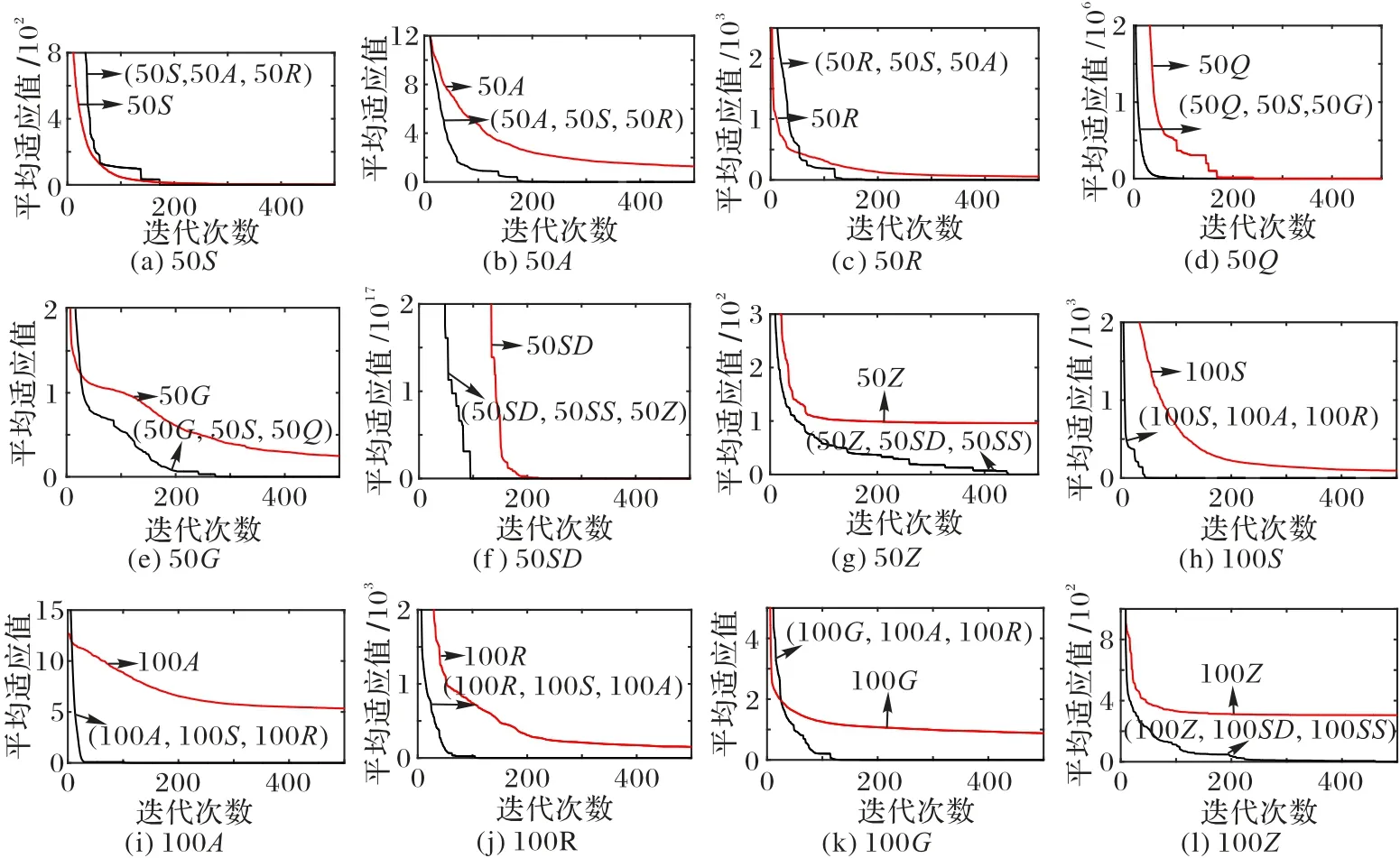
图3 信息筛选前后高维函数平均收敛曲线图Fig.3 Average convergence curves for high-dimensional functions before and afterinformation filtering

3.2 SOMAMIF结合分形维数提取学生返乡关键制约因素

2020 年一场突发疫情席卷全球，不可避免地对中国乃至世界经济造成较大冲击，企业稳岗压力增大，一些企业裁员数上升，劳动力市场需求“缩水”，失业人员增加。2020 届全国普通高校毕业生874 万，比上一年增加了40 万人，增量、增幅均为近年之最，这让原本严峻的就业形势雪上加霜。尽管地方政府出台了一系列措施，积极鼓励大学生返乡创业就业，但收效甚微。有效识别制约大学生返乡关键因素，可为地方政府鼓励和引导大学生返乡就业政策制定、调整提供科学参考依据。因影响大学生返乡因素众多，并可能存在多重共线性，冗余因素的存在不仅导致计算效率低下，还在一定程度上干扰辨识过程。

大学生返乡关键制约因素挖掘过程实质上是一个特征选择过程，属于典型的二元离散优化问题。本节以SOMAMIF为搜索策略，将种群中粒子位置通过Sigmoid 函数转换成1 或0，1或0分别表示该因素是或否被选择为返乡关键制约因素，分形维数作为子集评估度量准则，同时提取户籍所在地分别为县及以下和三线以上城市的大学生返乡关键制约因素。

目前计算数据集分形维数的方法较多，这里采用盒计数法。假设数据集指标个数为L，数据点落在边长为r的L维格子中，其关联分形维数如式（14）所示:

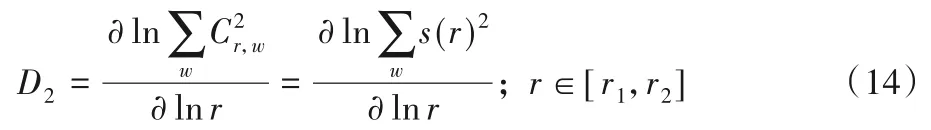
其中:s(r)=Cr，w为落入第w个格子的数据点数；r为格子半径，［r1，r2］为数据集无标度空间。数据集中数据点每维采用十进制实数表示，根据点坐标值和盒子半径统计该半径下每个盒子中落入点数的平方和，根据不同半径r得到一系列不同点对（lnr，lns(r)），拟合后所得直线斜率，即为关联分形维数。

3.2.1 数据集描述及数据预处理

仿真实验以高校学生为研究对象，将受访学生分成两组:

①户籍所在地为县及以下高校学生；

②户籍所在地为三线及以上城市高校学生。

涉及到的返乡因素共14 个，分别为:1）所在大学类型；2）学历；3）家庭情况；4）学习成绩；5）当前就业形势；6）自身求职竞争力；7）父母是否支持返乡；8）家乡薪资待遇；9）家乡生活成本；10）回乡就业优惠政策；11）家乡生活节奏工作压力；12）对家乡未来发展环境满意度；13）对家乡基础设施满意度；14）对家乡居住环境满意度。返乡意愿有两种:愿意返乡就业/不愿意返乡就业。

构建基于SOMAMIF的多任务组:

1）任务T1:挖掘户籍所在地为县及以下高校学生返乡关键制约因素。

2）任务T2:挖掘户籍所在地为三线及以上城市高校学生返乡关键制约因素；

其中任务T1实例数为383，任务T2实例数为43。

3.2.2 多任务高校学生返乡关键制约因素提取结果分析

按式（14）分别计算任务T1和T2原始数据集分形维数为2.713 13、4.185 62，然后向上取整得任务T1返乡关键制约因素个数为3（即，任务T2返乡关键制约因素个数为5（即。

将子种群规模设为50，迭代次数为20，信息迁移节点γ=3。采用本文多任务SOMAMIF结合分形维数同时求解任务T1和T2后，得到户籍所在地为县及以下高校学生返乡关键制约因素为:父母是否支持返乡、家乡薪资待遇和家乡居住环境满意度；户籍所在地为三线及以上城市高校学生返乡关键制约因素为:父母是否支持返乡、家乡薪资待遇、家乡生活成本、家乡生活节奏工作压力、对家乡基础设施满意度，约简率分别为78.57%和64.29%。

进一步采用支持向量机（Support Vector Machine，SVM）计算得出返乡关键制约因素提取前后数据集的平均分类准确率，任务T1和T2原始数据集的平均分类准确率分别为72.913 65%和82.226 18%，最优返乡关键制约因素平均分类准确率分别为73.262 31%和82.824 75%，平均分类准确率分别提高了0.348 66个百分点和0.598 57个百分点。

图4 和图5 分别给出了引入信息筛选机制前后算法单独运行30 次时，不同户籍高校学生返乡关键制约因素的平均分类准确率收敛曲线。

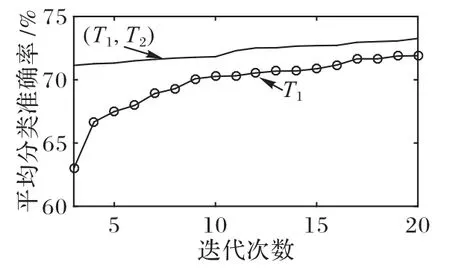
图4 信息筛选前后任务T1平均收敛曲线Fig.4 Average convergence curves for task T1 before and after information filtering

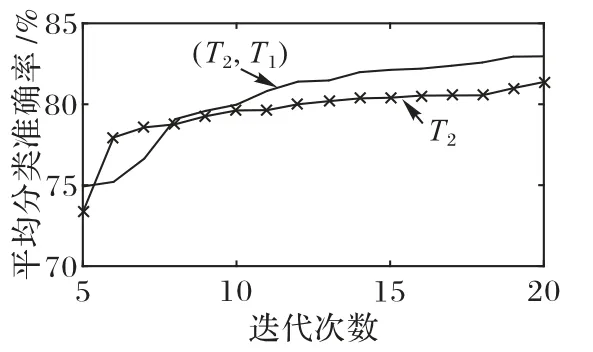
图5 信息筛选前后任务T2平均收敛曲线Fig.5 Average convergence curves for task T2 before and after information filtering

由图4～5 可知，多任务（T1，T2）的收敛速度明显优于T1和T2，能显著缩短返乡关键制约因素的提取时间。

表5 进一步给出了不同户籍高校学生返乡关键制约因素提取前后威尔克森符号秩检验结果，设置信度水平为0.05，由表5可知，T1和（T1，T2）、T2和（T2，T1）的差距显著。

表5 返乡关键制约因素提取前后威尔克森符号秩检验结果Tab.5 Wilcoxon signed-rank test results before and after key home returning constraints extraction

4 结语

本文通过挖掘自组织迁移算法的“隐并行性”，在基本SOMA 中基于信息迁移机制在同一时间内有效求解多个不同优化问题，并引入基于概率的信息选择方法，在一定程度上保证了信息的正向迁移，能显著提高多任务的求解质量并加速各优化问题的收敛，为多任务优化提供了一种新颖的高性能计算模型。本文从全新视角研究SOMA，既拓宽了SOMA 的知识内涵，也为后续研究推广到其他群智能算法实现多任务处理，奠定了理论和实验基础。