基于随机子空间的扩展隔离林算法
谢 雨,蒋 瑜,龙超奇
(成都信息工程大学软件工程学院,成都 610225)
(∗通信作者电子邮箱jiangyu@cuit.edu.cn)
0 引言
大数据时代的到来,使得海量的数据被收集和存储在数据库中,从体量巨大的数据中挖掘可理解的知识显得更加有意义。作为数据挖掘工作中重要的一环,异常检测算法正在蓬勃发展[1]。越来越多的异常点检测算法正在进一步被运用于日常生活的方方面面[2]。
近年来,国内外学者研究提出了多种异常检测算法。文献[3]中对这些算法进行了分类总结。按照异常识别技术分为:以基于角度的离群值检测(Angle-Based Outlier Detection,ABOD)算法[4]与基于连接函数的异常检测(COPula-based Outlier Detection,COPOD)算法[5]为代表的基于统计的方法;以K最近邻(K-Nearest Neighbor,KNN)分类算法[6]为代表的基于距离的方法;以局部异常因子(Local Outlier Factor,LOF)算法[7]为代表的基于密度的方法;以及以自编码器(Autoencoder)[8]为代表的基于学习的方法等。除此之外,基于集成的方法同样也在不断地被研究,其中具有代表性的技术包括:Bagging[9]与Boosting[10]抽样等。文献[11]中提出了一种基于隔离思想[12]的集成学习算法[1]:孤立森林(isolation Forest,iForest)算法,该算法首先构建了一个由多棵孤立树组成的孤立森林,随后将待检测数据点在孤立森林中进行遍历,记录该数据点被完全隔离的平均路径长度并生成对应的异常分数。文献[13]中指出由于iForest 算法的核心思想为隔离,且每棵孤立树通过随机选择的特征值来进行隔离,所以该算法具有计算速度快、准确度高与内存占用低等优点。
传统方法在各个领域内被广泛应用,可以通过不同方法的结合产生性能更优的异常检测模型。文献[14]中结合LOF算法的最近邻思想与iForest 算法的隔离思想,提出使用最近邻集合进行隔离(isolation using Nearest Neighbor Ensemble,iNNE)的异常检测算法,使用最近邻隔离超球体来隔离目标空间中的数据。该算法是一种基于隔离思想的高精度集成学习算法,具有精度高的优点,但在样本数量巨大的数据集中,时间开销太大。文献[15]中结合多粒度扫描机制,提出了基于多粒度随机超平面的孤立森林(Multi-dimensional Random Hyperplane iForest,MRHiForest)算法,该算法在多个小于原始数据空间的k维空间内分别构建孤立森林,通过多个森林集成投票机制,构成层次化集成学习的异常检测模型。该模型提高了在高维数据集上进行异常检测工作的稳定性与准确性,但存在精度下降、时间开销增加等缺点。
文献[16]中指出,iForest算法虽然效率与精度很高,但由于隔离条件通常为轴平行的,轴平行的隔离条件必然会导致隔离平面的交叉,进而产生呈规则分布的异常分数不准确区域。文献[17]中进一步指出,在高维数据空间中使用iForest算法将导致类似的异常分数不准确区域大量存在,因此将这种问题定义为“局部异常不敏感问题”,并在最后提出了扩展隔离林(Extended Isolation Forest,EIF)算法,该算法则完全解决了孤立森林算法对局部异常不敏感的问题。但由于EIF 算法在扩展孤立树的每一个节点上进行隔离计算时,都需要进行一次向量点乘运算,所以在预测中高维数据时,其时间开销往往远大于iForest算法。
综上所述,iForest 算法对局部异常不敏感的问题会导致部分异常点无法被准确检测,而EIF 算法虽然解决了局部异常不敏感的问题,但由于该算法的时间开销太大,在高速发展的当下并不适用。
因此,本文结合子空间思想提出了基于随机子空间的扩展隔离林(Extended Isolation Forest based on Random Subspace,RS-EIF)算法。该算法从数据空间中随机选择维度构建子空间,并使用随机超平面来避免轴平行隔离条件下隔离条件重合区域的产生。本文算法在解决iForest算法对局部异常不敏感问题的同时,相较于EIF算法减少了计算开销。
1 相关工作
1.1 iForest算法
1.1.1 孤立森林的构建
设数据集D={d1,d2,…,dn}且D⊂Ru,其中Ru为实数集,u为最高维度,n为数据个数,di={xi1,xi2,…,xiu},其中i∈[0,n]。
文献[12]定义孤立森林的构建过程为:首先,在数据集D中随机抽取η次,每次确定ψ个样本作为训练集;然后,在每次抽样完成后,以lbψ为高度限制构建一棵孤立树;最后,在构建η棵孤立树后,集成为一个孤立森林。
在每一个孤立森林中,包含的孤立树均为二叉树结构,下面给出孤立树的定义。
定义1孤立树。从[1,u]中随机确定一个整数p作为随机选择的维度,统计维度p的范围[pmin,pmax],并在该范围下随机确定隔离条件q。当训练集ψ中的数据点在p维度的值小于q时,将该数据确定为节点的左子树节点;反之确定为右子树节点。递归构建一棵高度限制为lbψ的二叉搜索树。
完成构建孤立森林后,得到一个基于树形结构的集成学习模型[18]。
1.1.2 孤立森林的缺点
在孤立森林中,数据点的异常程度通常由数据点在每棵孤立树中遍历的深度决定。这里的深度指的是数据点在空间中被划分到无法继续划分的子空间时所需的划分次数h。使用数据dk在具有η棵孤立树的孤立森林中进行遍历,得到路径深度集合H(dk)={h1,h2,…,hη},并求得平均深度E(h)。最后,将平均深度值通过式(1)归一化处理为一个取值范围为0~1的异常分数s(dk,n)。

式中,c(n)为归一化因子,被定义为搜索失败的平均路径[12]。式(2)为c(n)的具体计算方式:
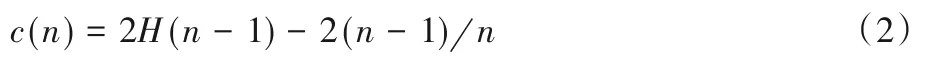
其中,H(i)为调和级数,可以通过ln(i)+0.577 215 664 9(欧拉常数)确定。
数据并不只是单一地分布在一个聚类中心,真实的数据往往具有多个聚类中心[19]。由于iForest算法的隔离条件是轴平行的,在多元数据集中,算法会因隔离条件的重叠使得局部异常难以被检测到,从而导致算法精度下降。针对该问题,提出了基于随机斜率构建超平面的EIF算法[17]。
1.2 EIF算法
1.2.1 EIF算法相关定义
EIF 算法基于iForest 算法进行改进,将轴平行的隔离条件替换为具有随机斜率[20]的超平面。
定义2随机斜率。在二维空间中,随机超平面可以理解为线,而线段是具有斜率的,其斜率可以用平面内随机一个点到原点的向量表示。同理,在k维的高维空间中,其随机斜率可以表示为空间内的向量j=(i1,i2,…,ik),其中i∈[0,1)且随机生成。
本文将一个N维空间定义为一个具有N条坐标轴的空间。若存在一个超平面与N条坐标轴中的一条相交,则称该超平面的扩展程度为0。以二维空间为例,在二维空间中,当扩展等级为0 时,隔离超平面可以理解为一条平行于坐标轴的直线。由于超平面需要由斜率与截距确定,下面给出自定义隔离等级的随机截距向量与隔离超平面的定义。
定义3自定义隔离等级的随机截距向量。在维度为k的空间中,存在s=(n1,n2,…,nk),当隔离等级为k-1 时,n1,n2,…,nk均为不为0的实数。
定义4隔离超平面。在EIF 算法中,通过随机生成超平面的随机斜率j与具有自定义隔离等级的存在于超平面上的随机截距s可以确定一个唯一的隔离超平面。
在确定隔离超平面后,隔离条件确定为:(d-s)·j,其中d表示来自数据集D中的一个待检测数据点。当隔离条件的值小于0 时,将d划分到当前根节点的左子树,反之划分到当前节点的右子树。
1.2.2 EIF算法的优势
为了展示由于隔离平面轴平行导致的精度下降的问题,本节首先使用基于正弦函数分布的二维数据集来计算各个点的异常分数,并使用热图分别绘制EIF 算法与iForest 算法对该数据集进行分析后的得分分布。实验数据集为随机在正弦曲线两侧呈高斯分布的1 000个二维数据点。随后,对所得的数据分别使用EIF 算法与iForest 算法进行预测后,将所得到的异常分数划分为10 个不同的等级,为每个等级标注边界,并使用热图绘制边界。两种算法的得分热图如图1所示。
iForest 算法得分热图如图1(a)所示,而EIF 算法得分热图则如图1(b)所示。对比两个图可以发现,正弦函数的任意两个波峰或波谷之间,EIF 算法计算得到的异常分数相较于iForest 算法异常分数更加具有层次感;而且在EIF 算法的得分热图中,在数据分布外并没有存在矩形的得分异常区域。因此,EIF 算法可以更好地计算处在正弦函数任意两个波峰或波谷之间局部数据点的异常得分。

图1 正弦分布数据上不同算法得分热图Fig.1 Score heat maps of different algorithms on sine distribution data
1.2.3 EIF算法的劣势
EIF 算法核心为使用随机隔离超平面进行隔离。假设使用维度为k的数据集构建一个包含η棵孤立树的扩展隔离林,其中,每棵树均为平衡二叉树且包含有256 个节点,每棵树的扩展等级均设定为k-1。现存在随机生成的数据点m=(x1,x2,…,xk),要想计算出该点的异常分数,在iForest 森林中,最多只需要进行8η次、最少仅需要η次比较运算即可得出数据点m的遍历深度。
在EIF 森林中,每个节点上需要进行1 次向量减法与1 次向量乘法运算(在k维数据集中,需要进行k次减法、k次加法与k次乘法运算),即:最多需要8η次、最少η次向量运算。虽然在EIF 算法中的计算时间总体是呈线性增长的[16],但相较于iForest算法,EIF算法的时间成本过高。
2 RS-EIF算法
首先,引入子空间思想,在介绍子空间思想在EIF 算法中的应用后,结合集成学习的优点,使用随机子空间思想完成算法改进。然后,分析改进后算法RS-EIF 的时间复杂度与空间复杂度。
2.1 随机子空间优化
根据多粒度思想[15],本文将子空间定义为维度小于目标空间并存在于目标空间中的一个空间,此处的目标空间被定义为数据集所在的高维空间[21]。由此可知,扩展等级为k-1的EIF 算法可以理解为在维度为k-1 的子空间中构建维度为k的随机斜率向量与随机截距向量,其中k为目标空间维度。因此,EIF 算法可以理解为在一个完整的数据空间中,以子空间思想对数据进行隔离。
在文献[17]中,随着EIF 算法扩展等级的提高,算法对局部异常的敏感性也随之提升。因此,为了在实验中获得最高的精确度,扩展等级往往需要设置为k-1。
然而,在最高扩展等级的子空间中构建扩展隔离森林虽然可以得到一个高精度的异常检测模型,但是随之而来的是大量上升的运算成本。因此考虑在更小的子空间中构建扩展隔离森林来提高运算速度。
EIF 算法本身是一种集成学习算法,并包含多个弱分类器。在EIF 算法中,虽然一棵扩展隔离树的预测结果并不令人满意,但在组合多棵树构成森林后,其预测结果变得优于多数传统的异常检测算法。
因此,本文在随机子空间l中生成具有扩展等级的随机斜率j'与随机截距向量s',其中l<k。再将隔离条件优化为d·j'<s'·j'来确定数据点是否存在于l维子空间中的隔离超平面内。由此方法构建的树结构命名为随机扩展隔离树RS-Tree(Random Subspace Tree)。
由于RS-Tree的精度会低于原本的扩展隔离树,因此再通过构建多棵基于随机子空间的RS-Tree 组成一个完整的模型来提高算法的精度。下面,给出构建RS-EIF 森林的伪代码如算法1所示。
算法1 rsForest(X,t,ψ,k,extendlevel)。
输入 数据集X,树的棵数t,每棵树包含的节点个数ψ,随机子空间维度k,树的扩展等级extendlevel;
输出 包含t棵RS-Tree的RS-EIF森林。

算法1 需要构建RS-EIF 森林,该过程与EIF 算法中的扩展隔离树构建过程类似。而森林中是包含多棵树的,因此给出树的构建伪代码如算法2所示。
算法2 rsTree(X,e,l,k,extendlevel)。
输入 数据集X,当前树的高度e,树的高度限制l,子空间维度k,树的扩展等级extendlevel;
输出 1棵RS-Tree。

在一个完整的RS-EIF 森林中,要想实现对数据的决策判断,需要将该数据在森林中的每棵树进行遍历,计算其平均路径长度,最终给出判断结果。下面给出计算遍历深度的伪代码如算法3所示。
算法3 PathCount(d,tree,e,k)。
输入 数据点d,RS-Tree 的节点tree,当前路径长度e,随机子空间维度k;
输出 数据点d的路径遍历长度。

最终,在计算出目标数据点的平均路径长度(平均深度)后,再使用式(1)处理为对应的异常分数。异常分数越高,则数据的异常程度就越高。
2.2 时间与空间开销分析
2.2.1 时间开销分析
假设在n个维度为K的数据集中,构建包含t棵RS-Tree的RS-EIF 森林,每棵树包含ψ个节点,取子空间大小为k,扩展等级为k-1。其中,0 <k<K。
在训练阶段,需要进行t次随机抽样。由于t是常数,因此其时间复杂度为O(1)。在构建RS-Tree时,每棵树只需要进行一次随机的k维选择即可确定子空间,再在子空间中进行ψ次随机生成所需的两个向量并计算不同节点隔离值的工作。因此,一棵完全的RS-Tree只需要常数时间O(ψ)即可完成构建。对于包含t棵树的RS-EIF 森林,其训练过程时间复杂度为O(ψt)。
在测试阶段,一棵完全RS-Tree 中,最多只需要8 次向量乘法运算与比较运算,由于k维常量,可以近似地等于O(1)。则在t棵RS-Tree进行遍历,时间复杂度为O(t)。因此,训练阶段的时间复杂度取决于样本个数。对于n个样本,时间复杂度则等同于O(tn)。由于t是一个需要指定的参数,该参数通常为常数,因此时间复杂度可以理解为O(n)。
2.2.2 空间开销分析
由于RS-EIF 算法的目的是生成一个强分类器用于判断输入信息是否是异常的,因此,算法只需要存储这个包含t棵RS-Tree 的数据结构以及其包含的信息。因此空间复杂度为常数。
3 实验与结果分析
为了验证RS-EIF 算法的有效性,本文使用3 组实验来分别验证该算法的准确性与时间提升。
实验中,使用的人工数据集共有7 个,这些人工数据集均使用Python 自带的sklearn 包生成,每个数据所包含的数据点都是呈高斯分布均匀地分布在4 个聚类中心周围。其中,DS_One、DS_Two、DS_Three 与DS_Four 均为二维数据,其样本数量以2 000 的步长递增;而DS_Five、DS_Six 与DS_Seven 则为包含4 000 个样本的数据集,并且其维度以步长2 增长。在这些数据集中,异常数据由均匀分布在其他聚类中心周围的10个数据代替,具体的信息如表1所示。
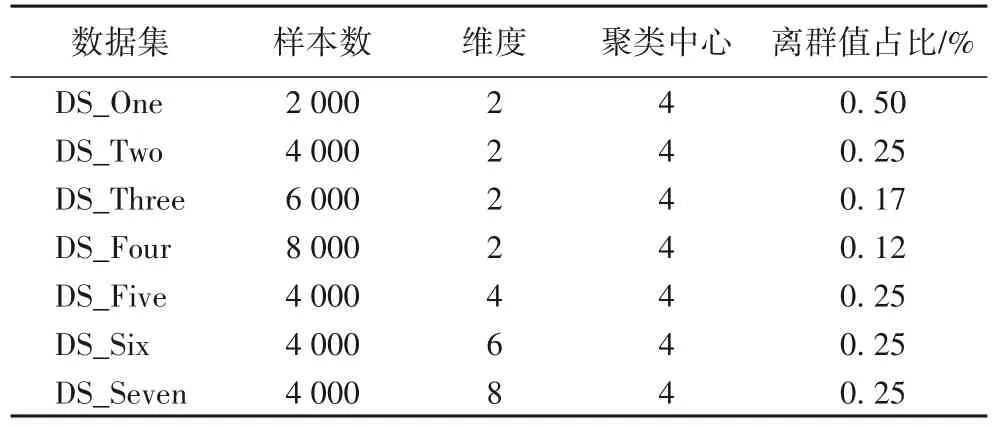
表1 实验使用的人工数据集Tab.1 Synthetic datasets used in experiments
其次,实验使用的真实数据集来自离群值检测数据库(Outliter Detection DataSet,ODDS)[22],本文选择其中9个具有代表性的多维点数据集进行实验。选取的数据集信息如表2所示。这些数据包括低维到高维、低样本数量到高样本数量的数据,可以更好地展现本文算法的性能。
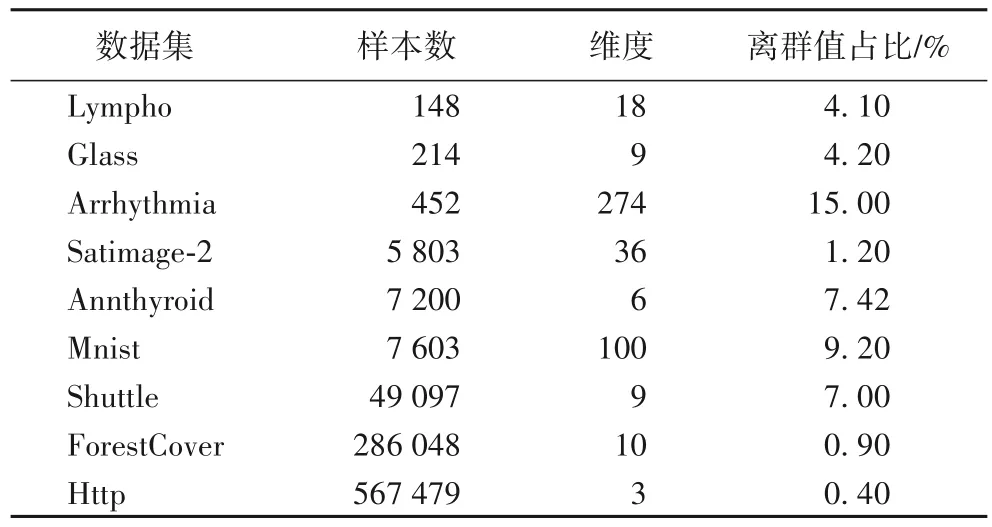
表2 实验使用的ODDS数据集Tab.2 ODDS datasets used in experiments
最后,所有实验使用Python3.8.3 编程实现,运行在Windows 10 操作系统,12 GB 内存,Intel Core i5-4200H CPU@2.90 GHz的计算机平台上。由于实验中所涉及的5种算法中有3 种均为基于树型结构的集成学习算法,因此为了更加清晰直接地展现对比结果,将3 种算法的部分参数默认设置为训练100棵包含256个节点的树。
3.1 局部异常检测
本节选取DS_One 为实验数据集。在该数据集中,存在2个聚类中心的距离偏近,因此视觉上产生了类似于存在3 个聚类中心的效果。而异常点则明显远离数据集中的大量数据。
根据前文分析,如果在该数据集上使用传统的iForest 算法,则必定会产生至少一个矩形的得分异常区域。因此,本节使用与前文类似的方式绘制EIF算法与RS-EIF算法的异常得分热图来观察是否有效避免了矩形异常区域的产生。
在参数设置方面,由于DS_One 是一个二维数据集,为了避免RS-EIF算法在维度为1的子空间出现隔离条件失效的问题,本节将子空间的维度设置为2。除此之外,两种算法的扩展等级均设置为最高等级。实验结果如图2所示。
在图2(a)中清晰地展示出:EIF 算法的异常分数热图中,并没有存在呈矩形、由隔离条件重叠所导致的分数异常区域。在图2(b)中,同样没有发现类似的矩形区域。然而,图2(b)的异常分数轮廓的平滑程度并没有达到图2(a)的程度。分析后发现,导致该现象出现的原因在于:本节并没有刻意地调整参数设置以达到最佳效果。
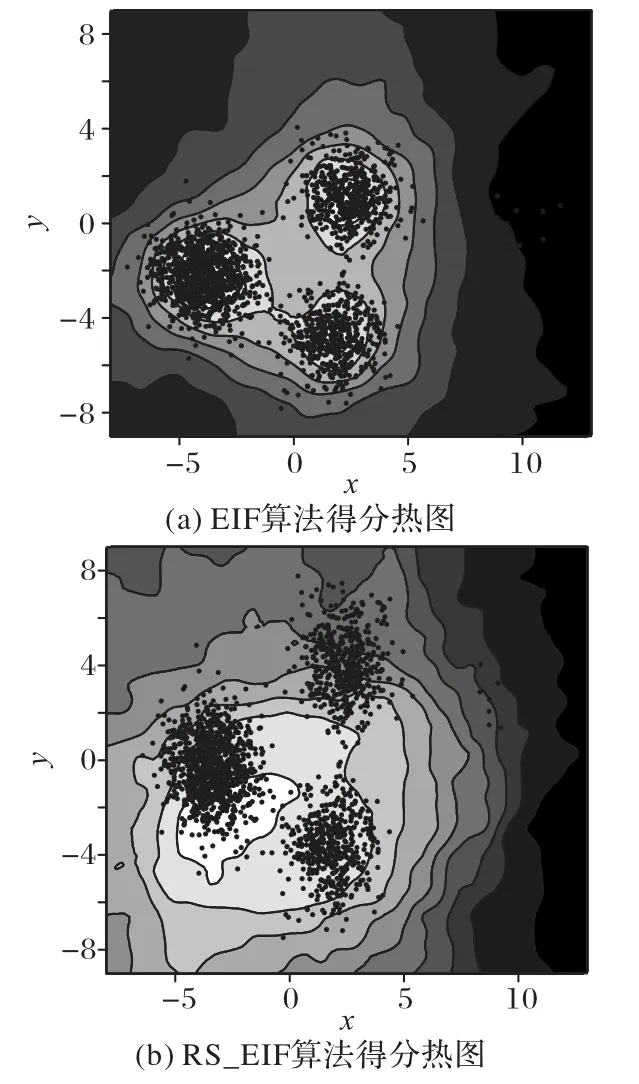
图2 多元分布数据上不同算法得分热图Fig.2 Score heat maps of different algorithms on multivariate distribution data
综上所述,不难发现,RS-EIF 算法具有与EIF 算法相似的局部异常检测能力。
3.2 维度与样本数量对算法运行时间的影响
本节首先使用RS-EIF 算法与EIF 算法对DS_One、DS_Two、DS_Three 与DS_Four 这4 个数据集进行预测。除了默认参数外,同样指定RS-EIF 算法在维度为2 的子空间进行训练,两种算法的扩展等级均设置为最高等级,并且采取10次实验求平均值的方法,得到在不同人工数据集的运行时间,实验结果如图3所示。
图3 展示了在不同样本数据量的情况下,两种算法在运行时间方面的差异。在图3(a)中,所绘制的两条线分别代表两种算法在不同数据集的运行时间。不难看出,虽然两条折线都是近似线性增加的,但RS-EIF 算法的运算时间明显少于EIF 算法。出现该现象的原因是:RS-EIF 算法在预测阶段,每个节点的遍历只需要计算1 次随机斜率向量与数据点的点乘;而EIF 算法在预测阶段的节点遍历则需要分别计算随机截距向量与数据点同随机斜率向量的点乘。
除此之外,本节还选取了DS_Two、DS_Five、DS_Six 与DS_Seven 数据比较数据维度对两种算法运行时间的影响。由于上述4 个数据的维度是不同的,因此在两种算法中,扩展等级均设置为最高等级。而RS-EIF 算法的子空间维度则分别设置为:2、3、5、7。
通过图3(b)发现,两种算法在不同维度的数据集中,运行时间均在一个固定范围内上下变化,但RS-EIF 算法的运行时间同样远少于EIF 算法。出现该现象的原因在于:所选取的数据集样本数量并不大,没有完全体现算法在不同维度数据集上的运行时间差异。
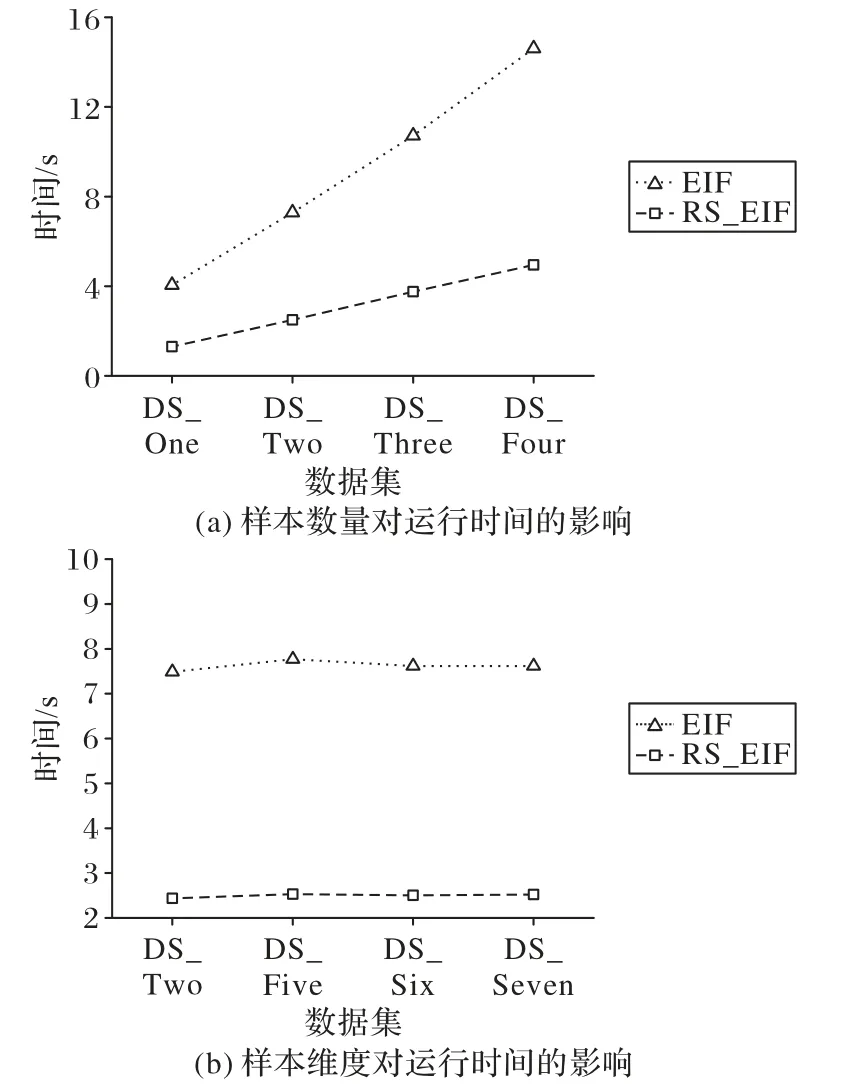
图3 数量与维度对运行时间的影响Fig.3 Impact of quantity and dimension on running time
综上所述,在相同维度的数据集中,虽然EIF 算法与RSEIF 算法时间开销均表现为随样本数量的增加而线性增加;但在样本数量相同的数据集中,EIF 算法的时间开销是远多于RS-EIF算法。
3.3 与其他异常检测算法的比较
本节将两个样本数量较多的数据集ForestCover与Http按照1∶9 划分为测试集与训练集;将两个样本数量过少的数据集Glass 与Lympho 采用10 折交叉验证求均值的方法进行实验;其余数据则使用5折交叉验证取平均值的方法获得结果。
算法选择方面,将RS-EIF 算法与同为集成模型的iForest算法、EIF 算法与轻型在线异常检测(Lightweight On-line Detection of Anomalies,LODA)算法[23]以及基于统计的COPOD 算法[5]进行对比,这些模型均使用PyOD 库[24]实现。参数设置方面,iForest 算法使用默认参数;而EIF 算法与RSEIF 算法的扩展等级则均设置为最高;除此之外,为了方便计算,RS-EIF 算法的子空间维度设置为对应数据空间维度的一半;LODA 算法的直方图数量与随机消减数则分别设置为文献[23]中提出的10与100。
表3 给出了5 种算法在时间开销与精确度方面的差异。其中:时间是指从开始训练到结束预测的时间;精确度(ACcuracy score,AC)则表示使用sklearn 包中的相应函数计算5种算法预测结果的准确度。通过表3可以发现,在样本数量大于1 000 的数据集中,RS-EIF 算法、EIF 算法的精确度与iForest 算法、LODA 算法、COPOD 算法相比分别高出了2~12 个百分点与3~15 个百分点,但在时间开销上,两种算法则均劣于其他3 种算法。除此之外,RS-EIF 算法与EIF 算法在这些数据集上的精确度均相差不超过5 个百分点,而RS-EIF 算法的运行时间却远少于EIF 算法。RS-EIF 算法与EIF 算法的精确度远高于其他算法的原因是两种算法均使用随机超平面进行隔离,可以有效识别出绝大部分异常点。因此,RS-EIF 算法相较于EIF 算法的改进是行之有效的。而在两个样本数量过少的数据中,RS-EIF 算法的精确度虽然低于EIF 算法,但与其他3 种算法对比可以发现,其精确度还是明显高于iForest 算法的,导致出现该现象的原因则可能是样本数量过少。
综合分析实验结果可知,RS-EIF 算法的时间开销在各类型的数据集上均少于EIF 算法,具体约下降60%。在实验精确度上,RS-EIF算法与EIF算法相差不大,但在中大型数据集中却明显优于iForest 算法、LODA 算法与COPOD 算法。除此之外,由于RS-EIF 算法需要在子空间中进行训练与预测,而该过程包含大量的随机运算,因此,即使集成学习的方式提高了RS-EIF 算法的精确度,但在少数数据集上,RS-EIF 算法与EIF算法相比还是略有不足。
4 结语
本文从iForest算法的隔离条件轴平行导致算法对局部异常不敏感入手,借鉴EIF 算法解决该问题的思想,提出在随机子空间中使用随机超平面进行隔离的RS-EIF 算法。该算法从减少向量计算维度的角度入手,充分利用随机的不确定性与集成学习提高弱分类器分类效果的特质,使得性能更加稳定。
实验结果验证了RS-EIF 算法存在精度高、时间开销呈线性增加并且明显少于EIF 算法的特点。在真实的ODDS 数据集上,将RS-EIF 算法与其他4 种算法分别对比了精确度与时间开销的差异,得出结论为:在样本数量更大的数据集中,RSEIF算法的精确度与EIF算法相近,但相较iForest算法、LODA算法与COPOD算法来说,RS-EIF算法的精确度平均提升约为5个百分点;在时间开销方面,该算法较EIF 算法减少约60%,但与其他3 种算法相比,时间开销并不占优势。因此,本文所提RS-EIF 算法是一种适用于中大型多元数据集的高精度异常检测算法。
由于本文算法在计算随机超平面时离不开向量的点乘计算,因此时间开销还是偏大。下一步,可以结合集成学习中,各个弱分类器之间可以不存在耦合关系的特点,将该算法部署在分布式系统上,通过合理的任务规划,提高本文算法的运行速度与精确度。

