面向动态负载的集群容器部署方法

尹 飞，龙玲莉，孔 峥，邵 涵，李 鑫，钱柱中

（1.江苏方天电力技术有限公司，南京 211102；2.南京大学计算机科学与技术系，南京 210023；3.南京航空航天大学计算机科学与技术学院，南京 211106）

（∗通信作者电子邮箱lics@nuaa.edu.cn）

0 引言

数据中心与集群以云计算的形式，根据用户动态的资源需求变化，“按需式”地为其提供可配置的资源获取服务，以实现索取资源的弹性伸缩，涵盖了传统的基础设施即服务（Infrastructure as a Service，IaaS）［1］、平台即服务（Platform as a Service，PaaS）［2］与新兴的无服务计算［3］等。这些服务模型的支撑在于基于容器化［4］的资源管理技术，以容器为上层应用提供相互隔离的计算资源。

为了应对大规模用户的访问请求，同种应用功能的多个运行实例往往被各自独立地部署于预先创建的容器之中［5］。继而，为了提升宿主机（承载容器的物理机）资源利用率，同时降低多个容器实例间的通信开销，容器会被整合到少量宿主机之上［6-7］。这样“紧致”的部署，能够在满足应用服务的同时，极大提升集群的资源利用率。

不仅如此，在运行过程中，应用的负载往往是动态变化的，文献［8-10］表明集群内各类应用的请求访问量在时间上的分布不均，如:淘宝在“双十一”期间的访问量会剧增；假期时社交网站的照片分享量会极大超出平时的均值水平；新闻事件也会使得应用的浏览量产生大幅度的波动。为此，集群更需要根据应用的负载变化，动态调整容器的资源配置，以满足应用业务的服务质量。

然而，为了整合宿主机资源［11-15］，现有的工作主要从按需式、被动式［16-18］的容器迁移入手。一方面，已有工作探讨了在宿主机上进行共享资源使用过程中，容器之间产生的资源干扰［9，19］；另一方面，一些研究在结合了共享资源使用特点［8，20］的基础上，进行容器整合的策略制定，提升宿主机的资源利用率。虽然也有工作通过预测及刻画应用各异的资源需求［21-22］，帮助容器进行更好的整合，但这些工作均带有较强的输入分布假设。

即使现有的容器化技术已经能较好地支持“应对式”的资源弹性伸缩和配置，但是对于动态负载来说，在线化的配置需求增加了作出合理容器部署的难度。一个简单的例子是，短期内“近乎完美”的容器整合可能造成未来更多容器热迁移。也就是，当容器负载过高而宿主机没有空闲资源进行拓展时，容器不得不采取热迁移的方式，将实例转移至其他空闲服务器。随之而来，热迁移不仅消耗大量计算与网络资源［23］，也会增加应用响应时间，对服务质量产生较大的影响。

结合针对集群负载的长期观察，容器的资源需求往往是此消彼长。如果能将这些此消彼长的容器整合在一台宿主机上，那么容器将会以较小的概率同时具有资源扩展需求。因此，只需为每一台宿主机预留少量资源，即可避免后续大部分的容器热迁移。然而，如何将合适的容器整合宿主机上，并确定合适的资源预留量是关键，其直接影响了宿主机的资源利用率与容器的服务质量。

虽然容器的资源需求量在不断变化，但是在弹性资源伸缩的时候，其申请增加或是释放的资源量往往具有最小的变化单位，如一个CPU 核、1 GB 内存等。相较于传统“非忙即闲”的资源模型，有限的资源使用状态及其间的变化关系更能作为细粒度描述容器资源动态变化的依据。例如，聊天应用包含有文字、语音等多种媒介，以至于信息传输负载的呈现也仅在这几个状态间切换。

为此，本文首先以细粒度的方式刻画容器的动态资源变化，即用马尔可夫链中的状态和状态间的转移，对应建模容器可能的资源需求量和不同资源需求量之间的切换。图1 展示了一个具有3 种资源需求状态的容器示例。然后，本文在基于资源预留的基础上提出面向动态负载的容器部署问题，以在限定动态迁移概率的约束下，最小化宿主机的使用数量。本文提出了面向动态负载的容器部署策略，并通过估计容器资源需求，提高部署效率。大规模基于国产软硬件的实验结果表明，所提出的部署策略能在提高宿主机资源利用率和减少容器动态迁移次数间取得平衡，在长效时间上以至多26 台宿主机的增加换取至多7次容器迁移。

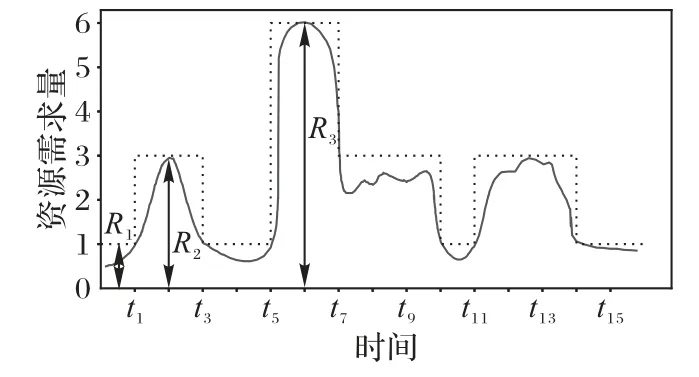
图1 容器随时间变化的资源需求Fig.1 Resource demand of dockers varying with time

本文的主要工作有:1）用马尔可夫链建模容器的多状态资源需求变化；2）提出面向多状态负载的容器部署策略，利用资源需求量的估计值提高部署效率；3）进行大量实验，通过与其他部署策略比较，评估本文所提出的部署策略的性能。

1 相关工作

1.1 虚拟机/容器负载刻画

动态负载的变化是虚拟机/容器部署过程不可忽视的特征。由于容器是轻量级的虚拟机，因此，本文只考虑针对容器的相关部署与应用。文献［8］统计了Google 集群中不同资源的利用率以及各自对应的总时间占比，表明了资源需求变化的动态性和可描述性；文献［19］研究了负载激增的模式，提出有关激增负载测试的方法；文献［9］调研了资源需求量波动对服务质量的影响；文献［20］优化了数据中心与集群针对容器负载变化而产生的重配置资源的开销。上述工作对资源配置的某方面开展了研究，但未考虑合理调整资源利用的方式。

近期工作主要致力于把变化的负载建模成为随机变量，即非确定量。文献［21］提供了在资源需求量服从特定随机分布下的近似算法；文献［22］主要研究了资源需求服从正态分布的情况；文献［14-15］提出针对资源需求量服从高斯分布的近似算法。这些相关方法可以提供一定的资源需求描述能力，但难以支撑容器部署的稳定性要求，易引发容器迁移。

然而针对服从特定概率分布的资源需求量而设计的算法不具有普遍性。虽然文献［24］把激增的资源需求量建模为二状态马尔可夫链，但该算法对资源需求量的状态数等有较大限制。

1.2 虚拟机/容器整合与迁移

作为提高资源利用率的重要方式，虚拟机/容器整合［11，25］已被学术界和工业界广泛地研究与认可。工业界代表性的产品有VMware 分布式资源调度［12］和IBM（International Business Machine）服务工具［13］。大多数研究把这个问题视作:在服务器容量、服务等级协议等限制条件下最小化所使用的物理服务器数量。这些工作均将容器资源需求量表示为定值，使用一系列类似装箱的启发式策略，如降序首次适应（First Fit Decreasing，FFD）［6］、随机装箱等［14-15］，却无法应对集群环境中动态的容器资源变化需求。

当宿主机资源无法满足容器资源扩张需求时，容器热迁移随即进行。文献［16］以同时最小化迁移传输能耗及容器服务时延作为目标；文献［17］旨在设计具有时延保障的热迁移策略；另有文献［18］考虑集群间利用传输控制协议（Transmission Control Protocol，TCP）的路径多样性进行热迁移。但这类工作往往是被动地进行容器的调整，没有在长效时间维度上进行容器整合与迁移的优化。

针对上述工作的局限，本文使用多状态马尔可夫链为容器的资源需求量变化进行建模，以设计有效的面向动态负载的容器部署策略。

2 系统模型

2.1 场景定义

集群有大量的物理机，通过在物理机（宿主机）上部署容器来向用户提供服务。如图2 所示，容器与宿主机的关系由部署策略决定。

图2 容器部署示意图Fig.2 Schematic diagram of docker deployment

一方面，尽管用户通常会声明容器的最大资源需求量，但由于物理机的购置成本、维护成本和运行成本都较高，总是为每个容器预留足够的计算资源在经济上是不合理的。运营者总是希望尽可能减少宿主机的占用量。另一方面，若没有为容器预留一定的计算资源，当其资源需求量发生变化时，集群必须通过动态迁移来保证容器的性能不受影响，由此会带来较大的迁移代价。基于这两点考虑，本文旨在为集群设计一种容器部署策略，使得宿主机资源利用率较高、数量较少，同时把容器动态迁移次数控制在较小的范围内。

2.2 单容器资源需求模型

容器资源需求量是动态变化的，能被量化为多个状态（如图1 所示）。本文将该特性称为容器的多状态特性，并用多状态的马尔可夫链进行建模，如图3所示。假设集群共创建了n台容器，并考虑第k台容器。用Nk表示第k台容器的状态总数，并令R(k)=(R1(k)，R2(k)，…，，其中Ri(k)表示第k台容器中状态i的资源需求大小。本文用Pij(k)表示第k台容器中状态i到状态j的转移概率，那么这些参数所构成的是这台容器的状态转移概率矩阵。本文用Sij(k)表示第k台容器在两个连续时间段从状态i转换到状态j的次数，那么有Pij(k)=以图1 所示为例，分别用R1(k)、R2(k)、R3(k)表示由少到多的三种资源需求量，则S11(k)=2，S12(k)=2，S13(k)=1，且能计 算转移 概率为P11(k)=0.4，P12(k)=0.4，P13(k)=0.2。

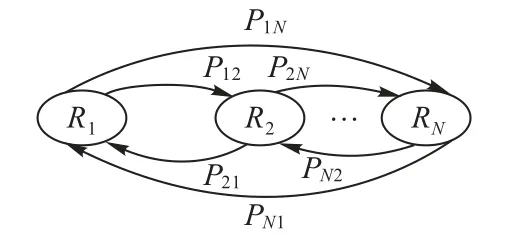
图3 基于马尔可夫链的容器资源状态模型Fig.3 Markov chain based resource state model for docker

一般来说，上述描述的马尔可夫链通常是非周期不可约的，因为实际应用中任两个状态都有可能相互切换。而任何状态都可能在下一刻保持不变，故存在有平稳状态的分布，即μ(k)=(μ1(k)，μ2(k)，…有:

因此，容器k的描述可由其资源需求量R(k)和平稳分布μ(k) 组成，构成的是2×n维矩阵，定义为V(k)=[R(k)，μ(k)]T，1 ≤k≤n。

2.3 多容器的复合资源需求模型

对于n台容器来说，每个V(k)有Nk种状态，每台容器的状态变化相互独立。因此，这n台容器一共有N=种状态。用S(k)表示容器V(k)当前的所有状态，则这n台容器在当前的复合状态可以用S=(S(1)，S(2)，…，S(n))来表示。那么，从状态S转移到S'=(S(1)'，S(2)'，…，S(n)')的概率为:

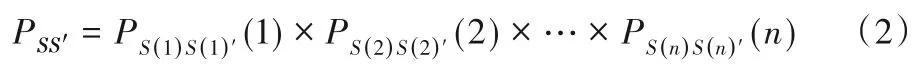
这里需要说明，本文将总共N种状态用1～N进行标号。更进一步，对于当前所处的状态(S(1)，S(2)，…，S(n))，本文用i1表示S(1)，i2表示S(2)，以此类推。从而有状态转移矩阵P=[Pij]N×N。这个马尔可夫链通常也是无周期不可约，故存在唯一的可达的平稳分布:

根据2.2 节所述，容器V(k)的平稳分布定义为μ(k)=(μ1(k)，μ2(k)，…，μNk(k))。则π和μ(k)的关系如定理所述。

定理1令有π=π'，即n台容器平稳处于某一状态的概率等于所有容器各自平稳时处于对应状态概率的乘积。

证明 因为πP=π解得的π是唯一的，所以只需要证明π'P=π'，即证也即:

定理1 说明，在实际计算中，只需要预先算出每台容器的平稳状态分布，再进行简单乘法运算就能得到n台容器的平稳状态分布。

2.4 动态负载容器的部署与资源预留问题

集群有m台宿主机，第l台宿主机Hl的可用资源可以用其容量Cl来描述，即Hl=Cl，1 ≤l≤m。容器的部署过程实际上是从容器到宿主机的一个映射过程，用矩阵X=来表示，当V(k)放置在Hl上时有Xkl=1，否则Xkl=0。

令W(k，t)表示容器V(k)在t时刻的资源需求量。理想情况下，所有宿主机在t时刻都能提供充足的计算资源。该约束条件可以表示为:

特别地，在初始时刻，即t=0 时，该约束满足。如果在t时刻该约束被破坏，则定义为发生了一次冲突。用vio(l，t)表示Hl是否在t时刻冲突，即:

冲突率为长时间运行过程中发生冲突的时间占总时间的比率，宿主机Hl的冲突率为:

CVR越小意味着容器动态迁移的几率越小。本文的策略目标是保证所有宿主机的冲突率保持在一个较低的值ρ以下，即使得:

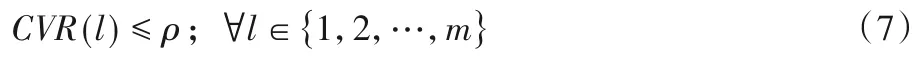
上述约束为宿主机的性能约束。下面给出面向动态负载的容器部署问题的定义。

定义1面向动态负载的容器部署问题是指，给出所有容器和宿主机参数V和H，找到一个从容器到宿主机的映射，使得在初始时刻满足容量约束以及在任意时刻满足性能约束的同时，总共使用的宿主机数量最少，也即:

满足容量约束（式（4）），当t=0 时；满足性能约束（式（7）），对所有t。

定理2面向动态负载的容器部署是NP（Non Polinomial）完全的。

证明 通过将NP 完全的装箱问题判定版本归约到所提出的面向动态负载的容器部署问题的判定版本来完成定理证明。装箱问题判定版本为:给定n个物品，第k个物品的大小是gk∈(0，1]，能否用m个单位容积箱子装下物品？

对任意一个给定的装箱问题判定版本实例，构造一个面向动态负载的容器部署问题（判定版）实例:令Nk为任意正整数，∀k∈{1，2，…，n}；令Ri(k)=gk，∀k，∀i∈{1，2，…，Nk}；再令Cl=1，∀l∈{1，2，…，m}；令ρ=0。这样可在多项式时间内完成归约，因此所提问题是NP完全的。 证毕。

3 面向动态负载的容器部署与资源预留

3.1 容器的资源预留策略

在单台宿主机上部署n台容器，这n台容器一共有N个状态，用Ri表示标号为i的状态的资源需求。不失一般性，不妨设R1≤R2≤…≤RN，则可以导出这n台容器最小所需容量Rq，其中q为满足如下关系的整数:

此时的性能约束满足:

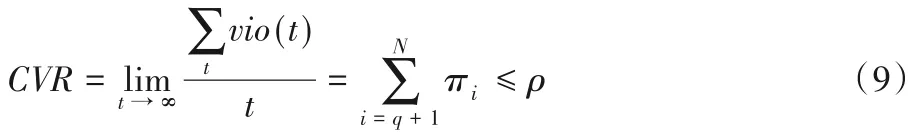
根据式（8），判断n台容器能否同时放置在某台宿主机l上的算法De(V，Hl)，具体描述见算法1 所示，其输出为能否放置的结果。

算法1 宿主机能否容纳容器（Determination）。

输入 特定宿主机l，容器的马尔可夫模型V={V(1)，V(2)，…，V(n)}；

输出n台容器能否放于特定宿主机l。

如果PI＞ρ，输出0（否）；否则输出1（是）。

3.2 面向动态负载的容器部署策略

现在考虑多台宿主机的情况。将n台容器部署到m台宿主机上，基于FFD 启发式算法设计部署策略，将n台容器按资源需求量的期望R(k)·μ(k)降序排序，并将m台容器按其容量降序排序。对给定的一个容器，依次尝试每个宿主机，若当前宿主机满足约束条件，则将容器部署在该宿主机上，否则尝试下一个宿主机直到这台容器被部署成功。算法MultiCons（n，m，d，V，H）的具体描述见算法2 所示，其中向量H包含所有可用的宿主机，d为单个宿主机上所能允许部署的最大容器数量。

记Nmax为n台容器各自的状态数的最大值，即Nmax=maxNk(1 ≤k≤n)。容器排序时间复杂度为O(nlbn)，宿主机排序复杂度为O(mlbm)，部署一台容器的复杂度为部署n台的复杂度为而容器部署算法总的复杂度由部署时间所决定，即Nmax一般是比较小的常数，d是确定的整数，故只是一个系数，算法的复杂度为O(nm)。然而，当实际运行中nm的规模不够大时是一个相当大的系数，直接导致部署时间延长。为了缩短部署时间，在3.3 节将提出一种估算最小资源预留量的预判方法。

算法2 面向动态负载的容器部署（MultiCons）。

输入 容器总数n，宿主机总数m；单宿主机允许部署最大容器数d；容器的马尔可夫模型V={V(1)，V(2)，…，V(n)}；宿主机模型H={H1，H2，…，Hm}。

输出 容器到宿主机的映射X=

3.3 面向动态负载的容器部署加速

在算法2 中，如果前面l台宿主机上已经部署了比较多（不妨假设为d-1台）容器，其将不再容纳任何有较大资源需求的其他容器。但算法2 在部署一台明显无法放置在这l台宿主机上的容器时，仍需要从第一台宿主机开始尝试，直到付出了的代价，才判断出前l台宿主机都无法容纳。显然，这种情况是对计算的极大浪费。本文考虑寻找一个可以简单计算出的参数，来判断容器是否有很大概率无法部署在特定宿主机上。本文先考虑所有容器的资源需求为独立的二项分布，如表1所示。

表1 容器的资源分布Tab.1 Resource distribution of dockers

正态分布的累积概率为Fz(zα)=P(Z≤zα)=1-α。现有一台宿主机上已部署k台容器，需要判断第k+1 台容器能否部署在该宿主机上。用X表示这k+1 台容器的总资源需求量，即X=X1+X2+…+Xk+1，根据中心极限定理，有:

本文分别用Xmin、Xmax表示Xk的最小值和最大值，进而得到:

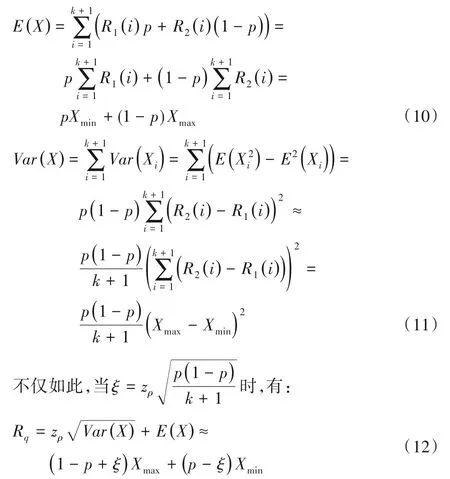
当Rq＞Hl时，可以判断第k+1 台容器无法放置在宿主机l上。这里Rq的计算有两个假定:1）所有的容器服从相似的概率分布。由于FFD将所有容器按照其资源需求量的期望排序，所以放置在同一台宿主机上的大多数容器具有相似的期望。在实际情况下，可以将容器按分布聚簇，再排序部署，使其更加准确。2）所有容器都是二状态的。在实际情况中，容器状态数会大于2，Xmax会导致实际结果偏大，在Xmax前加上修正α，得:

对于修正系数α，可以利用容器的分布估算。先考虑只有一台的情况:对于二状态的容器，易知α=1。对于N状态的容器(N≥3)有:

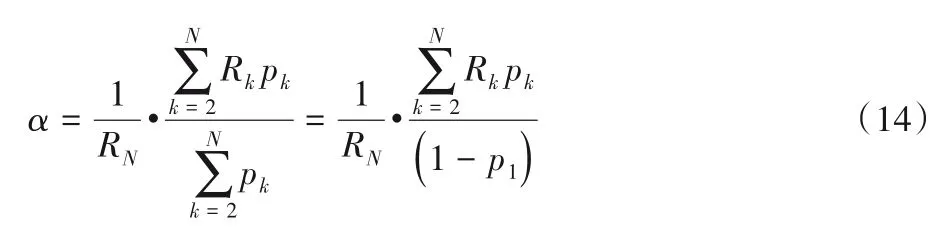
当有n台容器具有不一样的状态数时，有:

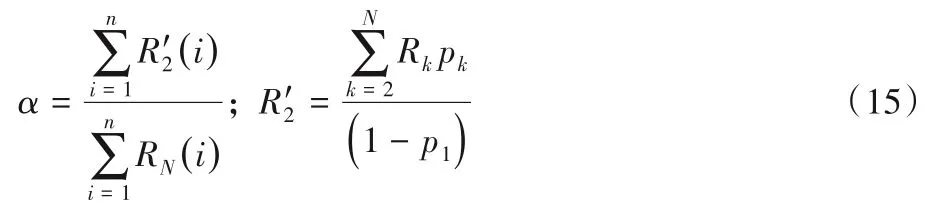
以式（14）、（15）计算出的α作为参考值，若在当前α下算法运行结果准确率比较低时，可以通过减小α来提高准确率；当运行时间较长且准确率较高时，可以通过增大α来缩短运行时间。据此，提出面向动态负载的容器加速部署策略（如算法3 所示），该算法能够结合宿主机和容器各自不同的状态进行动态部署。

这里提出用中心极限定理估算Rq方法的合理性在于:一般来说，若n≥9×max中心极限定理就可以得到较好的拟合效果。在实际的部署中，当容器的数量比较小时，资源需求量和计算出的Rq都远小于H，所以估算效果的好坏不影响结果；但当容器的数量比较大时，这种方法的估算效果好，得到比较准确的结果。

算法3 容器的加速部署（QuickMultiCons）。

输入 容器总数n；宿主机总数m；单宿主机允许部署最大容器数d；容器的马尔可夫模型V={V(1)，V(2)，…，V(n)}；宿主机模型H={H1，H2，…，Hm}。

4 实验与结果分析

4.1 实验概述

为验证部署策略的有效性，在基于国产软硬件环境的基础上，结合开源系统，设计了一系列实验，验证不同参数配置下所提设计算法的效果。

4.1.1 测试床环境

基于国产软硬件环境及开源系统，本文部署并测试环境运行的可行性。主要实验环境配置及具体参数包括:测试床服务器为浪潮SN5160M4（IntelE5-2680V4 CPU*2、256 GB（8*32 GB RDIMMG）DDR4 内存、1.2 TB 热插拔SAS 硬盘2.5"*6）；系统为中标麒麟（kernel-2.6.32；KVM-0.12）；资源管理系统为OpenStack R版本；语言环境为Python 3.8。

4.1.2 对比算法

在测试床的基础上，通过模拟程序行为实现了所提容器部署策略MULTI（MULTIple），并与三种常用的容器部署策略进行了比较:1）按谷值配置容器的策略RV（Resource with Valley）；2）按峰值配置容器的策略RP（Resource with Peak）；3）按谷值峰值的平均配置容器的策略RVP（Resource with Valley and Peak）。三种部署策略也都使用了FFD策略。在部署完成后，按照真实容器的分布，产生1 000 组实时数据进行仿真，出现冲突时测试床将容器动态迁移到其余空闲宿主机，记录运行性能结果。

4.1.3 验证指标

衡量部署策略的性能的参数包括部署一定台数容器所需的宿主机数（Physical Machines，PM）、冲突率（Capacity Violation Rate，CVR）和动态迁移次数（MIGration，MIG），其中PM、CVR、MIG分别是1 000组数据产生宿主机数目的最大值、冲突率平均值、动态迁移次数最大值。

4.1.4 实验参数

实验涉及的参数包括:容器数量（VM）、容器资源需求相对大小（R1∶R2∶…）、容器资源需求的平稳分布概率（P1∶P2∶…）、容器资源需求量的绝对大小（Rmean=宿主机容量（H）、宿主机允许的最大容器数（d）以及宿主机的性能约束（ρ）。

实验主要验证容器资源需求的分布区间（R1∶R2∶…）、绝对大小Rmean和平稳分布（P1∶P2∶…）在不同配置下对部署效果的影响，得到部署策略最优的参数配置范围。实验中容器有50%概率为二状态，50%概率为三状态。宿主机的容量H为（80，100）的均匀分布，d设为16，ρ设为0.04。三状态容器和二状态容器的资源需求量平稳分布分别如表2和表3所示，容器资源需求量分布如表4 所示。表2 的含义是对每一台容器，其P1在0～P内等概率随机取值，P2在0～(1-P1)内等概率随机取值，P3取1-P1-P2。表3和表4的含义类似。

表2 三状态容器的资源需求量平稳分布Tab.2 Resource demand stationary distribution of dockers with three states

表3 二状态容器的资源需求量平稳分布Tab.3 Resource demand stationary distribution of dockers with two states

表4 容器资源需求量分布Tab.4 Distribution of docker resource demand

累计进行了4组综合实验:

1）调节容器资源需求量的绝对大小:固定P=1，R分别取3～7，从而改变Rmean。

2）调节容器资源需求的平稳分布概率:分别在P等于0.2、0.4、0.6、0.8、1.0的情况下进行实验，并通过改变R固定Rmean=6.125。

3）调节容器资源需求的分布区间:固定P=1 和Rmean=6.125，改变R值调节容器资源需求。

4）部署策略运行的时间代价:取P=1和R=5，将10 000台容器分成100批，每批100台，按批次进行部署，并记录下每批容器部署的时间。

4.2 模拟实验结果

实验1 的结果如表5～6、图4 所示。RV 使用最少的宿主机，动态迁移次数最多。RP 动态迁移为零，使用的宿主机最多。RVP使用较少的宿主机，但动态迁移次数较多，冲突率会随容器条件的变化而产生较大起伏。MULTI 使用少于RP 的宿主机数，并且保持较少的迁移次数和较小冲突率。RV 与RVP 在R＜5 时的冲突率很小，R≥5 时更能体现MULTI 算法的性能效果。在现实中，一般宿主机上都会布置10 台以上容器［24］，所以模拟实验的结果在R=5 时更贴近真实的情况。随着R增大，MULTI 的PM增长速度大于RVP 的PM增长速度，这是因为R增大会导致单台宿主机上放置容器数量减少，即式（10）的k减小，得到更大的Rq。

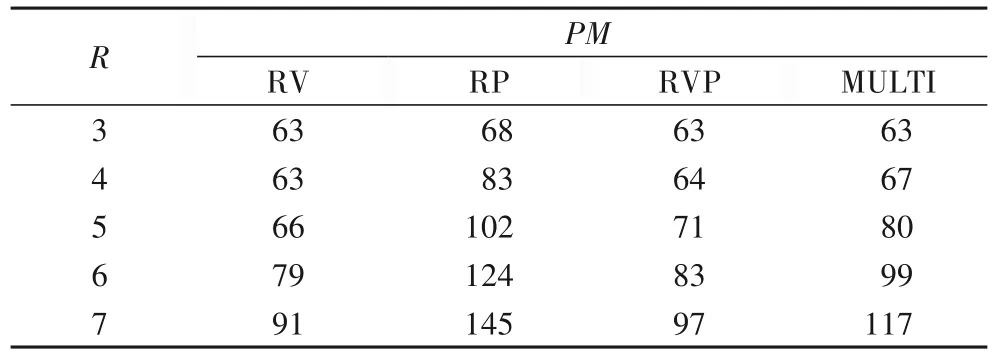
表5 PM与R的关系Tab.5 Relationship between PM and R

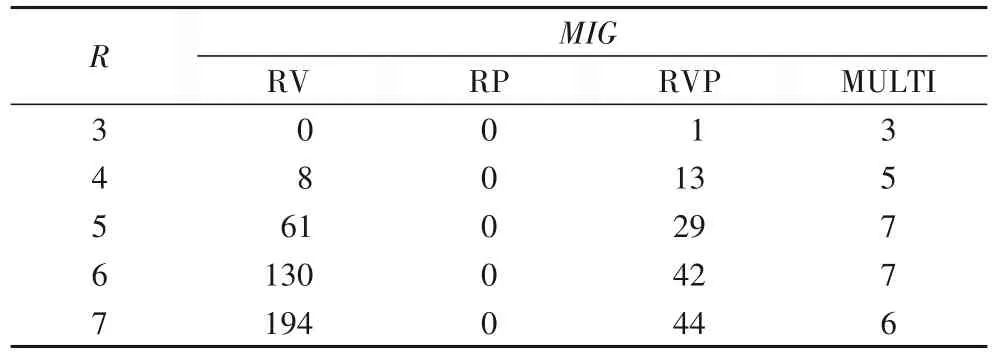
表6 MIG与R的关系Tab.6 Relationship between MIG and R

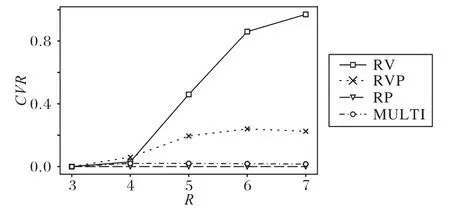
图4 CVR与R的关系Fig.4 Relationship between CVR and R

实验2的结果如表7～8、图5所示。随着P的增大，MULTI策略下的PM略有增大，但幅度比较小。增大的原因是:根据式（10）、（12），资源预留量Rq与容器资源需求的期望和方差有关，当保持Rmean恒定时，Rq的大小由容器资源需求的方差大小决定，经过简单计算可知基于表4的分布，P越大，容器资源需求的方差也越大，所需要的资源预留量越大，进而所使用的宿主机数量越多。RV、RP、RVP 三种算法的PM增大是因为R的增大。RV、RVP 的MIG和CVR都相当地大且不稳定，MULTI 的MIG一直保持在较小数值7，CVR也均保持在0.04以下，意味着当容器需要资源扩张的时候，其与宿主机的冲突率一直保持较低水平，也能够体现在宿主机上提前预留资源的好处。

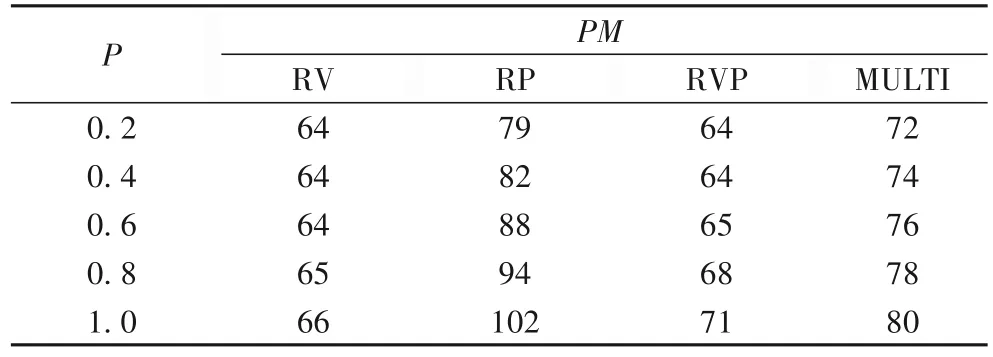
表7 PM与P的关系Tab.7 Relationship between PM and P

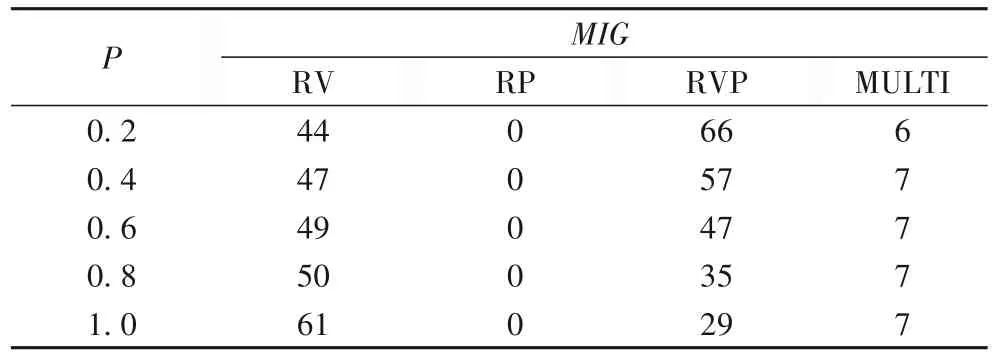
表8 MIG与P的关系Tab.8 Relationship between MIG and P

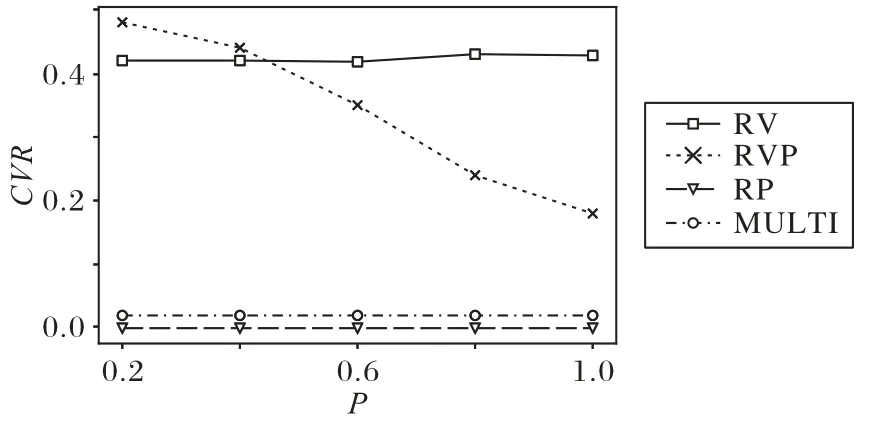
图5 CVR与P的关系Fig.5 Relationship between CVR and P

实验3 的R分别取3、5、7 时，资源需求量的分布如表9 所示。实验结果如表10～11，四种算法的MIG和CVR都比较稳定，RVP的MIG与MULTI的MIG保持着4倍左右的差距。

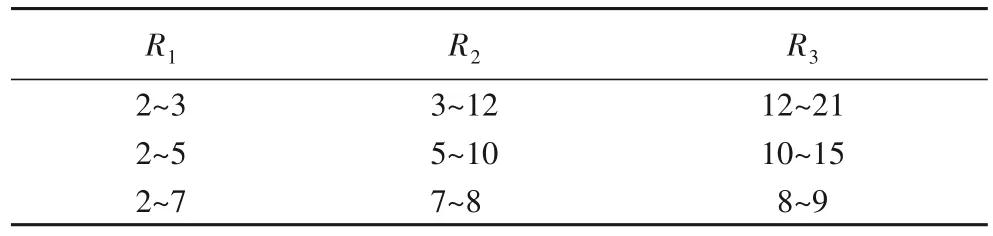
表9 P不变时资源需求量的分布Tab.9 Distribution of Resource Demand with fixed P

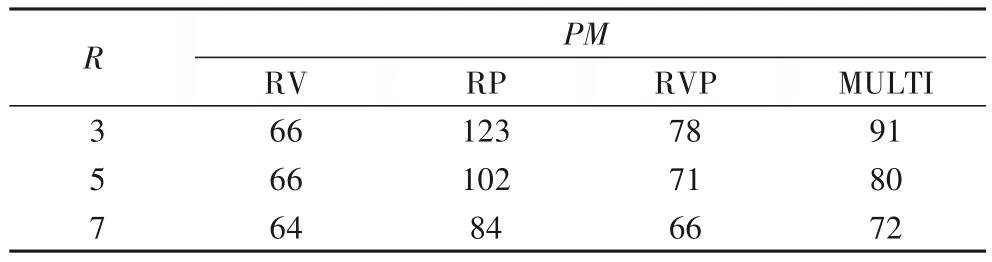
表10 PM与R的关系Tab.10 Relationship between PM and R

实验4的结果如图6所示，部署时间与当前已放置的容器数量呈线性关系，当已部署的容器数量过大时，部署时间也会变得非常长，表明容器迁移开销也相应变大。

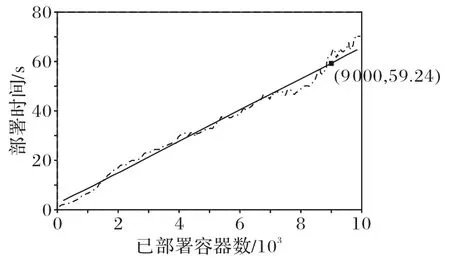
图6 部署时延与部署容器数量的关系Fig.6 Relationship between deployment delay and number of deployed dockers

综上所述，实验1 体现了容器资源需求分布的期望对部署结果的影响，实验2、3 用两种方式调节了容器资源需求分布的方差并研究了它对部署结果的影响，进而一方面也验证了式（10）、（11）、（12）结论的可靠性。面向多状态负载的容器部署策略的最大优点在于能够保持动态迁移次数和冲突率均稳定在一个较小的范围。

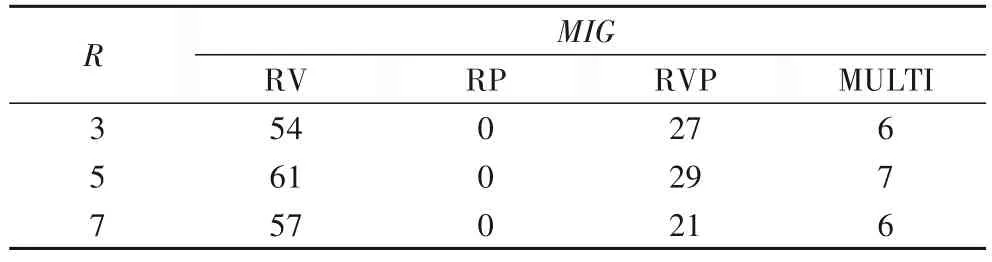
表11 MIG与R的关系Tab.11 Relationship between MIG and R

5 结语

容器技术在集群中发挥着重要作用，为用户提供按需式的资源服务。然而，传统被动的容器整合或是迁移无法应对动态的容器负载，给集群容器部署带来挑战。本文针对长效时间上容器整合与迁移的整体优化，提出了利用多状态马尔可夫链模型描述容器资源状态，并在宿主机资源预留的基础上提出了部署策略，还进一步优化部署的时延。实验结果表明，本文提出的策略能够在宿主机使用数量和动态容器迁移次数间达到较好的平衡。本文主要针对静态场景下的动态部署问题进行了探讨，但所提出的方法难以适用于在线场景，且资源需求类型的描述一定程度上影响了资源的分配策略，而资源需求的类型数量难以确定，这两方面将是下一步研究的重点方向。