基于VMD对SAR海洋内波参数的自动反演

张洪生，郑应刚，王有强

(上海海事大学 海洋科学与工程学院，上海 201306)

海洋内波是在海水密度稳定分层的海洋中产生的、最大振幅发生在海洋深处的波动现象。它通常是由海洋内部扰动源而引起的[1]，对海洋的质量、动量和能量的传输有重要作用[2]。对包括内孤立波在内的内波进行研究越来越引起人们的关注。直接观测是研究内孤立波的最佳手段[3]，可采用现场测量海水参数(温盐密、海水流速等)的方法对内波进行直接精确测量。但是由于直接观测法造价昂贵，仪器容易损害和丢失等，除了对一些重要的海域需要进行观测之外，开展大范围长时间的观测是不现实的。

目前，利用合成孔径雷达(synthetic aperture radar，简称SAR)图像进行内波研究是一个亟待发展的方向[4]。内波在传播过程中引起了海洋表面的辐聚辐散，使得海洋表面的粗糙度发生改变，因此内波在SAR图像上表现为明暗相间的条带[5]。SAR具有全天时、全天候、距离远、范围大、分辨率高等优点，已成为观测内波不可或缺的手段[6]。利用SAR图像研究内波一方面可以从SAR图像中反演内波的波长、波包间距等参数，另一方面可以利用实测资料进而反演内波的振幅和混合层深度等参数[7]。

基于SAR图像进行内波参数反演的方法主要有傅里叶变换法、小波变换法和经验模态分解(empirical mode decomposition，简称EMD)法等。傅里叶变换容易获取内波的主波信息[8]，而小波变换能够获取内波波形信息，但难在根据具体问题选择出最合适的小波基函数[5]。EMD方法是由Huang等[9]在1998年提出的，主要应用于物理学、生物学和海洋遥感等领域。EMD将信号序列分解成许多个本征模态函数(intrinsic mode function，简称IMF)分量，这些分量具有不同的特征尺度，与分解前的原始信号数据序列相比更有规律，但其存在模态混叠问题，影响到后续IMF的分离[10]，最终影响到内波参数的反演效果。

杨劲松等[10]分别利用傅里叶变换和小波变换提取出了SAR图像中的内波波长和波向等参数。甘锡林等[11]通过比较小波变换、傅里叶变换和EMD三种方法所提取的内波波长参数，验证了EMD方法的有效性。陈捷等[12]通过圆拟合算法估计SAR图像中内波传播方向，进而选取内波断面并利用 EMD 反演内波波长和振幅。Wu等[13]通过添加一种噪声辅助数据分析方法，提出了集合经验模态分解(ensemble empirical mode decomposition，简称EEMD)法，有效地克服了EMD模态混叠的问题。汪雄良等[5]运用EEMD方法所反演的前导波振幅与实测资料非常接近，结果表明EEMD方法较好地克服了EMD所存在的模态混叠问题。Yeh等[14]针对EEMD加入的白噪声不能完全中和的问题，提出了一种新的噪声增强数据分析方法——互补集合经验模态分解(complementary ensemble empirical mode decomposition，简称CEEMD)法，有效地消除了IMF中的残留噪声。该方法广泛地应用于信号的去噪[15]和故障特征的提取[16]等。

变分模态分解(variational mode decomposition，简称VMD)是基于严谨的数学理论而提出的一种新的信号分解方法，具有良好的鲁棒性和信号分解精度[17]，目前广泛应用于故障诊断等方面[18]。VMD分解后的固有模态函数的个数K需预先设置，通过不断地调整参数K就能解决模态混叠的问题。

目前，在对SAR影像中的海洋内波参数进行反演研究时，大多是人为选取内波断面数据或者通过辅助点进行拟合选取进而分析断面数据。文中通过获取SAR图像在Canny预处理后的条纹信息，再根据内波传播方向自动选取灰度剖面，然后利用EEMD信号特征自适应分解模态函数的特点，再将分解得到的有效模态数作为VMD中参数K的参考值，最后利用VMD分解后的数据进行内波参数反演。该方法解决了人为选取剖面可能导致的误差。通过对比分析EMD方法、EMMD方法和VMD方法的试验结果，并将VMD方法和EMMD方法反演的结果与实测数据资料进行比较，论证了VMD方法的可行性。

1 方法原理

1.1 基于KdV方程内波参数的反演原理

在内波参数反演中，最常用的是内孤立波理论。内孤立波理论是以KdV方程为基础的浅水波理论。一维非线性内孤立波方程为：

(1)

式中：η为内波波面位移，t为时间，c0为线性速度，α为非线性参数，β为频散参数。

假定海洋由两层密度不同的海水组成，即可概化为两层模型[19]。假设上层流体的深度为h1、密度为ρ1，下层流体的深度为h2、密度为ρ2，总水深H为：

H=h1+h2

(2)

求解式(1)可求得稳态的内孤立波解：

(3)

式中：η0为内孤立波的最大振幅，C为内波相速度，l为内孤立波半振幅宽度。C，c0和l的表达式分别为：

(4)

(5)

(6)

在海洋内波SAR图像中，由于内波的存在改变了海面的粗糙度，由此引起SAR图像灰度值的相对变化[20]。这种相对变化可以定义为：

(7)

(8)

式中：I0为海面的背景强度值，ΔI为含有内波区域的强度值与海面的背景强度值之差。x′=x-Ct为与内波一起运动的坐标，μ为松弛率，γ为Bragg波群速度与相速度之比，φ为内波传播方向(x方向)与雷达视向的夹角，B是与内波相速度、振幅、松弛率、内波深度和雷达视向等相关的系数。

由式(7)计算内波明暗条纹关系：

(9)

可得式(9)的解为：

x′=±0.66l

(10)

单个内波最亮点和最暗点之间的距离D可表示为：

D=1.32l

(11)

由式(6)可知：

(12)

由式(11)可知要反演出半振幅宽度l需要首先知道最亮点和最暗点之间距离D，由式(12)可知要反演出内波振幅除了需要已知半振幅宽度l外，还需要知道上下层流体深度h1和h2。

1.2 变分模态分解的原理

VMD实际上是对构造的变分模型进行寻优的一种算法，对所分解模态函数的中心频率和带宽采用交替方向乘子法(altarmate direction method of multipliers，简称ADMM)更新。首先保持中心频率不变更新带宽，然后再保持带宽不变更新中心频率，最后设置迭代结束的阈值。当达到预定的阈值则迭代结束并得到分解的信号，根据实际信号的特征频带自适应分解成多个IMF分量[17]。

VMD使用了EMD中IMF的定义，根据调制准则重新将IMF定义为调幅调频(amplitude modulated frequency modulated，简称AM-FM)的信号：

uk(t)=Ak(t)cosφk(t)

(13)

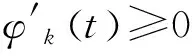
1) 首先对模态函数uk(t)进行希尔伯特变换(Hilbert transform)以求得解析信号：

(14)

2)得到的解析信号乘以e-jωkt，以使各模态函数移动到中心频率ωk：

(15)

3) 利用H1高斯平滑求解各模态函数的带宽之和，即L2范数梯度的平方：

(16)

4) 构造带约束的变分模型，在该约束下求各个模态函数的最优解：

(17)

(18)

5) 为了求解上述约束问题的解，引入二次惩罚项和拉格朗日(Lagrange)乘子将约束性问题转化为非约束性问题并求解，构造如下形式的增广拉格朗日函数：

(19)

式中：α为惩罚因子，取默认值2 000，λ为拉格朗日乘子，L为增广拉格朗日算子，〈〉为内积。

使用交替方向乘子法处理式(19)，得到模型的最优解，从而将原信号分解成K个IMF信号。具体步骤如下：

2)n=n+1；

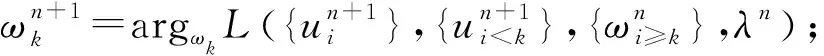
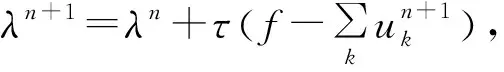
VMD按照信号特征进行分离，形成多个信号分量。其中，参数K的选取非常关键，并直接影响到参数反演的准确性。利用EEMD方法不需要事先设置分解模态个数且能够自适应分解的特点，将EEMD分解的层数作为VMD中参数K的取值。

2 图像预处理和数据分析

2.1 图像的预处理

研究所使用的SAR图像，为在巴士海峡附近于1995年6月16日02时29分发生海洋内波时的图像，选取的图像是欧空局ERS-1星载卫星所拍摄的SAR图像，图像像素大小为9 487×6 130，成像波段为C波段，极化方式为VV，像素之间的距离为12.5 m，经纬度范围为19°46′ N～23°03′ N，119°51′ E～121°01′ E。

ERS-1原始SAR图像如图1所示。在提取内波信号之前，需要对SAR图像进行预处理。由于下载的产品是单视一级产品，这是一个倾斜的范围图像，所包含复杂的数据尚未进行多视处理。首先需要对图像进行辐射定标(calibration radiometrically)，使像素坐标真实地反应雷达反射面的后向散射强度；其次将图像进行多视处理(multilook processing)，将图像从倾斜范围转化为地面范围后，图像具有较小的噪声和近似的平方像素间距；最后采用Gamma map[21]滤波对图像斑点噪声抑制，以减少对图像分辨率和信号分离的影响。采用欧空局(ESA)提供的SNAP软件对以上图像进行预处理，然后通过Canny处理得到筛选后的内波条纹信息[22]，最终得到的图像如图2所示。

图1 ERS-1原始SAR图像Fig. 1 ERS-1 original SAR image

图2 海洋内波SAR图像预处理结果Fig. 2 Image preprocessing results of oceanic internal wave with SAR

基于最小二乘法对图2中每一条内波条纹所构成的点集进行直线拟合K，得到每一条内波条纹的大致方向N，然后将N作为初始值，根据两点间距离最小性质进行迭代计算出每一条纹上每一点的真实方向N*，最后根据真实方向自动选取通过该点的灰度剖面，剖面示意见图3。此外，也可以利用该点所在的局部曲线段进行垂线求解得到该点剖面的大致方向。

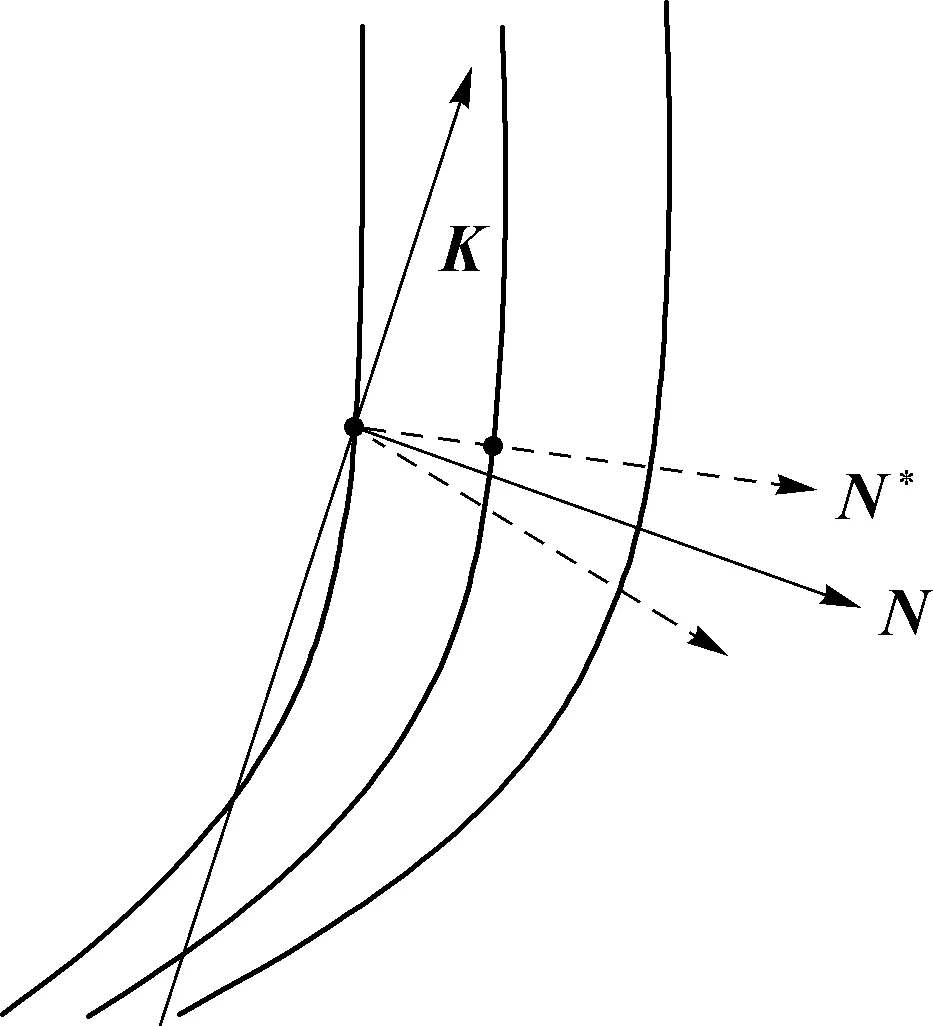
图3 迭代法选择剖面示意Fig. 3 Sketch of selection profile by iterative method

为了便于验证反演算法的有效性，选择了与文献[5]进行研究所采用的大致相同的区域。结合该地区已有的实测数据，对海洋内波振幅进行反演。因此仅对黑色线框区域进行研究，如图4所示。为了提取内波信号，选择了A点处的灰度剖面数据作为研究对象。

图4 灰度剖面数据位置Fig. 4 Location of gray profile data

2.2 数据处理结果与分析

以A点处的灰度剖面数据作为原始信号，分别做EMD、EEMD和VMD分解。其中EMD和EEMD均自适应分解为8层模态分量。分解结果如图5和6所示。

图5 内波剖面数据的经验模态(EMD)分解Fig. 5 Empirical mode decomposition of internal wave profile data

图6 内波剖面数据的集合经验模态(EEMD)分解Fig. 6 Ensemble empirical mode decomposition of internal wave profile data

杨洪柏等[23]针对EMD不需预先设定模态数自适应的分解特点，通过对EMD分解结果的分析，对VMD分解模态数K进行估计。针对EEMD同样具有自适应分解为一定数量模态数的特点，对分解的模态函数进行快速傅里叶变换(fast fourier transformation，简称FFT)频谱分析，结果如图7所示，进而近似求得VMD的分解模态数K。由图7可见，模态1频谱频带很宽，可视为噪声，无频率中心。模态4和模态5的中心频率两者都在1.672 Hz左右，可认为这两个分量具有一个频率中心，即可视为一个模态数。模态2、3、6、7和8可以分别作为一个独立的模态。因此VMD的分解模态数K可取6。VMD分解的结果如图8所示。

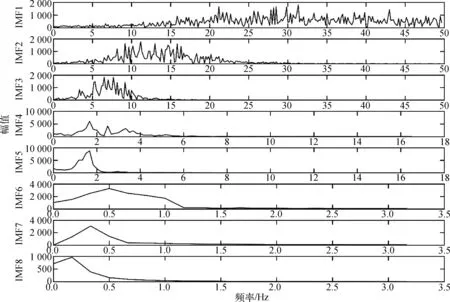
图7 集合经验模态分解各模态分量的频谱Fig. 7 Ensemble empirical mode decomposition of the spectrum of each modal component

图8 内波剖面数据的变分模态(VMD)分解Fig. 8 Variational mode decomposition of internal wave profile data

对原始信号进行分解的结果必有一层所含的内波信息较丰富。可以利用计算分解得到的每层信号归一化方差，来表示其内波相对能量的大小。因为内波蕴含着巨大的能量，可以用数值最大的归一化方差分量代表内波信息[10]。归一化方差表达为：

(20)

式中：σi为各层模态分量的方差，n为分解的层数。

分别计算每一层的归一化方差，计算结果如表1所示。由表1可知利用EMD方法分解之后的模态函数IMF5(EMD_IMF5)最大归一化方差为0.710 0。利用EEMD方法分解之后的模态函数IMF5(EEMD_IMF5)最大归一化方差为0.596 9。利用VMD方法分解之后的模态函数U2(VMD_U2)最大归一化方差为0.938 1。归一化方差的最大值对应的模态函数所含的内波能量也最大，因此可代表内波信号。

表1 经验模态分解、集合经验模态分解和变分模态分解各模态分量的归一化方差

将原始信号、EMD_IMF5、EEMD_IMF5和VMD_U2绘制在一起，如图9所示。从图9可看出，EEMD_IMF5和VMD_U2能够真实反映出原始信号上下起伏的周期性特征，同时验证了归一化方差最大的分量可代表内波信息这一准则。从图9也能看出，EMD_IMF5在区间[300，430]出现了模态混叠的现象，其中区间[350，400]中的内波信号出现在EMD分解的第四个模态函数IMF4中，模态混叠问题的出现影响到了下一步的分解。这就不能真实地反映出原始信号的特征。然而EEMD_IMF5和VMD_U2信号特征相近、其周期性强、上下起伏稳定，能够反映出真实的内波物理特性，因此这两者适合做内波参数的反演。

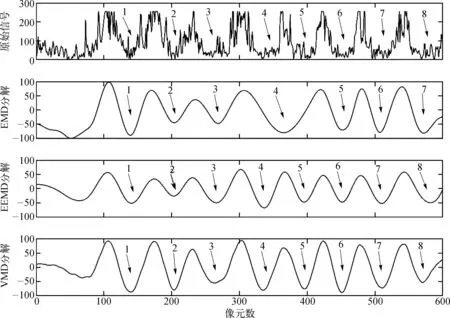
图9 原始信号、EMD_IMF5、EEMD_IMF5和VMD_U2Fig. 9 Original signal， EMD_IMF5， EEMD_IMF5 and VMD_U2

选取EEMD_IMF5和VMD_U2的数据。从左端开始算起，得到最亮点和最暗点之间的横坐标，进而计算最亮点和最暗点之间的像素距离差；然后根据相邻像素之间的距离为12.5 m，求得最亮点和最暗点的实际间距D；再根据式(11)可计算得到内波的半振幅宽度l。计算结果如表2和3所示。

表2 EEMD_IMF5中各孤立子波亮暗条纹之间的距离Di和半振幅宽度liTab. 2 The distance between the light-dark strip and the half-amplitude width of each solitary wave in EEMD_IMF5

表3 VMD_U2中各孤立子波亮暗条纹之间的距离Di和半振幅宽度liTab. 3 The distance between the light-dark strip and the half-amplitude width of each solitary wave in VMD_5

借助研究区域的实测数据，所研究的遥感图像区域位置混合层深度大约为46 m，总水深大约为4 000 m，前导波振幅大约为100 m左右[5， 11]。分别利用表2和3中的序号1半振幅宽度l，根据式(12)反演出该地区前导波的振幅分别为：

(21)

(22)

由式(21)和(22)可知，运用EEMD方法反演的结果与文献[5]中EEMD反演的结果97 m相差无几，这不仅说明了选取的剖面数据的可靠性和利用EEMD方法反演结果的有效性，同时也说明了VMD方法反演出的前导波振幅与实测资料十分吻合，且相比于EEMD方法更加接近实测数据，进而验证了VMD反演内波参数的可行性。

3 结 语

针对EMD方法在反演内波参数方面存在模态混叠的问题，提出了一种基于VMD对SAR遥感图像中的内波参数进行自动反演的方法。该方法先对SAR图像进行Canny处理，获取图像中的内波条纹信息，再根据内波传播方向自动选取灰度剖面；然后利用EEMD信号特征自适应分解模态函数的特点，将分解得到的有效模态数作为VMD中参数K的参考值；最后利用VMD分解后的数据进行内波参数反演。结果表明VMD方法不仅能够有效地克服EMD方法模态混叠的问题，提取的波形符合内波物理特性，而且反演的前导波振幅与实测资料相比基本吻合，这进一步说明该反演方法是有效的。目前仅使用一种方法对K值进行估计，运用多种方法来估计K值，并对比在不同方法下参数的反演结果是下一步要继续探讨的内容。