基于边界面模型的砂土中板锚循环承载力数值分析

王 强，刘海笑，李 洲

(天津大学 建筑工程学院，天津 300072)

随着海洋资源开发走向深水化，浮式油气开发平台、浮式波浪发电站和海上风力发电站等各类浮式海洋工程构筑物大量兴建。这些结构除了承受正常生产活动所产生的工作荷载外，还会受到风、浪、流等引起的循环荷载，且与地震荷载不同，这种循环荷载大多具有长期、持续和低频的特征，因此对系泊系统的要求极为严苛。锚固结构作为系泊系统中提供抗拔承载力的重要组成部分，是限制浮体漂移的关键所在。板锚是一种重要的嵌入式海洋工程锚固结构形式，尽管其体积小、重量轻，但仍然能够提供很高的承载能力，且对系缆角度的要求不高，同时具有经济实用、施工简单等优点[1]，因此板锚在系泊系统中被广泛应用。

海洋土的非线性动力特性，决定了嵌入其中的结构在循环荷载作用下会产生复杂的荷载—位移响应，也对结构的承载力设计和维护带来诸多困难。现行设计规范如挪威船级社制定的DNV规范[2]和美国船级社制定的ABS规范[3]，在针对海洋结构基础的循环承载性能评估中，都建议通过绘制土体循环强度轮廓图(the cyclic contour diagram)的方法来考虑循环荷载效应。该方法需要考虑结构不同位置处土单元的受力状态，通过一组单调三轴压缩，拉伸和直接剪切试验，以及系列循环试验来获得完整的循环强度轮廓图，进而利用插值法获得各土单元的循环强度[4]。

目前针对嵌入式海洋结构循环承载性能的研究常局限于黏土[5-6]，由于砂土更为复杂的应力—应变响应，针对板锚循环动力特性的研究还处于初步阶段。Bemben等[7-8]对饱和松砂中的板锚进行了系列循环试验，试验中观察到了明显的“棘轮效应”。Petereit[9]针对循环荷载幅值对板锚循环承载特性的影响进行了系列模型试验，研究发现循环幅值越高，板锚位移累积速率越大。Chow等[1，10]针对板锚在密实砂土中的行为特性做了大量试验研究，考察了不同性质循环荷载作用下板锚的荷载响应特性。由于板锚在长期循环荷载作用下承载性能的变化，用试验模拟耗时耗力，并且随着深水化发展，现场试验的开展难度越来越大。因此数值分析模型成为研究循环荷载作用下板锚承载特性的重要选择。

现有海洋工程构筑物循环承载数值分析模型主要分为拟静力分析模型[11-12]、显式经验模型[13-14]以及动力本构数值分析模型[15-17]。其中，动力本构数值分析模型基于能够合理反映砂土动力响应特性的本构模型理论，是评估嵌入式海洋工程结构循环承载特性的重要手段，也受到了越来越多研究者的关注。现有动力本构数值模型具有模拟板锚循环动力响应的能力，但所采用的本构理论自身具有局限性。如基于广义应力、应变建立的宏元模型[1，18]无法反映土体结构自身的动力响应，也无法考虑结构特征改变对承载力的影响。以及基于具有高频、瞬时特点的地震荷载建立的本构模型[15-16]无法模拟在低频、长期循环荷载作用下结构在砂土中的动力特性。目前，可以合理反映此类循环承载响应特性的本构模型仍然处于理论研究阶段，没有成熟的数值模型可用于嵌入式海洋工程结构的分析模拟。因此，一种能揭示长期循环荷载作用下板锚—海床土相互作用机理，进而可用以评估板锚循环承载力的数值分析模型，亟待研究、建立。

鉴于以上原因，基于一种适用于饱和砂土循环动力分析的边界面模型[19]，通过修正模型塑性模量和硬化参数，使其能够更加准确地描述循环荷载作用下土体的塑性变形。利用带误差控制的显式积分算法，以张量形式，将上述边界面塑性模型编写成可供有限元软件调用的用户自定义材料子程序。建立土体单元数值模型以模拟砂土的排水静、动三轴试验，考察模型合理描述砂土在不同荷载条件下力学响应的能力。最后建立饱和砂土中板锚循环承载分析的数值模型，针对板锚在砂土中的单调抗拔特性和循环承载特性进行数值分析，并考察循环荷载要素对板锚循环承载特性的影响。

1 适用于饱和砂土动力分析的边界面塑性模型

董建勋等[19]和高源等[20]以相应于历史所受最大应力的最大加载面作为边界面，以此来记忆应力历史。初始加载时，应力点始终位于边界面上，边界面随着应力的增加而扩大；卸载时，应力点向内移动，最大应力保持不变，边界面固定；再加载时，在应力超过历史最大应力之前，边界面一直固定，应力状态达到最大应力状态时，应力路径与边界面相交，在后续加载中，边界面以初始加载的形式扩大，更新最大应力历史。

采用由Bardet[21]提出的修正椭圆边界面，边界面图形如图1所示，边界面方程如下：

图1 边界面塑性模型的应力更新流程Fig. 1 Stress update flow chart of boundary surface plasticity model

(1)

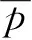
(2)

(3)

(4)

式中：J2、J3分别为偏应力第二、三不变量；c=Me/Mc，Me为三轴拉伸时的临界状态应力比，表达式为：

(5)

(6)

式中：i表示第i加载步；p0为初始围压；(opi，oSi)为第i步的映射中心坐标。

砂土的体积变化同时取决于所受荷载和材料属性，为了合理反映砂土受力后的体积变化特性，采用非相关联的流动法则，剪胀函数表达式如下：

(7)

式中：d0为模型常数；rij=sij/p为偏应力比张量；Md为剪胀应力比；nij为塑性偏应变方向。其中，

(8)

式中：m为模型参数。ψ为表征砂土属性的状态参数，表达式为：

ψ=e-ec

(9)

式中：e和ec分别为当前孔隙比和临界状态孔隙比，ec与当前平均有效应力p有关。ec采用Li等[23]提出的表达式：

(10)

式中：pat为标准大气压；eΓ、λ、ξ为土体固结压缩曲线的拟合参数，描述土体的临界状态。

nij表征塑性偏应变方向，表达式为：

(11)

针对砂土的循环承载，土体结构的变化对土体刚度有显著影响，该变化主要分为两类，一类是循环荷载作用下土体逐渐密实，土体结构更加稳定，另一种是负塑性体积应变造成的破坏[24]。为了准确反映这两种变化对土体刚度的影响，采用如下硬化公式：

(12)

式中：

(13)

(14)

式中：

(15)

式中：α、β、χ为控制土体结构变化速率的材料常数，L为加载指数。L表达式为：

(16)

弹性剪切模量G和弹性体积模量K采用如下表达式：

(17)

(18)

式中：G0为模型参数；υ为泊松比。

塑性模量表示式如下：

(19)

(20)

式中：n为模型参数。

应力—应变关系的增量方程可以表示为：

(21)

式中：

(22)

(23)

(24)

利用上述适用于饱和砂土动力分析的边界面塑性模型得到土体在特定加载路径下的应力—应变关系，并最终用于岩土工程边值问题求解，需要采用有效的数值积分算法对模型进行数值实现。采用带误差控制的改进Euler积分算法，通过自动调整各子增量步的大小来控制积分误差[25]。该方法是一种子增量步应力积分算法，通过监控局部截断误差来控制子增量步步长，将应变增量{Δε}离散成系列子增量步应变增量{Δεs}，即Δε=ΔT·Δεs。T为无量纲时间，初始时间T=0，ΔT为步长控制参数，值域为(0，1]，初始增量步中ΔT=1。通过监控局部截断误差来控制子增量步步长。截断误差通过每个子增量步应力增量的误差值来计算，如果截断误差超过指定容许值SSTOL，则使用更小的子增量步进行积分[20]。图1展示了积分算法的主要流程。

2 三轴试验数值模型验证

为了考察建立的本构模型描述砂土力学响应的能力，同时验证带误差控制的显式积分算法的有效性和准确性，首先将建立土体单元数值模型以模拟完全排水条件下的砂土静、动三轴试验。

2.1 静三轴试验模拟

Verdugo等[26]对Toyoura砂进行了系列三轴试验，试验所用Toyoura砂是一种均匀细砂，平均粒径0.17 mm，不均匀系数1.7，最大和最小孔隙比分别为0.977和0.597，相对体积质量2.65。针对3组具有不同密度砂土的排水三轴试验进行模拟，模型参数见表1，模型参数采用董建勋等[19，27]建议的方法进行确定。3组土样固结压力均为100 kPa，孔隙比分别为0.996、0917和0.831，试验加载采用应变控制加载，加载过程中保持侧向压力恒定不变。

表1 模型参数Tab. 1 Model parameters

图2中，ε1为轴应变，q为偏应力，e为孔隙比，由图2可以看出，剪切荷载作用下，3组不同孔隙比土样的应力—应变和应力—孔隙比计算结果与三轴试验结果相吻合，说明边界面塑性模型所采用的塑性模量和剪胀函数能有效反映在单调荷载作用下砂土的力学特性。

图2 单调荷载下Toyoura砂三轴压缩试验数据与模型对比Fig. 2 Comparison of Toyoura sand under monotonic loading between data from triaxial compression tests and results from modelling

2.2 动三轴试验模拟

Pradhan等[28]在循环荷载下针对砂土的应力—应变关系做了一系列排水三轴试验，试验所用砂为Toyoura砂。选取其中2组正常固结试验进行模拟分析，2组试验土样初始孔隙比分别为0.832和0.845，平均主应力P′为100 kPa，且在试验过程中保持恒定。

图3和图4分别对比了孔隙比为0.832的Toyoura砂在平均主应力和循环应力幅值都保持不变时的循环荷载作用下循环动力特性以及孔隙比为0.845的Toyoura砂在平均主应力恒定且循环应力幅值不断增大的循环荷载作用下循环动力特性。从对比模型计算结果与试验数据可以看出，边界面模型可以合理反映循环荷载作用下砂土的排水动力响应特性。

图3 循环荷载下Toyoura砂应力比—应变曲线的循环三轴试验数据与数值模拟对比Fig. 3 Comparison of stress-strain curve of Toyoura sand under cyclic loading between data from triaxial compression tests and results from modelling

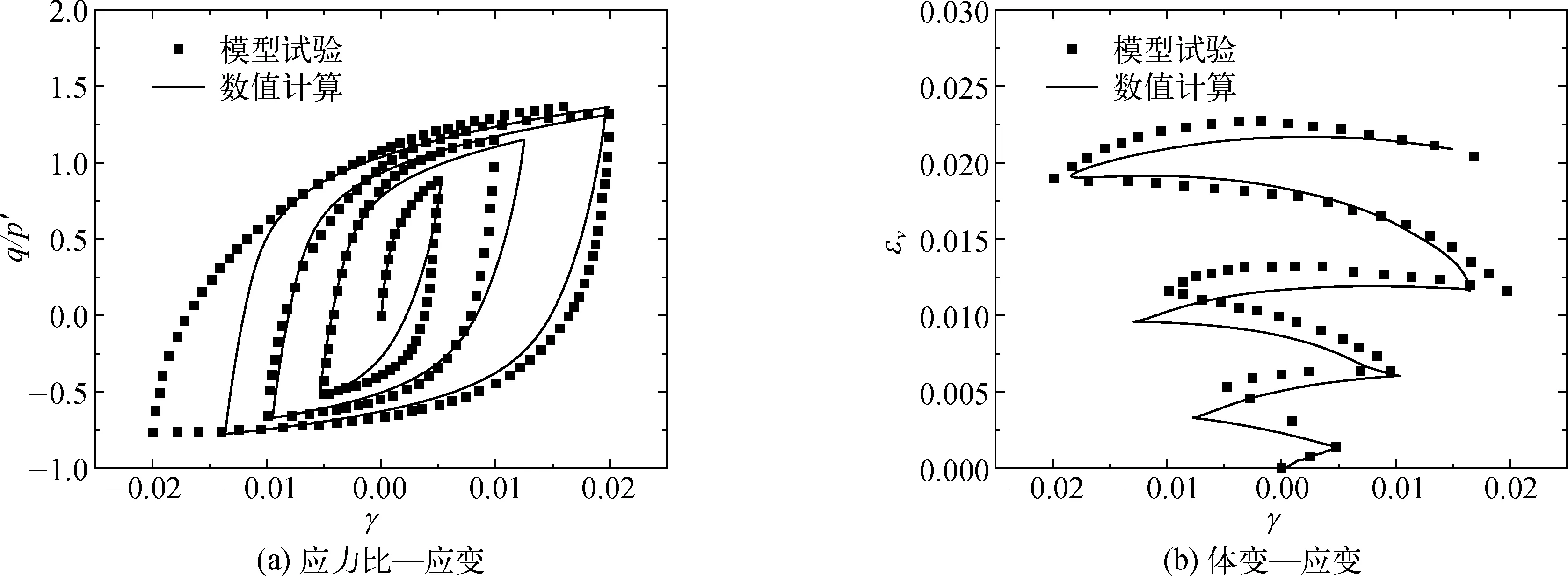
图4 循环荷载下Toyoura砂循环三轴试验数据与数值模拟对比Fig. 4 Comparison of Toyoura sand under cyclic loading between data from triaxial compression tests and results from modelling

3 板锚承载力分析

3.1 板锚极限承载力分析

Dickin等[29]针对板锚在砂土中的单调抗拔效应做了系列离心机试验，考察了不同板锚尺寸和埋深下板锚的荷载—位移响应。试验采用的是干燥、均匀的Erith石英砂，80%的粒径在0.125 mm到0.25 mm之间，不均匀系数为1.5，密砂和松砂的容重分别为16 kN/m3和14.5 kN/m3，离心机加速度为40g，试验所用板锚为25 mm宽、3 mm厚的不锈钢模型板锚，模型参数见表1。

由于锚和荷载都是对称的，可利用对称性直接建立四分之一的三维轴对称数值模型进行分析，垂直对称轴通过板锚的中心，选取适当的边界位置(3B)以消除边界效应，有限元模型如图5所示，其中B为板锚宽度，H为板锚埋深。为板锚施加刚体约束，将板锚的运动约束为参考点的运动，给土体底部施加固定约束，在对称面上施加对称边界条件，板锚和砂土之间采用绑定接触。土体单元以及板锚单元的单元类型为C3D8，网格尺寸对于模型的计算效率和精度有很大的影响，通常网格尺寸越小，单元个数越多，计算精度越高，但计算效率越低。为了提高模型的计算精度，同时又保证计算效率，需要对网格尺寸进行考察，以获得最优化的网格尺寸。研究考察了3组网格密度，最小网格尺寸分别为0.05B、0.025B、0.0125B，网格数分别为66 781(Mesh1)、247 491(Mesh2)、963 200(Mesh3)，如图6所示，W是板锚上拔位移，B为板锚宽度，F为四分之一板锚所受抗拔力。结果显示3组网格密度所计算的结果都已经收敛，但是网格尺寸越小，曲线越光滑，综合考虑计算精度和计算效率，研究选取最小网格尺寸为0.025B。

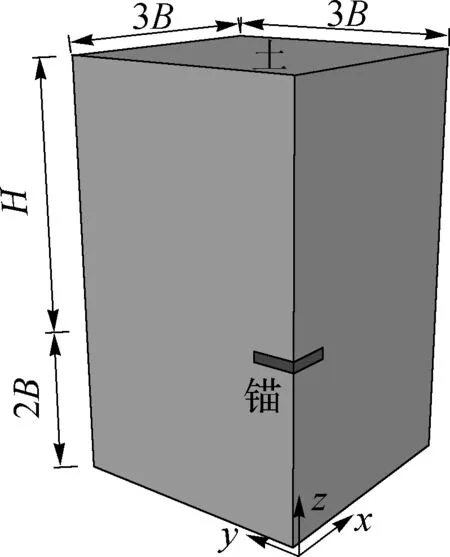
图5 数值模型示意 Fig. 5 Schematic diagram of numerical model

图6 网格考察结果Fig. 6 Results of grid survey

图7、图8展示了在不同埋深下，模型试验与数值模拟获得的不同长宽比板锚在松砂和密砂中的荷载—位移响应曲线。由图可知，随着板锚长宽比、埋深和土体密度的增大，最大拉拔承载力也随之增大，数值计算得到的最大抗拔承载力、对应最大抗拔承载力的位移、失效后残余抗拔承载力均与实测试验结果一致。

图7 板锚在砂土中的荷载—位移曲线(L/B=1)Fig. 7 Load-displacement curve of plate anchors in sand (L/B=1)

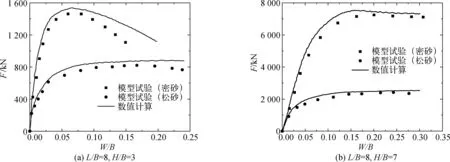
图8 板锚在砂土中的荷载—位移曲线(L/B=8)Fig. 8 Load-displacement curve of plate anchors in sand (L/B=8)

针对浅埋工况(H/B=3)，在密砂中，初始阶段承载力随着板锚位移的增加而迅速增大，增长速率随着接近最大值(峰值)而逐渐减小，出现明显峰值后，承载力逐渐减小。在松砂中，不同长宽比的板锚所受荷载以不同的速率单调增加到一个最大值，之后板锚继续上拔，但承载力几乎不再发生变化。针对深埋工况(H/B=7)，在密砂和松砂中的板锚荷载—位移曲线都未观察到明显的峰值。

图9展示了在不同埋深下板锚上方土体位移的差异，可以看出，浅埋时，土体位移会延伸到土体表面，而深埋时，只在锚上方的局部区域观察到位移变化。上述现象Ilamparuthi等[30]在圆形板锚的单调抗拔承载力试验研究中也有报道，通过对砂土中浅埋和深埋板锚的单调抗拔模型试验，总结出两类典型破坏模式：浅埋时，从板锚到砂土表面会形成一个向上隆起的土锥台，即整体剪切破坏；深埋时，板锚上方会形成一个气球状的破裂带，即局部剪切破坏，两种破坏模式如图10所示。随着埋入深度的增加，板锚的破坏行为由整体剪切破坏转变为局部剪切破坏。

图9 板锚在松砂中的位移云图Fig. 9 Displacement contours for a plate anchor in sand

图10 松砂中板锚的失效机理Fig. 10 Failure mechanism in sand above plate anchor

综上，建立的适用于饱和砂土中板锚排水循环动力分析的数值模型能够很好地模拟板锚在砂土中的行为特性，并有效反映板锚尺寸、埋深和土体密度对板锚极限抗拔承载力的影响。

3.2 板锚循环承载力分析

Petereit[9]对圆形板锚在砂土中的循环承载特性做了大量模型试验，试验所用砂为Ottawa砂，其相对体积质量为2.65，不均匀系数为1.9，摩擦角为40°，最大密度1.7 g/cm3，最小密度1.47 g/cm3，相对密度80%，孔隙比为0.61。板锚直径为10.16 cm，厚度为0.635 cm，板锚初始埋深为914 cm，试验中此埋深下板锚单调抗拔承载力Pu=4 895 N，试验用循环荷载为正弦荷载，如图11，周期T范围为0.5～10.0 s。模拟的试验组为：循环荷载周期T为4 s，循环幅值Qc=25%Pu、50%Pu和75%Pu，试验用砂密度1.65 g/cm3，试验工况为板锚水平埋置，施加竖向荷载向上拔出板锚，模型参数见表1。

图11 循环荷载参数Fig. 11 Parameters of cyclic load

3.2.1 板锚极限承载力分析

为了验证Ottawa砂模型参数的准确性，首先针对板锚在Ottawa砂中的单调抗拔过程进行模拟。图12给出了模型试验和数值模拟中板锚在单调荷载作用下的荷载—位移曲线，该工况埋深比H/B=9，符合3.1节中介绍的深埋条件，其荷载—位移响应也与深埋板锚上拔行为类似，因此再次证实了所建立的适用于饱和砂土中板锚排水循环动力分析数值模型的有效性。

图12 板锚在单调荷载作用下的荷载—位移曲线Fig. 12 Load-displacement curve of a plate anchor under monotonic load

3.2.2 板锚循环承载力分析

图13中，U表示板锚位移，F为板锚所受荷载。可以看出，初始加载时，板锚在荷载作用下会产生一定位移，随后卸载，板锚位移会恢复一部分，但是无法回到初始位置，即一次加—卸载之后土体产生了塑性变形。再加载时，板锚再次经历移动和回弹，由图13(a)可以看出，在后续加—卸载过程中，每一周次产生的塑性变形逐渐减小直到一个稳定值。Bemben等[8]和Hanna等[31]对长周期循环荷载下板锚在饱和砂土中的承载力做了模型试验，观察到了类似现象：当承受循环荷载时，板锚会产生不可恢复的位移，发生明显的“棘轮效应”，即在应力控制循环加载下产生循环塑性应变累积[32]。随着荷载周次的增加，每周次产生的位移会逐渐减小，累积位移速率虽然减小，但并没有停止。这种永久位移累计速率随着循环次数的增加而逐渐减小的特性，与荷载条件有关，但文中本构模型中的硬化公式C(ξ)利用应变累积来考虑应力历史的影响，得到的土体刚度随加载周次的变化速率偏小，所以针对大周次“棘轮效应”的模拟效果有限。

图13 板锚在循环荷载作用下的荷载—位移曲线(Qc=75%Pu)Fig. 13 Load-displacement curve of plate anchor under cyclic load (Qc=75%Pu)

3.2.3 循环幅值影响

图14给出了不同循环幅值的循环荷载作用下，板锚的位移—周次响应，图中N为循环周次，U为板锚位移。由图可以看出，循环幅值越大，初始位移和位移变化率越大，这是因为更高的荷载会给周围的土体带来更大的应变。从图中可以看出，每组试验中，数值计算的位移值一开始都先小于试验测量值，但随着循环周次的增加逐渐增大并超过测量值，且循环幅值越大，越早完成超越。这是由于数值计算中采用的几乎恒定的塑性变形率和实际变化的塑性应变率的差别所导致的，在初始阶段，数值计算的累积塑性变形略小于模型试验所测得的塑性变形，但随着模型试验中累积塑性变形速率的减小，数值计算的累积变形会逐渐超过模型试验所测得的结果。

图14 板锚在不同幅值循环荷载作用下位移—周次响应曲线(Qm=40%Pu)Fig. 14 Displacement-cycle number response curve of plate anchors under cyclic loads of different amplitudes (Qm=40%Pu)

3.2.4 荷载均值影响

图15给出了Qc相同、Qm不同的工况对应的位移—周次响应曲线，可以看出，荷载均值Qm越大，初始位移越大，但是位移变化率越小，上述结论与离心机试验结论[33]相同。因此，对于长期承受循环荷载的嵌入式海洋工程结构，可以通过增大循环均值Qm的方法来减小循环位移累积，延长服役寿命。

图15 板锚在不同荷载均值循环荷载作用下位移—周次响应曲线(Qc=10%Pu)Fig. 15 Displacement-cycle number response curve of plate anchors under cyclic loads with different mean values (Qc=10%Pu)

4 结 语

利用带误差控制的显式积分算法，将一种适用于饱和砂土排水循环动力分析的边界面塑性模型编写成可供有限元软件调用的用户自定义材料子程序，从而建立起适用于板锚在饱和砂土中循环承载分析的数值模型。得到以下结论：

1) 针对Toyoura砂的3组排水静三轴试验和2组排水动三轴试验进行了模拟，数值计算结果与模型试验结果相吻合，验证了模型具备合理描述砂土在不同荷载条件下的力学响应的能力；

2) 建立了饱和砂土中板锚承载分析的数值模型，并模拟了板锚单调上拔过程。数值计算得到的最大抗拔承载力、对应最大抗拔承载力的位移、残余抗拔承载力与离心机试验结果一致，表明建立的动力本构数值模型可以有效模拟板锚在砂土中的行为特性；

3) 利用以上建立的数值分析模型，模拟板锚在砂土中的循环承载过程。结果表明，随着循环荷载的施加，板锚永久位移逐渐累积，循环荷载会导致板锚产生累积位移。通过考察循环荷载要素对板锚循环承载特性的影响，得到了与试验结果相吻合的结论，即循环幅值越大，初始位移和位移变化率越大；循环均值越大，初始位移越大，但位移变化率越小。

4) 尽管利用建立的适用于板锚在饱和砂土中循环承载分析的数值模型能够获得上述结论，但仍然存在以下3个问题：① 迭代计算时间长；② 循环周次较大时计算累积误差大；③ 确定模型参数需要较多室内试验。动力本构模型是根据应变或应力增量进行计算，每一个循环周次需要大量的增量步，如果循环周次较大，计算时间就会很长，并且每一个增量步都会有一定的计算误差，随着循环周次的增加，累计误差也会越来越大。而且动力本构模型参数较多，用于循环承载计算需要大量的室内土动力试验来标定参数。这3方面原因制约了文中建立的适用于板锚在饱和砂土中循环承载分析的数值模型广泛应用于工程计算。