含有非匹配干扰和未知动态的非仿射系统滑模控制算法

朱 斌 ,孙瑞胜 ,陈洁卿 ,陈 伟 ,严大卫

(1.南京理工大学能源与动力工程学院,江苏南京 210094;2.中国运载火箭技术研究院战术武器事业部,北京 100076)

1 引言

近年来,通过与自适应、神经网络、模糊控制等理论的相互结合,滑模控制[1-4]、反步法[5-8]、反馈线性化[9-10]等方法在非线性控制领域涌现出许多新的成果.然而,现有的研究成果绝大多数是解决仿射形式的非线性系统控制问题,针对非仿射形式的非线性系统,相关的研究成果仍然较少[11].非仿射系统没有“控制增益”和“控制方向”的概念,这使得针对仿射形式的大量非线性控制方法难以直接使用.但对于真实物理系统而言,非仿射系统是比仿射非线性系统更为广泛的存在.因此,对非仿射系统控制方法的研究可以解决更多的实际控制问题.

目前,针对非仿射系统控制问题的主要思路有两种[12].一是通过隐函数定理或中值定理将系统转化为仿射形式,二是从原有模型中分离出线性控制项,然后利用神经网络/模糊控制等逼近结构获取新的非线性项.例如,文献[13]通过自适应网络对非线性项进行逼近.文献[11]则提出一种采用Nussbaum型函数处理非线性项的方法.但文献[13-14]指出,基于神经网络/模糊控制等逼近结构的方法在处理高级系统时,往往需要虚拟控制量的导数信号,增加了设计难度.并且神经网络等方法待设计参数多,输入复杂,运算量大.而文献[14]提出了一种使用扩张状态观测器(extended state observer,ESO)进行非线性项估计的方法.ESO结构简单,估计能力强,这种方法大大简化了估计结构的设计难度.然而需要注意到,ESO本质是一类高增益观测器,因此存在高增益观测器中的峰化现象[15],可能导致状态变量超出稳定吸引区导致系统发散.特别是某些场景中,需要ESO有很快的估计速度,而提高增益是增加观测器估计速度的一种最常见选择,但这也带来一些负面影响.例如提高增益后,观测器在收敛初期的估计误差就可能出现超调、振荡等现象.这些都可能导致状态变量超出稳定吸引区导致系统发散.对此,本文提出了一种基于预设性能函数的改进ESO结构,以实现对估计过程中瞬态性能表现改善的目的.改进结构通过引入预设性能函数(prescribed performance function,PPF),并进行估计误差变换,在不改变ESO原有能力的基础上,限制估计误差始终保持在一个预先设计的边界之内,达到了约束瞬态性能表现的目的.进而改善估计过程中出现的超调和振荡现象,使得ESO在拥有较快估计速度的同时,其估计初期的瞬态性能表现仍然能满足设计约束要求.

在通过ESO的变换后,非仿射系统可以表达为如下形式的二阶系统:

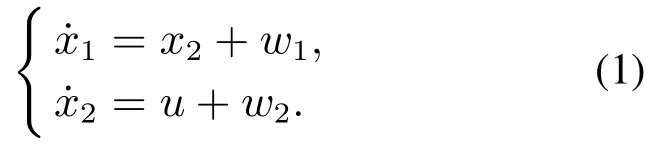
系统(1)是典型的包含匹配干扰和非匹配干扰的二阶系统.其中w1和w2是每阶方程中除去第1项之后的未知总和扰动.在使用传统自抗扰控制方法对式(1)进行控制时,有两种方案:一种是设计两个级联的自抗扰控制器,另一种是直接将u设计为一个能够克服上述两种类型干扰的鲁棒控制律.但无论哪种方法,都需要考虑w1和w2的估计误差所带来的影响.本文提出了一种基于滑模控制的方法,并对滑模面的设计做出改进,将所有不确定误差的处理统一转移到滑模面的设计当中,使得系统具有更高的鲁棒性.改进方法放宽了传统滑模面s=0的要求,只需要s收敛至一充分小的区间即可.同时,利用ESO的估计能力将未知非仿射系统变换为一个已知的仿射系统,克服了滑模控制(sliding mode control,SMC)需要模型已知或部分已知的条件,拓宽了SMC的应用范围.

2 问题描述

2.1 含有非匹配干扰的非仿射系统模型

考虑如下含有非匹配干扰的二阶单输入单输出(single input single output,SISO)非仿射系统:

其中:x1和x2是系统的状态变量,u是系统的控制输入,d1和d2是未知外部扰动,而f1和f2是含有未知动态的非线性函数.对于系统(2),给出如下假设.

假设1系统状态x1和x2是已知的.

假设2f1和f2是光滑连续非线性函数,且存在正数γ1和γ2,使得对于所有(x1,x2,u)∈R3,满足

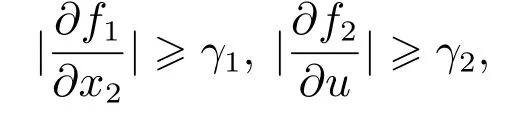
且偏导数符号已知.干扰d1(i=1,2)是可微的,且导函数有界.

假设2是系统(1)全局可控的充分条件[16].此外,偏导数的符号与具体对象相关联,本文为了便于后文公式的书写及讨论,假定偏导数符号均为正.在处理具体问题时,则需要根据系统特性确定符号正负.

令yi1=xi(i=1,2),并将系统(2)变形为如下形式:

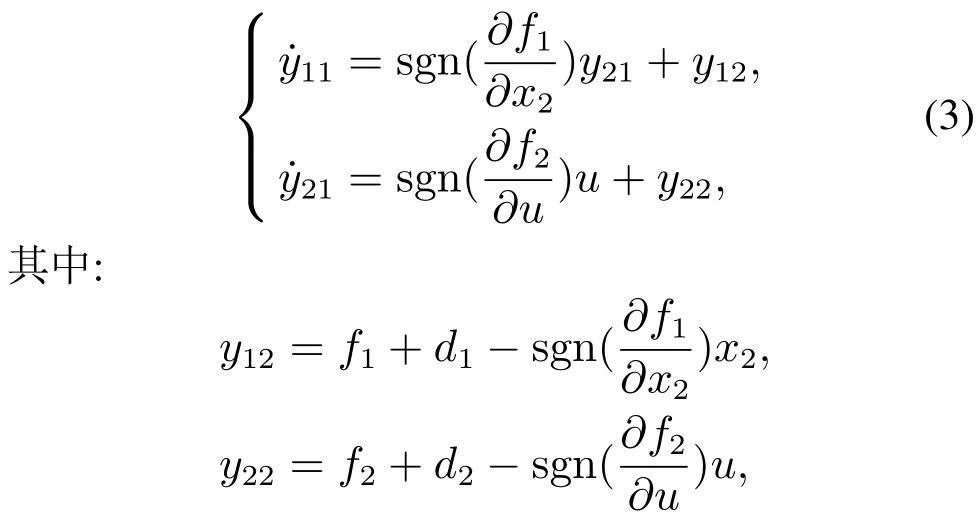
sgn(·)为符号函数.使用yi2(i=1,2)作为扩张状态,将每一阶子式扩张为一个二阶扩张状态观测器,则可获得如下系统:

可以看到,系统(4)和系统(2)是等价的,因此可以针对系统(4)进行控制系统设计,以实现对系统(2)的控制.本文通过ESO和滑模控制技术,使用系统(4)进行控制系统设计,以实现系统(2)中状态变量x1对期望信号r的跟踪.

2.2 预设性能函数

近年来提出了一种预设性能控制(prescribed performance control,PPC)[17-18],该方法通过将预设性能函数(prescribed performance function,PPF)和误差变换引入控制系统,实现了对控制系统瞬态性能的设计.经典的PPF与误差变换函数采用如下形式:

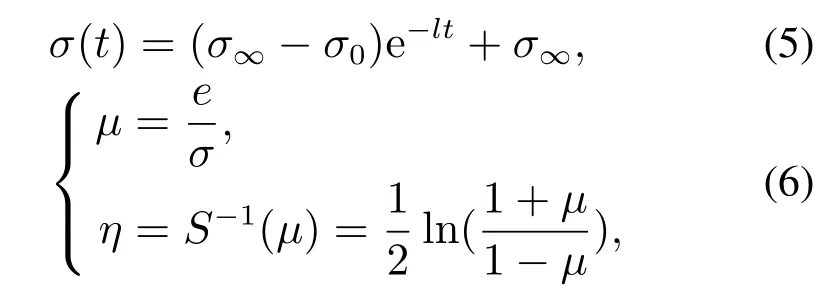
式中:σ为误差边界,即PPF,σ0和σ∞分别为边界初值及最终误差带大小;l是控制收敛速度的参数;e是系统跟踪误差;μ为中间变量;η是变换后的误差.通过对η设计合适的控制律,即可保证系统跟踪误差e满足下述约束[17-18]

式(7)表明,通过对σ的设计,可以使收敛误差同时满足稳态误差和收敛速度的要求,限制e的超调和振荡的幅值都保持在对σ的约束当中.

3 带有瞬态性能约束的改进扩张状态观测器

3.1 改进的扩张状态观测器设计

系统(4)中,每阶子系统都可以构成一个二阶ESO.利用误差变换函数S-1(·),可获得如下形式的扩张状态观测器:

3.2 扩张状态观测器收敛性分析

将式(8)-(9)改为如下误差方程:

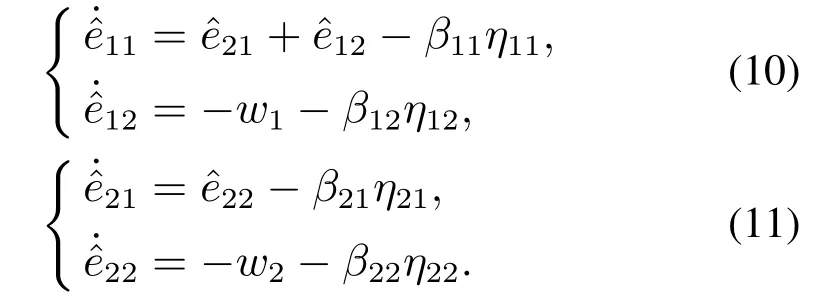
根据假设2可知,w1,w2有界,则存在不等式

3.3 滑模控制器设计

定义系统跟踪误差e=x1-r,设计如下形式滑模面:

其中:k11＞0,k12＞0,1＞ε ＞0.利用观测器(8)可获取y12的估计,代入式(12)得

z12中包含非匹配干扰d1的估计,起到了干扰观测的作用.相比只使用x2代替的方法,降低了式(12)的不确定性,提高了跟踪误差e的收敛精度.

3.4 滑模控制器稳定性分析

步骤1滑模面收敛性分析.

的解.因此,当k2≥0.5Ns时,控制律(17)可以使滑模面(12)收敛至[-smin,smin].

本文所提的控制律(17)未采用符号函数-sgn(s)克服不确定项Ns.通过式(13)可知,使用z12替代y12时将存在估计误差.即使s=0,仍不能保证跟踪误差e收敛至0.因此本文未在控制律设计中增加克服不确定性的鲁棒项,而是将smin的影响转移到式(13)中,和估计误差的影响一同处理.这样可以降低控制律(17)的复杂度,也回避了滑模面s的高频振荡问题.

步骤2跟踪误差收敛性分析.

既e≤e2,∀t≥0,补 偿 项k12tanh使得跟踪误差e的收敛速度更快.此外,在k11相同的条件下,该项使得跟踪误差有更小的收敛区间,提高了控制精度.

4 仿真验证

例1考虑如下二阶SISO非仿射系统:

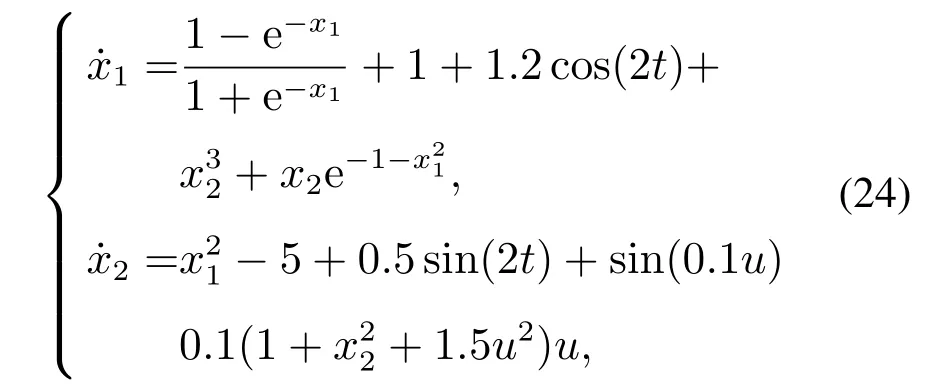
其中:x10=-3,x20=-3,期望信号r=3.

对系统(24)建立如下改进ESO:

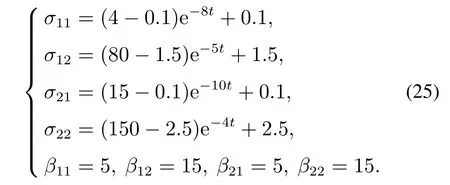
˙y11和˙y21通过如下有限时间跟踪微分器[19]获取

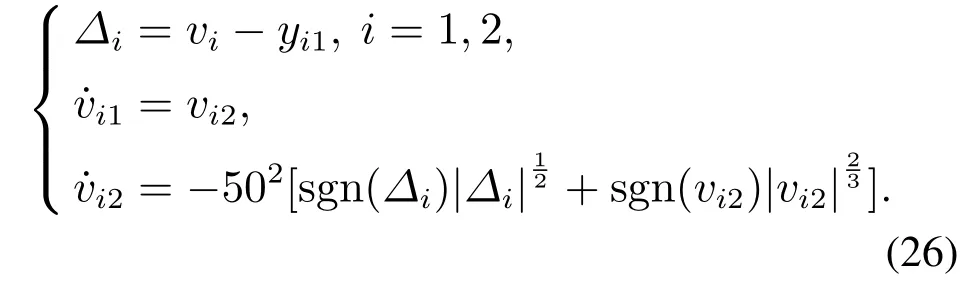
同时,仿真采用如下形式的线性扩张状态观测器(linear extended state observer,LESO)[19]作为对比

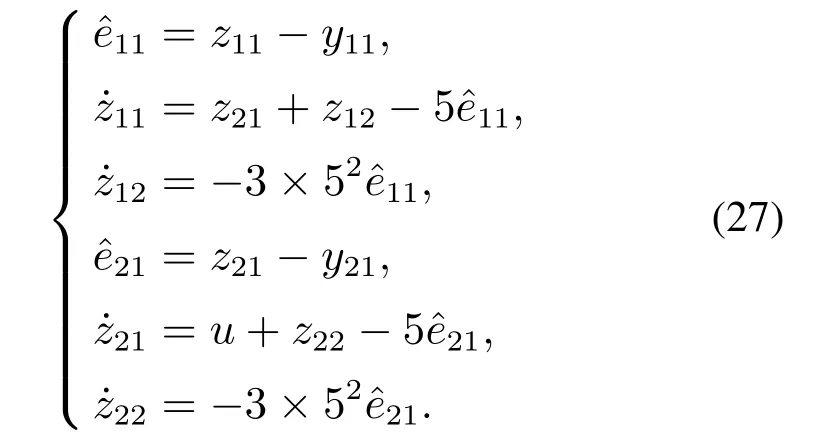
改进的滑模控制律如下:

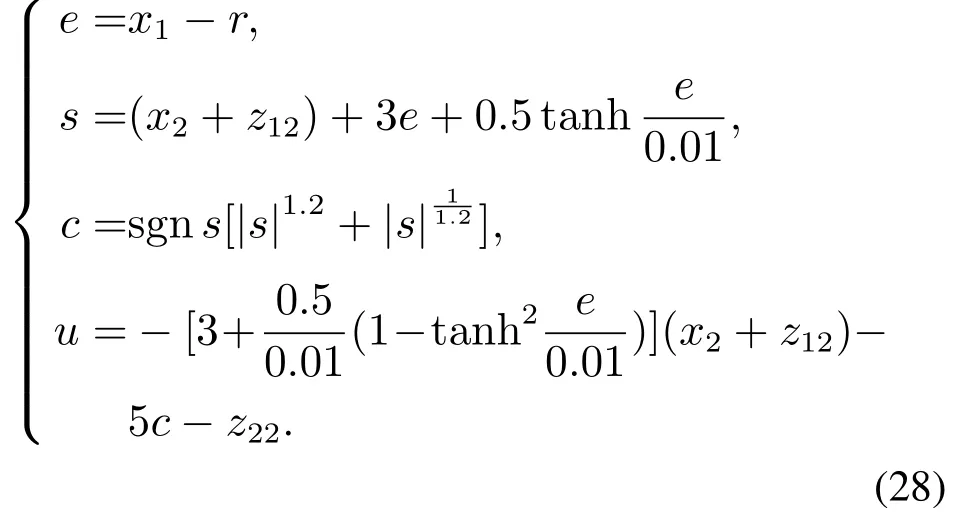
并采用如下不包含补偿项的SMC[20]作为对比:

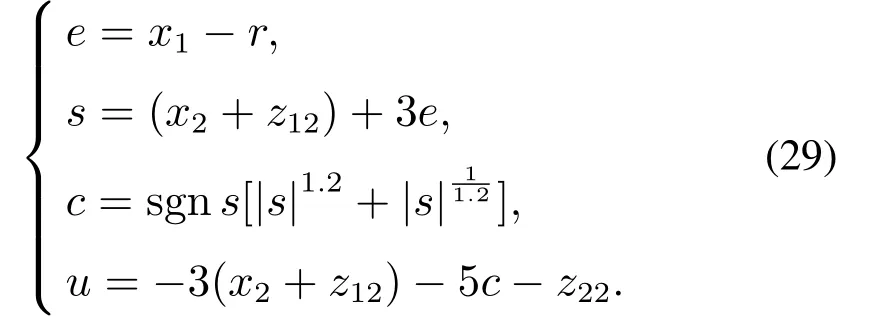
为了避免状态观测器的峰化现象导致的控制系统发散[15],本文对控制输入u进行限幅处理,保持|u|≤20.

仿真结果如图1-7所示.

图1-4给出ESO的估计结果的对比.可以看到,改进ESO的收敛速度显著快于LESO.即使进入稳态阶段,改进ESO的估计误差也明显小于传统的LESO.而图3显示,LESO的估计误差在1 s～2 s阶段甚至不能满足约束边界.而改进ESO则可以将误差保持在设计的约束边界内.

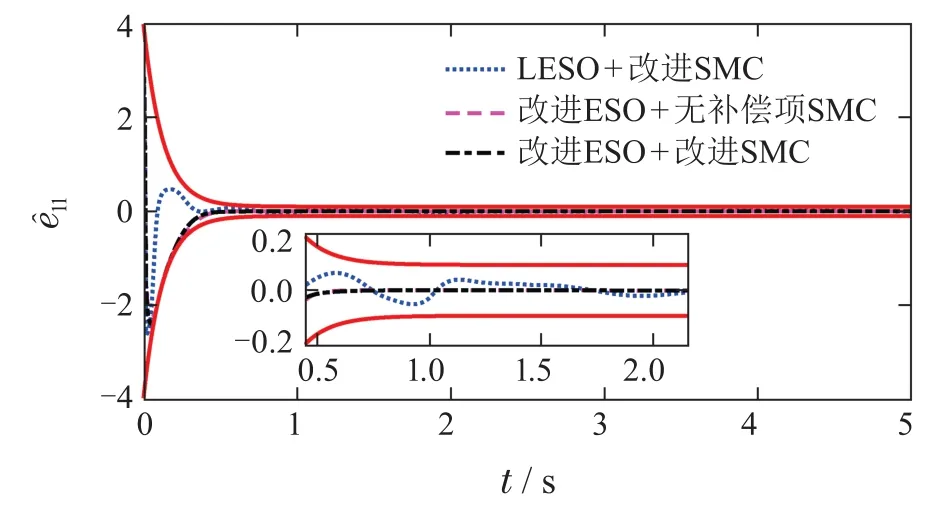
图1 x1估计误差Fig.1 Estimated error of x1

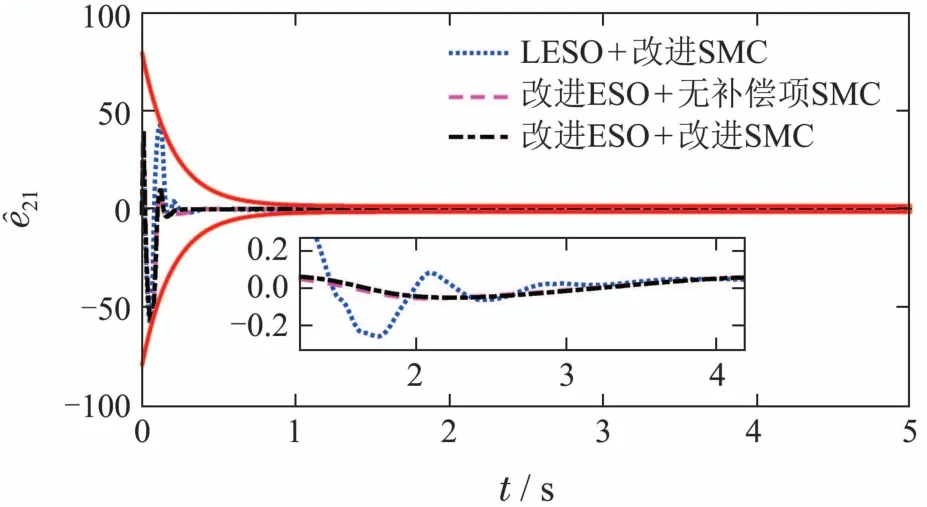
图2 x2估计误差Fig.2 Estimated error of x2

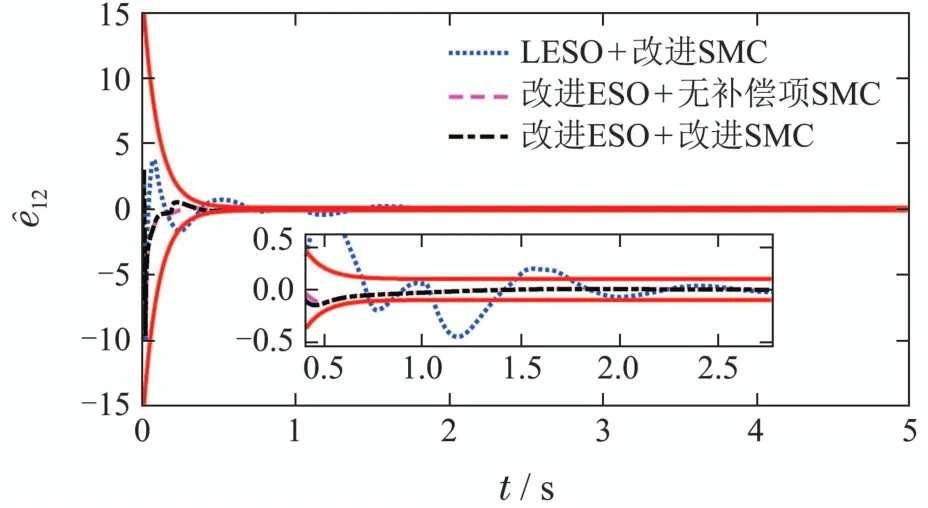
图3 y12估计误差Fig.3 Estimated error of y12

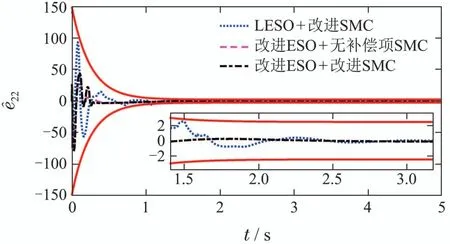
图4 y22估计误差Fig.4 Estimated error of y22

图5 指令跟踪曲线Fig.5 Tracking curve

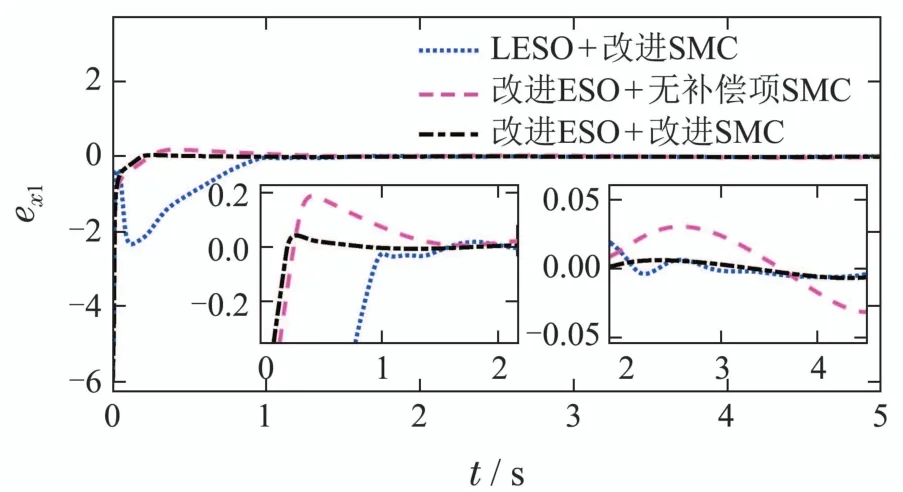
图6 指令跟踪误差Fig.6 Tracking error

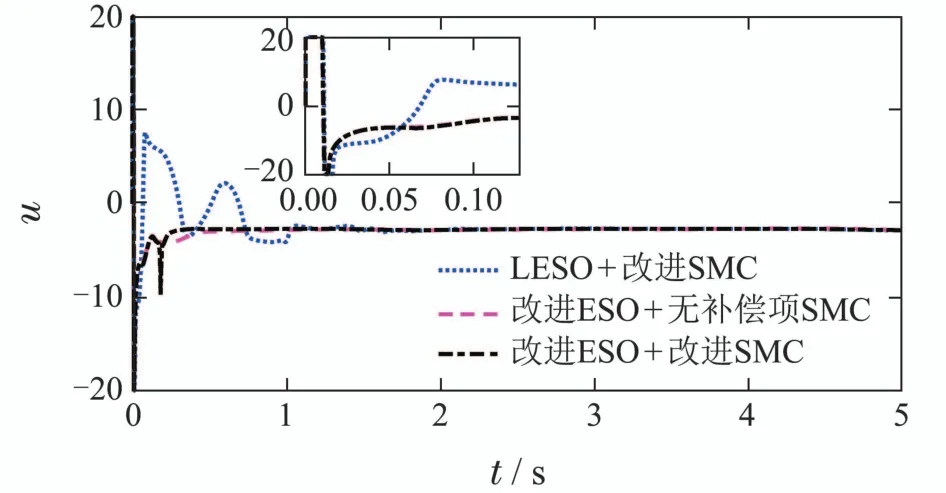
图7 控制输入Fig.7 Control input

图5-7给出了控制系统的仿真结果.可以看到,由于改进ESO改善了估计过程的瞬态响应,降低了超调,减少了振荡,使得控制系统在实现信号跟踪时获得更平滑的输出.在初始的0.5 s内,LESO的估计误差还在大幅振荡,而改进ESO已经缓缓收敛至0.而在此时段内,采用LESO的控制系统也受到估计结果的影响.跟踪误差在接近0后又出现一个扩大趋势,然后才缓慢收敛,大大增加了系统的调节时间.

另一方面,图6显示了SMC中补偿项的改进作用.包含补偿项的SMC能够更快的收敛,并且在稳态区间也有着更小的跟踪误差.

例2将本文所提方法应用在超声速飞行器纵向面姿态控制当中.对某超声速飞行器攻角调节过程进行数值仿真.简化飞行器动力学模型如下[21-22]:

可以看到,飞行器的气动参数是飞行状态的复杂非线性函数.当气动参数非线性很强时,线性化处理会产生较大的模型偏差.对系统(30)建立如下改进ESO:

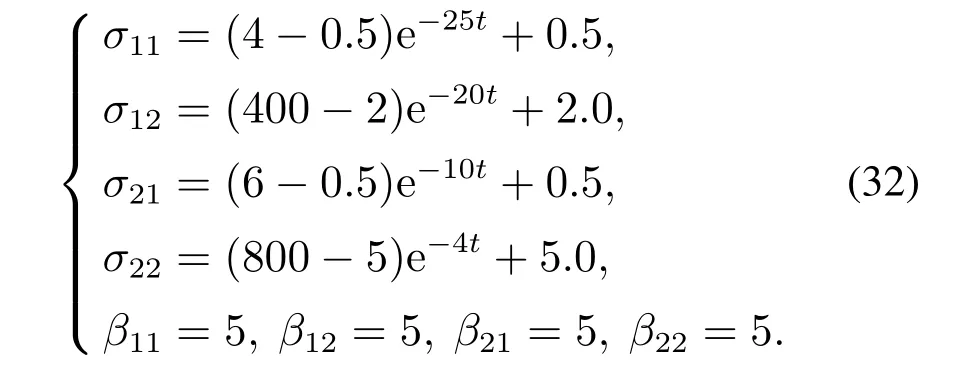
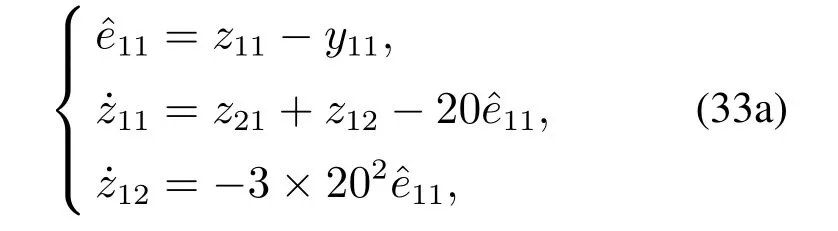
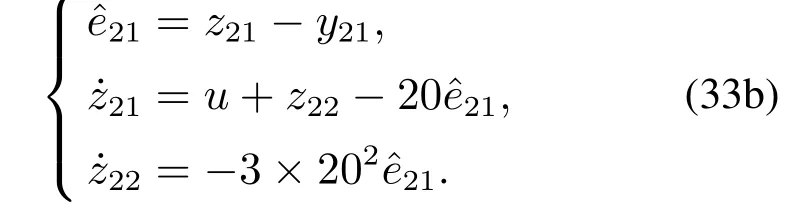
改进的滑模控制律如下:

仍然添加不包含补偿项的SMC参与对比,舵偏δz也进行限幅,保持|δz|≤25°.

仿真结果如图8-15所示.

图8 攻角估计误差Fig.8 Estimated error of angle of attack

图9 俯仰角速度估计误差Fig.9 Estimated error of pitching rate

图10 y12估计误差Fig.10 Estimated error of y12

图11 y22估计误差Fig.11 Estimated error of y22

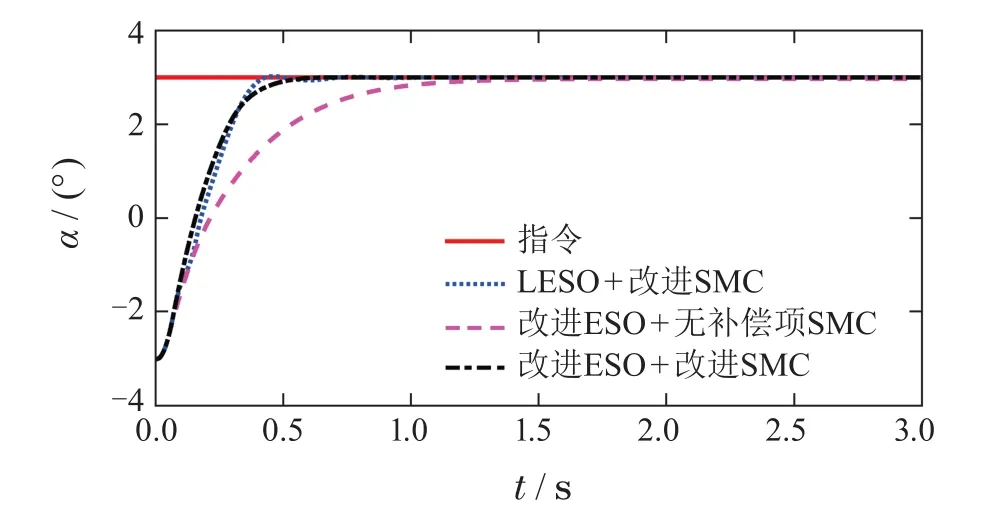
图12 攻角跟踪曲线Fig.12 Tracking curve of angle of attack

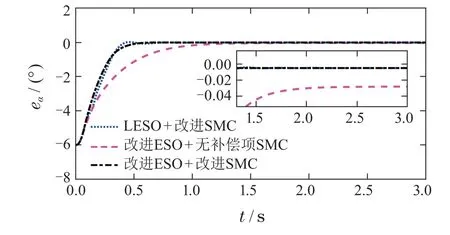
图13 攻角跟踪误差Fig.13 Tracking error of angle of attack

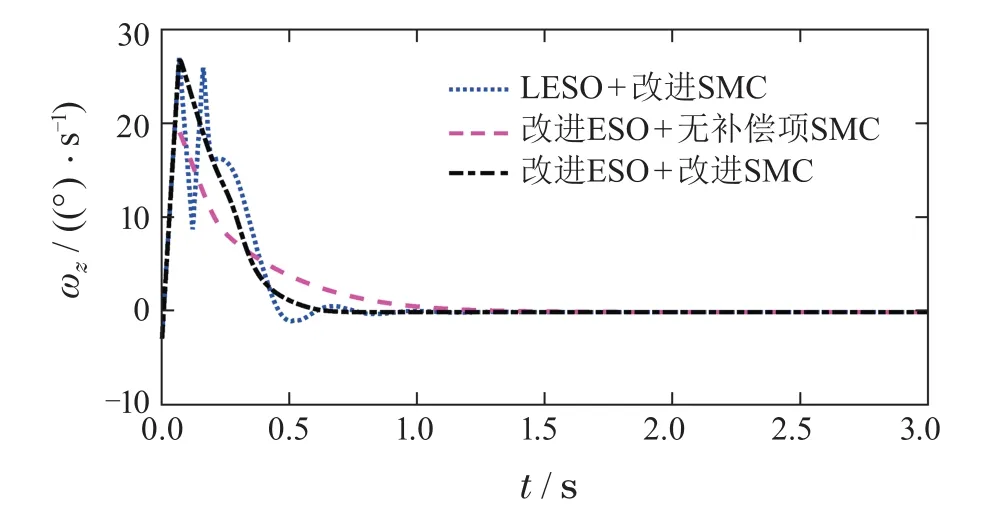
图14 俯仰角速度响应Fig.14 Response of pitching rate

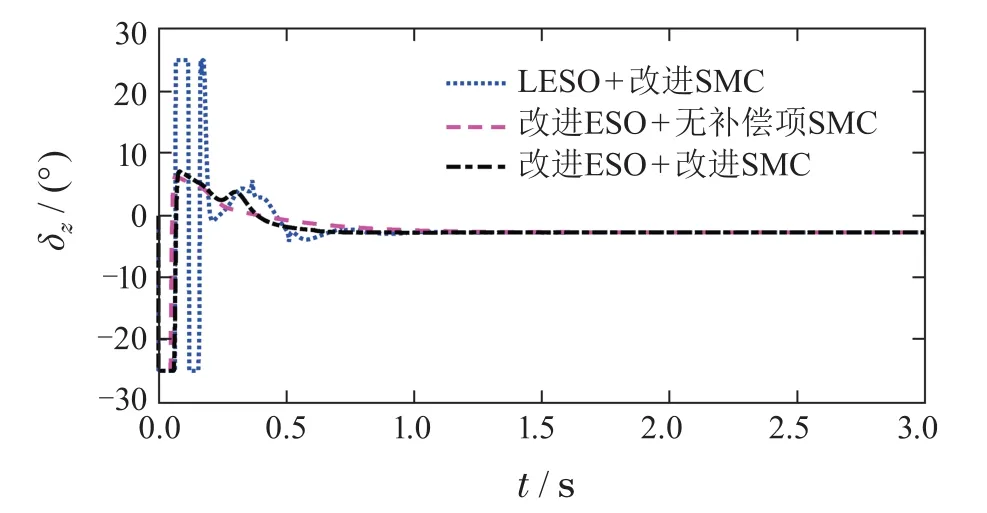
图15 俯仰舵偏曲线Fig.15 Elevator deflection

图8-11给出ESO的估计结果的对比.可以看到,改进ESO的瞬态性能表现仍然优于LESO.除角速度估计误差外,其他估计误差均不能满足约束边界.y12和y22的估计误差则在瞬态出现了幅值较大的振荡现象,并对控制系统造成了明显影响.

图12-15给出了控制系统的仿真结果.由于LESO瞬态过程存在大幅值的振荡,使得舵偏在初始0.3 s内触发限幅,反复出现满偏振荡现象.这对超声速飞行器的控制而言是绝对不希望出现的.而改进ESO在初始的尖峰现象结束后,估计误差就快速收敛到0.因此,俯仰舵偏只出现一个短暂的满偏,之后就进入平稳变化阶段,并没有出现振荡现象.图13展示出补偿项的改进效果.包含补偿项的SMC在0.5 s既完成收敛,最终的稳态误差也明显小于无补偿的方法.

5 结论

本文所提的改进ESO将非仿射系统转换为积分串联形式,并采用ESO进行估计,不需要对象模型的确切已知.预设性能函数能够明显减少ESO瞬态过程中的超调和振荡次数.同时估计结果包含了非匹配的外部扰动,使得所提的控制方案能够利用估计结果处理非匹配干扰,提高控制精度.而所提的SMC方案在滑模面设计中添加了补偿项,提高了SMC的收敛速度,减小了稳态误差,降低了ESO估计误差对控制系统的影响.此外,利用ESO的估计将未知非仿射系统变形为一个已知的仿射系统,克服了SMC在应用时需要模型已知或部分已知的问题,拓宽了SMC的应用范围.因此,本文所提的基于改进ESO的SMC方案是一种解决含有非匹配干扰的未知非仿射系统跟踪控制问题的有效方法.