应用粒子群算法优化模糊规则的自适应多目标控制策略

林歆悠 王召瑞

(1.福州大学机械工程及自动化学院,福建福州 350108;2.汽车零部件先进制造技术教育部重点实验室(重庆理工大学),重庆 400054)

1 引言

为解决能源匮乏及环境污染两大突出问题,各国相继开始大力发展新能源汽车.其中,插电式混合动力汽车(plug-in hybrid electric vehicle,PHEV)作为传统混合动力汽车向纯电动汽车的过渡车型,因其具有电池容量大、可外插充电、行驶里程长等特点,是目前新能源汽车的研究开发热点之一[1].而好的能量管理策略是PHEV具有良好性能的基础,因此建立有效、合理的能量管理策略具有重要的理论和现实意义[2-4].

针对所研究目标的不同,如何最大限度的利用各动力源的优点,弥补各动力源的不足已成为评价能量管理策略优劣的重要指标[5].根据PHEV能量管理策略的实现方式,可以分为基于规则式的能量管理策略和基于优化方法的能量管理策略[6-7].基于规则的策略其阈值大多数是根据工程经验设定的,无法获得全局最优.而粒子群(particle swarm optimization,PSO)算法是一种结构简单、收敛速度较快并且能够在个体性与社会性之间寻求平衡的随机全局优化算法.如何将两者结合且运用到汽车控制中正被越来越多的学者所研究[8-11].文献[9]以电池荷电状态(state of charge,SOC)、电机转矩和整车需求功率为输入,以影响到电池SOC和电机转速以及发动机高效工作区间的两个曲线系数为输出,构建模糊控制器优化系统的燃油经济性.不过该文献并没有考虑到整车的排放性,文献[10-11]则以混合动力汽车的燃油经济性与排放性作为优化目标,利用粒子群算法对其隶属度函数值和控制规则进行优化,仿真结果表明,通过优化其油耗及排放均得到有效改善.

为了使汽车的控制策略能够在线实时地运用到整车控制中,越来越多人倾向于选择基于瞬时的优化方法.其中最典型的是等效油耗最小策略(equivalent consumption minimization strategy,ECMS).ECMS的核心是将电能消耗通过等效因子转化成燃油消耗,然后在每个瞬时时刻选择等效油耗最小的工作点作为当前工作点,实现动力系统功率的合理分配[12].由于当行驶工况以及车辆状态变化时,对应的最优油电等效因子是不同的,故需要依据行驶工况及车辆状态的变化来动态地改变等效因子,这便产生了自适应等效油耗最小能量管理策略[13-15].文献[13]利用神经网络规划出一条参考电池SOC轨迹与反馈的SOC共同作用于等效因子,从而实现等效因子的动态调节,获得全局范围内最优的发动机和电池能量分配,但它并没有考虑比例积分(proportional integral,PI)系数对于等效因子的影响.文献[14]则利用模糊PI控制器来动态调整等效因子,仿真结果表明与传统的ECMS相比其鲁棒性与燃油经济性都有明显的提高.文献[15]是以两个公交站牌为一部分将一段行驶里程分割成几部分,利用PSO算法来优化不同里程及不同SOC情况下各部分的等效因子,将优化结果转化为一张MAP用以实时控制.

为了改善一款插电式混合动力汽车的燃油经济性和排放性,本文建立了基于油耗和排放优化的多目标优化控制策略.为优化自适应等效油耗最小控制策略的控制效果,首先利用模糊比例积分来构建等效因子优化模型;随后利用粒子群优化算法优化模糊隶属度函数参数和模糊控制规则,以此来得到更为准确的比例和积分系数用于调整等效因子以分配整车动力.基于此,便形成了基于PSO-fuzzy的PHEV等效因子自适应的多目标优化控制策略.

2 PHEV动力系统结构及工作模式划分

2.1 车辆动力系统结构与建模

本文研究一款插电式混合动力汽车,其动力系统的结构如图1所示,主要部件包括发动机、动力电池、集成启动(integrated starter/generator,ISG)电机、离合器、电动机、无级变速器(continuously variable transmission,CVT)和整车控制器等.

图1 混合动力系统结构Fig.1 Hybrid electric power-train system structure

发动机燃油消耗率与转矩和转速之间的关系采用数值插值法构建,所得三维MAP如图2所示.由此,发动机的燃油消耗量Q可以表示为

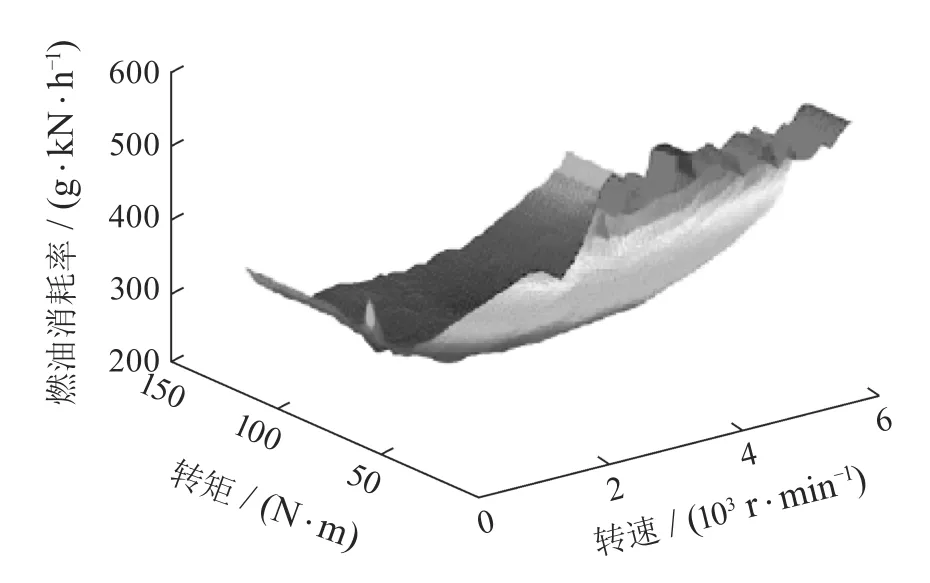
图2 发动机油耗数值模型Fig.2 Engine fuel consumption model

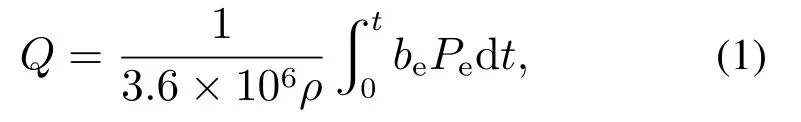
式中:ρ为燃油密度,be为燃油消耗率,Pe为发动机输出功率,t为时间.

混合动力汽车的电机既可以提供车辆行驶时所需要的驱动力,也可以将制动能量传递至蓄电池为其充电.电机在驱动和制动模式下的效率可以通过图3所示的效率图插值求得,即

图3 电机效率数值模型Fig.3 Motor efficiency model

式中:ηm为电机效率,nm为电机转速,Tm为电机转矩.

锂离子电池具有高能量比、循环寿命长等优势,作为本文蓄电池的选型.蓄电池的模型通过等效电路法获得,其输出电压Ub和电流Ib为

式中:Uoc为电池开路电压,Rb为电池内阻,Pb为电池功率.此外,式中的SOC均简写为S.

由式(3)可以看出,电池内阻和电池开路电压都是电池SOC的函数,SOC的计算为

式中:SOC0为电池SOC初始值,Qb为电池容量.电池效率与SOC和功率的关系如图4所示.

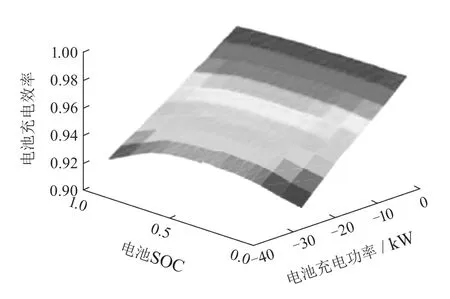
图4 电池充/放电效率数值模型Fig.4 Battery charging/discharging efficiency model

2.2 车辆工作模式划分与切换策略

基于该款汽车传动系统的结构特点,在其实际运行过程中根据动力源的具体工作状态,可以划分为5种不同的工作模式:纯电动、发动机单独驱动、行车充电、混合驱动和再生制动模式.

为提高各动力传动部件的效率,本文针对不同的工作模式,通过获取CVT最优速比和电机目标转矩来优化系统效率.以纯电动模式为例,此模式下传动系统的效率为

式中:ηsys为系统效率,Pin为系统输入功率,Pout为输出功率.

传动系统的输入功率和输出功率分别为

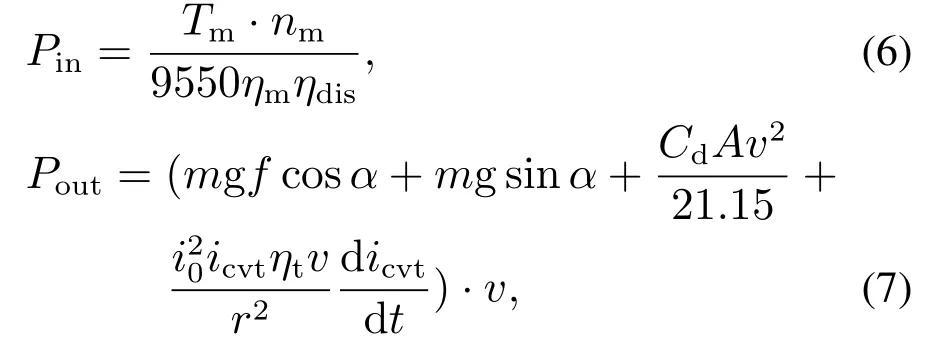
式中:ηdis为电池放电效率,m为整车质量,α为道路坡度,Cd为空气阻力系数,A为迎风面积,v是车辆行驶速度,i0为主减速器传动比,icvt为CVT传动比,r为车轮半径.

结合式(5)-(7),系统效率优化目标函数为

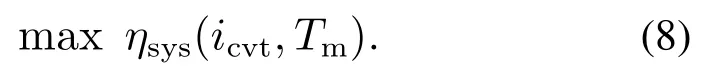
通过上述方法,求得纯电动模式下最优CVT速比MAP和电机目标转矩MAP以及最优系统效率MAP如图5所示.

图5 纯电动模式最优系统效率MAPFig.5 Optimal system efficiency map under EV mode

将各个模式下的最优系统效率MAP放置到同一个三维坐标空间中,选取各个速度和加速度组成的坐标对应下使系统效率处于最大值的曲面.这样,不同工作模式最优系统效率MAP之间会产生多条交线,将交线水平投影到由速度和加速度构成的平面上,即可得到驱动时各个模式之间切换的边界线,如图6所示.

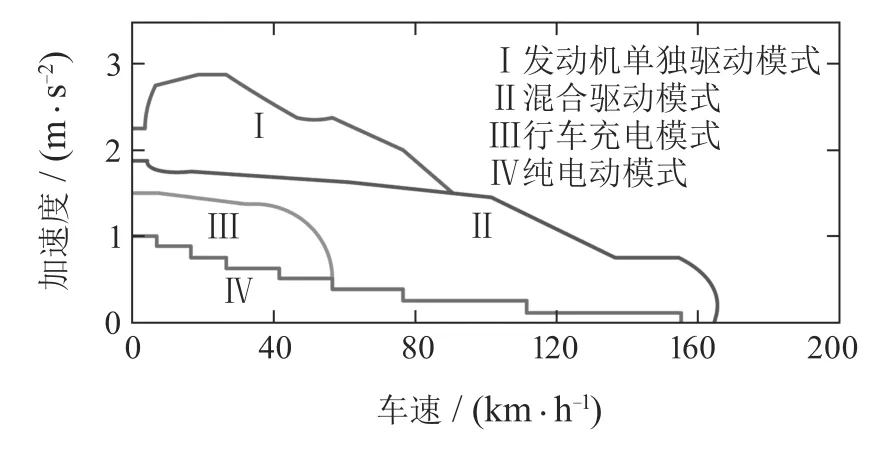
图6 驱动模式切换边界线Fig.6 Switch boundary lines of drive modes

由此建立了混合动力汽车的工作模式切换策略.该策略根据车速及其加速度确定能使混合动力汽车处于系统效率最优状态下的工作模式,而各工作模式下具体的能量分配将在下一部分进行描述.

3 多目标优化控制策略

随着相关法律和法规对汽车环保性能提出越来越高的要求,本文综合考虑混合动力汽车的燃油经济性及其排放性能来建立多目标优化控制策略,来合理分配PHEV 各动力部件之间的能量.燃油经济性的指标为整车的燃油消耗量,排放指标设置为HC,CO 和NOx的排放量.由此,建立所要优化的价值函数J(u(t),t)如下:

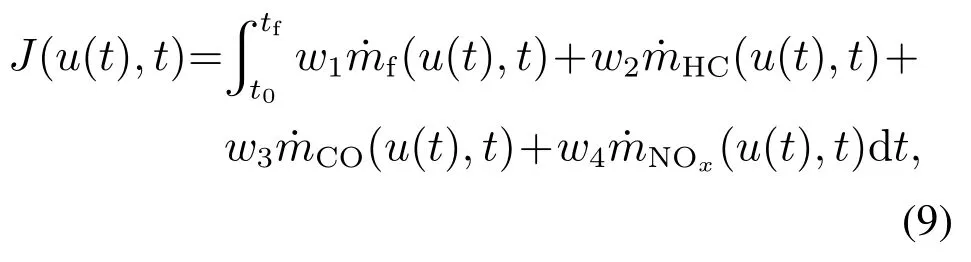
式中:u(t)=[Tene]为控制变量,Te和ne分别为发动机的转矩和转速,为瞬时燃油消耗率,表示发动机瞬时HC排放率,表示瞬时CO排放率,表示瞬时NOx排放率,w1,w2,w3和w4分别为权重因子,t0和tf分别为行程初始时刻和终止时刻.

对于本文所研究的插电式混合动力汽车而言,在某些情况下需要消耗燃油来维持电池的SOC值.因此采用ECMS方法将发动机的实际油耗和电池的等效油耗两部分之和作为最终的燃油消耗量,其计算为

初始等效因子s(t)的取值如下:

式中:ηchg为电池充电效率,分别为发动机、电机和ISG电机的平均效率.

油耗、HC排放、CO排放和NOx排放4个优化子目标之间不可避免地存在着互斥关系,使得全部优化目标难以同时实现.因此在解决多目标优化问题时,需要依赖决策者对整车燃油经济性和排放性的偏好程度来设置各子目标所占权重.本文将油耗优化和3种尾气排放量优化视为同样重要的优化目标,故各权重因子之间的差值不应过大.此外,通过对比图7中各污染物排放数据,可以发现CO的排放速率明显快于另外两种排放物.为了遵循各排放优化目标同等对待的原则,将CO排放优化子目标的权重因子适当调低.本文通过设置多组符合上述规则的权重因子,以价值函数的值作为权重因子选取的评判标准.最后,选取一组较优的结果作为最终的权重因子取值,分别为w1=0.3,w2=0.3,w3=0.1和w4=0.3.

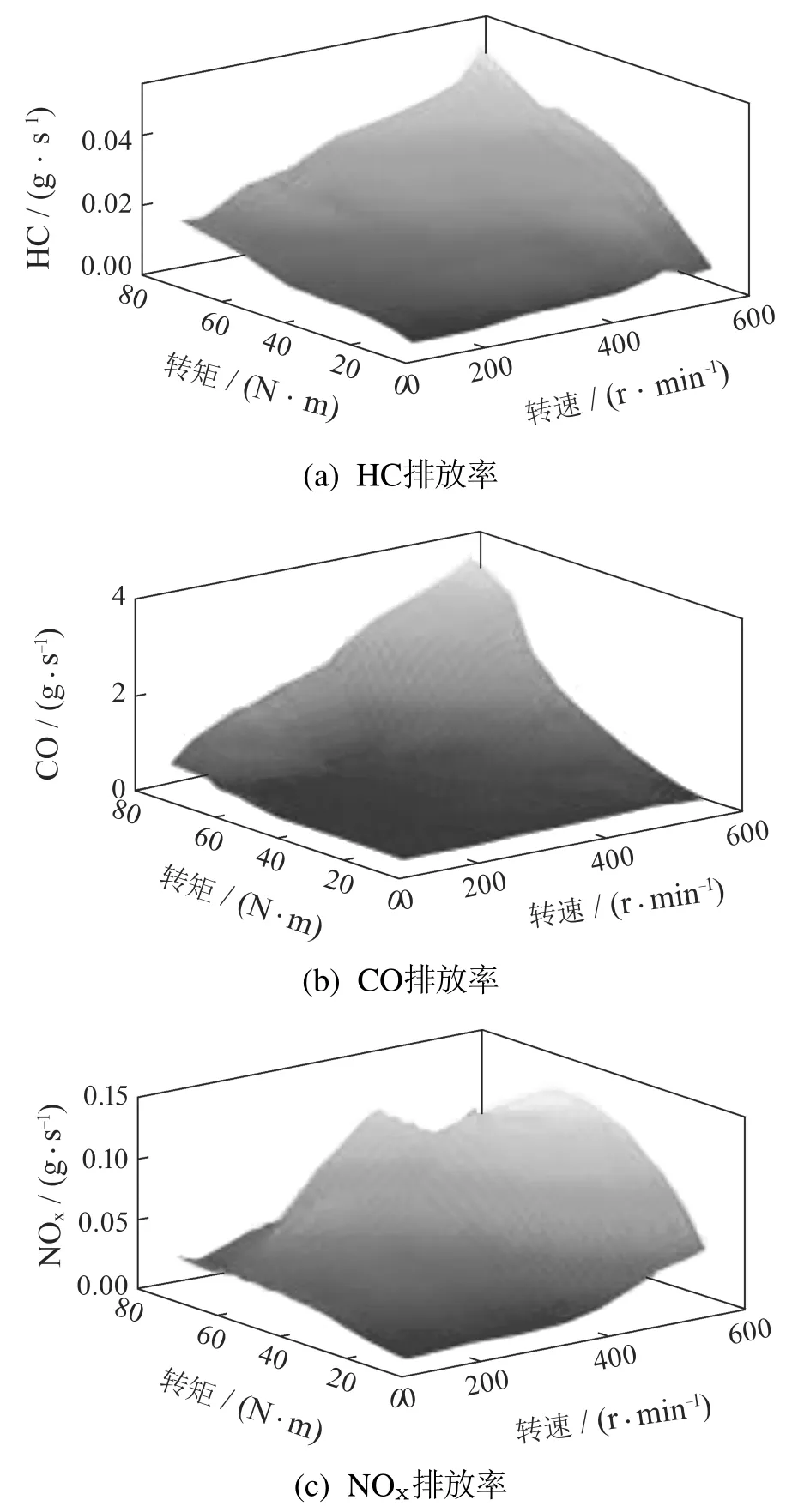
图7 不同发动机转速和转矩下的3种污染物排放率Fig.7 Emission rates of the three kind of pollutants at different engine speeds and torques

于是,本文基于权重分配的多目标优化问题便可转化成单一目标函数优化,目标函数为

式中f(u(t),t)表示燃油消耗率及各污染物排放率与控制变量之间的函数关系.为了便于控制策略的在线实施,上述函数关系分别根据图2和图7通过插值方法获得实时油耗和排放,以简化计算过程的复杂程度.

4 PSO-fuzzy等效因子优化模型

对于上述多目标优化问题,关键是找到最佳的等效因子s(t),获得电池与发动机能量的实时最佳分配.此外,等效因子随时间变化,如何实时确定等效因子将直接影响到整车的经济性能和排放性能.基于此,为获得较准确的等效因子,本节建立基于PSO-fuzzy的等效因子优化模型.

4.1 等效因子优化模型建立

将式(10)使用庞特亚金极小值原理构建Hamilton函数为

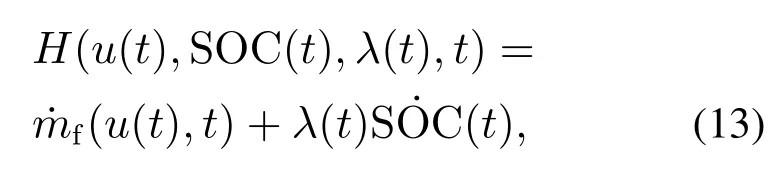
式中λ(t)为拉格朗日乘子.为方便表达,下文中的H(u(t),SOC(t),λ(t),t)统一简化为H.

根据极小值原理,λ(t)的正则方程表示为

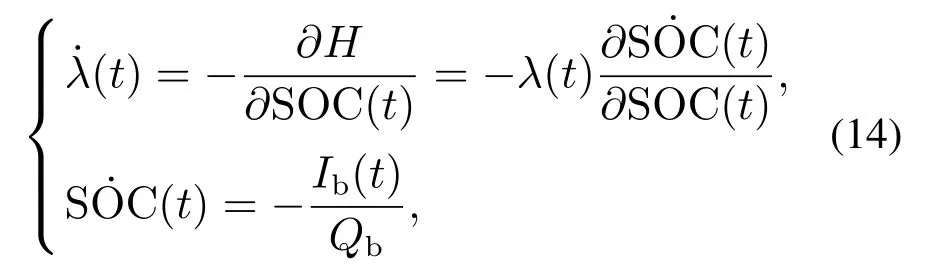
电池功率Pb的计算为

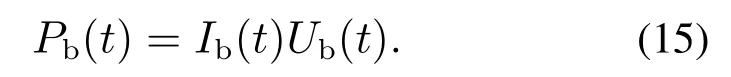
结合式(14)-(15),式(13)可以改写为

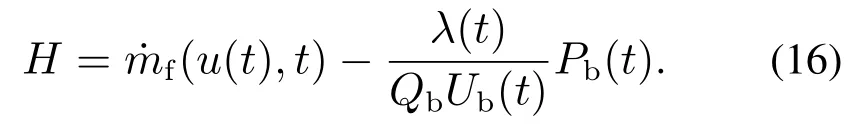
于是结合式(10)与式(16),可将等效因子表示为

为保证电池充电的可持续性,结合参考SOC[16]与实时SOC对SOC进行惩罚,目标函数式(10)可改写为

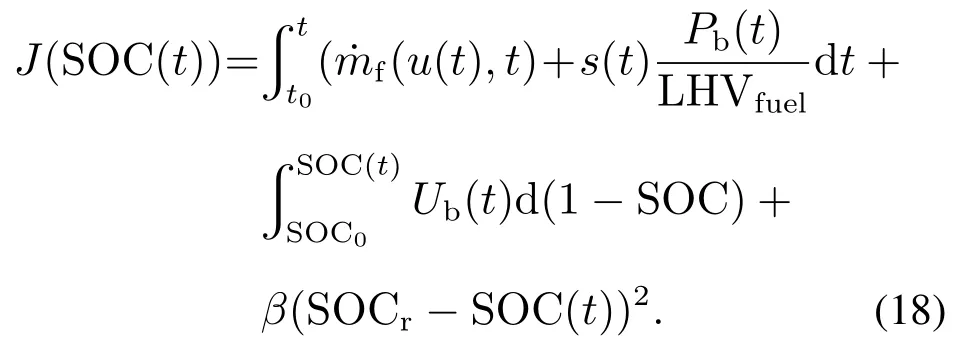
价值函数(18)等号右半部分,第1项为燃油消耗产生的价值,第2项为油耗转化为电能产生的价值,其余项为SOC的惩罚函数,为了保证电池充电的持续性而产生的价值.结合式(18),根据哈密顿-雅可比-贝尔曼方程,最优的拉格朗日乘子λ*(t)可由下式得出:

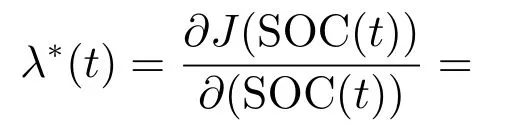
结合式(17)与式(19),等效因子可表示为

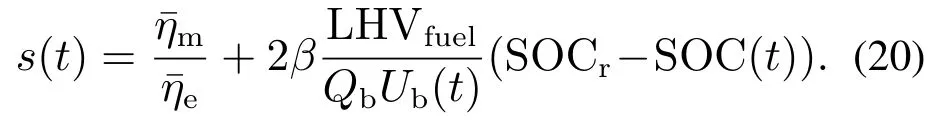
将上式用更为精确的PI控制器控制,如下式所示:

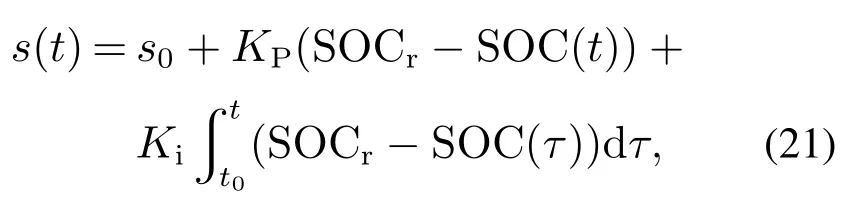
式中:s0为初始值(常数),Kp和Ki分别为PI控制器的比例系数及积分系数.

4.2 模糊控制器设计

为提高充电可持续性和燃油经济性,需要对等效因子进行实时在线调整.鉴于此,本文提出一种基于模糊PI控制器的新的自适应律:将参考SOC与实时SOC的差值ΔSOC及其变化率dSOC作为模糊控制器的输入,通过对2个输入信号模糊化运算,由模糊规则进行模糊推理,最后解模糊化处理得到Kp和Ki系数两个输出.由于三角形隶属度函数灵敏度高且运算简单,故输入输出均采用三角形隶属度函数,并且定义语言变量的名称分别为“负大(NB)、负小(NS)、零(ZR)、正小(PS)和正大(PB)”.由仿真模型运行得知,输入输出的范围分别为[-0.1,0.1]和[-3.8,3.8].

等效因子可以认为是对电能“价格”的调控:如果等效因子过大,混合动力汽车倾向于消耗更多的燃油,此时可认为电能价格相对昂贵;反之,混合动力汽车倾向于使用电能,此时的电价相对便宜.依此推理,当ΔSOC＞0时,即实际SOC小于参考SOC,此时应该使电池电量消耗的慢些,应该多使用燃油,即等效因子应变大;当ΔSOC＜0时,实际SOC大于参考SOC,应该多使用电能,即等效因子应变小.又因为等效因子与Kp和Ki成正比,并且由于PI的特性,Kp对等效因子的影响大于Ki对等效因子的影响.同理dSOC的变化与ΔSOC类似,因此制定如表1-2所示的模糊控制规则.

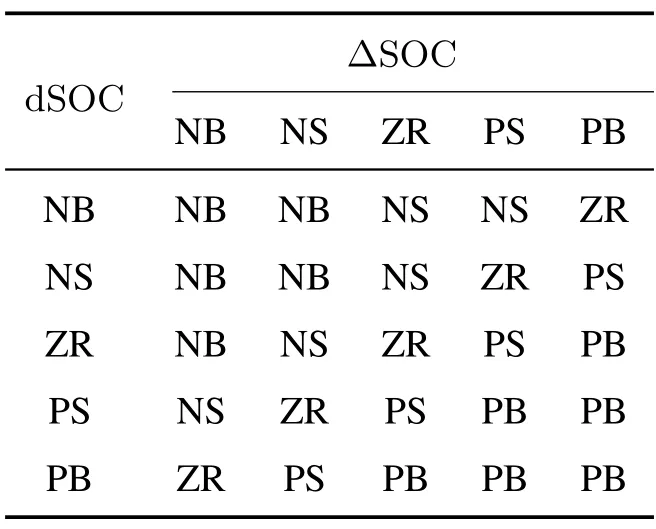
表1 Kp的控制规则Table 1 Control rules of Kp

表2 Ki的控制规则Table 2 Control rules of Ki

4.3 基于PSO的模糊逻辑规则优化

上述内容利用模糊控制器调整Kp和Ki来调节等效因子,但不能保证控制效果.在这一章节,采用PSO算法来优化模糊控制器的隶属度函数值及模糊规则,得到较佳的等效因子用于整车的能量分配,从而建立起自适应多目标优化控制策略.

将PSO算法运用到隶属度函数和控制规则中的前提是对二者进行编码,由于两输入与两输出的范围分别为[-0.1,0.1],[-3.8,3.8],即其模糊子集是关于论域中心对称,故输入需要确定的优化参数为x1,x2,x3,x4和x5,输出需要确定的优化参数为x6,x7,x8,x9和x10,故需要优化确定的论域参数为10个,即粒子群位置参数的维数为10维.关于PSO算法的具体介绍,可以参考先前研究文献[11],在此不做赘述.

由于文章篇幅有限,此处以输入dSOC和ΔSOC,输出Ki为例,展示PSO算法优化前后的输入及输出规则变化.两个输入变量的规则变化如图8所示,而输出变量的规则变化如图9所示.

图8 PSO优化前后输入ΔSOC和dSOC的规则图Fig.8 Rules of inputs before and after PSO optimization

图9 PSO优化前后输出Ki的规则图Fig.9 Rules of output before and after PSO optimization

5 验证及结果分析

为验证所提出的基于PSO-fuzzy的PHEV等效因子自适应多目标优化控制策略的有效性,本文采用福州市实际行驶工况数据对其进行仿真验证.该仿真工况根据不同的交通状况分为5段,如图10所示,并将该实际综合工况的2倍长度作为本次验证的运行工况.

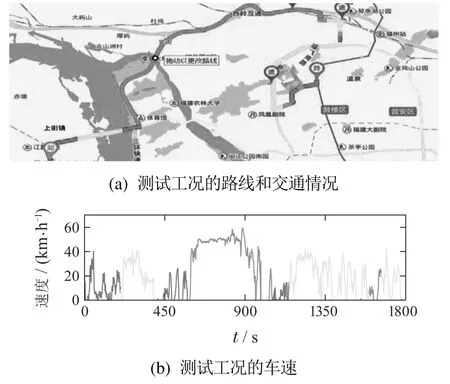
图10 福州市实际行驶工况数据Fig.10 Data of actual driving cycle in Fuzhou city

在福州市实际工况下,PSO算法的输入ΔSOC和dSOC以及输出的优化后的模糊控制器Kp和Ki系数如图11所示.可以看出,在设定的范围内,随着输入的不断变化,PSO算法能够实时优化控制器的Kp和Ki系数.

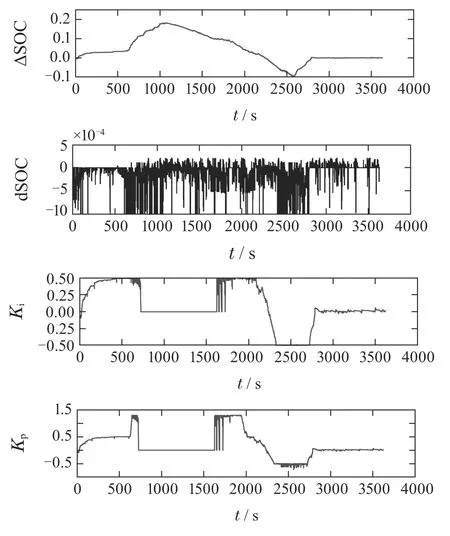
图11 PSO算法优化结果Fig.11 Optimization results by PSO algorithm

随后,将采用PSO-fuzzy优化的等效因子结合到本文提出的多目标优化控制策略与未采用PSO优化的基于模糊规则控制等效因子的多目标优化控制策略进行对比仿真以验证本文方法的优越性.图12对比了在两种控制策略下的SOC轨迹和等效燃油消耗量.由图可知,当等效因子经PSO优化后,SOC轨迹的变化范围缩小,即优化后的控制策略能够在一定程度上避免电池过度放电,从而更能保护电池.此外,经过PSO优化后的等效油耗为7.75 L,相比未经PSO优化的等效油耗8.52 L,燃油经济性提高了9.0%.因此本文所提出的控制策略优化效果较为显著.

图12 PSO优化前后的SOC等效油耗变化曲线Fig.12 SOC change and equivalent fuel consumption curves before and after PSO optimization

图13为两种策略控制下的发动机,电机及ISG电机的转矩工作曲线对比结果.从图中可以看出,在整段行驶工况的后半段,由于剩余电量的减少,基于一般模糊规则调整等效因子的控制策略更为频繁地使发动机及ISG电机参与工作.而经过基于PSO优化模糊规则来调整等效因子的控制策略则减少了发动机及ISG电机的工作,更多地利用电能来满足工况的需求,以此来调节发动机的输出转矩,从而提高发动机的燃油经济性.

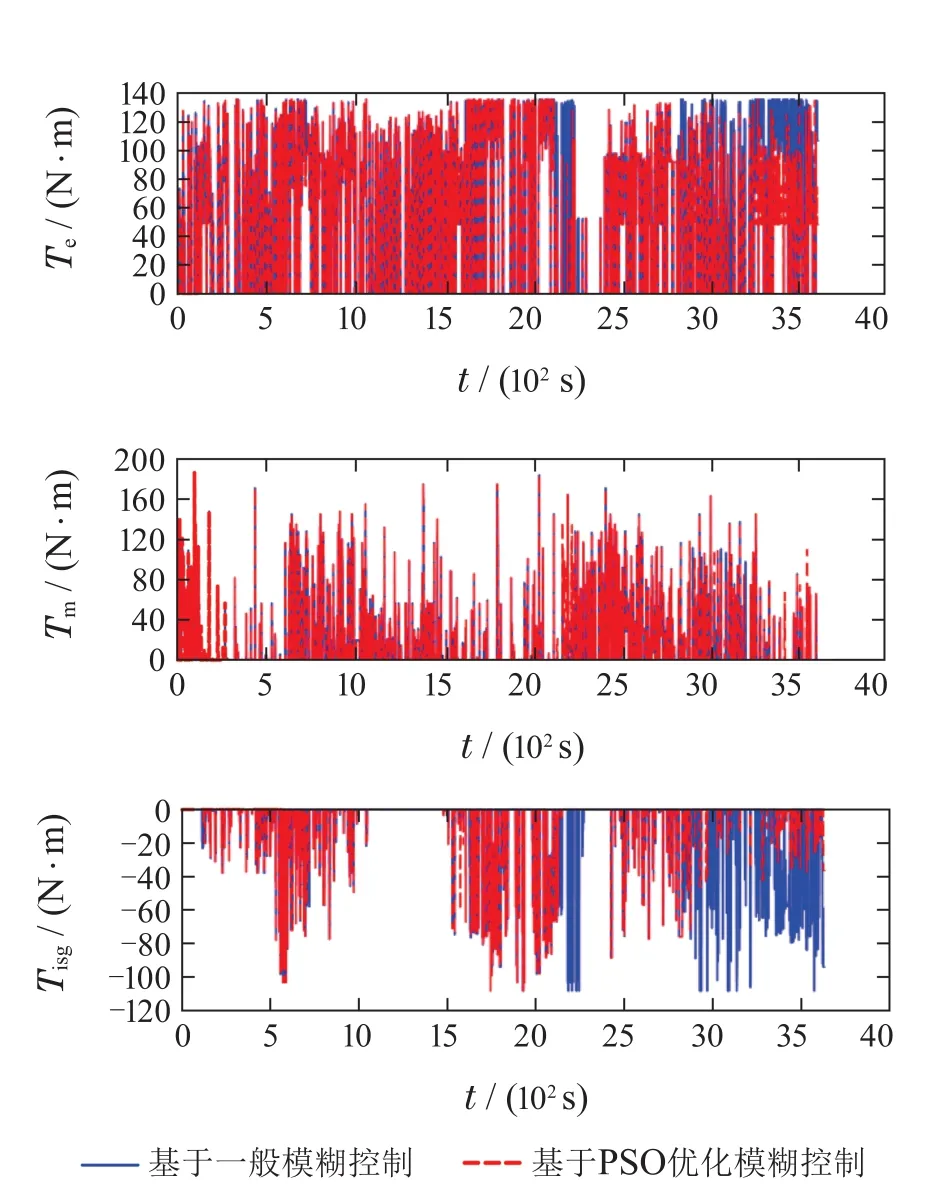
图13 转矩工作曲线对比Fig.13 Comparison of torque working curves

图14对比了两种策略控制下的排放性结果.由图可知,整个仿真工况中,在基于PSO-fuzzy的等效因子自适应多目标优化控制策略下,PHEV的HC、CO和NOx排放量相比于采用一般模糊规则的控制策略均有一定程度的改善.其中,HC排放量降低了2.7%,CO排放量降低了2.9%,NOx的排放量降低了7.8%.

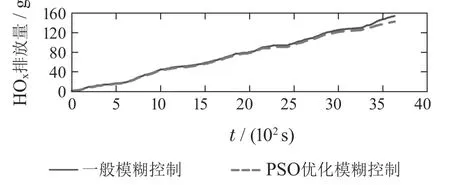
图14 排放性优化结果对比Fig.14 Comparison of emission optimization results

6 结论

本文以一款插电式混合动力汽车为研究对象,建立了以等效因子为核心的综合油耗优化与排放性优化的多目标优化控制策略.为了获得较为精确的等效因子用于动力部件之间的动力分配,利用模糊比例积分构建了等效因子优化模型,并利用PSO算法优化模糊隶属度函数参数和模糊控制规则.最后,在福州市实际行驶工况数据下对本文所提出的等效因子自适应多目标优化控制策略进行了仿真验证.仿真试验结果表明,所提出的控制策略使得PHEV的燃油经济性和排放性得到了明显改善.经过PSO算法优化的模糊控制策略与一般模糊控制策略相比,等效油耗降低了9.0%,HC排放量降低了2.7%,CO排放量降低了2.9%,NOx的排放量降低了7.8%.并且经过优化后的发动机工作点更多的分布在高效区间,同时能够使车辆在行驶过程中更加合理的分配发动机、电动机和ISG电机之间的转矩.