基于车辆制动后期的纵向振动控制

江治东,郑敏毅,张 农,2,夏祥军

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.合肥工业大学 汽车工程技术研究院,安徽 合肥 230009)

车辆平顺性是评价车辆性能的重要指标。平顺性研究主要集中在垂向动力学,如文献[1]通过调节刚度和阻尼,减少车身垂向振动的均方根值。自动驾驶领域的制动控制研究更多关注于冲击度和减速度,如文献[2]对纵向舒适性进行了调查和研究,指出车辆的减速度不大于0.15g和冲击度不大于0.2g/s。

文献[3]的试验结果表明,导致人不舒适的因素更多与频率、方向和振动持续时间相关。根据文献[4],振动的总均方根值是人体3个轴向均方根的加权,x、y这2个水平轴向的轴加权系数都比z轴加权系数要大,人体对纵向振动比横向振动更加敏感。因此研究纵向振动控制具有重要的意义。

文献[5]通过制动平顺性主观实验,将制动分为制动初期、制动中期和制动后期,结果表明制动强度越大,平顺性越差;在同一制动强度时,制动后期的平顺性更差。文献[6]研究了车辆制动停止时的轮胎特性,结果表明在制动过程中俯仰运动由悬架特性决定,而车辆的纵向抖动是由于轮胎的特性导致的。文献[7]进一步研究了低速时加速和减速轮胎特性的改变,设计两自由度控制策略,保证平顺加速和减速。文献[8]在进行主动避撞控制时考虑了驾驶员的驾驶习惯,通过模拟驾驶员的制动行为来提高避撞时的车辆平顺性。限制车辆减速度和冲击度不适合制动后期的振动抑制,这是由于没有考虑振动频率对舒适性的影响且没有考虑轮胎低速时的轮胎特性。

模型预测控制器(model predictive controller,MPC)基于预测模型对系统进行滚动优化,并实现反馈校正[9]。由于工业过程中多变量高维系统难以建立精确的数学模型,而且结构、参数以及环境具有不确定性、时变性、非线性等特点,最优控制难以实现,促进了MPC控制的发展。MPC是基于模型的控制,但对模型的要求不高;采用滚动优化策略,以局部优化取代全局最优;利用实测信息反馈校正,增强控制的鲁棒性。MPC控制与PID控制相比,不仅利用当前和过去的偏差值,还利用预测模型来预测过程未来的偏差值,以滚动优化确定当前的最优控制策略,使未来一段时间内被控变量与期望值偏差最小。

MPC广泛应用在车辆横、纵向控制中。由于本文模型具有线性时变的特点,使用MPC算法可使计算简单,实时性好。

针对制动后期的制动平顺性问题,本文首先试验分析车身和轮胎的纵向固有频率,再对制动后期减速度进行时域分析和频率分析,然后建立合适的轮胎模型,模拟试验工况,最后建立合适的控制算法,并进行试验验证。

1 纵向模态分析

1/4车辆纵向模型如图1所示。

图1 1/4车辆纵向模型

图1中，i=1,2,3,4;下标j表示f或r。

车身简化为刚体,质量为ms,纵向位移为zx,前、后4个簧下质量的纵向位移分别为zx1、zx2、zx3、zx4。五自由度车辆纵向模型参数见表1所列。

表1 车辆模型参数

车身质心的纵向运动方程为:

(1)

4个簧下质量的纵向运动方程分别如下:

kuf(qx1-zx1)

(2)

kuf(qx2-zx2)

(3)

kur(qx3-zx3)

(4)

kur(qx4-zx4)

(5)

其中,qx1、qx2、qx3、qx4为车轮的纵向位移。

以上5个微分方程代表了五自由度的车辆纵向动力学模型,采用矩阵形式可表示为:

(6)

对某SUV车进行纵向模态的识别试验,获取车辆簧上和簧下测点的纵向加速度信号,通过对加速度信号进行分析、处理,获取车辆纵向固有频率及对应的阻尼比、振型等模态参数。传感器分别安装在前、后轴簧下的左、右轮毂处和簧上横梁处,使用橡胶锤对车辆的左、右车轮沿纵向进行同向或反向的锤击试验。

车辆前轮同向锤击时右横梁的频率分析如图2所示。

图2 车辆前轮同向锤击时的横梁频率

根据(6)式进行多自由度复模态分析,系统的无阻尼固有频率、阻尼比和振型见表2所列。车辆纵向试验的簧下模态参数识别结果见表3所列。

由表2、表3和图2可知,不论从理论模态分析还是试验模态分析,车身的纵向固有频率在3.5 Hz左右,而轮胎纵向固有频率在20 Hz左右,甚至以上。

表2 系统纵向模态

表3 纵向试验模态参数识别结果

理论模态和试验模态的轮胎固有频率不同，这是由于理论车辆参数与选取的试验车辆参数不同导致的。

2 纵向制动建模

一般稳态轮胎模型(如魔术公式)可以很好地拟合轮胎试验数据,但是不能及时捕捉轮胎的动态特性。本文主要研究制动后期的纵向振动问题,需要考虑轮胎动态特性。文献[10]以刷子模型为基础,推导轮胎动力学摩擦模型,提出的LuGre动力学模型可以精确地描述轮胎摩擦力的瞬态特性,具有物理意义明确的优点。LuGre模型有集总式、分布式和平均集总式3种表达方式。其中平均集总式具有计算方便和反映分布式的特点,具体模型如下:

(7)

(8)

(9)

其中:σ0为纵向橡胶刚度;σ1为纵向橡胶阻尼;σ2为相对黏滞阻尼系数;vr为接触面的相对运动速度;zt为内部摩擦状态;g(vr)为正滑动函数;uc为归一化库伦摩擦力;us为归一化静态摩擦力；vs为Stribeck速度;α为Stribeck指数。

采用参考文献[11]中LuGre轮胎参数,可以得出在制动工况下不同速度的LuGre模型的稳态响应，如图3所示。

图3 LuGre模型不同速度下的稳态响应曲线

由于Lugre轮胎模型复杂,文献[5]提出了在低滑移率时使用刚度和阻尼系数表达纵向力和轮胎压缩量的关系,有效简化了LuGre模型对轮胎的瞬态响应特性的描述。动力挠度轮胎(dynamics deflection tire,DDT)模型表达式如下:

(10)

其中:Flong为轮胎受到的纵向力;轮胎压缩σx为轮胎中心位置相对于接触地面印记在纵向中心之间的距离。假设小压缩情况下,DDT线性化为:

(11)

其中：Dlong为轮胎纵向阻尼系数;Clong为轮胎纵向刚度系数。轮胎压缩σx可以表达为:

σx=xw-xcp,

其中:xw为车轮的位移;xcp为接触地面印记的相对位移。在DDT模型中,滑移率用轮胎压缩量定义,而不是用车轮速度定义。定义如下:

其中,σlong为轮胎松弛长度。因为轮胎上的输入转矩拉伸/压缩轮胎，所以接地印记的变化和轮胎有效半径的改变。接地印记相对速度可以表达如下:

其中:R0为轮胎自由滚动时有效半径;R0(1-λ)为轮胎的等效半径。

假设不考虑悬架对车辆纵向的影响,模型建立如下:

(12)

(13)

其中:M为整车质量;Iw为簧下的转动惯量;τ为制动力矩。状态方程表达式为:

(14)

本文仿真使用的参数为:Dlong=5 kN·s/m;Clong=400 kN/m;M=1 750 kg;Iw=3 kg/m2;R0=0.3 m;σlong=0.25 m。

车辆设定初始速度为18 m/s,以恒定制动力矩减速,速度变化曲线如图4所示,加速度变化曲线如图5所示。从图4可以看出,车辆在制动后期速度有波动;从图5可以看出,速度接近0时车辆的纵向即x向加速度发生振动,第1个峰值达到了减速度的60%。根据仿真频率,加速度可得峰值频率为3.052 Hz。

图4 仿真车辆速度

图5 仿真车辆加速度

如果考虑悬架对车身纵向振动的影响,那么使用下式建立车辆纵向动力学模型和车辆制动建模,的联系,即

σx=qxi-zxi

(15)

分别对不考虑悬架和考虑悬架的模型进行仿真。考虑悬架的车身加速度和不考虑悬架时整车加速度对比如图6所示。

图6 车身加速度和整车加速度的对比

由于考虑了车辆纵向的刚度和阻尼,车身加速度相对于整车加速度有延迟,但是由于车辆纵向刚度很大,车身加速度和整车加速度基本相同。因此在考虑制动后期的振动问题时,车辆悬架对其影响很小,可以忽略。

经分析,车辆在制动后期的振动频率减低至4 Hz以下,引起人体在制动后期的不舒适,同时车身的纵向固有频率在3～4 Hz之间,制动后期的振动频率有可能导致车身部件的共振,加剧人体的不舒适。因此,减低制动后期的振动非常重要,具有实用价值。

3 纵向制动建模

针对制动后期的振动问题,控制策略是在制动后期松开制动器。

一方面,使轮胎的振动不易传递至车身,使整车纵向振动响应频率增大,远离人体敏感区域;另一方面,由于制动器的松开,轮胎可继续运动,制动后期轮胎迟滞效应积累的能量可以通过旋转运动得到释放。

根据第2节,取状态变量、输入变量和输出变量如下:

U=τ,

Y=CX

(16)

其中

首先对方程进行离散化t=kT(k=1,2,…),则离散化后的方程为:

X(k+1)=A(k)X(k)+B(k)U(k),

Y(k)=C(k)X(k)

(17)

根据模型预测控制的基本原理,带约束的模型预测控制的优化问题可以描述为:

minzz=

umin≤uk≤umax,k=0,…,N-1;

ymin≤yk≤ymax,k=1,…,N;

Δumin≤Δuk≤Δumax,k=0,…,N-1

(18)

其中:Wy为跟踪误差的权重矩阵;WΔu为控制增量的权重矩阵,仿真时均设置为单位矩阵。

选取变量z为:

通过变换,(18)式变成二次型线性规划问题，即

[x(t)r(t)u(t-1)]FTz

(19)

(20)

4 仿真和实车验证

仿真工况设置初始速度为36 km/h,制动压力恒定为2 MPa。控制流程如图7所示,控制条件的触发有2种情况,理想情况是车速等于0时,另一种情况是车速比较小时,但未到0时。一般汽车的车速是由轮速传感器计算得来的,在低于1.8 km/h,车速检测不到,在车速小于2 km/h时介入MPC控制。

图7 控制流程

Simulink中搭建的MPC仿真模型主要由3个部分组成,分别为时变预测模型、MPC控制器和时变控制对象模型。时变预测模型主要根据时间的变化,输出预测步数的A、B、C、D等值;MPC控制器模型主要根据参考值计算下一步的输入；时变控制对象模型主要根据输入计算输出。评价纵向振动性能时,引用纵向加速度的加权均方根值来表征制动过程中的纵向平顺性。引用文献[8]中提出的四阶滤波函数来计算纵向加速度的均方根值,其表达式为:

Wd(s)=

(21)

仿真时不同触发条件下的加速度对比如图8所示。由图8可知,车辆在恒定压力下制动时,后期的振动冲击大,在车速等于0 km/h时介入控制,此时振动已经发生,但明显减少。

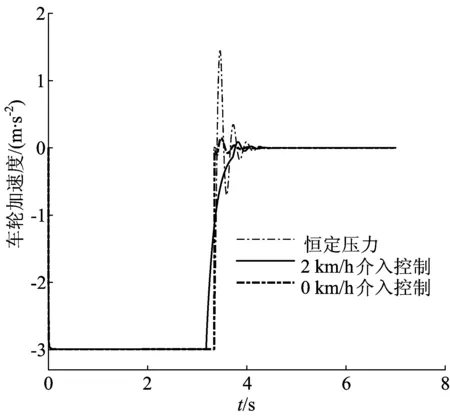
图8 不同触发条件下仿真加速度的对比

不同触发条件下的平顺性和制动距离的对比如图9所示。制动距离是评价制动安全性的重要指标。由图9可知,控制介入车速等于0时,制动距离不变;控制介入车速等于2 km/h时,制动距离增加了0.05 m;对非紧急工况制动时,增加的制动距离很小。但纵向加速度的均方根值,在控制介入车速等于0、2 km/h时,分别降低了9%、42%左右。权衡2种方案,车速低于2 km/h时控制介入,纵向振动平顺性大大提高。

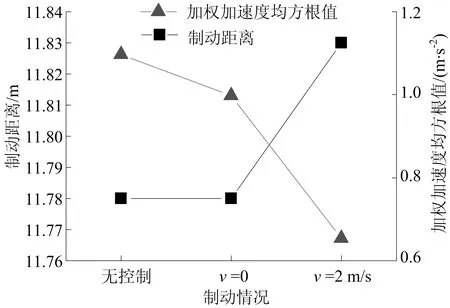
图9 不同触发条件下仿真平顺性和制动距离对比

本文验证原车在恒定压力下制动后期的振动现象和车速低于2 km/h介入控制策略下平顺性得到提高。试验车辆经过电子液压制动系统改装,采用惯导组合系统测量车辆的纵向加速度、车速等,采用dSPACE实习仿真系统完成控制算法部分。试验设备如图10所示。

图10 试验设备

试验车辆纵向加速度频率如图11所示。从图11可以看出,峰值频率为2.979 Hz。虽然实际车辆试验和仿真的结果不一致,但峰值频率在3 Hz左右的结论验证了前期分析和建模的准确性。

图11 试验车辆纵向加速度频率

试验车辆无控制和控制介入时纵向加速度的对比如图12所示。

从图12可以看出,在车速低于2 km/h时介入MPC控制,降低了纵向加速度的幅值,提高了乘坐的舒适性。

图12 试验车辆无控制和控制介入时纵向加速度的对比

5 结 论

本文对制动后期的纵向振动问题进行了研究。首先基于纵向动力学模型分析了整车的纵向固有频率并且试验验证,然后建立动态轮胎模型和制动模型,分析了制动后期纵向减速度的频率和时域响应,设计MPC控制器,提高纵向平顺性。仿真和试验结果得到如下结论:

(1) 制动后期的纵向振动峰值频率在3.0 Hz左右,在人体纵向敏感区域之间,车身纵向固有频率在3.3 Hz左右,制动后期的振动频率有可能导致车身部件的共振,加剧人体的不舒适性。

(2) 悬架由于纵向刚度很大,对制动后期的纵向振动影响很小,纵向振动主要由轮胎弹滞特性导致,减小制动后期的制动压力,可以使轮胎迟滞效应积累的能量通过旋转运动得到释放。

(3) 在车速低于2 km/h时,介入MPC控制,车辆纵向加权加速度的均方根值降低了42%,大大提高了制动后期的舒适性,制动距离比原车增加了5 cm,非紧急制动工况下可以接受。