基于卡诺图的QCA电路结构优化方法

朱仁俊,黄荣俊,2,宋志鑫,仇怀利,张永强

(1.合肥工业大学 电子科学与应用物理学院,安徽 合肥 230601; 2.成功大学 物理系,台湾 台南 701)

随着传统CMOS技术的快速发展,CMOS器件的特征尺寸在逐步减小。当设计规模进入深纳米级别时,晶体管中一些原本不存在的问题开始显现,如载流子效应、源漏间的隧道效应以及串扰等,这些问题不可避免且会对晶体管的工作效率产生巨大负面影响。因此,一些新兴的技术开始进入研究者的讨论视野。量子元胞自动机[1](quantum-dot cellular automata,QCA)便是其中之一。QCA提供了一种新的计算模型,模型的基础是量子效应以及电子间的库仑相互作用,在QCA电路中,信息的传递和转换是不依据电流而进行的。在行为表现方面,QCA具有功耗低、速度快、集成度高等特点。由于这些特点,许多学者对QCA进行了研究。

近年来,随着QCA的快速发展,电路的优化设计开始进入研究者的视野。文献[2-3]提出了一种新型的五输入择多门,并基于该择多门优化设计了全加器;文献[4-5]研究了RAM结构,思路是基于所提出的择多门进行优化设计;文献[6]提出了一种新型的异或门,并用该异或门针对性地设计了奇偶校验器,所设计出来的奇偶校验器在各方面性能均很优异;文献[7]基于特殊的择多门对D触发器结构进行优化设计,并将D触发器应用于存储器设计。目前,对电路优化方面的研究大多提出了新的结构,并基于该结构对某些电路进行优化,但没有一套较为完善的优化方法。

本文依据卡诺图化简方法提出了一套较为系统的电路优化方法,并利用该方法对最小项和形式的电路进行了优化设计。

1 QCA基础简介

在基于QCA的设计中,电路由QCA元胞组成。QCA元胞及传输线如图1所示,QCA元胞的形状为正方形,且1个QCA元胞包含4个固定量子点以及2个可自由移动的电子。

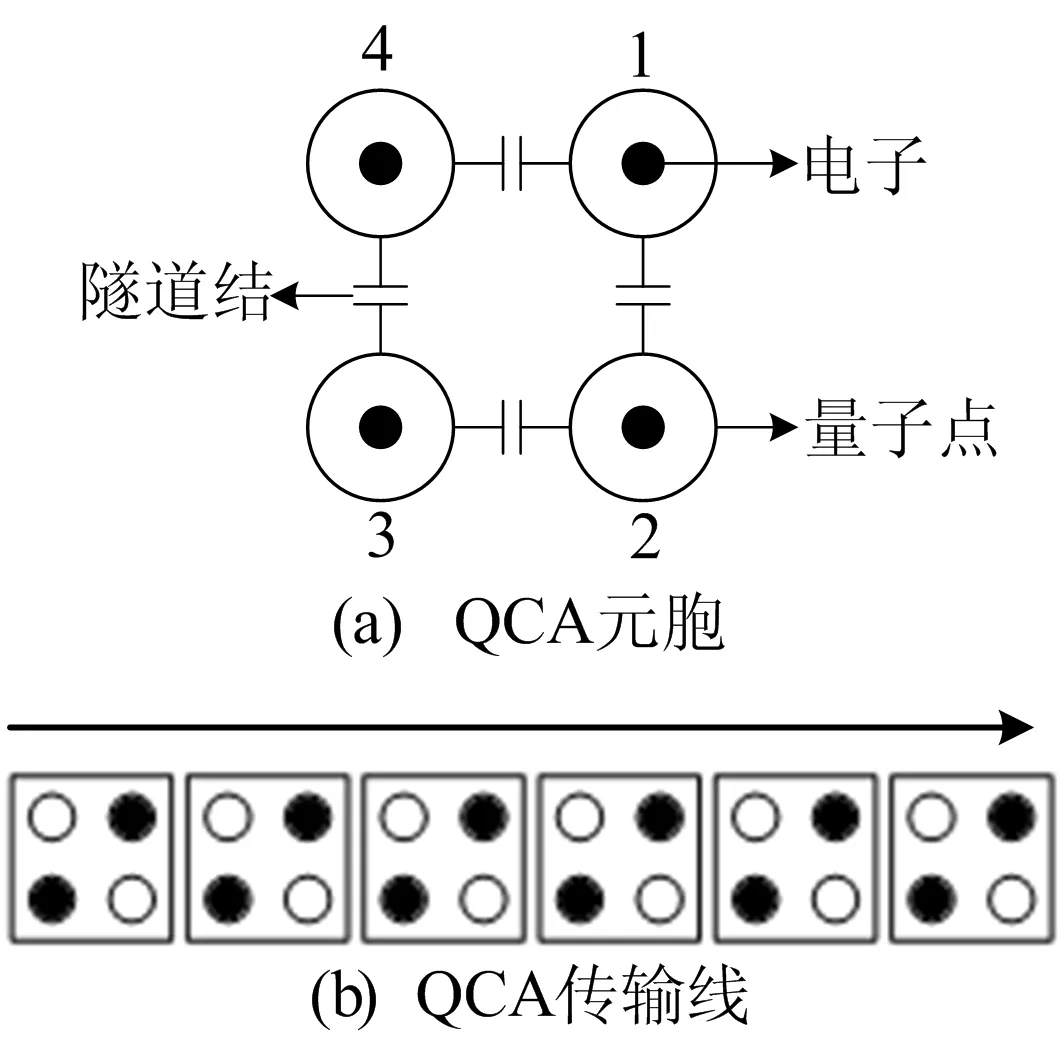
图1 QCA元胞及传输线

由于库伦排斥作用的存在,2个电子会出现在图1a所示的2个状态位置,这2种状态的极化值分别为“+1”和“-1”,将这2种状态分别对应二进制系统中逻辑“1”和“0”。在QCA电路中,信息的传输是以QCA传输线的方式进行的,根据能量最低原则,QCA传输线中相邻元胞的极化值趋于相同(图1b)。

QCA基本元器件为反相器和择多门,如图2所示。在QCA中,反相器逻辑功能为逻辑取反,其QCA版图如图2a所示。QCA择多门是QCA特色器件,如图2b所示,其逻辑功能表达式为F=M(A,B,C)=AB+AC+BC。电路中常用的“与或”逻辑可通过QCA择多门变种而来,如果将择多门一个输入的极化值置为“+1”(逻辑1),那么该择多门实现的逻辑功能为F=A+B,即为或门;如果将择多门一个输入的极化值置为“-1”(逻辑0),那么该择多门所实现的功能为F=AB,即为与门。

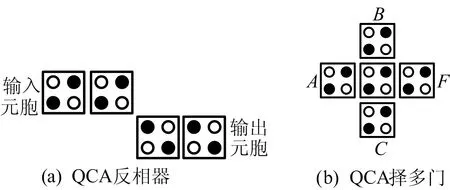
图2 QCA基本元器件

QCA电路时钟较为特殊,与经典电路中时钟的概念完全不同,如图3所示。

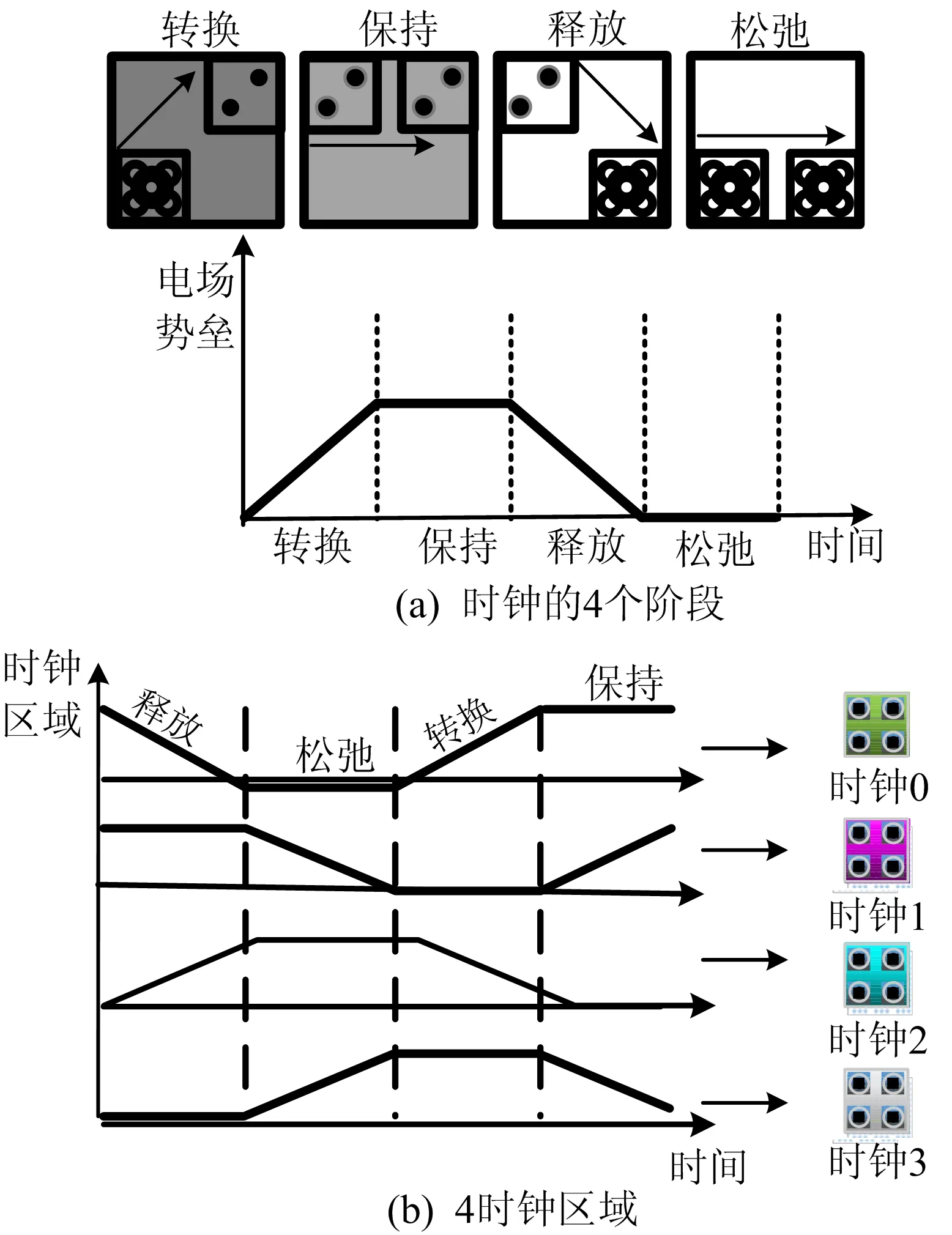
图3 QCA时钟

对于单个元胞来说,一个时钟周期分为4个阶段,分别为转换、保持、释放以及松驰阶段[8],如图3a所示。转换阶段,该元胞处于无极化状态并受其他元胞影响,因而极化值开始固定;保持阶段,该元胞极化状态稳定，不受任何影响;释放阶段,该元胞的极化状态开始由稳定变得不稳定;松驰阶段,该元胞的状态变为无极化状态。在单个元胞中,时钟的4个阶段依次变化,QCA中信息的存储是动态的。由于时钟的四相位行为,QCA电路中存在4个时钟区域,每个时钟区域元胞各自拥有完整的时钟周期,且相邻时钟区域的相位差为90°,如图3b所示。

2 基于类IP核的卡诺图优化方法

2.1 IP核与基于元胞间响应机理器件

在传统电路中,IP核(Intellectual Property core)是指经过反复验证过的、具有特定功能的宏模块。若一个IP核被广泛使用,则该IP核在某些方面参数相对优异。在QCA中,存在这样一类器件,这些器件并非基于“与或非”逻辑设计,而是依据QCA独特的工作机理实现的,该工作机理即为元胞间响应[9]。基于元胞间响应异或门如图4所示,该器件为文献[6]中所提出的基于元胞间响应机理的异或门,文献中对比了所提异或门与现有异或门的各方面性能,结果显示,与传统方法实现的器件相比,该器件在元胞数、面积、时延以及功耗等方面均表现得更为优秀。广义上,IP核是预先设计好的功能模块,基于元胞间响应器件也是具有特定功能的模块,因此将基于元胞间响应原理的器件定义为QCA中类IP核。

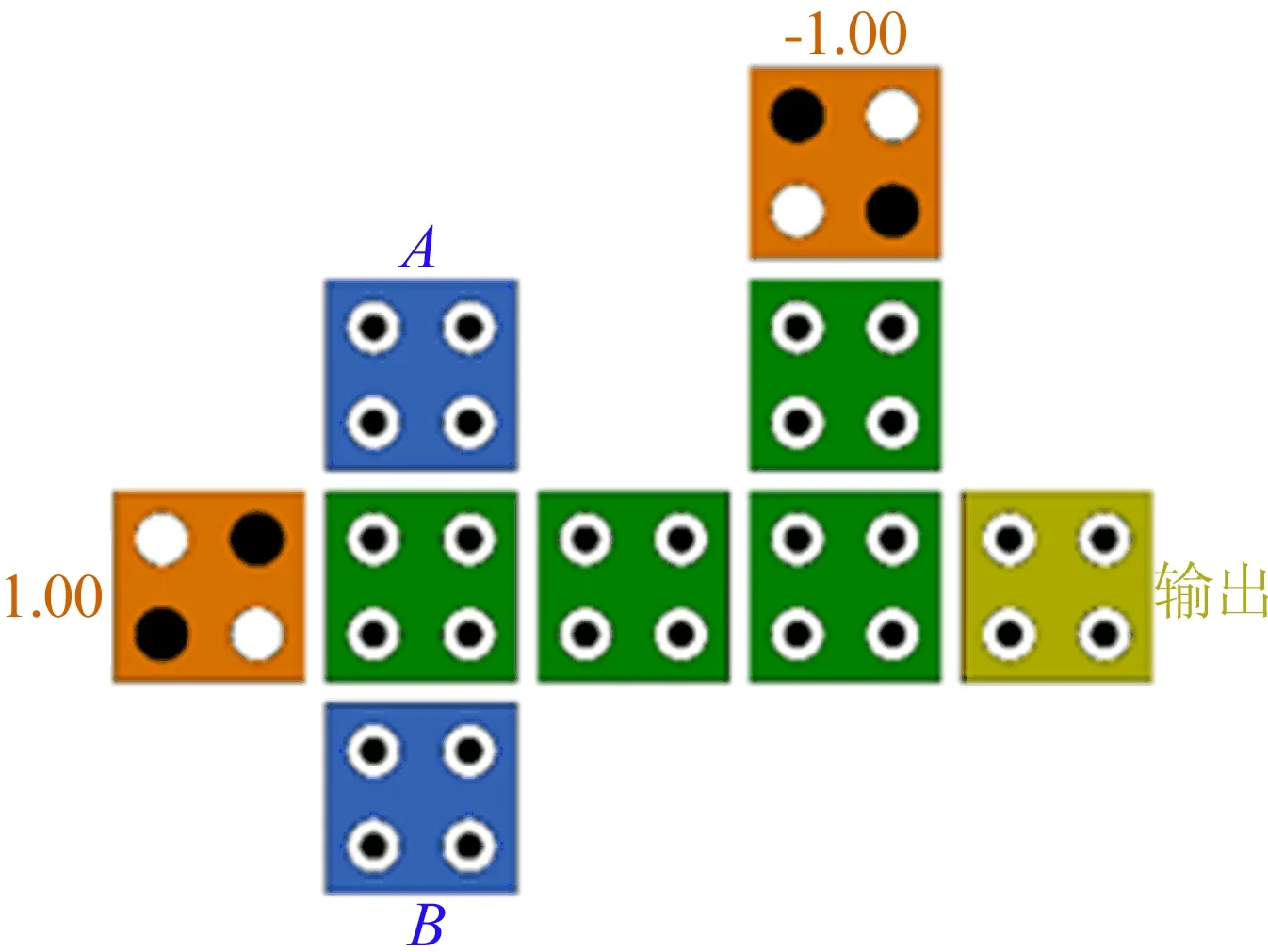
图4 基于元胞间响应异或门

2.2 基于类IP核的卡诺图

卡诺图是数字电路中较为常见的化简函数方法,在设计组合电路时,电路可以用卡诺图进行化简从而得到较优结果,卡诺图如图5所示。在QCA中,类IP核的提出本身就是为了简化结构,合理运用类IP核可以在一定程度上简化电路。这些类IP核在卡诺图上占据特定的位置,在基于卡诺图进行化简时,可以利用这些特定形状,运用类IP核来进行化简。例如,三输入择多门在卡诺图上占据的位置如图5a所示,异或门在卡诺图上的形状如图5b所示。

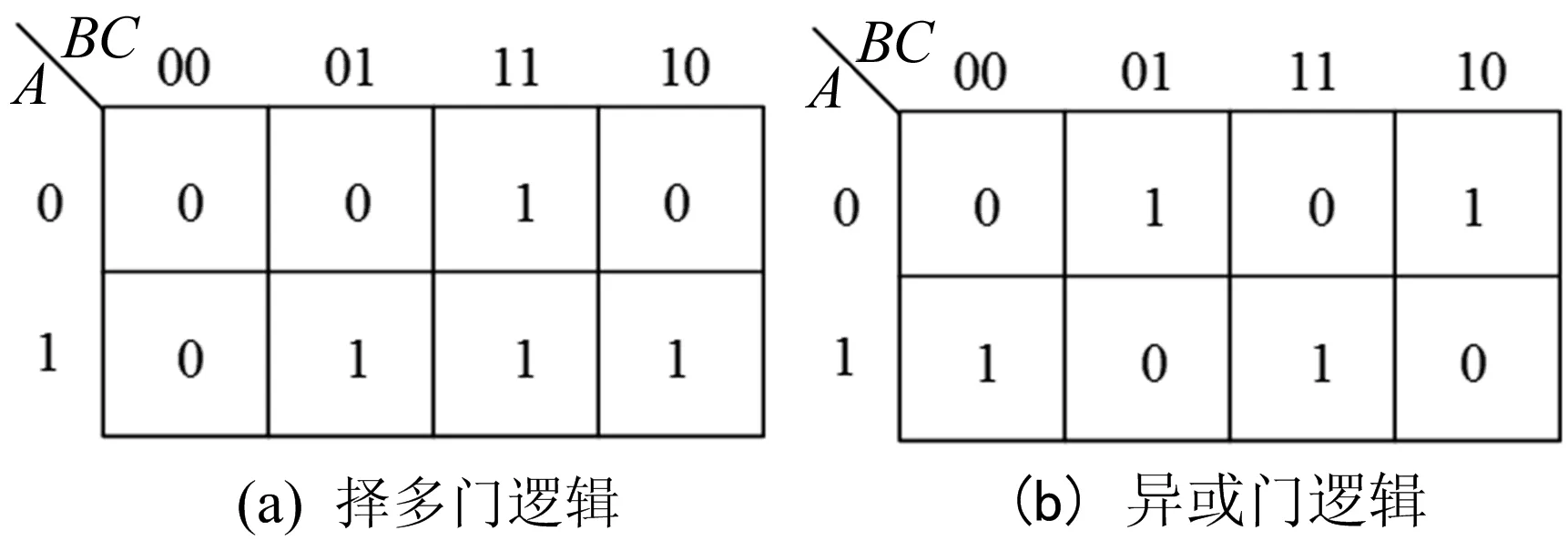
图5 卡诺图

2.3 优化方法

在传统数字电路设计中,对组合逻辑电路处理的方法是将其逻辑函数化至最简,但在QCA电路设计中由于交叉结构的冗余性,QCA版图的实现往往并不是最优的。为了简化电路结构和尽可能避免交叉结构，本文提出基于QCA类IP核卡诺图优化方法。基于QCA类IP核卡诺图优化方法具体步骤如下:

(1) 将目标电路用卡诺图表示。

(2) 比对类IP核卡诺图形状,若目标电路卡诺图中存在类IP核,则提取该部分,并将卡诺图的该部分置为无关项,转步骤(3);若不存在,转步骤(5)。

(3) 继续比对,直至不存在类IP核,并对剩余部分进行处理。

(4) 基于该逻辑QCA实现,比对各方面参数,若各参数均有提升或互斥参数相差小于5%，且优化参数提升超过15%,转步骤(9);若无提升,转步骤(5)。

(5) 将卡诺图逻辑取反。

(6) 比对类IP核卡诺图形状,若卡诺图中存在类IP核,则提取该部分,并将卡诺图的该部分置为无关项,转步骤(7);若不存在。

(7) 继续比对,直至不存在类IP核,并对剩余部分进行处理。

(8) 基于该逻辑QCA实现,并且结果取反,比对各方面参数,若各参数均有提升或互斥参数相差小于5%，且优化参数提升超过15%,转步骤(9);若无提升,转步骤(10)。

(9) 电路优化完成。

(10) 电路无法优化,原电路为最优电路。

3 应用及分析

3.1 异或/同或类IP核

异或/同或逻辑在卡诺图化简上扮演着重要角色(图5b),在该卡诺图上,只要不在相邻位置,就存在异或或者同或关系,扩展到多阶卡诺图上,可以发现该现象同样存在。在卡诺图上,相邻位置的最小项可以化简合并消去一个输入变量,而异或/同或逻辑这一特性意味着非相邻位置也可以合并以消除一个输入变量,从而简化逻辑。在QCA相关研究中,对异或门的研究颇多,文献[6,10-11]中异或门均以元胞间响应工作原理设计,其中,文献[6]中所提出的异或门结构在各方面性能目前为最优(图4),因此选取该异或门作为本文异或类IP核。同或逻辑可以通过异或逻辑取反,因而同或类IP核不需要专门研究。

3.2 组合逻辑电路结构优化

组合逻辑电路的函数形式均可用最小项和来表示,而2个最小项和形式的电路是组合电路中最为基础的电路,任何其他形式的电路都在该电路的基础上构建而成。二输入变量电路因为输入变量太少没有可分析性,因此从三输入变量电路开始分析。

在众多三输入变量电路中,逻辑表达式F=ABC+A′B′C′在电路实现时最为复杂,函数F=ABC+A′B′C′逻辑图及QCA版图如图6所示。

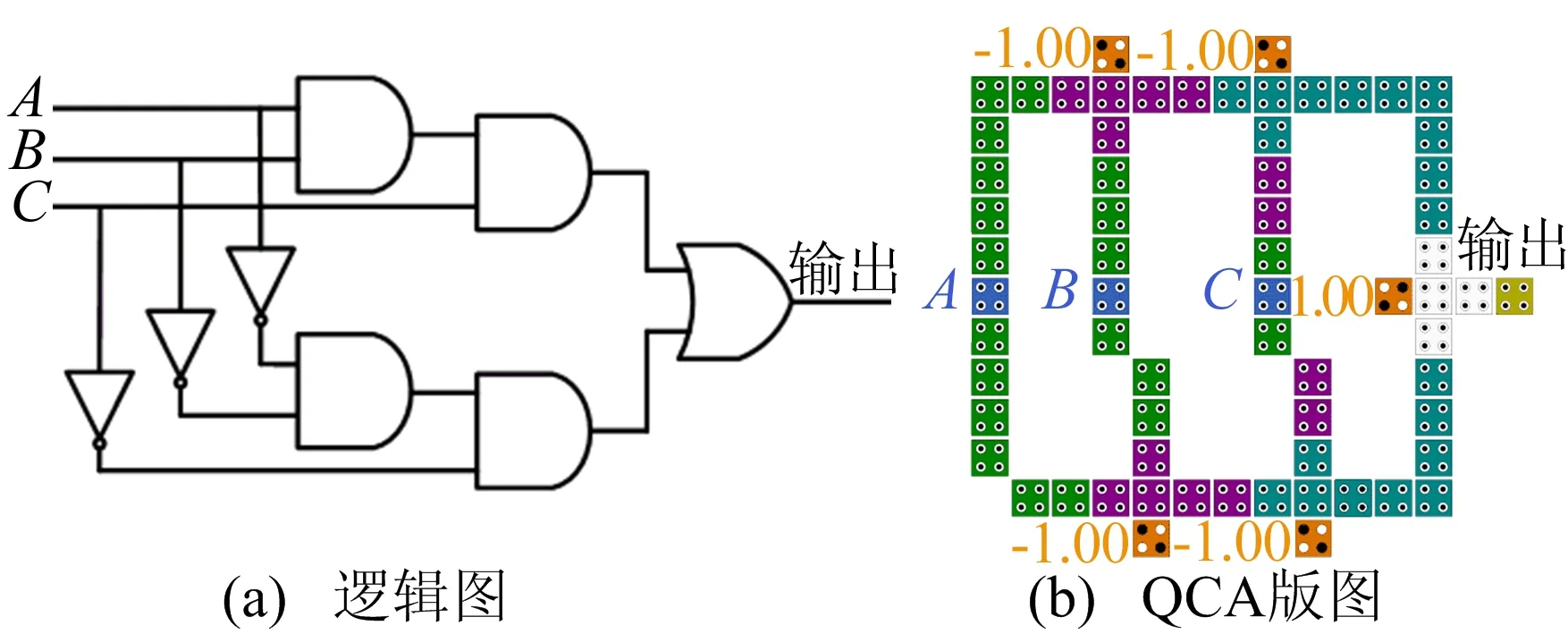
图6 函数F=ABC+A′B′C′逻辑图及QCA版图

虽然该QCA版图中不存在交叉线,但电路的输入接口在内部,引线时将会带来交叉线。基于QCA类IP核卡诺图优化方法对该电路进行优化设计,卡诺图优化过程如图7所示,函数F=ABC+A′B′C′优化后逻辑图及QCA版图如图8所示。对比图6a、图8a可以发现,优化后电路结构明显更简单。

图7 基于类IP核卡诺图优化过程

图8 函数F=ABC+A′B′C′优化后逻辑图及QCA版图

在四输入变量中,同样以最复杂的逻辑函数F=ABCD+A′B′C′D′为例,基于QCA类IP核卡诺图方法优化后逻辑图及QCA版图如图9所示。对于n变量输入的2个最小项和形式的电路,所提方法仍然适用且优化后的逻辑有规律可循。n变量输入电路经优化后其逻辑电路图及QCA版图如图10所示,每增加1位输入,优化后逻辑图增加1个异或门以及1个同或门。对于更多数量最小项和形式电路,经实验发现所提优化方法同样可以起到优化电路的作用。

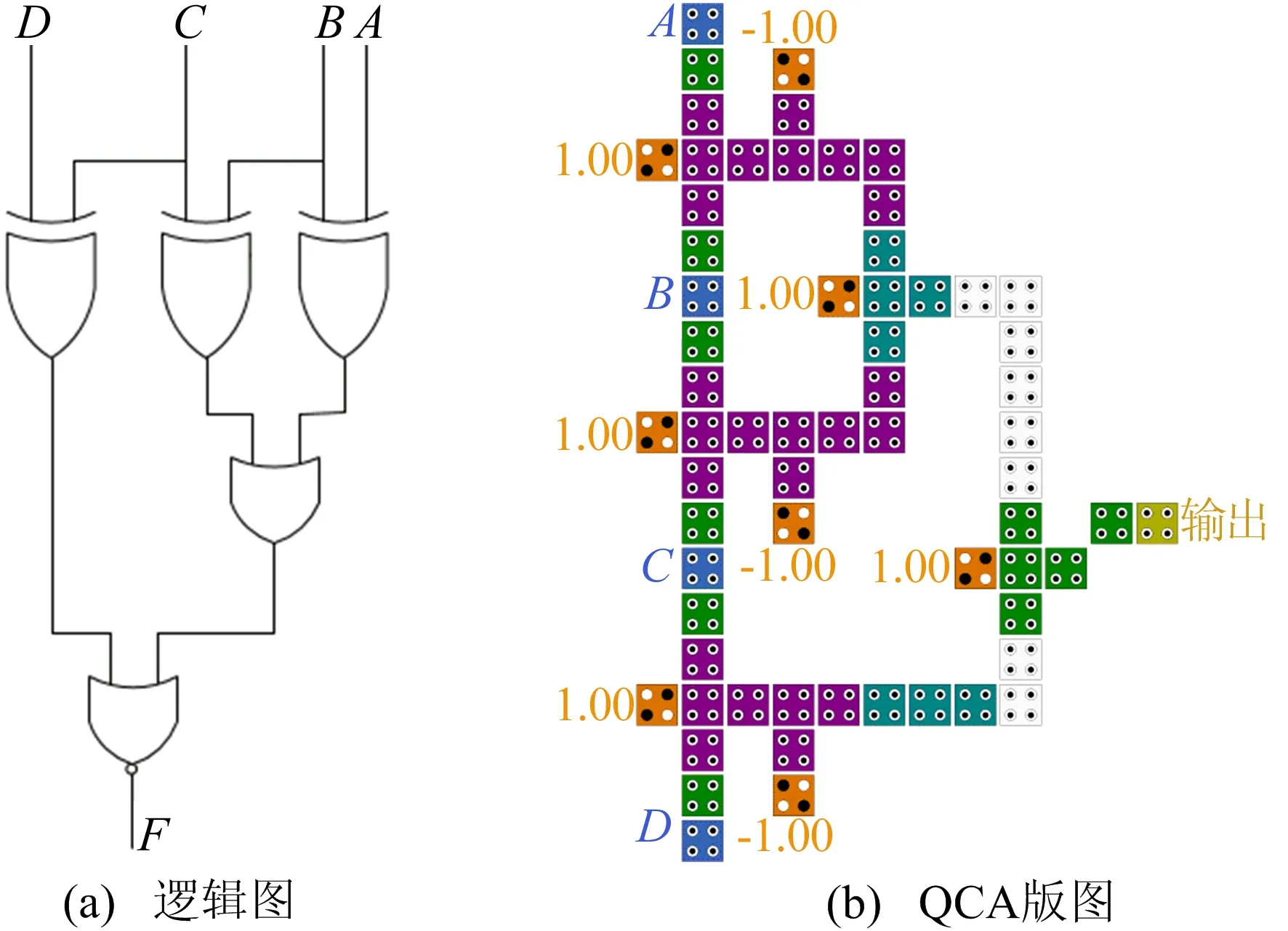
图9 函数F=ABCD+A′B′C′D′优化后逻辑图及QCA版图

图10 优化后n变量最小项两项和电路逻辑图及QCA版图

上述基于类IP核卡诺图优化方法所采用的类IP核为异或类IP核,其他基于QCA元胞间响应的类IP核,如择多逻辑、数据选择逻辑等类IP核,在合适情况同样可以使用。

以QCA特色元器件择多门为例,该器件本身就是基于元胞间响应原理构成的,逻辑表达式为F=AB′C′+A′BC′的电路,经择多门类IP核卡诺图优化方法优化后得逻辑表达式F=(M(A,B,C)+A′B′)′,优化后电路仅由3个择多门以及3个反相器构成。

4 仿真结果与比较分析

为了证明所提方法优化后QCA电路的正确性,本文采用QCADesigner[12]仿真软件来验证。优化后三输入变量、四输入变量两最小项和电路仿真结果如图11所示。

从图11a可以看出,一个循环内,开始和结束输出为1,其余时刻输出为0,这也符合逻辑表达式F=ABC+A′B′C的真值结果。图11b中最开始输出为0而非1,是因为图9b电路存在1个时钟周期的延迟,因此第1时钟周期输出结果不予考虑。

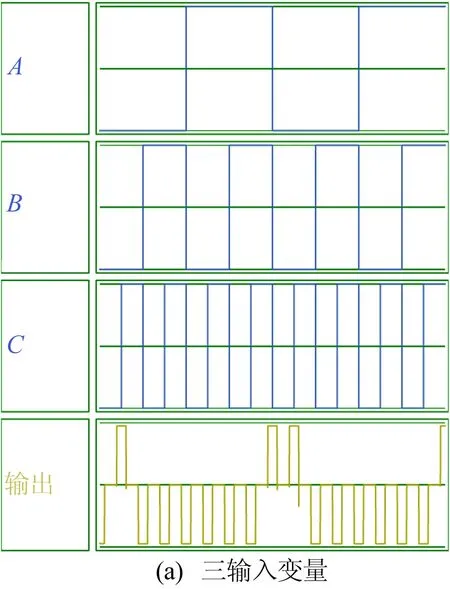
图11 优化后最小项两项和电路仿真结果

优化后电路的各项参数与原电路的比较结果见表1所列。

表1 优化后电路的各项参数与原电路的比较结果

基于类IP核卡诺图优化方法获得的电路在各性能指标上均优于原电路,随着输入变量位数的增加,基础复杂门(指的是择多门、异或门等)、面积以及时延方面差值变化不大,而反相器和元胞数差值则越来越大。时延方面是因为规模较小的电路不需要考虑时钟线长度时,基础复杂门增长一致且延迟相同;面积是因为优化前后元胞在水平和垂直方向增长幅度相差不大,以及QCADesigner独特计算方式和误差所决定的。原电路和优化后电路元胞数增长曲线及差值曲线如图12所示。

从图12可以看出,在元胞数方面,随着位数的增加,优化效果也越来越明显。

图12 原电路和优化后电路元胞数增长曲线及差值曲线

5 结 论

本文提出一种基于QCA类IP核卡诺图优化电路结构的方法并进行了初步验证。基于异或类IP核优化后的电路不仅在各参数上表现优越,同时该结构可扩展且没有交叉线,因而该类电路可作为基本模块电路被更为复杂的电路调用。本文主要运用了异或类IP核,数据结果表明,应用本文所提的优化方法对电路进行优化具有可行性。在QCA中还存在其他类IP核,如择多逻辑、数据选择等,在合适情况下这些类IP核可以极大优化电路结构。本文的不足之处在于实验样本量太少,无法证明在其他电路的适用性。