一种适应度排序的高维多目标粒子群优化算法

杨五四，陈 莉，王 毅，张茂省

(1.西北大学 信息科学与技术学院，陕西 西安 710021；2.中国地质调查局西安地质调查中心 自然资源部黄土地质灾害重点实验室，陕西 西安 710054)

多目标优化问题是一类复杂的最优化问题。常规多目标优化算法虽能够有效解决2或3个目标的多目标优化问题，但求解高维多目标优化问题(n≥4)的效果并不理想。其主要原因有：随着问题目标维数的增加，采用常规帕累托(Pareto)支配关系将有可能导致算法对非支配解的选择压力不足，使得非支配解难以有效逼近真实帕累托前沿；另外，由于高维多目标优化问题的帕累托最优前沿为超曲面，导致帕累托最优解集及对应可行解搜索空间的规模呈指数级增长，从而使算法收敛速度大幅下降。如何有效求解高维多目标优化问题，研究更优的高维多目标优化方法是目前进化多目标优化领域所面临的难题之一。现有的方法，如在搜索过程中结合偏好信息以缩小帕累托前沿区域[1-2]，通过宽松的帕累托支配关系来增强算法选择压力，如格支配[3]、K支配[4]、直觉模糊支配[5]、α支配[6]、模糊支配[7]等，以及采用新的比较准则对个体收敛性能的优劣进行比较与排序，以实现非支配个体之间的性能比较[8-9]。

针对高维多目标优化问题，考虑到集成适应度排序[8]是一种非帕累托支配排序方式，文中提出了一种集成适应度排序的高维多目标粒子群优化算法。即通过获取种群中个体与参考点最近的确定维度向量，其中向量维度参数设为K，首先使用基于惩罚的边界交叉方法(PBI)作为适应度函数来对种群中的个体进行排序，然后对较差的个体进行剔除，并将精英个体保存到外部档案中；同时，虽然粒子优化算法[10]具有较强的局部和全局搜索功能，以及收敛速度较快、算法参数较少等优良特性，但其易落入局部最优，影响算法效果，因而采用双搜索策略的粒子群优化算法[11]对种群进行寻优搜索。

1 集成适应度排序

集成适应度排序方法在文献[8]中是这样描述的：对种群P每个个体与预先定义的均匀分布参考点W进行关联，据此求出每个个体的最近权向量L，并选出前K个(其中K远远小于N)权向量，其中K为提前定义的常数。将已选权向量与N个适应度函数相关联，这里采用基于惩罚的边界交叉函数作为适应度函数，具体数学形式如式(1)所示。每个适应度函数对部分个体进行非递减排序，并根据个体的优劣进行编号，得到每个个体排序向量R。与文献[8]不同之处在于没有直接计算出每个个体最大排序序号，而是通过向量R结合参考点W对种群进行选择，并将精英个体保存在档案中，同时，采用算法NSGA-Ⅲ[12]的归一化方法对种群进行处理，集成适应度排序的算法流程见算法1。

算法1集成适应度排序(Ensemble Fit Ranking)。

输入：种群P，参考点W，控制参数K。

输出：每个解的全局排序序数RankNumber。

① [N，M]←size(P)

②NW←size(W)

③P←Normalization(P)

④rank←AssociationSort(P，W)

⑤L←GetClosestWeightVectors(K)

⑥Distance←GetPBIValue(L，K)

⑦r←GetSortNumber(Distance)

⑧Distance←Distance(Distance≠inf)=1

⑨RankNumber←r*Distance

基于惩罚的边界交叉方法[13]的数学形式如下：

mingpbi(x|λi，z*)=d1+θd2，

(1)

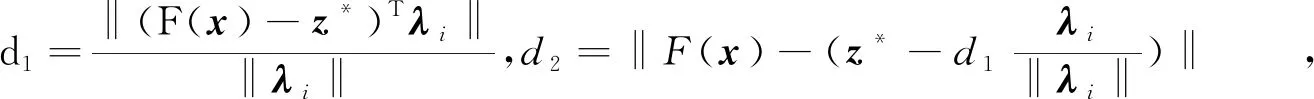
z*为理想点，θ为罚参数，λi为权重向量，x为决策向量。

2 基于集成适应度排序的高维多目标粒子群优化算法MaPSO-EFR

2.1 算法描述

基于帕累托支配的高维多目标优化算法在求解高维多目标优化问题时具有一定的局限性，而基于非帕累托支配的排序方法的主要优势在于放弃了帕累托支配方法中较为严格的个体优劣衡量标准，通过新的比较准则对个体收敛性能的优劣进行比较与排序，以实现非支配个体之间的性能比较，可有效提升对精英个体的选择压力，提高了算法的收敛精度，而且使得算法选择压力的提升不受目标维数增加的影响，从根本上解决了目标维数增多时精英个体选择压力退化的问题。基于此，提出一种集成适应度排序的高维多目标粒子群优化算法(MaPSO-EFR)，其算法流程如算法2和算法3所示。

算法2高维多目标粒子群优化算法(MaPSO-EFR)。

输入：种群大小N，控制参数K，最大迭代次数Gmax。

输出：种群P。

① 初始种群P，产生一组均匀分布的参考点W

②Archive←UpdateArchive(P，W，N，K)

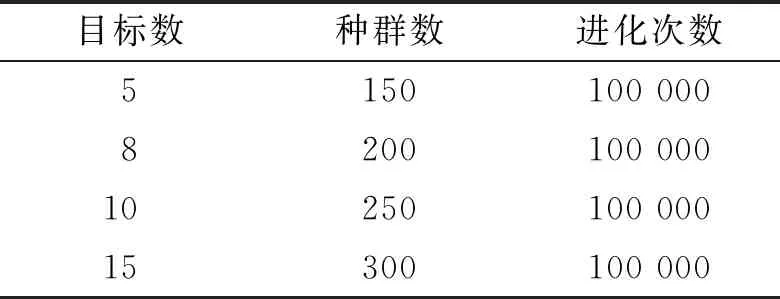
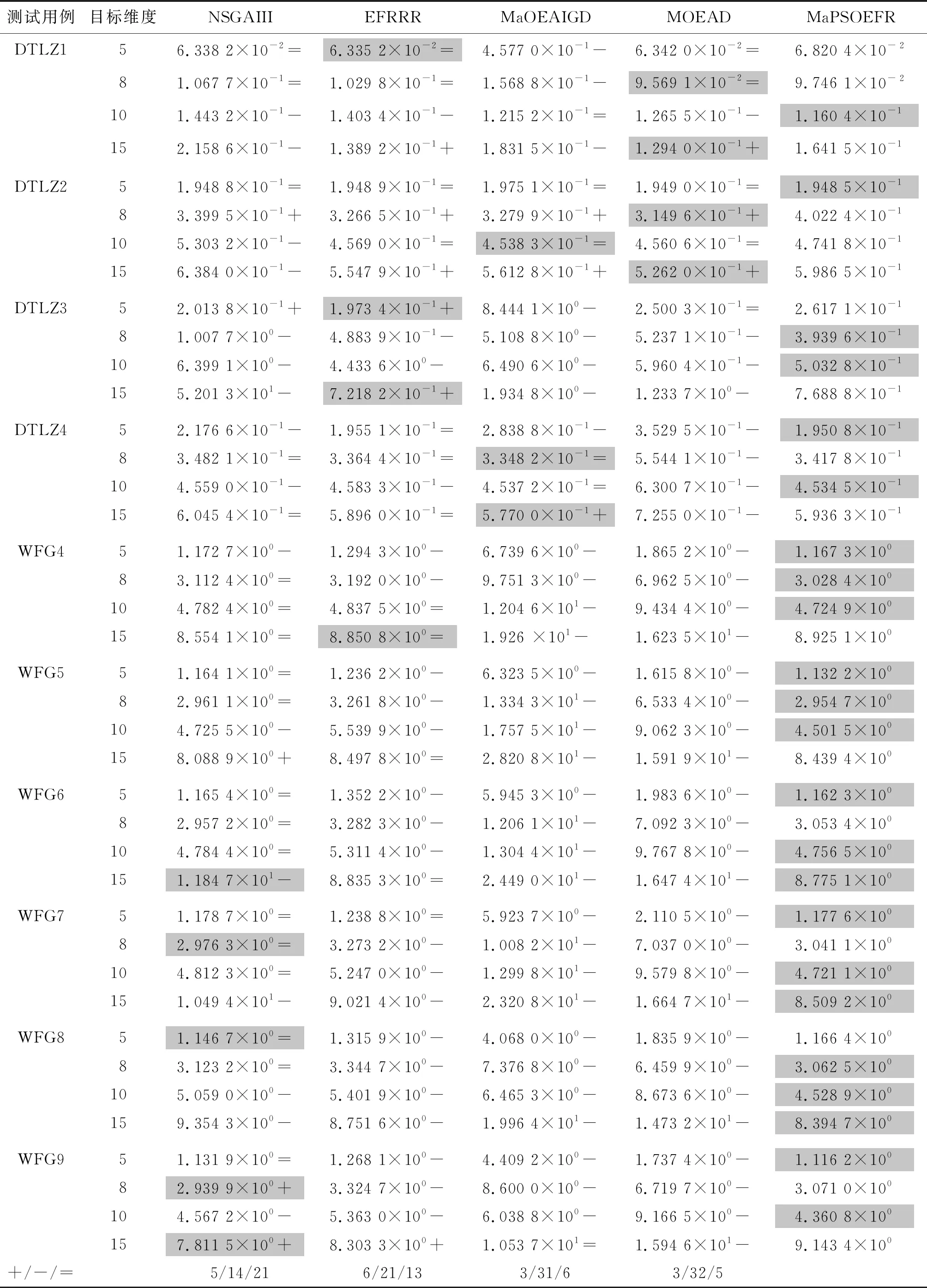
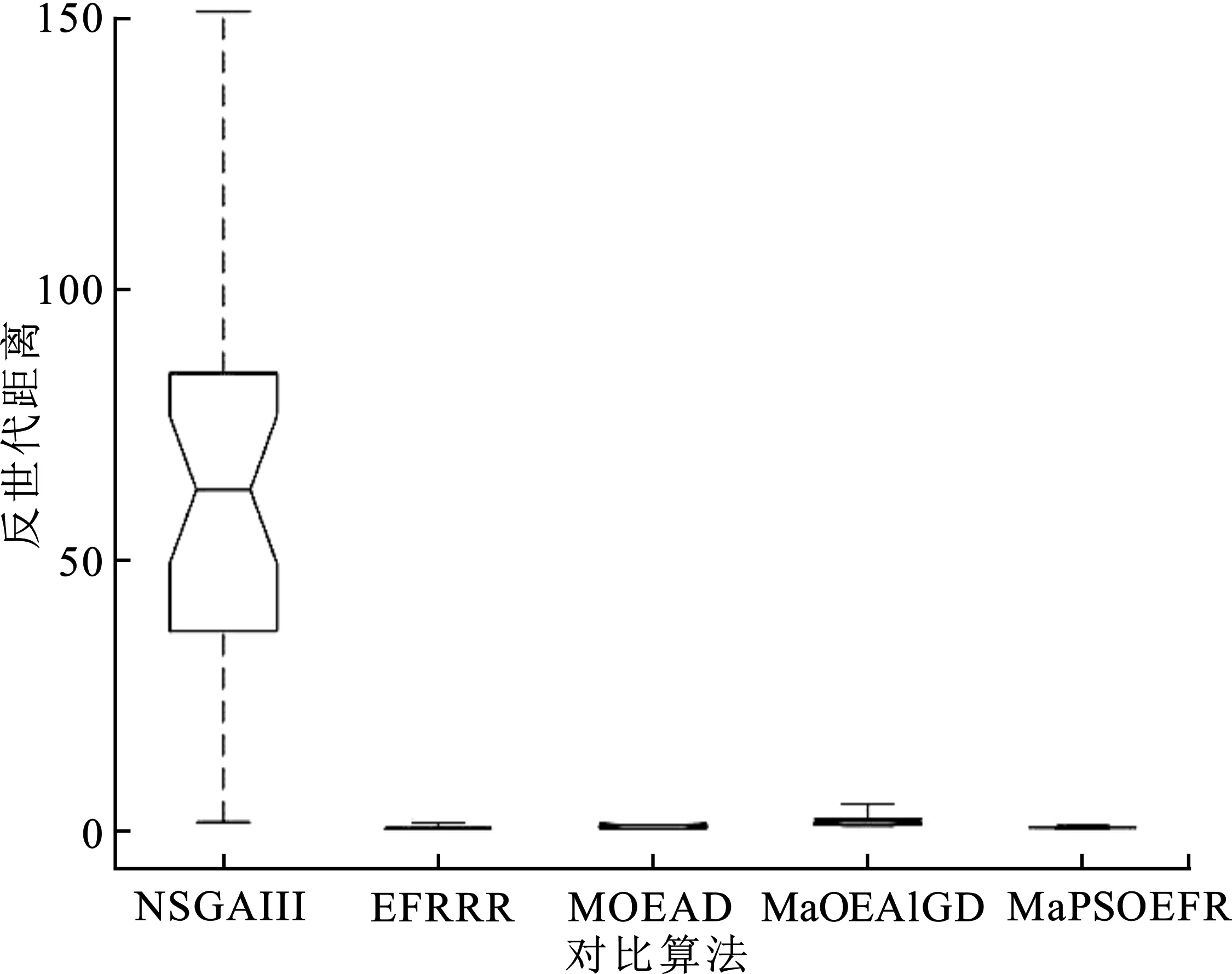
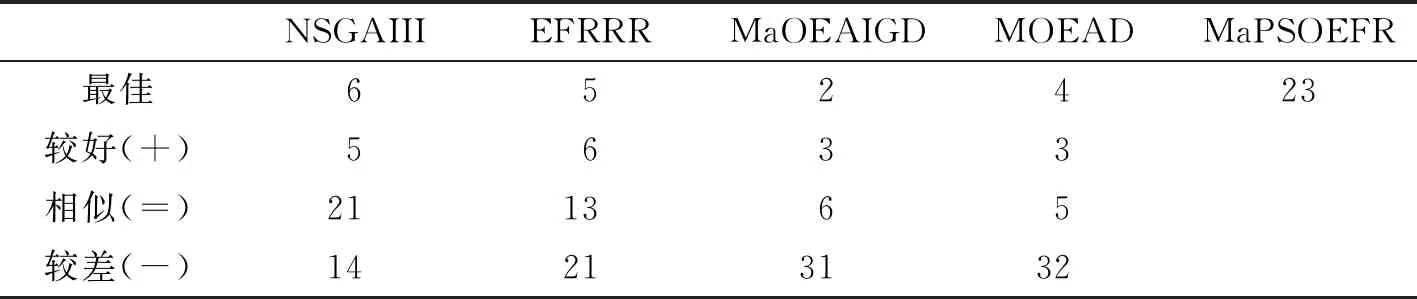
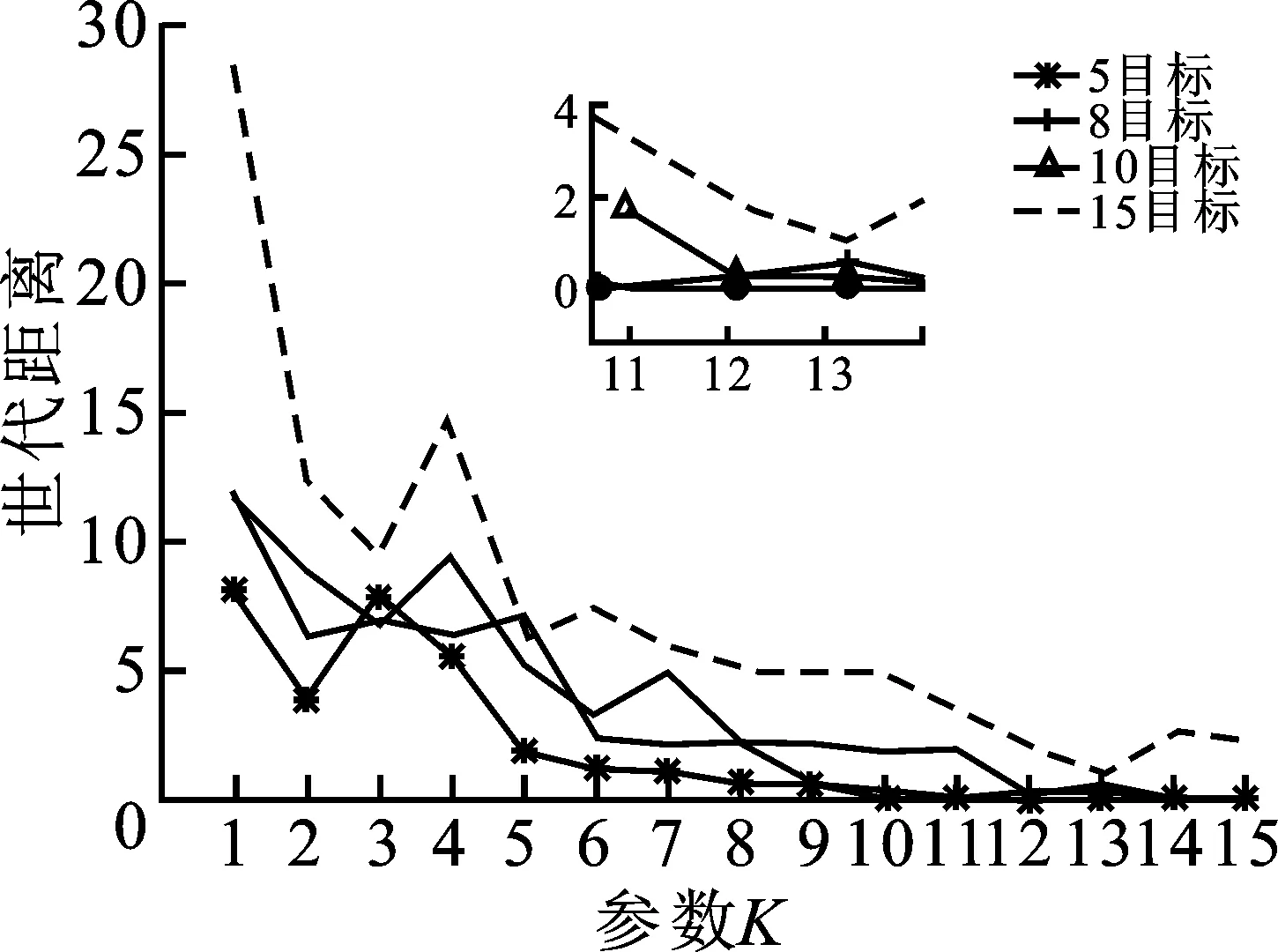
③ whileG

④P←Operator(P，Archive)

⑤Archive←UpdateArchive([P，Archive]，W，N，K)

⑥Offspring←DE_Operator(Archive)

⑦Archive←UpdateArchive([Offspring，Archive]，W，N，K)

⑧ end while

算法3外部档案更新(UpdateArchive)。

输入：种群P，参考点W，种群大小N，控制参数K。

输出：更新后种群Archive。

①RankNumber←EnsembleFitRanking(P，W，K)

②RP←1：length(P)

③RR←1：length(W)

④ While length(RP)>length(P)-N

⑤ [temp，imin]=min(RankNumber(RP，RR))

⑥RP←Delete disadvantaged individuals(temp，imin)

⑦ end while

⑦Archive←P(RP)

算法MaPSO-EFR的总流程：首先初始化种群P，并在目标空间中产生一组均匀分布的参考点W，并初始化外部档案，在while循环中，使用双搜索策略的粒子群优化算法对种群P进行更新，得到新种群P，然后更新档案，利用差分进化算子对档案中的个体进行交叉、变异等操作，得到子群，最后再次更新档案，直到循环迭代满足结束条件。外部档案更新流程如算法3所示，首先通过集成适应度排序获取各向量排序后的序号，计算出当前种群的大小，以及参考点数量，进入while循环中，通过种群与参考点的关系对最小的序号进行选择，删除较差的个体，直到满足循环终止条件，最后将精英个体保存在外部档案中。

2.2 计算复杂度分析

算法MaPSO-EFR的计算时间复杂度主要在于排序，其中归一化操作的时间复杂度为O(m2N)，而全局排序序号的计算的时间复杂度为max{O(mN2)，O(N2logN)}，综合考虑算法MaPSO-EFR的计算复杂度为max {O(mN2)，O(N2logN)}。

3 实验结果与分析

仿真实验在Intel Core i7-6500u 、8 GB内存、2.50 GHz 主频的双核CPU与Windows 1064位操作系统的个人电脑上运行。为了测试算法MaPSO-EFR的性能，选取性能先进的4种高维多目标进化优化算法进行对比，分别为EFRRR[8]、NSGA-III[12]、MOEA/D[14]、MaOEAIGD[15]，所有算法在多目标进化算法开源平台PlatEMO[16]上进行对比验证。

3.1 测试函数与评价指标

选取标准测试问题DTLZ1-4和WFG的部分测试实例，分别在5，8，10，15目标上进行仿真实验。测试问题决策变量的设置如表1所示。其中，m为目标数，n为决策变量数，k为位置变量，l为距离变量。采用综合性能指标反世代距离(IGD)对算法性能进行评价。

表1 测试问题的决策变量设置

3.2 实验参数设置

表2 目标数、种群数与进化次数设置

每个算法在测试用例上分别独立运行30次，并取均值作为最终结果；所有对比算法的参数设置均采用原文献中的数值，变异算子采用多项式变异，其中ηm=20，pm=1/n；集成适应度排序参数K设置为目标数，根据目标数的增加而变化。测试实例的目标数，采用的种群数以及算法进化次数如表2所示。

3.3 实验结果与分析

为了更客观地评估实验结果，采用Wilcoxon秩和检验对所有对比算法进行两两比较，显著性水平设为0.05，其中“+”、“-”和“=”分别表示对比算法性能优于、劣于和相似于提出的算法，其中最优值用灰色背景进行标注。

表3 统计了5种对比算法的最终实验结果。从表中可以直观地看到，算法MaPSO-EFR在大部分测试问题上的表现优于其他对比算法。其中，在测试问题DTLZ上，以略微的优势领先于其它算法，而在测试问题WFG上，算法MaPSO-EFR的性能表现明显优于其它算法，比同样采用集成适应度排序的EFRRR获得的最佳测试实例的数量多一些。但是算法MaPSO-EFR的集成适应度的方式与算法EFRRR还是有很大的不同，前者采用基于惩罚的边界交叉方法作为适应度函数，而后者使用切比雪夫函数作为适应度函数；基于惩罚的边界交叉方法分为两部分，一部分强调收敛性，另一部分强调多样性，使得其在某些测试用例上的表现优于切比雪夫方法。但这不是说基于惩罚的边界交叉方法在所有问题上都优于切比雪夫方法。另外，算法MaPSO-EFR没有采用EFRRR中的最大排序模式选择个体，而是通过参考点对标记序号的个体进一步选择，并保存最优个体进入下一代，这样可以避免在某一方向上重复选择个体，在保证种群收敛性的同时，保证种群的多样性。

表4对表3中各对比算法在测试实例上所获得Wilcoxon秩和检验的最佳、较好(+)、相似(=)、较差(-)等进行了统计。其中，算法MaPSO-EFR获得了23个最佳性能表现的测试实例，占总数的57.5%；算法NSGA-III在6个测试实例上的性能最优，而且在21个测试实例上的性能与算法MaPSO-EFR的相似，在4个对比算法中性能综合表现最好。

为了更直观地评价算法MaPSO-EFR性能表现，以5种对比算法在实例DTLZ3的15目标上的测试为例，采用折线图、盒图等可视化工具进行说明。其中，图1(a)描绘出了各对比算法的反世代距离指标随着迭代次数的增加而变化的折线，可以明显地看出对比算法NSGA-III，MaOEA-IGD的收敛性不如算法MaPSO-EFR和EFRRR；算法MaPSO-EFR收敛性表现几乎和算法EFRRR是一样的，但还是稍逊于算法EFRRR。虽然MOEA/D的收敛性表现比算法MaPSO-EFR和EFRRR都要好，但从表3中的数据容易发现，算法MOEA/D在DTLZ3的15目标上表现不稳定。图1(b)将各对比算法在DTLZ3的15目标上的30次实验数据用盒图的方式进行了说明。直观上可以看出，算法NSGA-III的表现最差，算法EFRRR和算法MaPSO-EFR的性能表现相似。

表3 算法MaPSO-EFR与四种对比算法在DTLZ和WFG的不同目标维数上获得的IGD平均值和标准差

(a) 5种对比算法的收敛性能曲线对比

(b) 5种对比算法收敛性能的盒图对比

表4 所有对比算法实验结果总结

综上分析，算法MaPSO-EFR在采用的大多数测试问题上获得了比对比算法更好的表现，表明提出的算法具有较好的收敛性和多样性，具有一定的竞争性。

3.4 参数K的讨论

参数K是一个平衡算法收敛性与多样性的控制参数。为了讨论其对算法评价结果的影响，除了上述反世代距离指标，另外还采用世代距离指标(GD)、空间评价指标(SP)这两个指标。其中，世代距离指标用于评价算法的收敛性能，所得解集的世代距离评价指标值越小越好；空间评价指标用于反映算法所得解集分布的均匀性，空间评价指标值越小，解集的分布越均匀。在测试实例DTLZ3的5，8，10，15目标上，分别取[1，15]之间的整数来对参数K进行实验，对于每个K值，算法程序运行30次并取平均值。最终结果如图2所示。

(a) 参数K对世代距离指标的影响

(b) 参数K对空间评价指标的影响

(c) 参数K对指标反世代距离的影响

从图2(a)和(b)可以看出，算法MaPSO-EFR在DTLZ3的不同目标数上的世代距离和空间评价指标随着参数K的增加呈下降趋势，说明参数K的取值对算法的收敛性和多样性有较大影响。而在图2(c)中，参数K在取值3以后，反世代距离指标变化幅度趋于稳定，也就是说，参数K对综合指标反世代距离的影响比较小。从而说明了针对不同目标维数，需要设定不同的K值，才可以使得算法性能表现更佳。

4 结束语

针对高维多目标优化问题，考虑集成适应度排序是一种非帕累托支配排序方式，提出了一种集成适应度排序的高维多目标粒子群优化算法。首先，对种群P每个个体与预先定义的均匀分布参考点W进行关联，求出每个个体的最近权向量L，并选出前K个权向量，采用基于惩罚的边界交叉方法作为适应度函数，对部分个体进行非递减排序，并根据个体的优劣进行排序编号。然后，对较差的个体进行剔除，并保存精英个体到外部档案中进入下一次迭代更新。最后，讨论了参数K值对算法性能的影响。与4种先进的高维多目标进化优化算法在标准测试集DTLZ和WFG的实验表明，算法MaPSO-EFR在大多数测试实例上的性能表现优于对比算法，具有较好的收敛性与多样性。但是算法MaPSO-EFR在一些退化的多目标测试问题上表现不理想，接下来工作将继续改善算法MaPSO-EFR的性能。