顺北一区小井眼超深井井筒温度场特征研究与应用

苏 雄， 杨明合， 陈伟峰， 张 俊

（1.中国石油钻井工程重点实验室长江大学研究室，湖北武汉 434000；2.中国石油集团工程技术研究院有限公司，北京 102206；3.中国石化西北油田分公司石油工程技术研究院，新疆乌鲁木齐 834000）

顺北一区油气井垂深大、井筒温度高，部分井最高温度超过170 ℃，而国内现有测量仪器的抗温能力在155 ℃左右。循环温度超过测量仪器抗温能力时，会出现探管烧毁和无信号等问题，影响小井眼超深井的钻井安全和效率。因此，需要研究井筒循环温度场分布及其变化规律。

目前，主要用解析法[1–2]和数值法[3–5]分析井筒温度分布规律，并取得了许多较有代表性的研究成果[6–8]。其中，G.P.Willhite[8]基于井筒非稳态换热机理，考虑井筒流体的热对流、钻柱轴向热传导、钻柱与流体对流换热，以及套管、水泥环、地层间的热交换作用，根据能量守恒原理，运用数值法建立了井筒温度场的微分方程控制组，采用有限差分、有限体积或有限元方法求解；并且，进一步考虑了摩擦热[9]、轴向导热和钻井液径向温度梯度、套管下深长度及溢流[10]等因素的影响，使计算结果更接近于实际。

为了更好地解决顺北一区小井眼超深井存在的问题，笔者首先以Willhite模型[8]为基础，参照顺北一区某水平井，建立了井筒瞬态温度场数学模型，通过分析参数对井筒循环温度的影响规律[11–12]，提出了“临界温度井深”概念；然后基于该概念，对钻井液的流变性、热属性、排量、入口温度和钻柱的热属性等7个参数进行了敏感性分析，绘制了临界温度井深综合图版；最终得到了2种可有效降低顺北一区小井眼超深井井底循环温度的施工方案[13–15]。

1 小井眼超深井井筒温度场理论基础

1.1 物理模型

小井眼超深井钻井过程中，钻井液在井筒内的循环主要分下行和上行2个阶段[16]。

1）下行阶段。钻柱内的钻井液一方面与环空中上返的高温钻井液进行热交换；另一方面因流体黏性耗散而产生热量Qc，使得钻柱内温度升高。

2）上行阶段。环空中钻井液将一部分热量（Qap）传递给钻柱内钻井液，并与井壁、地层之间进行热交换（Qla），同时钻井液还因流动摩擦而产生热量Qa。整个过程中，可将井筒–地层传热系统简化为钻柱内、钻柱壁、环空内和地层等4层结构。井下各控制单元热交换物理模型及网格划分如图1所示（图1中：Qc为钻柱内摩阻产生的热量， W /m；Qa为环空内摩阻产生的热量， W /m；Qap为环空中钻井液传递给钻柱内钻井液的热量， W /m；Qla为地层传递给环空中钻井液的热量， W /m；j为井筒轴线方向的空间节点；i为井筒径向方向的空间节点； Δr为径向步长， m ； Δz为轴向步长， m ；m为径向上单元数；n为轴向上单元数； θij为径向上第i个、轴向上第j个单元格的温度，℃）。

图1 井下各控制单元热交换物理模型及网格划分Fig.1 Physical model of heat exchange and grid division for each downhole unit

1.2 数学模型及求解

1.2.1 数学模型

根据小井眼超深井钻井过程中井筒内钻井液的循环特点及井筒与地层之间的传热机理，对所建物理模型作如下基本假设：1）井筒内钻井液只考虑轴向和径向对流换热；2）井下介质的导热率和比热容为常数，不受温度影响；3）忽略钻井液径向温度梯度与轴向热传导对井筒温度分布的影响；4）地温梯度恒定，并且距井筒无限远处的地层温度不受井筒内传热过程的影响。

基于以上物理模型和假设，可对各个控制单元建立相应的数学模型：

1）钻柱内传热模型。钻柱内钻井液控制单元的热量由4部分组成：轴向上钻井液向下流动携带进入的净热量，径向上钻井液与钻柱壁对流换热产生的热量，钻进中外界对单元体内钻井液所做的功，钻井液内能的变化。由能量守恒原理可得：

2）钻柱壁传热模型。该控制单元的热量由3部分组成：钻柱在轴向上由热传导产生的热量，在径向上与钻柱内和环空钻井液对流换热交换的热量，单位时间内单元体内能的变化量。同理，由能量守恒原理可得：

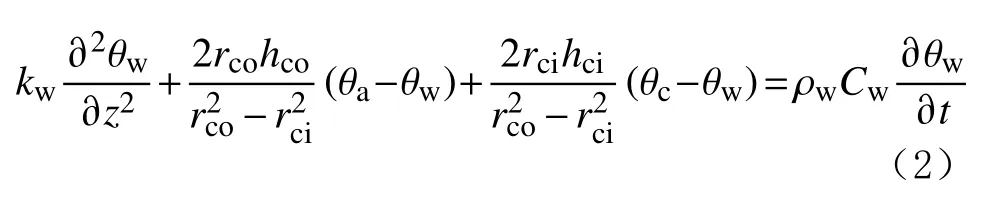
3）环空传热模型。影响环空钻井液热量的因素包括4方面：轴向上钻井液沿井筒向上流动时携带的净热量，与井壁和钻柱外壁发生对流换热产生的热量，外界因素对单元体内液体所做的功，环空钻井液内能的变化。应用数学模型表示为：

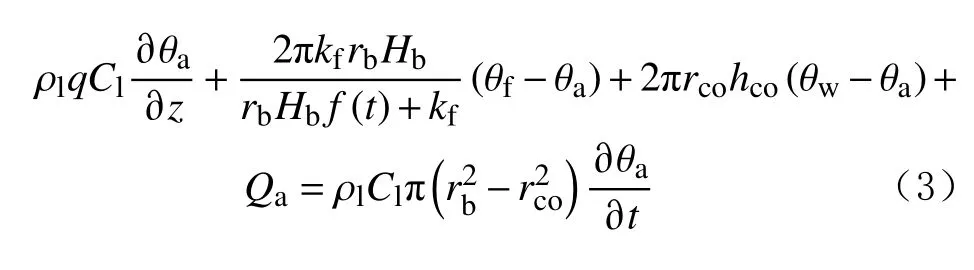
4）地层传热模型。地层单元只考虑径向、轴向热传导，以及自身内能的变化。则数学模型为：

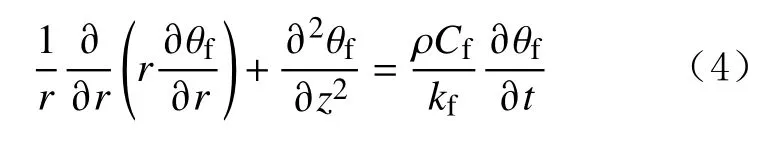
式中： ρl为钻井液密度， k g/m3；q为钻井液质量流量，kg/s；Cl为钻井液比热容，J/(kg·℃)； θc为钻柱内钻井液温度，℃；z为深度，m；rci为 钻柱内半径，m；hci为钻柱壁与钻井液的对流换热系数，W/(m2·℃)； θw为钻柱壁温度，℃；t为时间，s；kw为钻柱材料导热系数，W/(m·℃)；rco为钻柱外半径，m；hco为小井眼钻柱外壁与钻井液的对流换热系数，W/(m2·℃)； θa为环空内钻井液温度，℃； ρw为钻柱材料密度， k g/m3；Cw为钻柱材料比热容，J/(kg·℃)； θf为地层温度，℃；kf为地层导热系数，W/(m·℃)；rb为井眼半径，m；Hb为地层环空交界面与环空内钻井液的对流换热系数，W/(m2·℃)；r为径向距离，m； ρ为岩石密度， k g/m3；Cf为地层岩石比热容，J/(kg·℃)。

在井斜角不为0的井段，各控制单元间的热交换及内能变化与直井段没有本质区别，仅需要在计算过程中对地层温度做相应调整。因此，同样可以采用式（1）—式（4）进行计算。

1.2.2 数学模型求解方法

为求解式（1）—式（4），对物理模型进行了网格划分（见图1）[17]：在井筒径向方向上依次划分了钻柱内、钻柱壁、环空、井壁和套管5个单元格；地层区域按步长为 Δr划分，共在纵向上划分为m个单元格；井筒轴线方向，则将模型从井口到井底按步长为 Δz划分为n个单元格。

基于上述网格划分，利用有限差分法对所建立的数学模型进行空间和时间的离散，使数学模型转化为数值模型。从稳定性角度考虑，对偏微分方程进行全隐式差分处理，其中，微分方程中的一阶空间导数采用一阶迎风格式，一阶时间导数采用两点向后差分，二阶空间导数采用三点中心差分。然后，按照径向上从井眼中心到地层、轴向上从井口到井底和时间上从小到大的次序，将温度变量依次合并。对于每个控制单元，离散方程均可用以下形式表示[18]：

式中：w为时间节点； αij～ ζij为控制体温度系数。

一维网格上所有节点离散方程组成的代数方程组，构成了井筒温度模型差分格式，采用高斯–赛德尔迭代方法进行求解，可得出每一时刻每一控制体的温度。

1.3 模型验证

为验证井筒温度场模型的可靠性，用顺北一区某水平井的数据进行了检验[19]。该井四开采用ϕ120.7 mm钻头钻进，完钻井深 7 778.10 m、垂深 7 569.50 m；钻井液密度 1.32 kg/L，塑性黏度 22 mPa·s，动切力 7 Pa，排量 10 L/s；钻井液入口温度 33 ℃，地表温度 10 ℃，井底电测温度165.97 ℃，地温梯度2.1 ℃/100m。地层、钻井液等传热介质的热物性参数见表1。

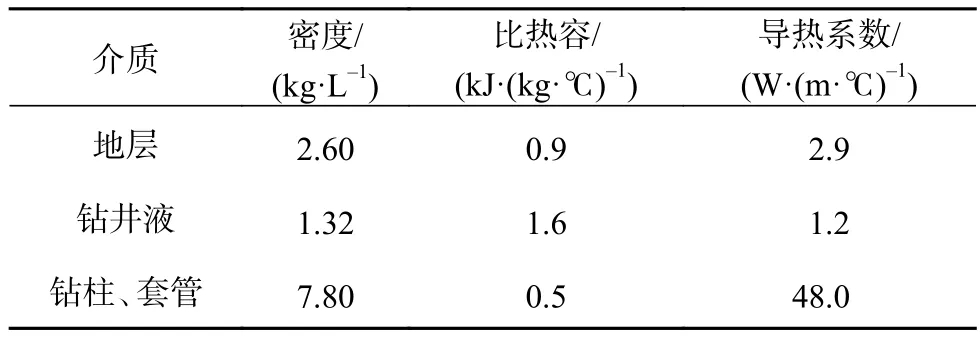
表1 井筒传热介质的热物性参数Table 1 Thermophysical parameters of heat transfer media of the wellbore

仅改变该水平井钻井液的入口温度，循环15 h后的井筒内温度曲线如图2所示。从图2可以看出，当钻井液入口温度由3 ℃升至43 ℃时，井底循环温度在157.63～157.77 ℃，该井所在地区完井电测实测数据为158 ℃左右，二者比较吻合。

图2 不同入口温度下井筒内钻井液的温度变化曲线Fig.2 Temperature variation curves of drilling fluid in the wellbore at different inlet temperatures

由图2可知：1）井筒温度场包括钻柱内和环空2部分，两者的井底循环温度非常接近，且呈现的规律没有本质区别，因此，为讨论整个井段沿钻井液流动方向对井底循环温度的影响，下文均选取钻柱内温度为研究对象；2）尽管钻井液入口温度变化较大，但井底温度几乎恒定在157～158 ℃，该值与入口温度无关。已知井底地层电测温度为165.97 ℃，则井底循环温度相对地层温度仅下降8 ℃左右，难以满足井下仪器工作要求。

2 临界温度井深的概念及类型

2.1 临界温度井深

为分析钻柱内温度相对于地层温度的变化规律，以地层温度为基准，计算了图2中地层温度与钻柱内温度的差值，得到了不同入口温度下钻柱内钻井液温度相对于地层温度的降低值（见图3）。

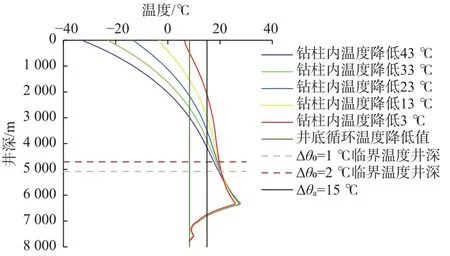
图3 不同入口温度下钻柱内钻井液循环温度相对于地温的降低值Fig.3 Reduction in the circulating temperature of drilling fluid in the drill string relative to ground temperature at different inlet temperatures

图3呈现出一个明显特征：随着井深增加，各曲线逐渐收敛，并在某一井深处几乎重合（该井深处各曲线对应温度的差值 Δ θ0＜1 ℃）。由此可以给出一般性定义：若改变某一参数，在井深方向上存在一点，该点至井底的钻柱内温度几乎恒定，且井底循环温度相对地层温度降温值不能满足测井仪器的工作要求，则称这点处井深为该参数影响钻柱内温度场的临界井深，简称“临界温度井深”（记为Hc）。

进一步，可以给出临界温度井深存在的一般条件，即：设 Δ θa为井底循环温度与地温差值的最小允许值，当某个参数X在给定区间D=(Xa，Xb)内变化时，井底Hb处的循环温度 θci与地层温度 θfo的差值Δθbf满足式（6），则在区间D内必存在临界温度井深。式（6）的表达式为：

式 中 ： θfo为 井底地层温度，℃； θci为 井 底循环温度，℃； Δ θbf为井底循环温度与地层温度的差值（简称井底循环降温值），℃； Δ θa为井底循环温度与地层温度差值的最小允许值，℃。

由临界温度井深（Hc）的定义可知，Hc反映了某参数影响钻柱内温度的极限深度，是一项定量描述该参数对井筒温度场影响强弱的指标。若某参数对井筒循环温度影响较弱，那么Hc必小于实际井深，此时井底循环温度不能满足测井仪器的工作要求。反之，若该参数对井筒循环温度影响能力强，则Hc有可能等于或超过实际井深，能满足测井仪器的工作要求。由此可见，有效降低小井眼超深井井底循环温度的实质，就是使Hc下移并到达井底。

2.2 临界温度井深类型

2.2.1 真实临界温度井深

根据Hc的存在条件，入口温度在3～43 ℃变化时，井底循环降温值 Δ θbf恒定为8.3 ℃，低于测量仪器允许的最小值 Δ θa（该井 Δ θa约为15 ℃），满足式（6），则存在Hc。 例如，图3中，若 Δ θ0分别取1和2 ℃，则对应的Hc为5 306.40和4 708.50 m。因为此时临界温度井深以浅钻柱内温度变化较大，以深钻柱内温度几乎没有变化，真实反映了钻井液入口温度影响钻柱内温度的极限深度，故称为“真实临界温度井深”，其值取决于 Δ θ0给定值。由图3可抽象出真实临界温度井深的理想曲线（见图4，图中： Δ θ0为各曲线对应温度之间的差值，℃；Hre为真实临界温度井深，m；Xa2，Xb2为钻井液入口温度变化范围的边界值，℃；①，②，③为理想曲线编号）。

图4 真实临界温度井深的理想曲线Fig.4 Ideal curve of true well depth at critical temperature (WDCT)

从图4可以看出，真实临界温度井深的理想曲线以Hre为分界点，上部发散、下部收敛。这是因为，较低的排量和钻柱良好的导热性，使低温钻井液在沿钻柱下行过程中与环空上返的高温钻井液充分进行了热交换；当井深超过Hre时，井筒内热交换达到平衡状态。所以，真实临界温度井深理想曲线代表对井筒循环温度影响较弱的一类参数，尽管这类参数对上部井段钻柱内温度的影响较大，但对Hre以下钻柱内温度场的影响能力极弱。一般此类曲线的井底循环降温值 Δ θbf明显小于测井仪器要求的最小允许值 Δ θa，降温能力有限。

2.2.2 当量临界温度井深

仅改变钻柱导热系数、循环15 h后地层温度与钻柱内温度的差值曲线如图5所示。可以看出，图5与图3中给定情况有明显区别，当钻柱导热系数由48 W/（m·℃）降至 1 W/（m·℃）时，由图3 中 Δ θbf的确定方式可知，此时对应的 Δ θbf由8.32 ℃ 升为31.76 ℃，则井底循环温度由157.65 ℃降为134.20 ℃，可见改变钻柱导热系数对井底循环温度影响极大，井底循环温度下降显著。

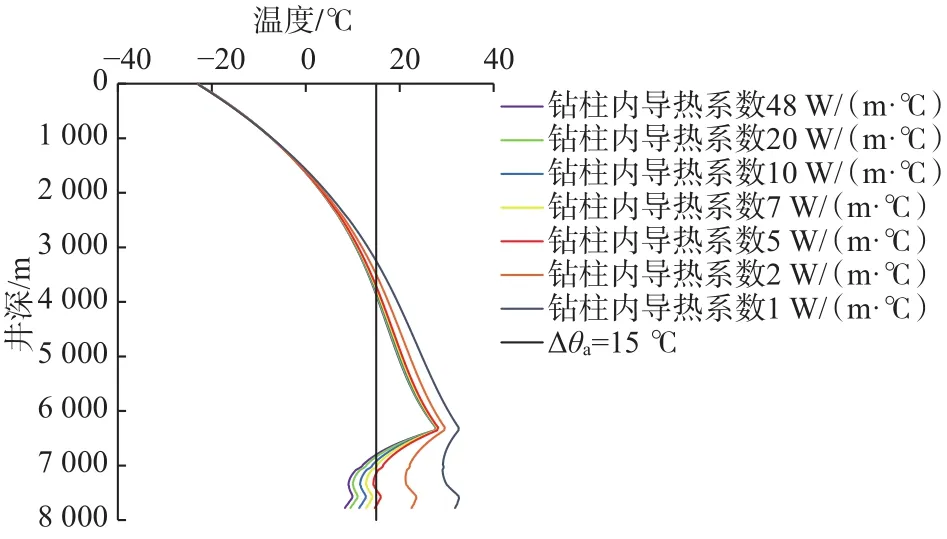
图5 改变钻柱导热系数后钻柱内循环温度相对地温的降低值Fig.5 Reduction in the circulating temperature in the drill string relative to ground temperature after a change in thermal conductivity of the drill string

由图5可知，若 Δ θa取15 ℃，改变钻柱导热系数，部分曲线对应的井底循环降温值 Δ θbf仍然不满足井下测井仪器的工作要求，根据临界温度井深的存在条件（式（6）），此时必存在Hc。为确定此情况下的临界温度井深，抽象出图5的理想曲线（见图6，仅绘制了3条曲线，其中： Δ θbf1， Δ θbf2和 Δ θbf3分别为理想曲线①、②和③对应的井底循环降温值）。

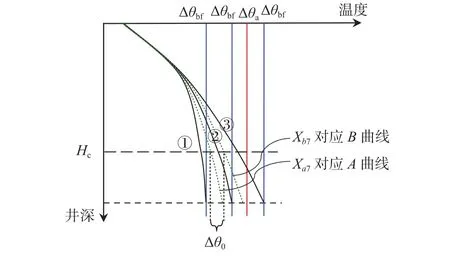
图6 改变钻柱导热系数时的临界温度井深理想曲线Fig.6 Ideal curve of WDCT after a change in thermal conductivity of the drill string

图6中，由于理想曲线①、②对应的井底循环降温值 Δ θbf小于 Δ θa，故必存在Hc。以曲线②为例讨论Hc。设曲线②对应的钻柱导热系数为X7，若给X7一个任意变化区间[Xa7，Xb7]，当X7取边界值Xa7和Xb7时，对应图中曲线A和B。此时，令Xa7→Xb7，则曲线A和B将收敛于理想曲线②，参照真实临界温度井深的确定方法，由 Δ θ0给定值可确定该情况下的临界温度井深为图6中Hc。

深入分析可知，由于图6中理想曲线上部收敛、下部发散，因此确定的临界温度井深并不能直观反映钻柱导热系数影响钻柱内温度的极限深度，此时可根据井底循环温度与地层温度差构建当量临界温度井深的近似计算公式，改写图中的Hc。其近似计算公式为：

式中：Hd为当量临界温度井深，m；H为井筒深度，m。

由式（7）确定的Hd不能由 Δ θ0直接确定，而是在理论上表征该参数对井筒温度场的影响能力，故称为“当量临界温度井深”。

与真实临界温度井深的理想曲线不同，当量临界温度井深的理想曲线刻画了可以显著改变井底循环温度的一类参数，主要包括钻井液比热容、钻井液导热系数和钻柱导热系数。钻井液及钻柱导热系数较小时，低温钻井液沿钻柱下行过程中与环空中钻井液的热交换效率可以降低；钻井液的比热容较高时，钻井液沿钻柱下行过程中，同等排量下能够吸收更多的热量。这样就使到达井底的钻井液仍保持较低温度，进而能够显著降低井底循环温度，故当量临界温度井深理想曲线表现出上部收敛、下部发散的特征。

2.2.3 过渡临界温度井深

除真实临界温度井深和当量临界温度井深外，还存在一种过渡类型，称为“过渡临界温度井深”（记为Hts）。过渡临界温度井深参数主要包括钻井液排量、钻井液塑性黏度和动切力，其理想曲线在整个井深范围内均呈发散状态，井底循环降温值Δθbf在一定范围变化，但一般小于 Δ θa。如钻井液塑性黏度在18～26 m P a·s变化时，井底循环温度在159.52～156.90 ℃。同样，可采用式（7）计算Hts，这里不再讨论。

3 临界温度井深的应用

3.1 井筒温度场敏感性分析

可以把各参数对井底循环温度的影响效果，统一用临界温度井深进行表征, 进而分析各参数对临界温度井深的影响规律，最终为顺北一区油气井施工提供参考。为此，取 Δ θa=15 ℃、 Δ θ0=1 ℃，对钻井液、钻柱相关的7个参数取不同值（见表2），得到了对应临界温度井深计算结果（见图7）。

表2 参数Xij的计算取值Table 2 Calculated value of parameter Xij

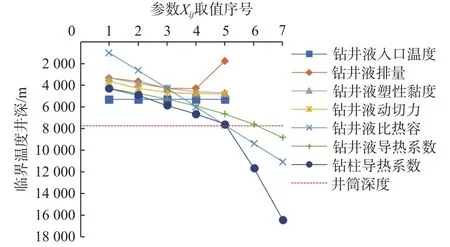
图7 各参数取不同值时对应的临界温度井深Fig.7 WDCTs corresponding to different parameters

图7中的7条曲线可以分为3类（Ⅰ类、Ⅱ类和Ⅲ类）：Ⅰ类曲线的斜率为0（恒定值），参数为钻井液入口温度，对应真实临界温度井深（5 306.40 m）小于实际井深；Ⅱ类曲线的斜率较小，近似水平，参数包括钻井液排量、塑性黏度和动切力，其临界温度井深的变化范围较小，对应过渡临界温度井深（4 811.00 m 以内）小于实际井深；Ⅲ类曲线对应参数为钻井液比热容、钻井液及钻柱的导热系数，曲线斜率变化较大，当量临界温度井深迅速增加，部分超过实际井深，满足井下测井仪器的工作要求。

显然只有Ⅲ类曲线对实际施工具有参考意义，为便于现场计算，可回归出Hd分别与钻井液比热容（X5）、钻井液导热系数（X6）及钻柱导热系数（X7）的关系，表达式为：

由式（8）可知，当量临界温度井深对3个参数的敏感程度为：钻柱导热系数＞钻井液比热容＞钻井液导热系数。实际应用中，采用式（8）可以快速近似计算Hd。

综上所述，各参数对临界温度井深影响情况的综合分析结果见表3。

根据表3，对于顺北一区小井眼超深井，降低井底循环温度的方式首推改变钻井液热属性，即改变钻井液的比热容和导热系数，该方式的降温效率满足要求，但对钻井液性能要求较高；其次推荐降低钻柱导热系数，该方式虽然降温效率显著，且对钻井液性能要求较低，但需要开展钻柱隔热涂层技术研究，施工难度较高。

表3 各参数对临界温度井深影响情况的综合分析结果Table 3 Comprehensive analysis results of each parameter's effect on WDCT

3.2 临界温度井深综合图版

综上可知，钻柱导热系数、钻井液比热容和钻井液导热系数对Hd影响显著，同时由于井底循环温度往往是多个因素综合作用的结果，因此为便于观察同时改变上述3参数时Hd的变化规律，绘制了当量临界温度井深变化图版（见图8—图11）。

图8—图11均可划分为2个区域：黄色区域（Hd已下移至井底）和非黄色区域（Hd未下移至井底）。现场应用中，要通过调整相关参数，使所得Hd落入黄色区域内。例如，当钻柱、钻井液的导热系数分别为 48 和 0.9 W/（m·℃）时，由图8 可知钻井液比热容若取 1.4，1.6 和 1.8 kJ/（kg·℃），对应的Hd分别为 3 987.40，5 922.60 和 7 778.10 m。显然，在上述参数下，钻井液比热容取值大于1.8 kJ/（kg·℃），即可使Hd下移至井底；同理，当钻柱导热系数、钻井液比热容分别为 48 W/（m·℃）、2 kJ/（kg·℃）时，钻井液导热系数取值需小于1.1 W/（m·℃）才能满足要求。同时分析图8—图11，可以得出2条明显的规律：

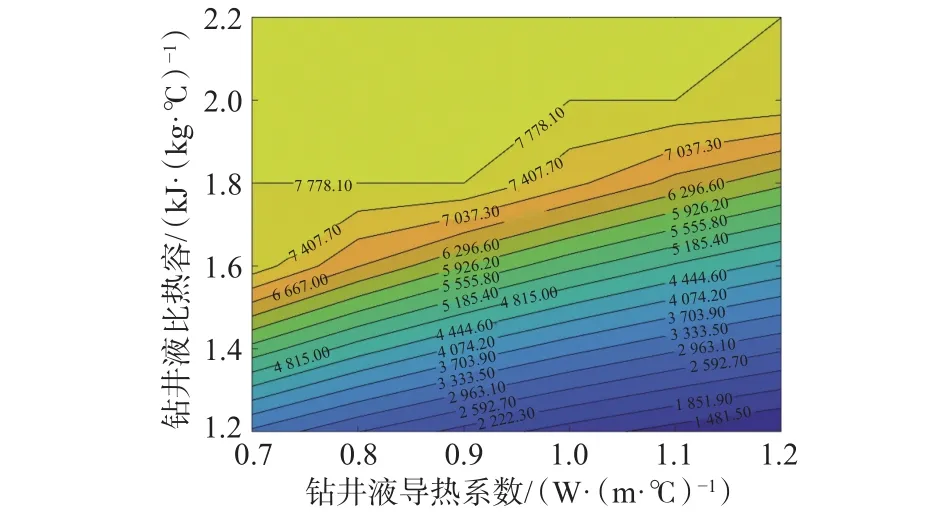
图8 钻柱导热系数为48 W/(m·℃)时的临界温度井深图版Fig.8 WDCT at a thermal conductivity of 48 W/(m·℃) of the drill string

图11 钻柱导热系数为2 W/(m·℃)时的临界温度井深图版Fig.11 WDCT at a thermal conductivity of 2 W/(m·℃) of the drill string

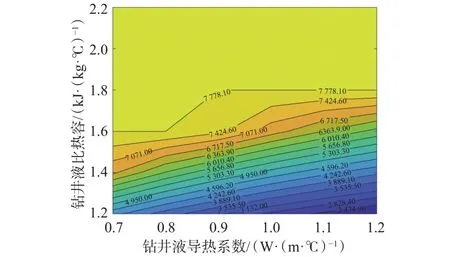
图9 钻柱导热系数为10 W/(m·℃)时的临界温度井深图版Fig.9 WDCT at a thermal conductivity of 10 W/(m·℃) of the drill string

1）Hd的等势线斜率较小，说明在不同钻柱导热系数下，钻井液的比热容、导热系数取值在正常范围时，提高钻井液比热容比降低钻井液导热系数更容易使Hd下移至井底；

图10 钻柱导热系数为5 W/(m·℃)时的临界温度井深图版Fig.10 WDCT at a thermal conductivity of 5 W/(m·℃) of the drill string

2）随着钻柱导热系数由 48 W/（m·℃）降至2 W/（m·℃），图中黄色区域面积迅速增大，可见若能降低钻柱导热系数，能够使Hd下移至井底，则在施工中可以极大地降低对钻井液性能的要求。

4 结论与建议

1）顺北一区小井眼超深井井筒温度高，部分井温度超过国内现有测量仪器抗温能力，易导致测量仪器探管烧毁和无信号等问题，严重制约了钻井效率的提升，需要对其井筒循环温度场分布及其变化规律进行研究。

2）根据不同参数对井筒温度场的影响大小，提出了临界温度井深的概念，并分析指出了有效降低小井眼超深井井底循环温度的机理——使临界温度井深下移并到达井底。可应用临界温度井深对井筒温度场进行敏感性分析。

3）敏感性分析结果表明，井筒温度场对3个参数较为敏感，其敏感程度为：钻柱导热系数＞钻井液比热容＞钻井液导热系数。顺北一区小井眼超深井采用改变钻井液热属性或降低钻柱导热系数的方式，可以有效降低井底循环温度。

4）考虑技术和施工难度，建议进一步加强对钻井液性能、钻柱隔热材料的研究。