试样原始横截面积计算方法对抗拉强度的影响
薛 凯, 历 妍, 王毅磊
(宝钢湛江钢铁有限公司 制造管理部, 湛江 524072)
抗拉强度是金属材料重要的力学性能指标之一,通过拉伸试验起始拉伸到断裂过程中的最大拉伸力和试样原始横截面积之比来计算[1]。GB /T 228.1-2010《金属材料拉伸试验第1 部分: 室温试验方法》中规定“宜在试样平行长度中心区域以足够点数测量试样的相关尺寸”、“原始横截面积S0是平均横截面积,应根据测量的尺寸计算”[2]。ISO 6892-1:2019(E)与JIS Z2241:2011相较于GB /T 228.1-2010对于原始横截面积多出了“建议至少测量3点的相关尺寸”[3-4]。而ASTM E8/E8M-16a中也说到“允许试样平行段从两端向中间逐步减小,形成一个锥度”[5]。因此,笔者认为试样横截面积只需在试样标距中心测量计算,即测量试样标距中心的宽度和厚度。在实际生产中,因试样的断裂位置并不一定就是所测得最小横截面积处[6],且冷轧薄板在拉伸时需同时检测钢板的应变强化指数(r值)等性能,需要试样的实际宽度的平均值来计算,而拉伸试验需在试样标距中间分别测量3组试样的宽、厚度并计算横截面积,对于试验工作量大、自动化程度不高的试验室,需要记录的原始数据量很大,在实际执行过程中可操作性不强,有文献建议在标准中明确使用多个测量位置的宽度平均值与厚度平均值的乘积作为平均横截面积[7]。笔者通过试验来分析试样不同横截面积的计算方法(即在测量计算原始横截面积时,在试样标距两端及中间分别测量试样的宽厚度,选取3点横截面积的平均值、3点横截面积中的最小值或3点宽度平均值和厚度平均值的乘积)对抗拉强度测试结果的影响。
1 试验方法
1.1 试样制备
试样加工为拉伸试验中的P6试样,具体信息见表1[8]。
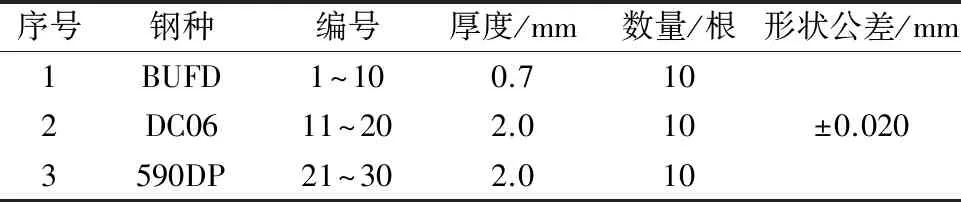
表1 试样信息Tab.1 Sample information
1.2 试验设备
试验采用全自动电子拉伸试验机,力值测量范围为0~150 kN,测量精度为0.5级,横截面测量仪精度为±1.0 μm。
1.3 试验方法
测量表1中拉伸试样标距两端及中间的宽厚度,再按GB/T 228.1-2010的方法B在拉伸试验机上拉伸至断裂,记录试验过程中的最大力值后,再计算不同原始横截面积的计算方法所对应的抗拉强度值。
1.4 原始横截面积及对应抗拉强度的计算
原始横截面积及对应抗拉强度按以下几种方法计算:
(1) 面积的平均值S01:在标距两端及中间选取3点测量试样的宽度和厚度,分别计算3点的横截面积,再求横截面积的平均值;通过试样拉断过程中的最大力,求得其抗拉强度Rm1。
(2) 宽厚度平均值的乘积S02:在标距两端及中间选取3点测量试样的宽度和厚度,计算3点宽度和厚度的平均值,再计算宽度和厚度平均值的面积;通过试样拉断过程中的最大力,求得其抗拉强度Rm2。
(3) 面积的最小值S03:在标距两端及中间选取3点测量试样的宽度和厚度,分别计算3点的横截面积;通过试样拉断过程中的最大力,求得其抗拉强度Rm3。
(4) 采用试样名义宽度时面积的平均值S04:名义宽度为20 mm的试样,在标距两端及中间选取3点测量试样的宽度和厚度,尺寸公差和形状公差分别在±0.10 mm和0.12 mm内,采用试样的名义宽度分别计算3点的横截面积,再求横截面积的平均值;通过试样拉断过程中的最大力,求得其抗拉强度Rm4。
(5) 试样形状公差接近极限时面积的平均值S05:名义宽度为20 mm的试样,在标距两端及中间选取3点测量试样的宽度和厚度,假设试样在标距部分内,形状公差恰好等于0.12 mm,分别计算3点的横截面积,再求横截面积的平均值;通过试样拉断过程中的最大力,求得其抗拉强度Rm5。
(6) 测量试样标距中间时的原始横截面积S06:通过测量标距中间的宽度和厚度计算试样的原始横截面积;通过试样拉断过程中的最大力,求得其抗拉强度Rm6。
2 试验结果与讨论
2.1 横截面积及抗拉强度结果
横截面积计算平均值及抗拉强度试验结果见表2和表3。
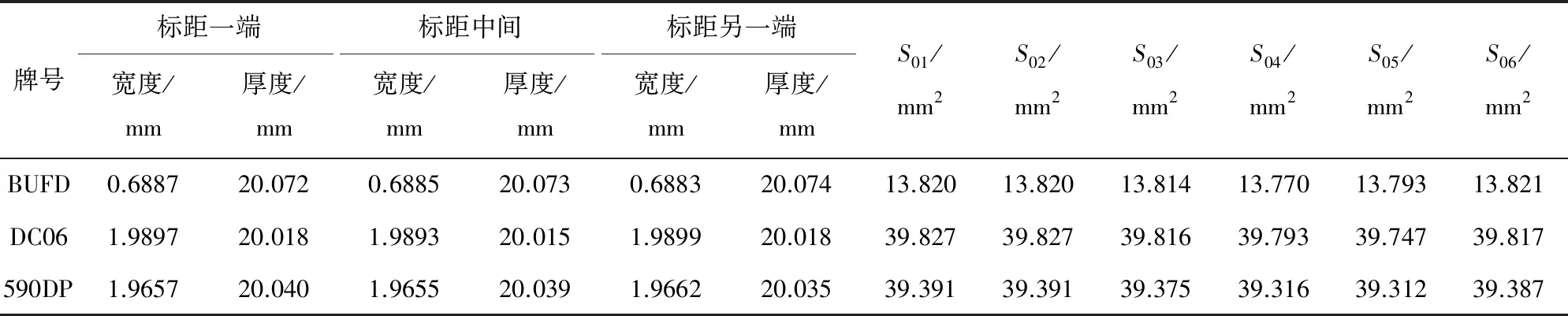
表2 拉伸试样原始横截面积均值表Tab.2 Average value of original cross section area of tensile samples
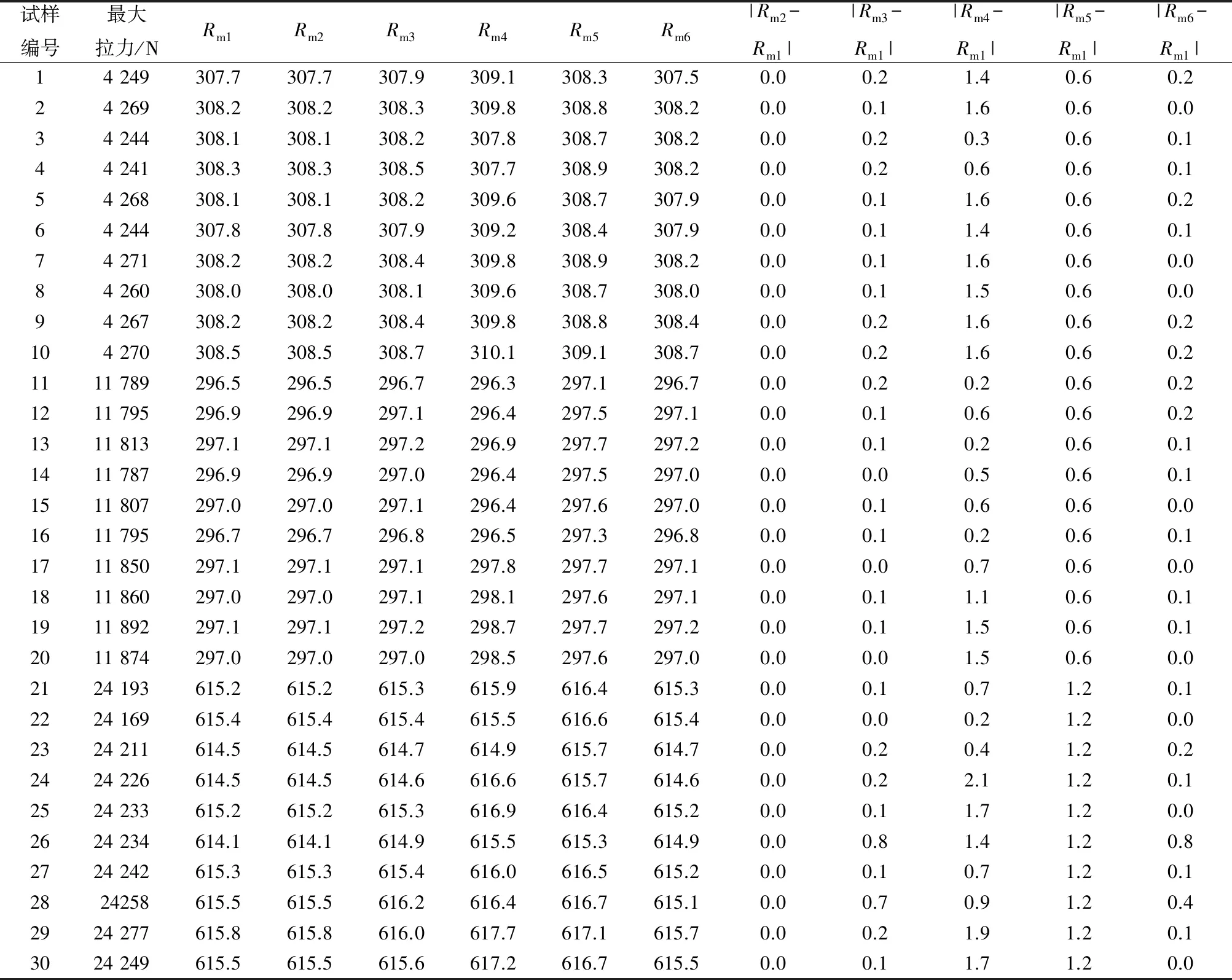
表3 拉伸试样抗拉强度测试结果Tab.3 Tensile strength test results of tensile samples MPa
2.2 试验结果分析
不同材料的不同横截面积计算方法得到的原始横截面积如图1和图2所示,可见面积的平均值S01与宽厚度平均值的乘积S02结果重合,S02,S03,S06与S01的差值比S04,S05与S01的差异小。不同材料试样的不同横截面积计算方式得到的抗拉强度如图3~图5所示。

图1 BUFD钢试样不同原始横截面积计算方法所得的结果Fig.1 Results obtained by different original cross section area calculation methods of BUFD steel samples
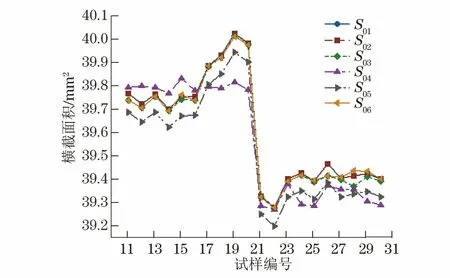
图2 DC06钢与590DP钢试样不同横截面积计算方法所得的结果Fig.2 Results obtained by different original cross section area calculation methods of DC06 steel and 590DP steel samples

图3 BUFD钢试样不同横截面积计算方法所得的抗拉强度Fig.3 The tensile strength obtained by different original cross section area calculation methods of BUFD steel sample
分析图3和图4可知,在强度相近时,不同厚度的材料采用宽厚度平均值的面积计算的Rm2与面积平均值计算的Rm1没有区别,且Rm2,Rm3,Rm6与Rm1的差值都小于Rm4,Rm5与Rm1的差值。
分析图4和图5可知,在厚度相近时,不同强度的材料采用宽厚度平均值的面积计算的Rm2与面积平均值计算的Rm1没有区别,且Rm2,Rm3,Rm6与Rm1的差值都小于Rm4,Rm5与Rm1的差值;
分析图3、图4和图5可知,宽厚度平均值的面积计算的Rm2与面积平均值计算的Rm1差值几乎为0,与面积最小值计算的Rm3,Rm6极差仅仅只有0.8 MPa,但都小于采用试样名义宽度或达到试样极限形状公差时所计算的强度Rm4和Rm5与Rm1的差值。

图4 DC06钢试样不同横截面积计算方法所得的抗拉强度Fig.4 The tensile strength obtained by different original cross section area calculation methods of DC06 steel sample
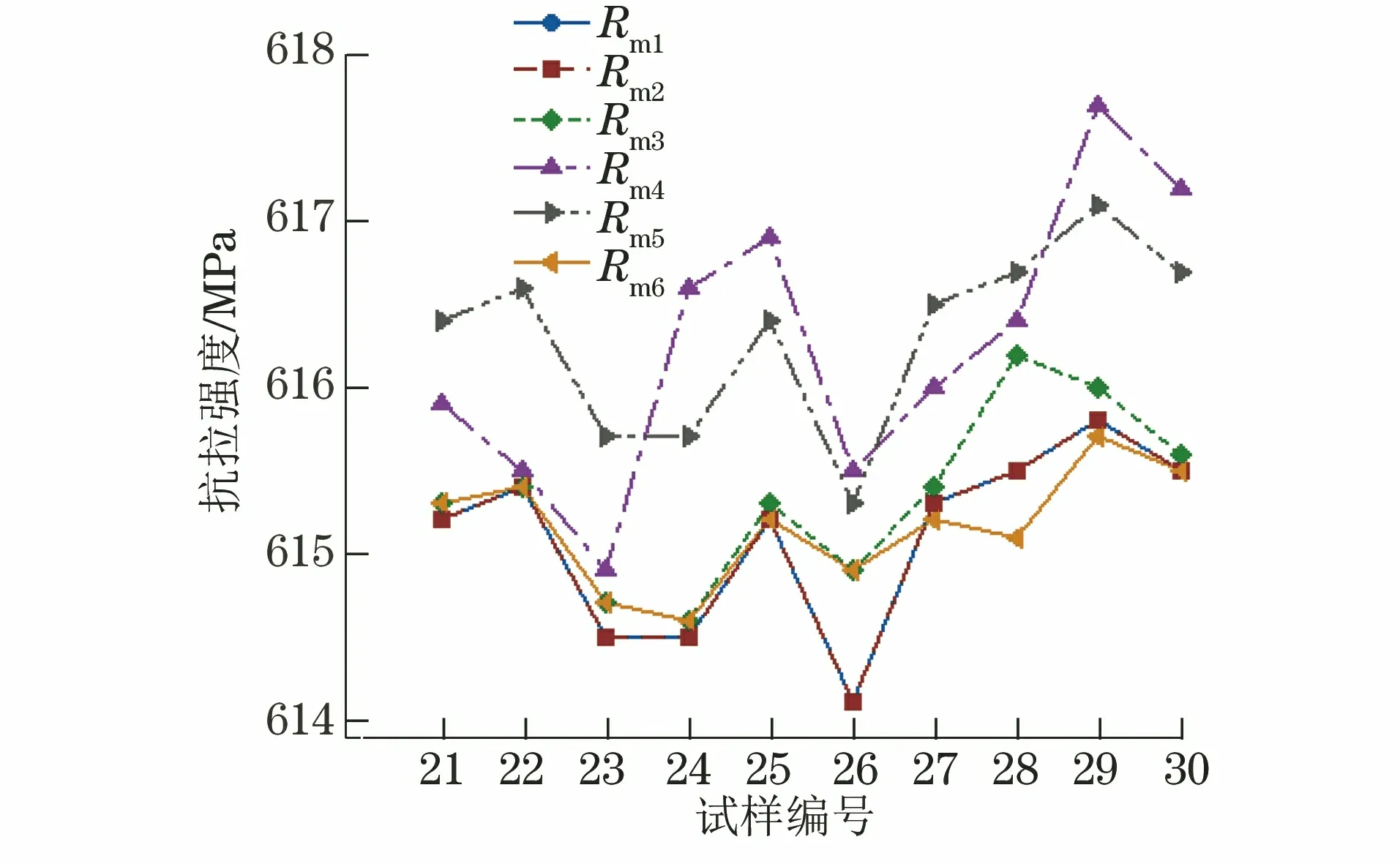
图5 590DP钢试样不同横截面积计算方法所得的抗拉强度Fig.5 The tensile strength obtained by different original cross section area calculation methods of 590DP steel sample
为了分析不同横截面积计算方法得到的抗拉强度是否存在显著性差异,将表3中不同原始横截面积计算方法所得到的的抗拉强度进行F检验和t检验,结果见表4。采用宽厚度平均值的乘积S02及面积平均值S01计算的抗拉强度结果重合,采用宽厚度平均值的乘积S02,面积最小值S03及原始横截面积S06计算的抗拉强度与面积平均值S01计算的抗拉强度无显著差异。而采用S04及S05计算的抗拉强度与采用S01计算的抗拉强度存在显著性差异。
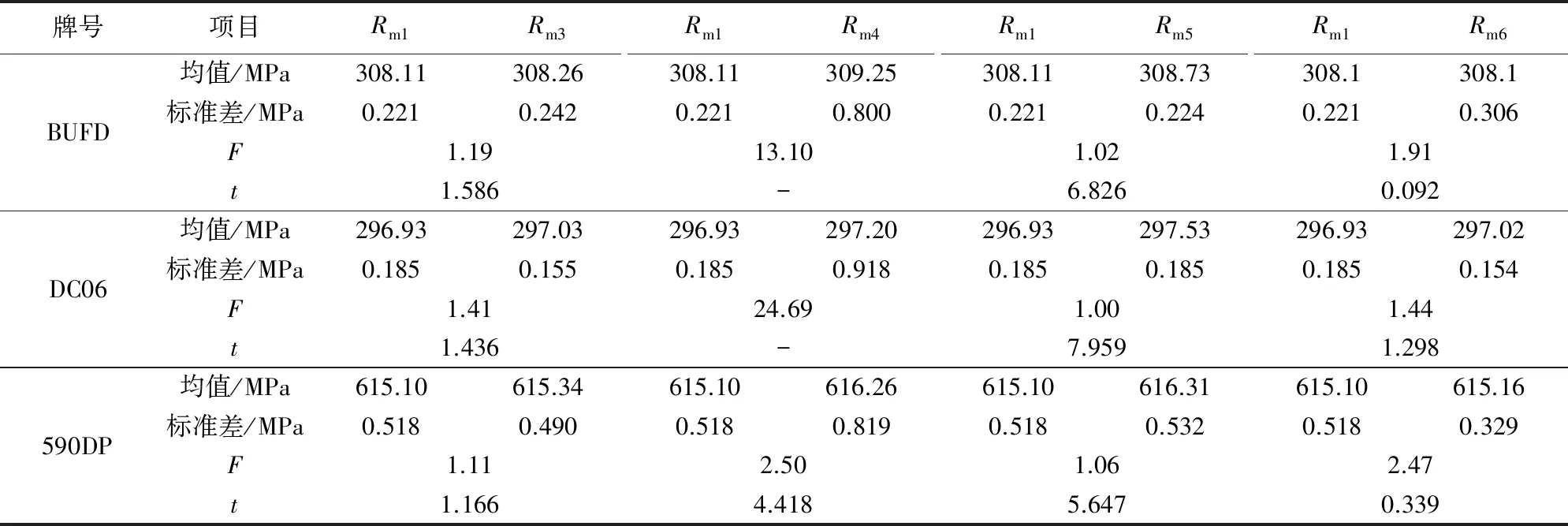
表4 抗拉强度的F检验和t检验统计表Tab.4 Statistical table of F test and t test for tensile strength
4 结论及建议
在形状公差良好的情况下,对于不同厚度、不同强度的试样,采用宽厚度平均值的乘积、面积平均值、面积最小值或在试样标距中间测量横截面积所计算的抗拉强度无显著差异。试验室可以根据实际情况选择测量点数和计算方法。
通过宽厚度实测尺寸平均值的乘积、面积的平均值、面积的最小值计算得到的抗拉强度与GB/T 228.1-2010中建议采用的通过名义尺寸计算得到的抗拉强度存在显著差异。
建议GB/T 228.1—2010修订过程中,在确定主要技术指标时,要综合考虑生产企业的能力和用户的利益,尤其是对试验工作量大、自动化程度不高的试验室。建议在GB/T 228.1标准中增加采用宽度平均值和厚度平均值的乘积来计算试样原始横截面积的方法。

