岩溶地区地铁盾构隧道下穿既有建筑物施工控制技术*
李 明
(兰州铁道设计院有限公司,730030,兰州 ∥ 高级工程师)
目前,国内对于岩溶地区地铁盾构隧道施工的稳定性研究,以及盾构隧道下穿既有建筑物的施工变形控制技术研究已日趋完善,但关于岩溶地区地铁盾构隧道下穿既有建筑物的研究却相对甚少。文献[5]以昆明地铁4号线联大街站—吴家营站区间盾构隧道施工为背景,采取物探钻孔与电磁波CT(计算机断层扫描)勘察盾构区间内溶洞的具体分布,并利用数值模拟方法分析不同因素对盾构隧道开挖稳定性的影响;文献[6]以长沙地铁3号线盾构下穿某溶岩段为工程背景,通过输入地层与隧道特征参数建立BP(反向传播)神经网络岩溶盾构预测模型,并结合对钻探数据的归纳分析,最终应用于工程实际;文献[7]通过再现“渗流液化-流土漏失”的岩溶塌陷过程,分析地铁隧道穿越岩溶区段的地面塌陷机理,通过构建岩溶塌陷物理模型,提出岩溶处理方案。
本文以广州地铁12号线聚龙站—棠溪站所经过的岩溶地段为工程背景,采用数值分析软件研究不同施工方案、掘进参数对盾构隧道下穿既有建筑物的稳定性影响,以期为岩溶地区盾构下穿既有建筑物施工提供一定借鉴。
1 工程概况
广州地铁12号线(以下简为“12号线”)(见图1)工程自白云区金沙洲起,主要经过白云区、越秀区、海珠区、黄埔区及番禺区大学城,线路全长37.6 km,全线均为地下线。12号线为广州市西北至东南向的骨干线,串联棠溪交通枢纽。其中,聚龙站—棠溪站区间左线长1 557.599 m,右线长1 512.698 m,隧道埋深为20.66~32.91 m,部分地段处于岩溶地区。该区间内下穿众多建筑物,主要有:德康路沿线商铺(5层砖混结构)、棠溪祥岗西新街民房(7层钢筋混凝土结构)、棠溪冲边北街8号住宅(7层钢筋混凝土结构)、棠溪十一社厂房(5层砖混结构)、棠溪祥岗西后街民房(5层钢筋混凝土结构)、创新制服厂(7层钢筋混凝土结构)等。
图1 广州地铁12号线线路走向示意图
聚龙站—棠溪站区间内地层从上往下依次为:填土、粉细砂、淤泥质土、粉质黏土、强风化泥岩、强风化砂岩。各土层物理力学参数见表1。
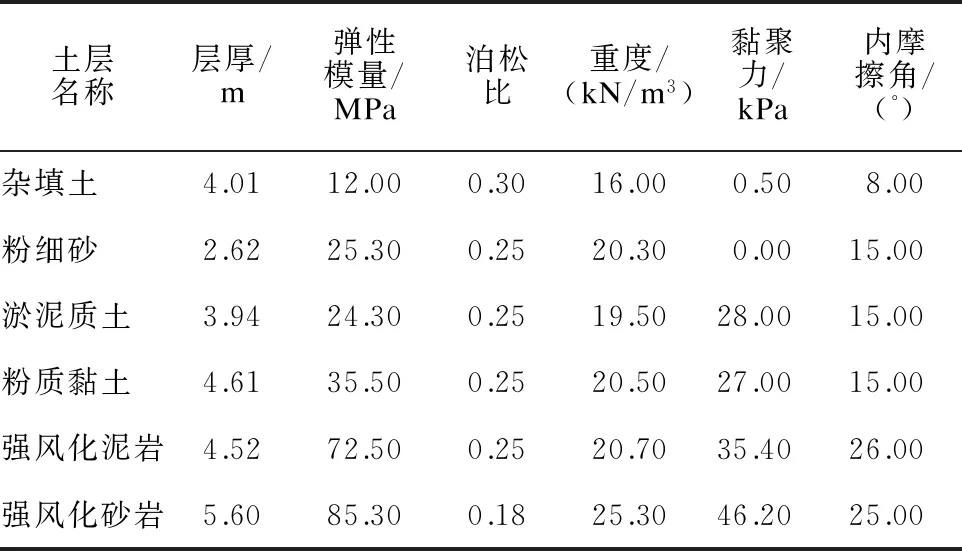
表1 广州地铁12号线聚龙站—棠溪站区间岩溶地段土层的物理力学参数
2 地铁盾构隧道施工影响因素分析
2.1 计算模型建立
采用ANSYS软件建立三维计算模型,运用FLAC3D软件进行隧道开挖的模拟计算。模型(见图2)左右侧边界按距离隧道中线3~5倍的洞径选取,下边界取距离隧道底部3~5倍的洞径,隧道埋深取24.5 m,最终的计算模型尺寸为76 m(x向)×50 m(y向)×62 m(z向)。
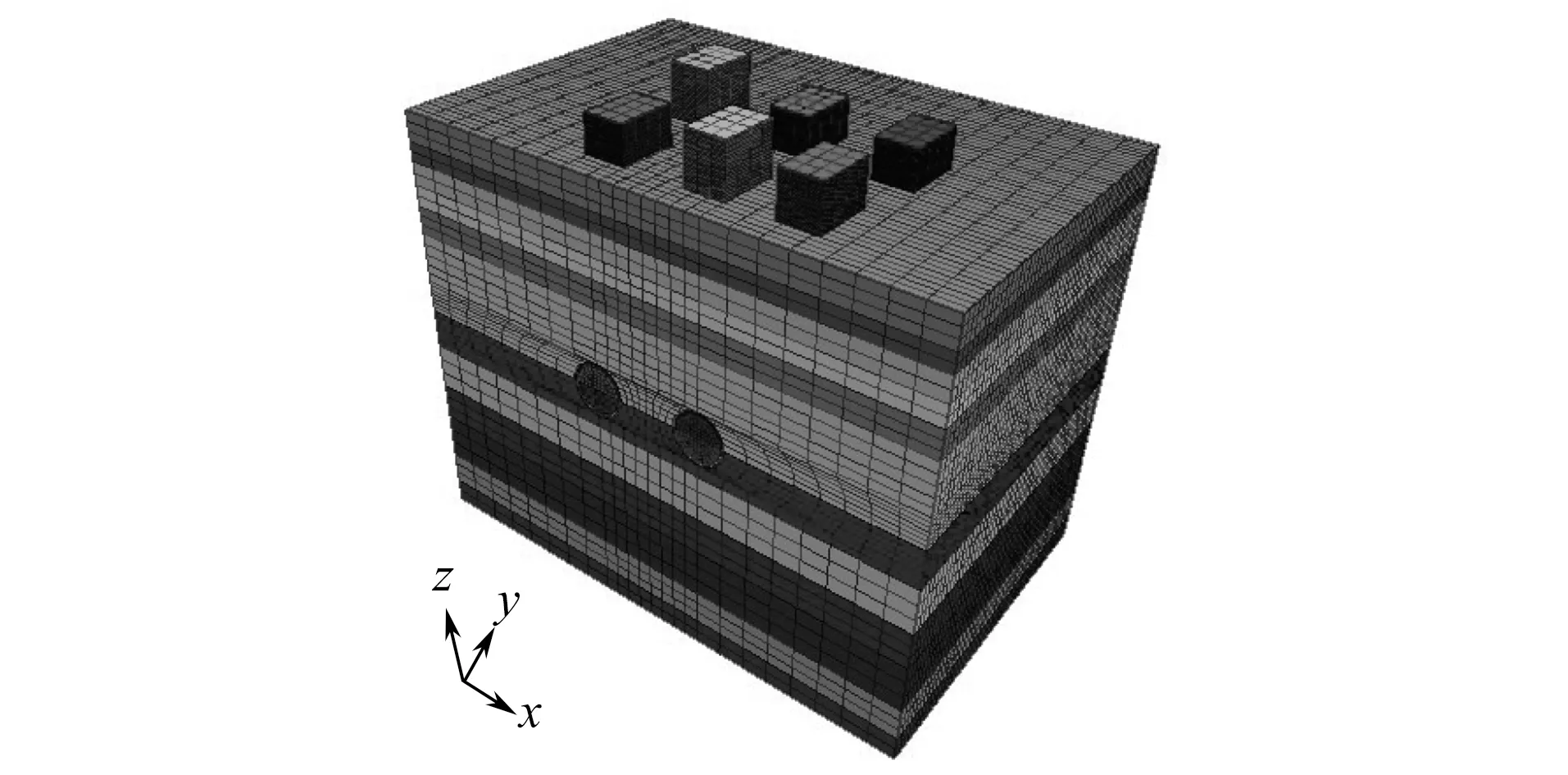
图2 三维计算模型图
岩土体物理力学参数采用表1中所列数据。地表上方建筑物与盾构管片及注浆材料的物理力学参数见表2。
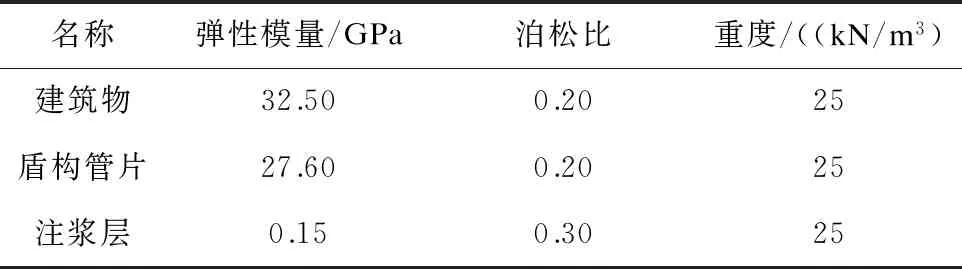
表2 建筑物及盾构衬砌参数
在模型中设置3条监测线,分别距初始开挖面2 m、16 m及32 m;同时对地表既有建筑物进行编号(JZ1—JZ6),并分别取每个建筑物的4个角点(a、b、c、d)进行监测。地表监测线及监测点示意见图3。
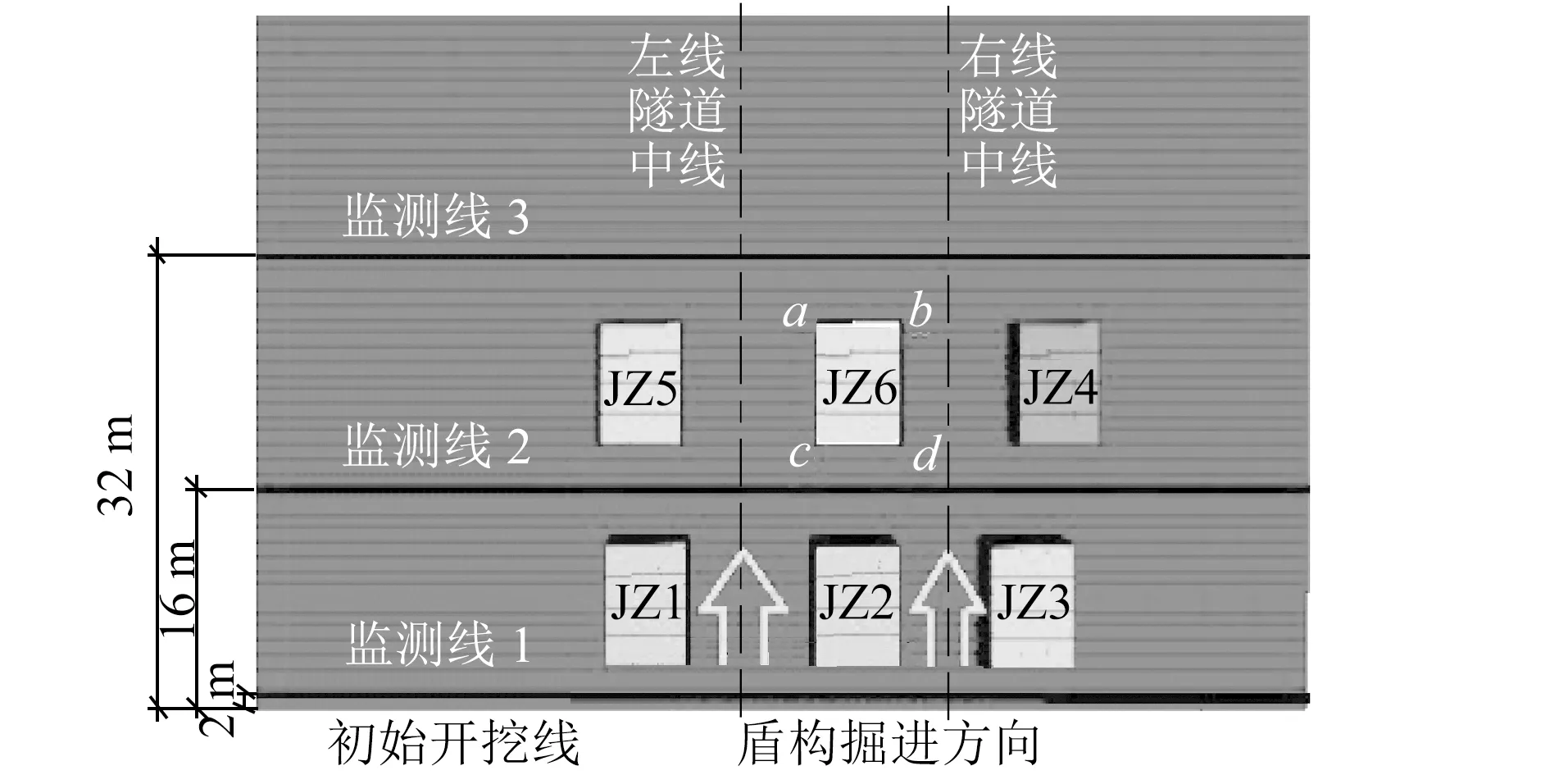
图3 地表监测线和监测点布置示意图
2.2 不同施工工况对既有建筑物的影响
对于双线盾构隧道,施工过程中左右两线的掘进间隔会对上方既有建筑物的地基沉降产生不同的影响。建立的4种工况分别为:①工况1:左右线同时施工;②工况2:右线施工16 m后,左线再行施工;③工况3:右线施工32 m后,左线再行施工;④工况4:右线贯通后,左线再行施工。建立的4 个施工阶段分别为:①右线掘进至监测线2处(隧道掘进至既有建筑之间)(见图3);②右线掘进至监测线3处(隧道掘进穿出既有建筑物)(见图3);③右线贯通;④双线贯通。
由图4可知,双线盾构隧道各施工阶段中,工况1与其他工况相比其地表的最大沉降值均为最大,而工况4与其他工况相比其地表的最大沉降值均为最小;地表沉降的最大值随两线施工间隔的增大逐渐减小。当两线隧道施工间隔增大时,地表沉降最大值会偏向于先行施工的一方;随着两线隧道施工间距减小,地表沉降最大值逐渐向两隧道的中线偏移。由此可见,双线盾构隧道施工间距对施工时产生的地表沉降影响较大,施工中控制好施工间隔就可以一定程度地控制地表沉降。
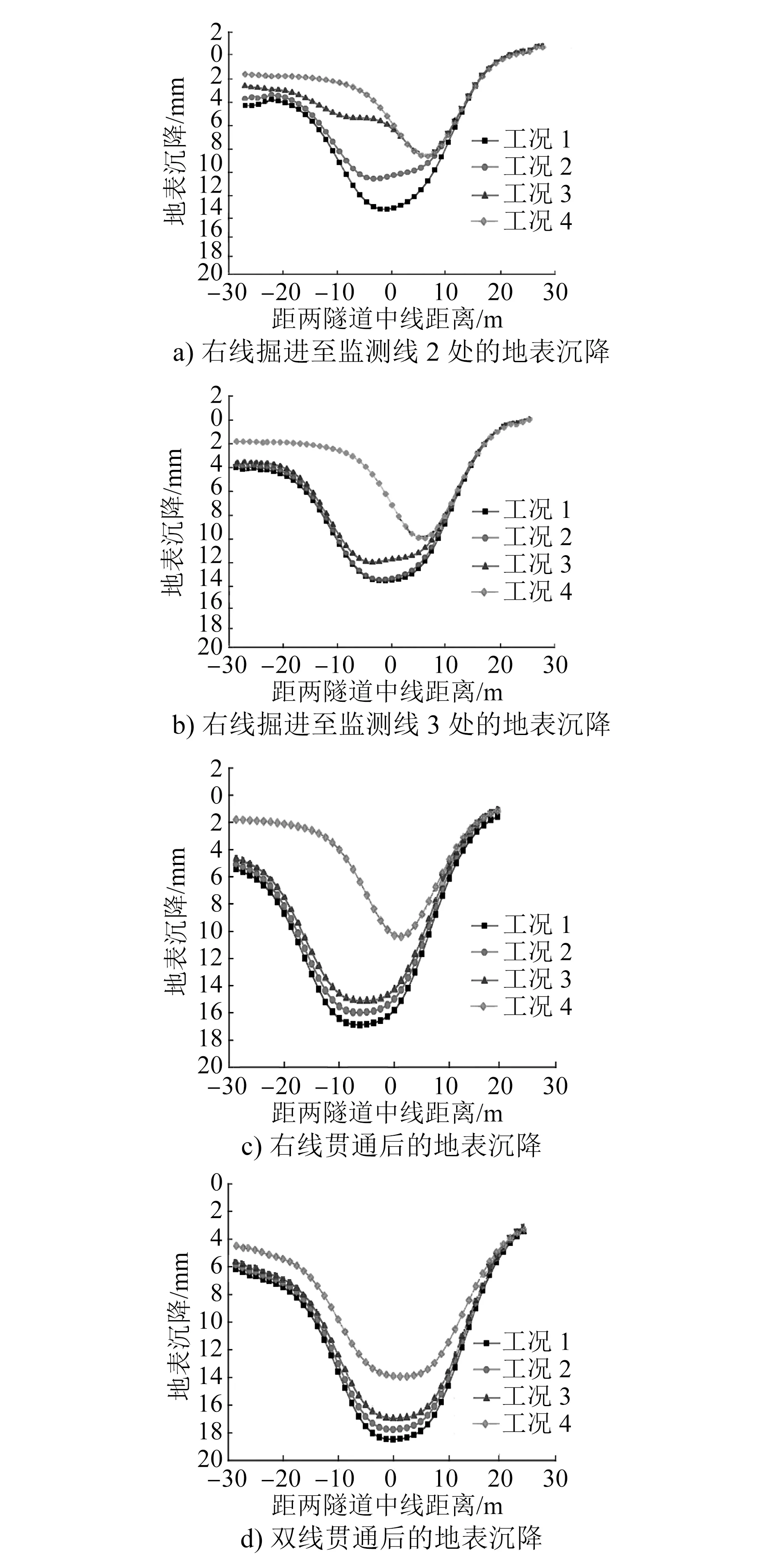
图4 地铁盾构不同施工阶段各工况下的地表沉降曲线
对比4种工况下地表沉降的最大值可知:双线贯通后不同施工间隔下地表沉降规律基本一致;工况1下地表的最大沉降值为18.89 mm;工况2下地表的最大沉降量为17.01 mm,较工况1 时减小了9.95%;工况3下地表的最大沉降量为16.68 mm,较工况1 时减小了11.70%;工况4下地表的最大沉降量为13.99 mm,较工况1时减小了25.93%。综上所述,从控制地表沉降而言,建议采用工况4。
2.3 不同掘进参数对既有建筑物的影响
2.3.1 掌子面顶推力
根据2.2节所得结论,本节研究在工况4下,掌子面不同顶推力作用对盾构隧道上方既有建筑物沉降的影响,如图5所示。
由图5可知:盾构隧道施工时,掌子面顶推力的大小对地表沉降会产生一定的影响,地表沉降随掌子面顶推力的增大而减小;当顶推力为0.15 MPa时,地表最大沉降值为23.21 mm;当顶推力为0.20 MPa时,地表的最大沉降值为19.8 mm;当顶推力为0.25 MPa时,地表最大沉降值为17.25 mm;当顶推力为0.30 MPa时,地表最大沉降值为14.99 mm。由此可见,掌子面顶推力越大,地表沉降值越小。同时考虑在实际施工中,若盾构机顶推力太大,可能会引起开挖面前方的地表隆起过大,对地表既有建筑物的稳定性也会产生一定的影响;另一方面,若顶推力过大,盾构机的刀盘磨损速度及程度会加快,使刀盘的切削能力降低,故本工程中建议采用0.25 MPa的顶推力。
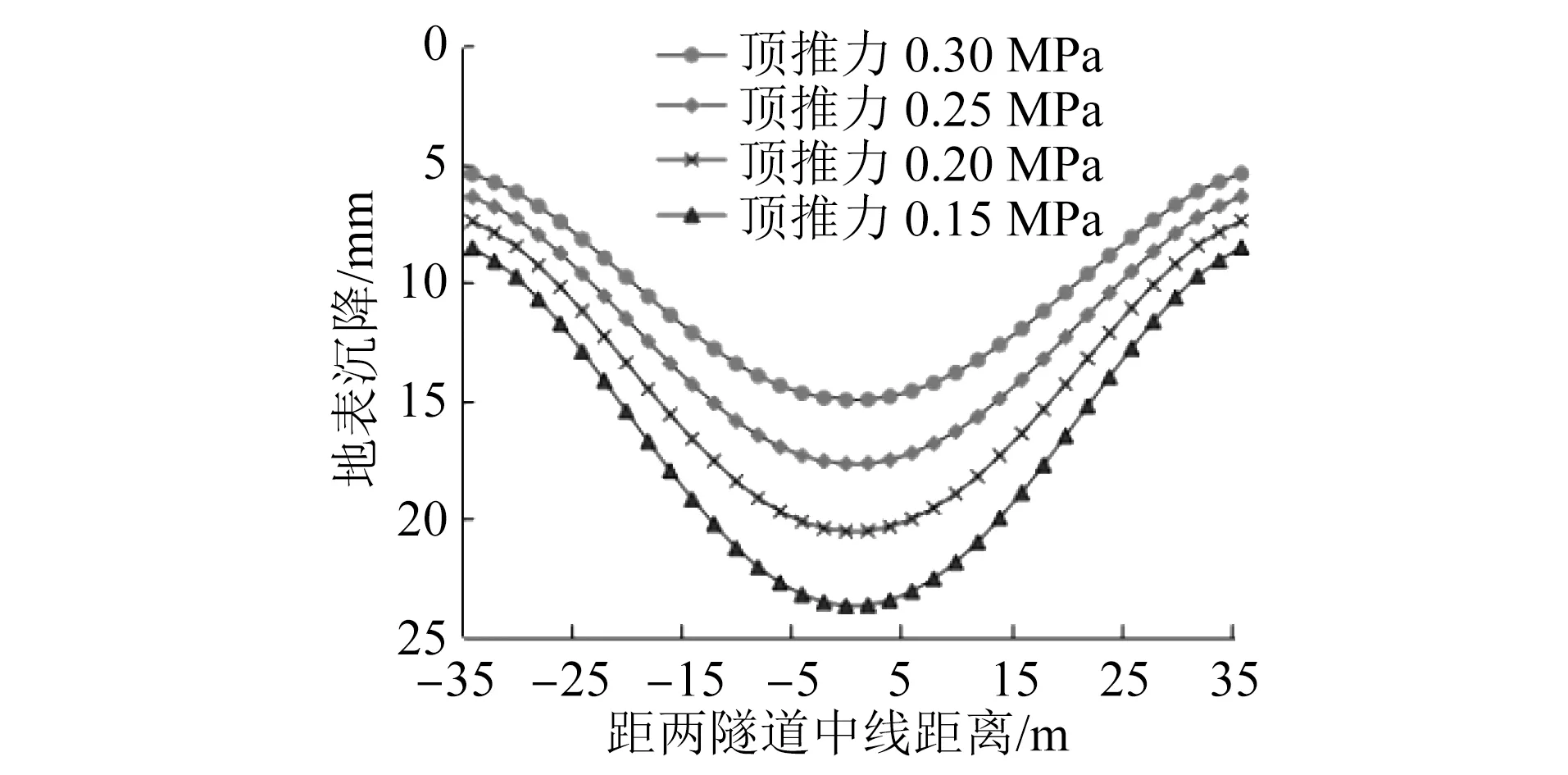
图5 掌子面不同顶推力作用下的地表沉降曲线
2.3.2 注浆压力
在上述研究成果的基础上,考虑掌子面顶推力为0.25 MPa时,不同注浆压力下的地表沉降,其变化曲线如图6所示。
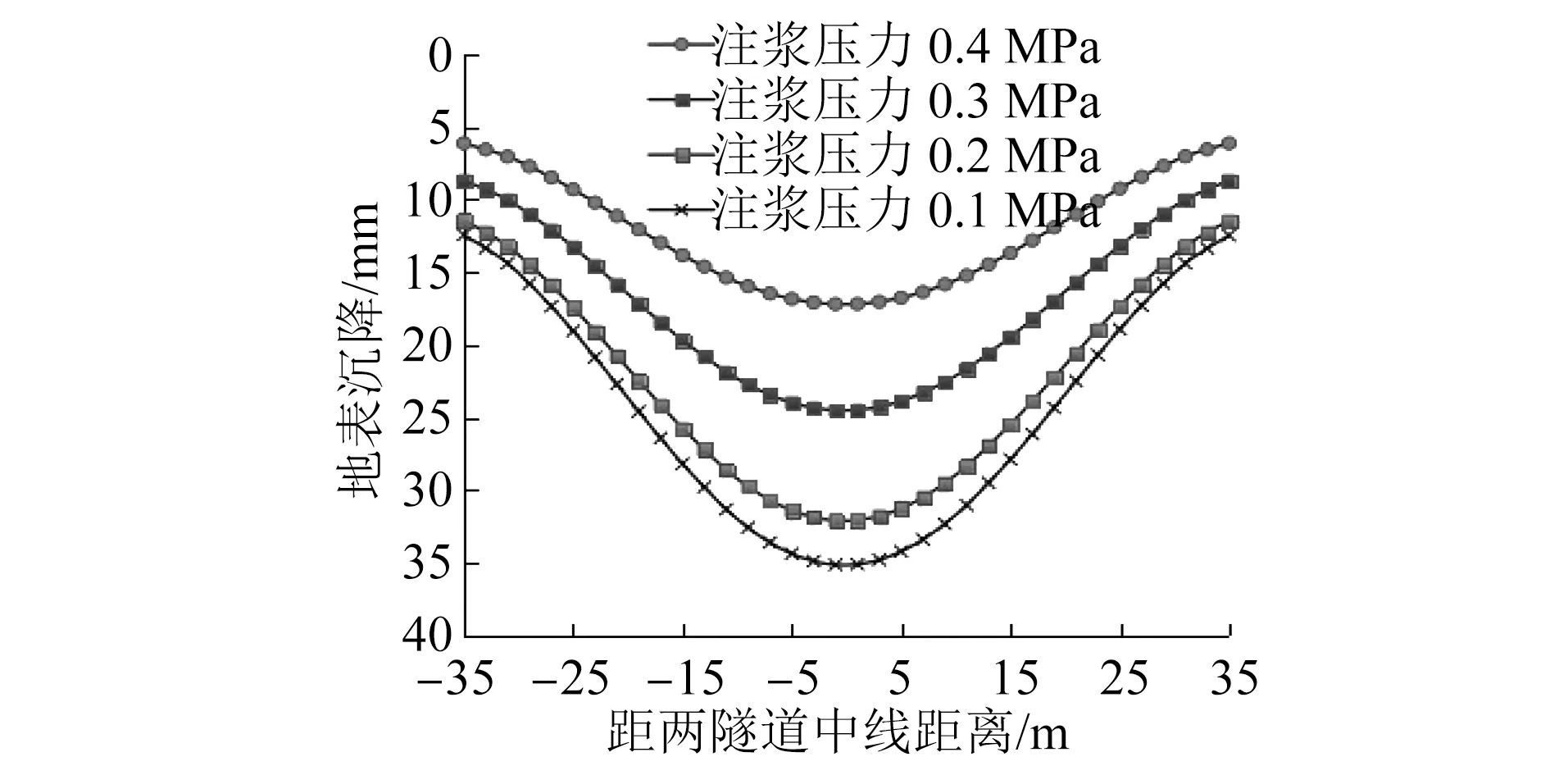
图6 不同注浆压力作用下地表沉降曲线
由图6可知,地表沉降值随注浆压力的增大而减小;当注浆压力为0.1 MPa时,地表最大沉降值为34.54 mm;当注浆压力为0.2 MPa时,地表最大沉降值为31.2 mm,较注浆压力为0.1 MPa时减小了9.6%;当注浆压力为0.3 MPa时,地表最大沉降值为23.97 mm,较注浆压力为0.2 MPa时减小了23.2%;当注浆压力增大到0.4 MPa时,地表最大沉降值为16.12 mm,较注浆压力为0.3 MPa时减小了32.7%。随着注浆压力的增大,其对于地表的沉降控制效果也越来越显著。但注浆压力增大会造成浆液浪费而导致成本增加,且还会引起管片上浮问题,严重影响施工的安全性。本工程中注浆压力为0.3 MPa和0.4 MPa时,地表沉降值均在合理范围内,故从节约成本等角度综合考虑,建议施工时选用0.3 MPa的注浆压力。
3 二次注浆对地表沉降控制效果的影响
3.1 二次注浆数值模拟效果
针对盾构下穿既有建筑物区段,本文采用二次深孔加强注浆的措施对隧道进行加固。采用的计算模型是在图2的基础上,根据实际的加固方案,通过预先埋设的注浆管道对隧道周边的土体进行二次注浆。计算模型如图7所示。
图7 注浆加固后的计算模型
根据前述研究成果,模拟中采用工况4,即右线贯通后左线再行开挖的施工顺序。施工时,盾构参数设置如下:掌子面顶推力为0.25 MPa、注浆压力为0.3 MPa。在计算模拟施工过程中,同步注浆采取理想化模型,不考虑其浆液流失等问题。二次深孔注浆的浆液采用水泥-水玻璃双液浆。
图8为二次注浆加固前后监测线2处的沉降对比曲线。由图8可知,注浆加固后3条监测线处地表的沉降变化规律与未加固时基本一致;与二次注浆加固前监测线处的沉降槽相比,加固后上述位置沉降槽的深度与宽度均小于加固前,由此说明在盾构隧道施工过程中,二次注浆加固对地表的沉降有明显的控制作用。因为二次注浆加固后,隧道周围土体的强度得到了有效加强,且注浆过程中由于注浆压力的作用,隧道周围土层的密实度亦得到了提高,这就使土体的扰动得到了有效抑制。
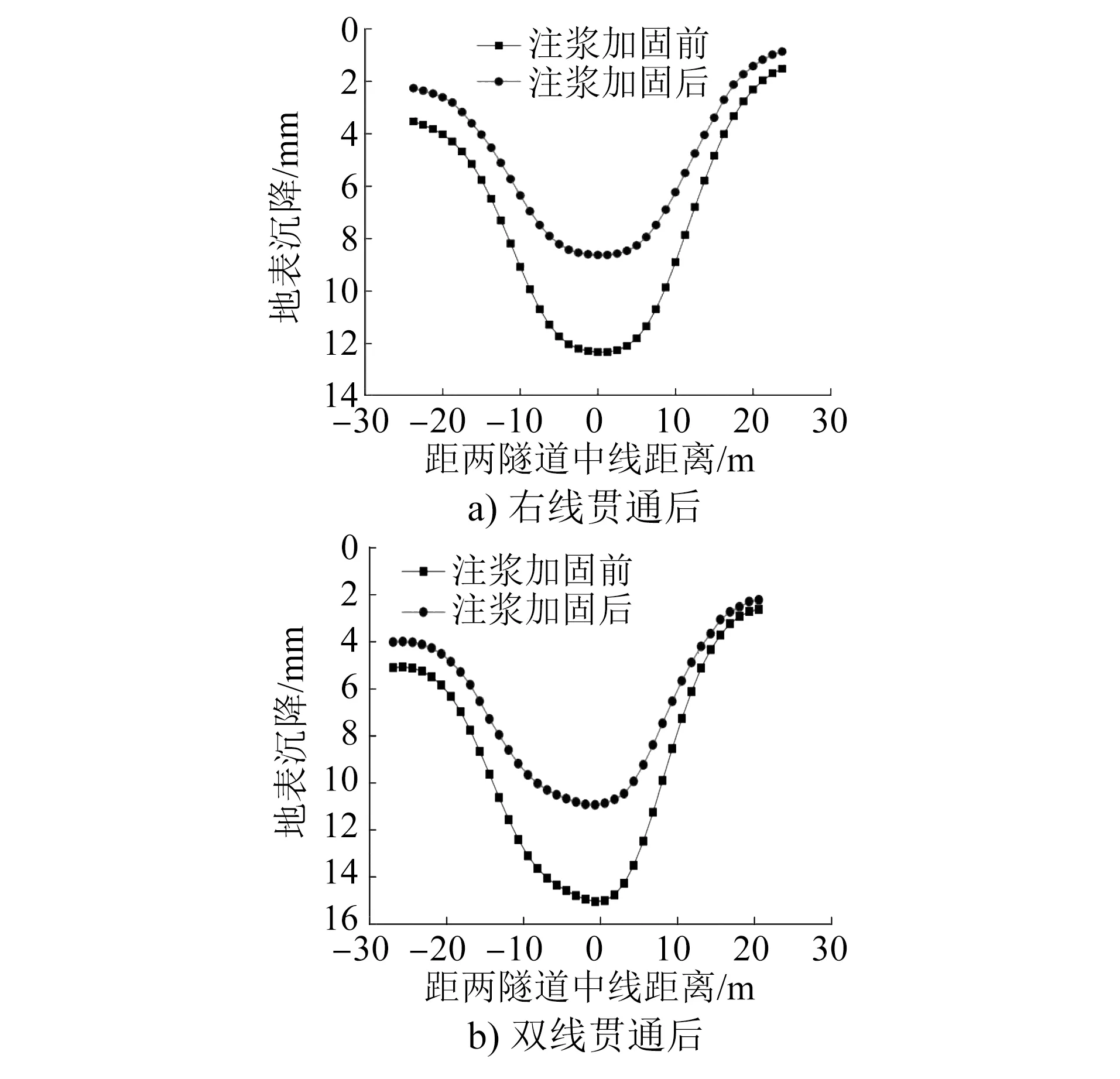
图8 二次注浆加固前后监测线2处的沉降对比曲线
二次注浆加固前右线贯通后监测线2处的地表沉降最大值为12.93 mm,二次注浆加固后地表沉降最大值为7.89 mm,较加固前减小了38.9%;二次注浆加固前双线贯通后地表沉降最大值为15.23 mm,二次注浆加固后地表沉降最大值为11.25 mm,较加固前减小了26.1%。由此可见,二次注浆加固后地表沉降值控制在12 mm的安全范围以内,因此二次深孔注浆的加固效果显著,达到了预期效果。
3.2 地表沉降现场监测数据与数值模拟数据对比
将二次注浆后地表沉降的现场监测数据与数值模拟数据进行对比分析,如图9所示。
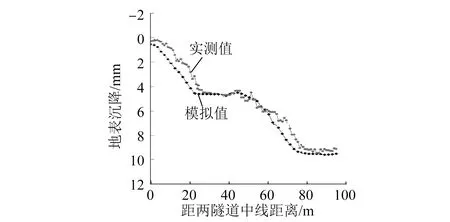
图9 二次注浆后JZ6监测点c处的地表沉降模拟值与监测值对比曲线
由图10所示地表监测线2处的沉降曲线可知,其数值模拟值与现场监测值的变化规律基本相同,呈喇叭状开口;监测线上地表沉降最大值出现在两隧道中线附近;地表沉降现场监测值大于数值模拟值,这是因为使用计算机软件进行模拟时,各种假定条件均较为理想化,且所建立的模型与实际存在差异,因此导致两者的最终结果存在偏差,但总体上该偏差仍处于可接受范围内。
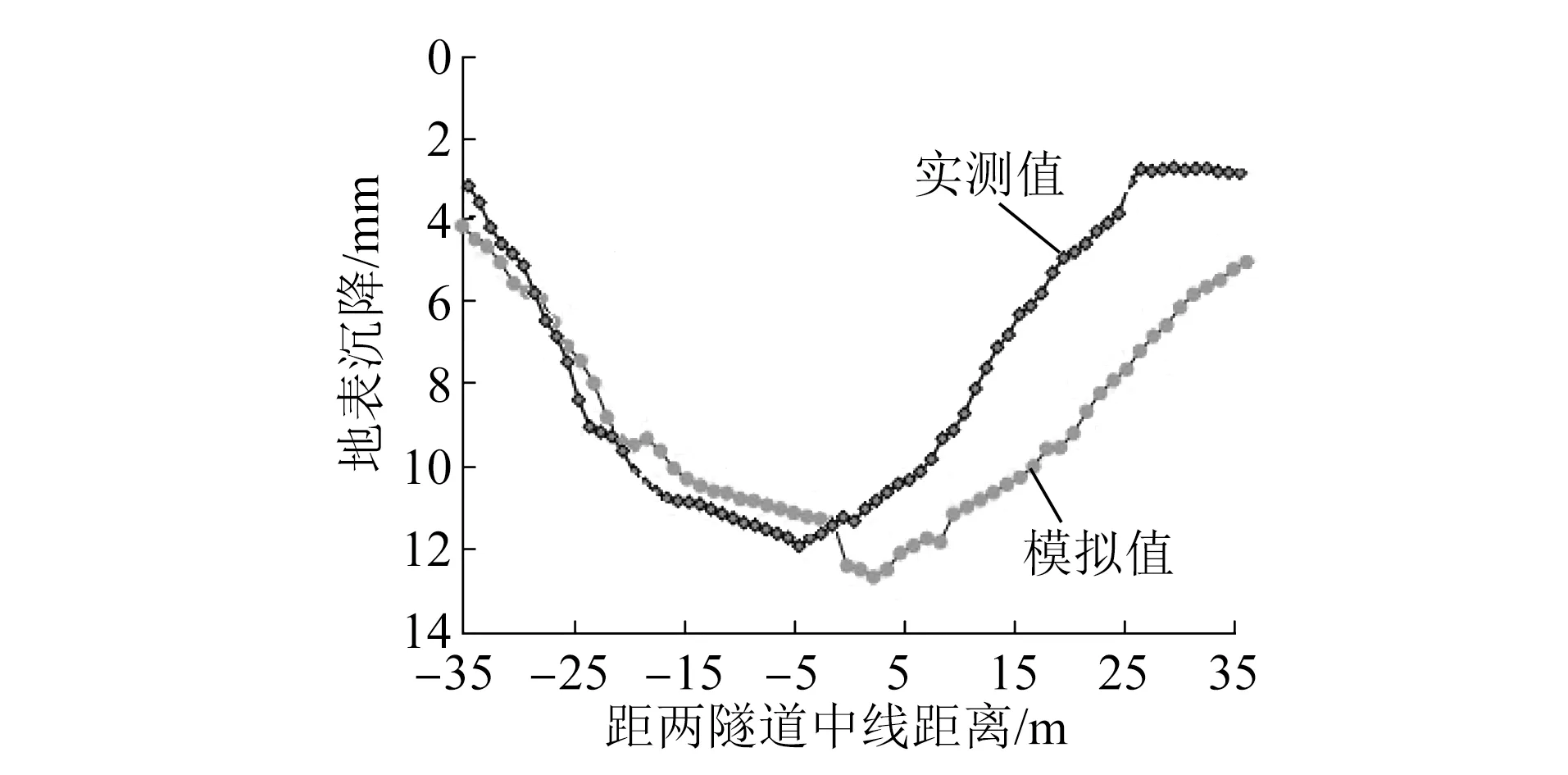
图10 二次注浆后监测线2处的地表沉降模拟值与监测值对比曲线
4 结论
1) 双线盾构隧道施工时,左右两线的施工间隔对于地表沉降有一定影响。双线施工间隔越大,对于地表的沉降叠加效应越小,地表的竖向变形越容易控制。故在盾构隧道施工时,选择右线贯通后左线再行施工的方案。
2) 随着掌子面顶推力与注浆压力的增大,地表的最大沉降值会相应减小。但当掌子面顶推力太大时,不仅会引起掌子面前方地表严重隆起,还会使刀盘磨损更快,增加施工成本;当注浆压力过大时,会产生管片上浮等不利情况。经综合考虑,建议施工时掌子面顶推力取0.25 MPa、注浆压力取0.30 MPa。
3) 对地表沉降的现场监测结果与数值模拟结果进行对比分析发现,虽然现场监测结果整体上大于数值模拟结果,但两者间的偏差仍处于可接受范围内,表明了数值模拟的可行性。

