配备主动减振器的车辆道路模拟试验研究
孙 野, 于长清, 王震伟, 刘志远,张子双, 杜 书
(1.中国第一汽车股份有限公司研发总院,长春 130013;2.汽车振动噪声与安全控制综合技术国家重点实验室,长春 130013)
道路模拟试验可以快速、有效地对车辆进行耐久性考核,其具有试验周期短、试验重复性好等优点,目前已被众多整车生产厂家所采用[1-3].
车辆在设计时,要求具有一定的平顺性和操稳性[4],为使车辆具有更好的性能,很多高端车型配备主动减振器,该减振器会根据车辆行驶的路况自动进行减振器阻尼调节,进而调整悬架软硬.
由于具备主动减振器的车辆在行驶过程中采用全时主动减振控制方式,按照传统道路模拟试验方法,难以对具备主动减振器的车辆进行试验,需要在试验中增加主动减振器控制环节,以实时控制主动减振器的阻尼特性,使其符合车辆在试验台架上振动状态所要求的阻尼特性,进而完成道路模拟试验.
1 试验方法
1.1 主动减振器控制
悬架电子控制单元(ECU,Electronic Control Unit)根据车速、发动机转速和扭矩、车身加速度、车身高度等一系列信号数据对车辆行驶状态进行判断,并对主动控制阀输出控制指令,控制阀门开度以提供适应当前行驶状态的阻尼特性.
基于主动减振器控制原理,文中通过配置dSPACE的CAN报文仿真模块建立硬件在环仿真系统,利用Simulink建立系统仿真模型,设置CAN报文收发接口,经编辑和编译后下载仿真程序到目标机,实现将车辆CAN信号数据传输给悬架ECU,经ECU计算后输出相应的控制指令给主动减振器,进而实现对减振器阻尼的实时控制.
1.2 道路模拟试验
配备主动减振器的车辆道路模拟试验的基本流程及控制方法如图1所示.

图1 主动减振器车辆道路模拟试验方法
文中基于MTS 329设备,对采用主动减振器的车辆进行道路模拟试验.采集汽车试验场典型工况载荷谱,同步采集车辆行驶过程中的CAN报文;应用粉红噪声信号驱动整车与台架系统运行,求解系统频响函数[5-9];对主动减振器车辆进行迭代,迭代过程中,为悬架ECU发送CAN报文[10],CAN报文的发送需与载荷驱动信号实时同步,保证减振器阻尼状态与车辆振动状态相一致.
2 数据采集及处理
2.1 载荷测点选取
在整车道路模拟试验中,应用非方阵迭代法能够有效地保证迭代准确度,选取悬架中部分零部件载荷、轴头加速度、悬架位移信号等参与迭代,可使道路模拟试验中悬架零部件所受载荷与路试时更加接近,保证车身运动姿态相一致[11].
综合考虑试验,重点关注零部件及悬架各部件在车辆行驶时的受力情况,选取的测点需尽量与车轮受到的纵向力、侧向力、垂向力中的某一方向力相关性高,而受其它方向力的干扰较小,保证测点与单一方向力相关性高,有利于迭代的收敛,提高迭代准确度.文中采集的信号及所用传感器见表1所示.
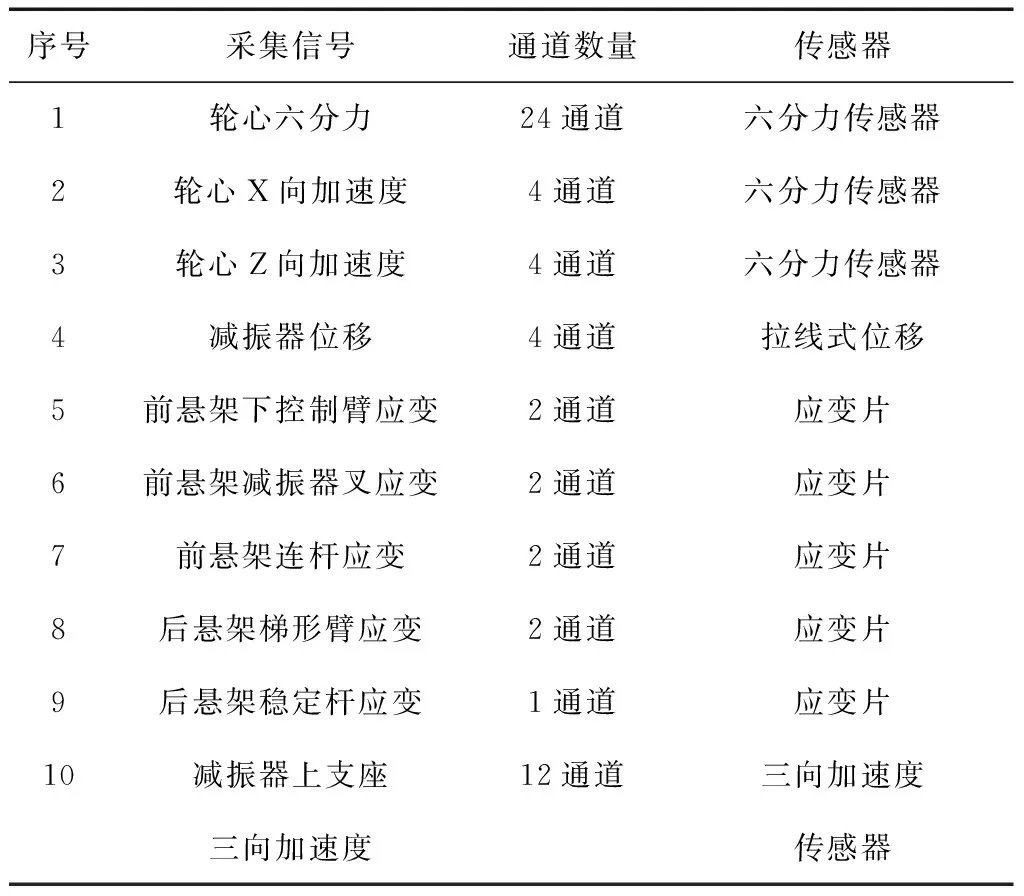
表1 采集信号与传感器
2.2 CAN报文采集
在载荷谱采集过程中,需通过车辆CAN总线同步采集悬架CAN报文信息,CAN报文需与载荷谱信号实时对应.
2.3 典型工况
试验中采集的典型工况及车速如表2所示.

表2 典型工况与车速
3 频响函数求解与迭代
3.1 试验系统
道路模拟试验系统为多输入、多输出系统,系统模型如图2所示.其中:X(ω)为系统输入信号矩阵;Y(ω)为系统输出信号矩阵;H(ω)为系统的频响函数矩阵.
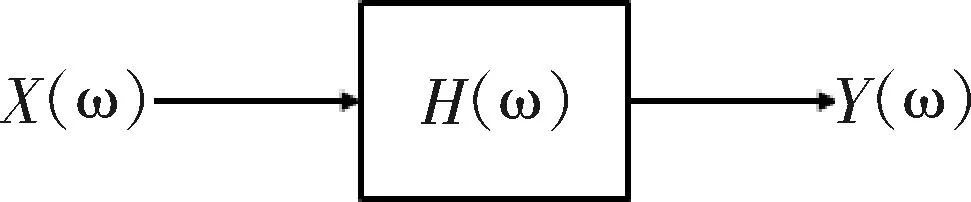
图2 多输入、多输出试验系统
忽略试验系统中非线性因素的影响,把整个系统简化为线性时不变系统,则频响函数矩阵H(ω)计算方法为
H(ω)=Gyx(ω)/Gxx(ω),
(1)
式中:Gyx(ω)是输出与输入信号互功率谱密度(dB);Gxx(ω)是输入信号自功率谱密度(dB).
进行系统频响函数求解时,应用粉红噪声信号激励系统运行,各传感器采集响应信号,根据式(1)计算得到系统频响函数矩阵H(ω).
3.2 粉红噪声激励信号
3.2.1 能量分布
粉红噪声的能量主要分布于中低频段,其能量随着频率的增加而降低,功率谱密度与频率成反比,应用粉红噪声驱动系统可有效求解出系统频响函数.文中生成粉红噪声能量分布在[0,50 Hz]频率范围,所生成的左前轮垂向激励信号功率谱密度曲线如图3所示.
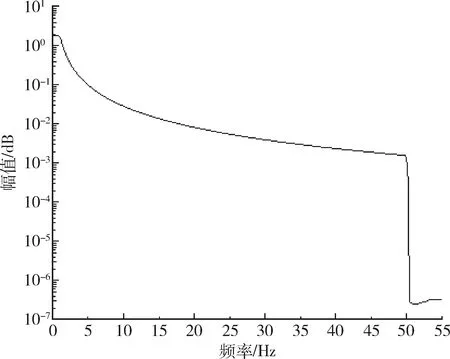
图3 左前轮垂向粉红噪声激励功率谱密度
3.2.2 幅值分布
生成的粉红噪声激励信号幅值分布服从N(0,σ2)的高斯分布,依据“3σ”原理,在高斯分布下,落在[-3σ,3σ]区间的幅值占比为99.7%,所以,在设定粉红噪声信号幅值时,主要给3σ进行赋值,并且要求用给定的幅值所生成的粉红噪声信号激励系统运行后,得到的响应信号最大值应介于目标信号最大值的20%~100%之间.文中生成的左前轮垂向粉红噪声激励信号给定的3σ值为6,幅值高斯分布图如图4所示.
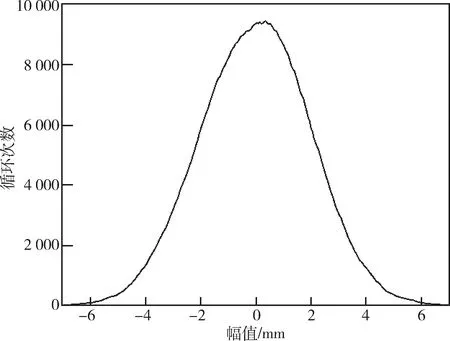
图4 左前轮垂向粉红噪声激励幅值高斯分布图
3.3 频响函数求解
频响函数表征了试验系统在各频率下的系统特性,主要指输出信号、输入信号幅值比与频率的函数关系,和输出信号、输入信号相位差与频率的函数关系,频响函数直观反映了试验系统对各频率输入信号的响应特性.
在求解系统频响函数时,为使控制指令所控制的主动减振器阻尼状态符合频响函数求解时粉红噪声驱动车辆过程中车辆的振动状态,依据车辆运动状态,通过硬件在环仿真系统为电控悬架ECU发送特定的仿真CAN报文信号,此CAN报文信号经ECU计算后,ECU为主动减振器发送控制指令,控制减振器阻尼达到期望状态.
3.4 迭代
由于系统非线性的存在,无法通过线性计算准确预测输入信号,需要通过迭代使台架响应信号不断趋近期望响应信号.迭代过程中,依据前文1.1所述的方法实时控制主动减振器阻尼状态,使其与车辆振动状态相匹配.
迭代初始时,应用系统频响函数H(ω)和期望响应Yd(ω),计算频域初始驱动信号X0(ω)为
X0(ω)=diag(α)[H(ω)-1Yd(ω)],
(2)
式中:α为步长系数,取值范围[0.01,1].通过α可以控制每一步迭代的步长,即控制响应信号趋近于期望响应速度的快慢,迭代初始阶段,由于与期望响应信号差距较大,α取值不宜过大,过大的取值可能会使迭代发散,应随着迭代的不断进行,响应信号与期望响应信号误差逐渐缩小,逐步加大α的取值.
频域初始驱动信号X0(ω)经过傅里叶逆变换,得到初始驱动信号X0(t).用初始驱动信号X0(t)驱动试验系统运行,得到第1次响应信号Y1(t),依次进行迭代,假设第i次响应信号为Yi(t),则响应信号Yi(t)与期望响应信号Yd(t)的时域误差ΔYi(t)为
ΔYi(t)=Yd(t)-Yi(t).
(3)
对ΔYi(t)进行傅里叶变换,可得频域响应误差ΔYi(ω).计算第i次频域驱动信号修正ΔXi(ω)为
ΔXi(ω)=H(ω)-1ΔYi(ω).
(4)
频域驱动信号修正ΔXi(ω)经过傅里叶逆变换得到驱动修正信号ΔXi(t),修正后的驱动信号Xi(t)为
Xi(t)=Xi-1(t)+diag(α)ΔXi(t).
(5)
当由Xi(t)驱动系统运行得到的响应信号与期望响应信号误差满足试验要求时,迭代结束.
3.5 迭代误差
每一步迭代中,应用台架响应信号相对期望响应信号的均方根误差对迭代准确度进行评价,可以直观地了解到迭代收敛情况,有助于分析响应信号与期望响应信号的偏差,一般,迭代误差越小,代表迭代收敛情况越好,道路模拟试验准确度越高.均方根误差Err计算方法为
(6)
经过一定迭代次数,信号逐渐收敛,迭代误差趋于稳定,部分典型工况迭代次数及迭代误差见表3.由表3可知,前轮轮心载荷迭代误差均在20%以下,收敛效果较好,符合试验要求.

表3 部分典型工况迭代误差
4 一致性分析
对迭代后的台架响应与期望响应,分别从时域、频域和相对损伤3个方面进行一致性分析[11].
4.1 时域分析
图5(a)、(b)所示分别为鱼鳞坑路工况的车辆右后轮Fz台架响应与期望响应的时间历程曲线,表4所示为鱼鳞坑路工况的车辆右后轮Fx、Fy、Fz载荷台架响应与期望响应的统计量对比.由图5和表4可知,台架响应与期望响应在最大值、最小值、标准差等统计量的数值差距较小,误差均在5%以内,信号时域特征表现基本一致.
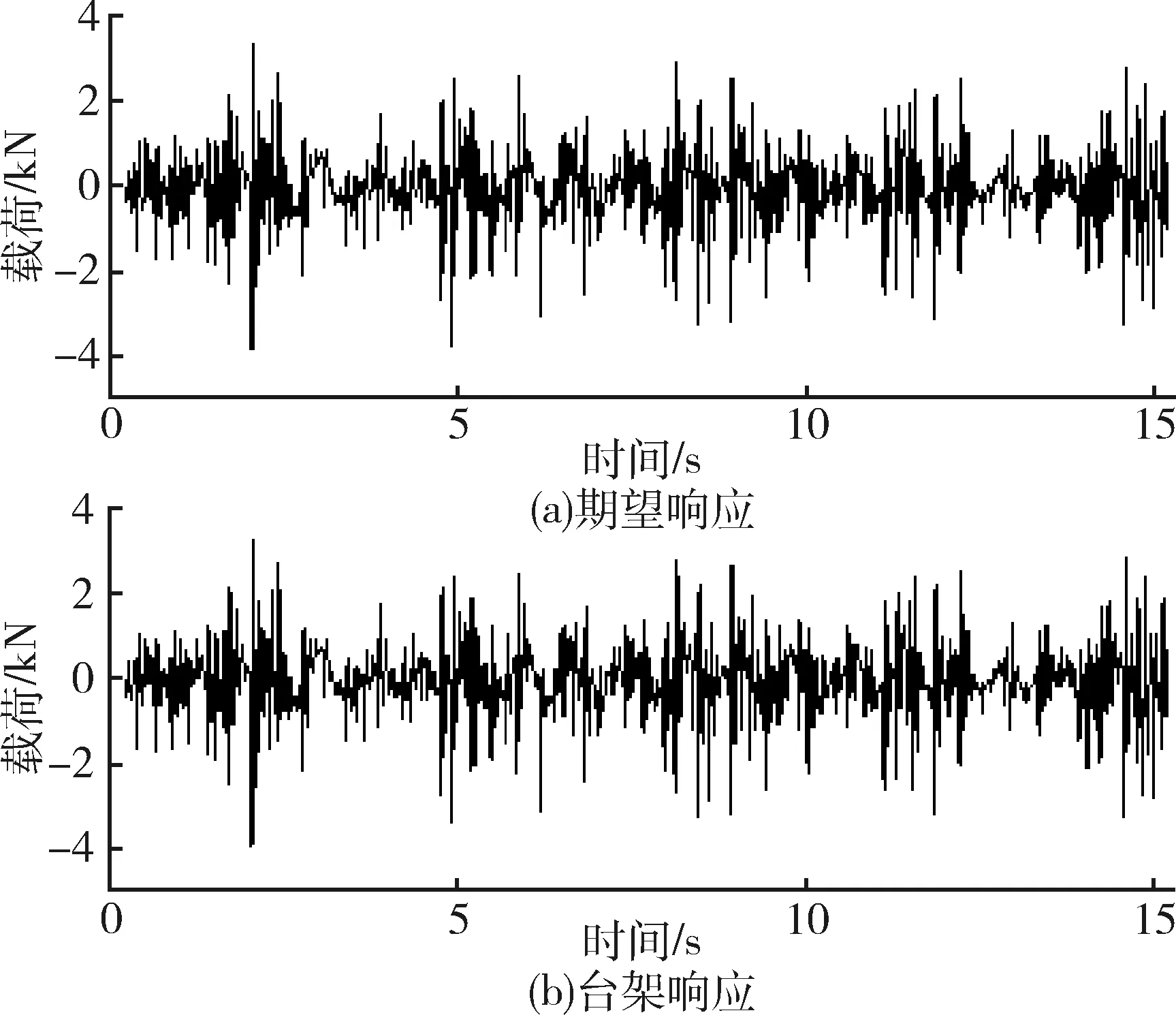
图5 期望响应与台架响应时间历程曲线

表4 期望响应与台架响应统计量
结果表明,通过发送CAN报文对主动减振器车辆进行迭代,所得台架响应信号与期望响应信号的载荷统计量一致性较好,道路模拟试验较好地再现了车辆在实际道路上的动态时域响应特性.
4.2 频域分析
利用功率谱对台架响应与期望响应进行分析,其主要表征了零部件在相应频率范围内吸收能量的大小.图6所示为鱼鳞坑路工况车辆右后轮Fz台架响应与期望响应在[0,50 Hz]范围内的功率谱密度曲线.由图6可知,台架响应与期望响应功率谱密度峰值及对应频率基本相同,能量分布基本一致.

图6 期望响应与台架响应功率谱密度
结果表明,迭代后的台架响应与期望响应在频域上的能量分布一致性较好,道路模拟试验较好地再现了车辆在实际道路上的频域响应特性.
4.3 疲劳损伤分析
依据帕姆格伦-迈因纳(Palmgren-Miner)线性疲劳损伤累计理论,计算台架响应与期望响应完成相同工况耐久试验循环数时的伪损伤.表5为车辆右后轮部分测试通道期望响应与台架响应的伪损伤,图7为车辆右后轮部分测试通道台架响应与期望响应伪损伤对比.由表5可知,各测试通道台架响应与期望响应伪损伤数值处于相同数量级,数值差距较小;由图7可知,各测试通道台架响应与期望响应伪损伤比值均在[0.8,1.6]区间范围内,满足疲劳耐久试验要求.
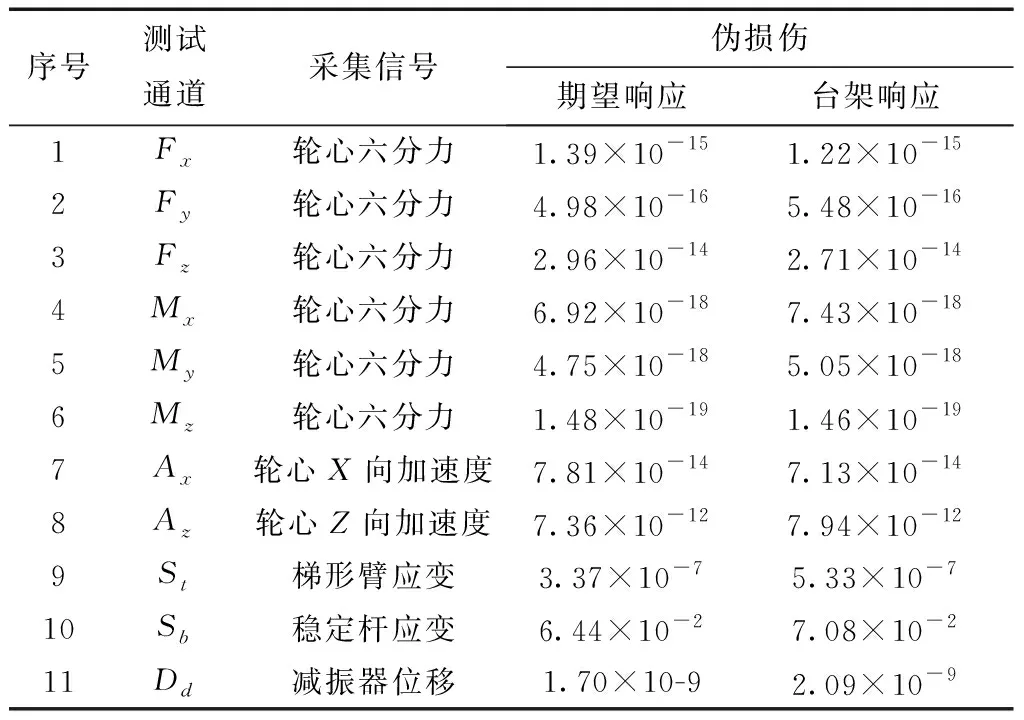
表5 期望响应与台架响应伪损伤

图7 台架响应与期望响应伪损伤对比
结果表明,迭代后的台架响应与期望响应伪损伤一致性较好,道路模拟试验有效地复现了车辆在实际道路上的疲劳耐久特性.
5 主动减振器控制与非控制状态迭代响应信号对比
为进一步说明主动减振器在控制与非控制状态下,迭代响应信号之间的区别,文中对车辆处于两种状态时分别进行迭代,对比两者迭代响应信号与期望响应信号的时域重合度和迭代误差,分析车辆处于两种条件下时的迭代收敛情况.
5.1 时域对比
迭代后的台架响应与期望响应在时域的重合情况,直接反映了迭代准确度.主动减振器控制与否,主要影响悬架垂向运动,在采集的响应信号中,减振器位移信号表征了悬架垂向运动状态,间接反映出减振器是否处于正确的阻尼状态.如图8所示,为铁路工况下主动减振器控制与非控制时减振器位移信号的时域对比情况.

图8 位移信号时域对比
从图8中可以清楚看到,主动减振器在控制状态下,位移信号与期望响应基本重合,证明减振器阻尼特性与路试时一致;而在非控制状态下,即ECU不为减振器发送控制指令时,减振器阻尼为偏硬的阻尼特性,所以图中非控制状态位移信号比期望响应幅值偏小,误差较大.
5.2 迭代误差对比
从迭代误差收敛趋势上,亦可看出主动减振器在控制与非控制条件下收敛情况的差别,同样以铁路工况为例,对车辆处于两种状态下迭代时,应用相同的频响函数,且迭代的步长系数相同,如图9所示,为主动减振器在控制与非控制条件下后轮减振器位移的迭代误差对比图.从图中可知,主动减振器非控制状态时,位移误差较大,该信号通道完全不收敛;而在主动减振器给予正确控制时,位移误差较小,收敛效果好.
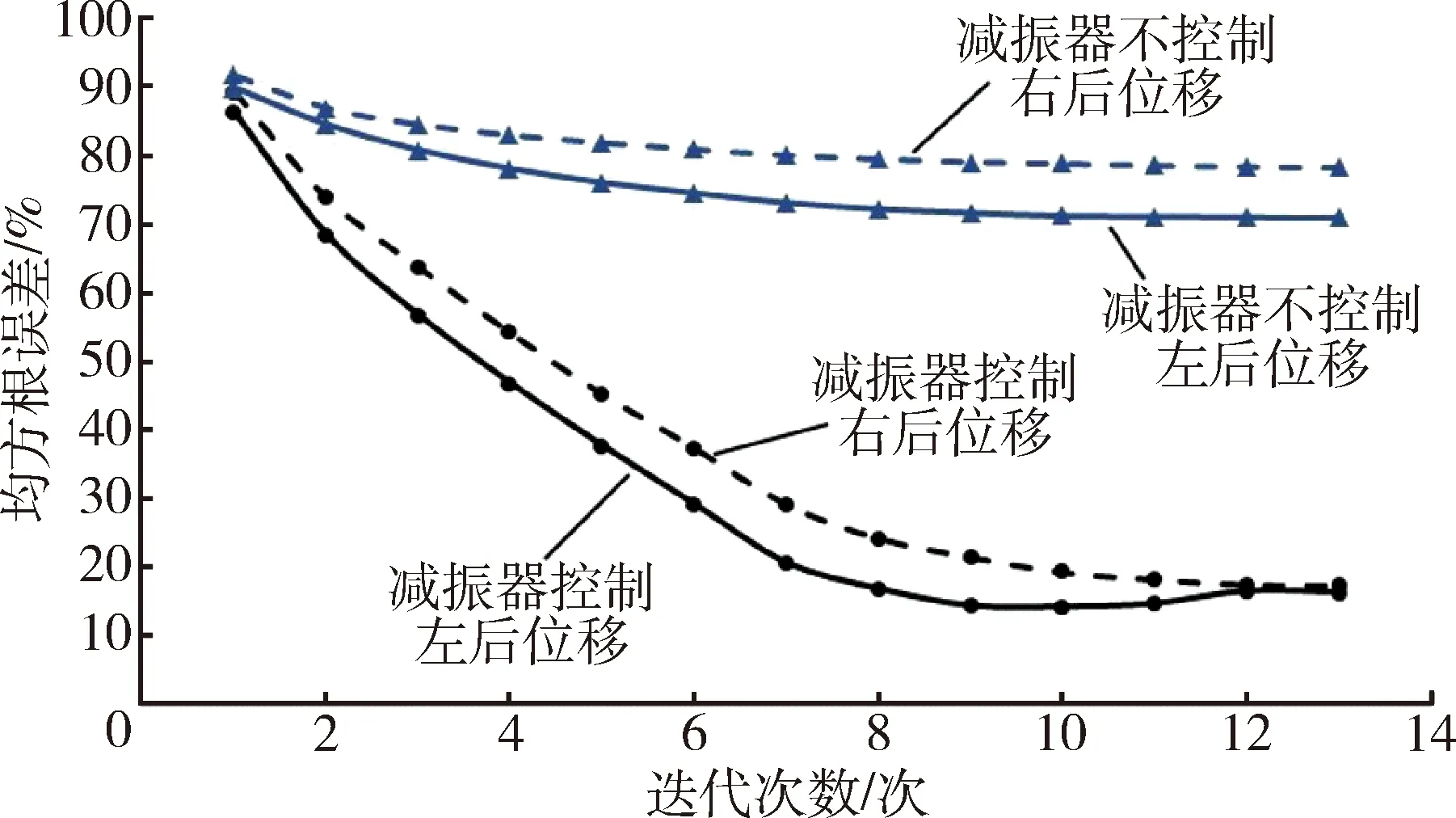
图9 位移迭代误差对比
6 结 论
文中通过将CAN报文发送给悬架ECU,由ECU计算并为主动减振器发送控制指令,控制主动减振器阻尼状态,同时,保证CAN报文的发送与载荷谱信号实时同步,使主动减振器阻尼状态与车辆振动状态相符,求解系统频响函数,对配备主动减振器的车辆进行迭代,并对迭代后的台架响应信号与期望响应信号进行时域、频域和伪损伤的一致性分析,通过对比主动减振器控制与非控制状态下迭代后的台架响应信号,分析时域信号重合度与迭代误差,证明CAN报文仿真控制主动减振器的方法能够有效对配备主动减振器的车辆进行道路模拟试验.

