双电机耦合驱动电动汽车传动系统扭转振动特性分析
岳宏伟, 何洪文
(北京理工大学 机械与车辆学院,北京100081)
汽车传动系统的扭转振动与汽车的舒适性和安全性直接相关.在严峻的环境资源问题和日益严格的排放法规背景下,清洁高效的新能源汽车成为汽车领域的研发重点之一,其中纯电动汽车、混合动力汽车的研发和应用相对广泛.与传统汽车相比,电动机成为了电动汽车的主要动力源之一,相比于内燃机,电动机具有相对较快的转矩动态响应、较宽的转速调节范围和较高的转矩波动频率,并且电动汽车的传动系统结构表现出低阻尼特征,这些变化使电动汽车传动系统的扭转振动呈现出了新的特点,其NVH问题值得进行深入分析和研究.
Tang等[1]提出了一种简化扭转振动动力学模型,用于研究某混合动力汽车的扭转振动特性.仿真结果证明该简化模型能够准确描述传动系统的低频振动特性.Hu等[2]建立了传动系统瞬态动力学模型,对电动汽车机械系统和电气系统之间的相互作用进行了仿真和分析并提出了一种主动阻尼控制策略.王欢等[3]建立了包含电磁刚度的两自由度电动汽车电驱动系统的动力学模型,并通过一系列的振动台架试验,分析了电驱动系统的振动特性.张元元等[4]分析了某集中式驱动电动汽车的固有特性,建立了驱动电机和动力传动系统的机电仿真模型,分析了电机参数对传动系统灵敏度的影响.刘必华等[5]建立了某纯电动汽车的集中质量模型,分析了传动系的固有特性和模态振型,并基于灵敏度分析结果提出了传动系统的优化方案.
从上述文献中可以看到,目前对于汽车传动系统扭振问题的研究,主要针对传统燃油车、单电机驱动的纯电动汽车或混合动力汽车等构型.由于电动机和内燃机具有不同的特点,对于双电机耦合驱动且同时包含定轴与非定轴结构的传动系统,其扭振问题值得进行更加深入的讨论.本文以某双电机耦合驱动构型的洗扫车为研究对象,以集中质量法建立传动系统扭振模型,基于振动理论分析其固有频率及振型,基于电机控制理论计算该构型在C-WTVC工况下的临界车速点.在Matlab/Simulink环境下建立传动系统强迫振动模型,对其强迫振动动态响应进行仿真分析.探究了双电机耦合驱动的复杂传动系统的扭振特性,并进一步研究了电机转矩变化率对汽车动力性损失和减振效果的影响.
1 建立传动系统扭振模型
1.1 整车传动系统扭振模型简化原则
本文研究的对象为某纯电动洗扫车的传动系统构型,其中包括驱动电机、作业电机、两挡变速箱、行星排以及主减速器、半轴、车轮等,传动系统总成,如图1所示.
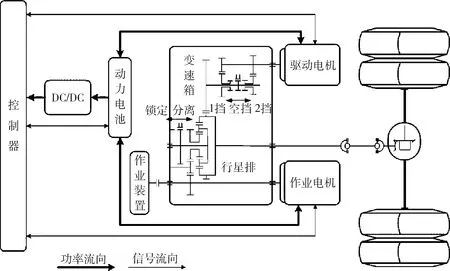
图1 双电机耦合驱动传动系统构型图
在实际的动力传动系统总成中,质量和弹性分布不均匀,为便于分析,本文采用集中质量模型对传动系统进行简化,简化原则如下[6]:
1)根据传动系统中各组成部分的惯量和弹性大小,将其考虑为弹性元件或质量元件;
2)忽略加工过程中的加工制造误差和装配误差,认为齿轮啮合刚度在传动过程中恒定,忽略系统间隙的影响以及差速器的差速作用;
3)不考虑系统中的弯曲振动和拉压振动;
4)认为传动系统为线性系统,忽略其非线性特性.
1.2 建立无阻尼自由振动模型和强迫振动模型
传动系统经过简化后得到无阻尼自由振动模型如图2所示.图中,变量Jm1、Jm2、J1、J2、J3、J4、J5、JS、JPi、JR、Jd1、Jd2、Jt1、Jt2、Jv分别代表驱动电机、作业电机、变速箱主动齿轮、变速箱从动齿轮、变速箱输出齿轮、作业电机输出齿轮、惰轮、太阳轮、各行星轮、齿圈、主减速器主动齿轮、主减速器从动齿轮、左车轮、右车轮和整车的等效转动惯量;图中,变量θ代表各质量元件的角位移,其下角标表示质量元件的位置,含义与变量J的下角标一致;变量k代表两个相邻质量元件之间轴段的扭转刚度或齿轮间的啮合刚度.
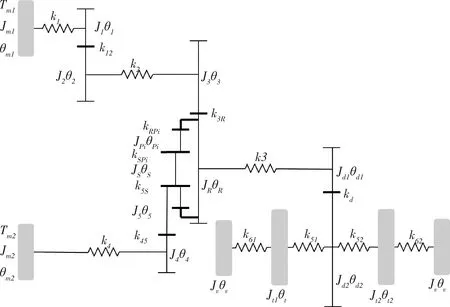
图2 双电机耦合驱动传动系统扭振模型图
振动系统中各部件的动力学方程可根据式(1)建立.
(1)
式中:Ji表示第i个部件的转动惯量,kgm2;Tin和Tf分别表示对应部件受到的输入转矩和阻力矩,Nm.
基于上述动力学关系对振动系统各部分建立动力学方程,并整合为振动矩阵,如式(2)所示.
(2)
式中:M为17×17的等效质量矩阵;K为17×17的等效刚度矩阵;X为广义位移向量,可表示为:
X={θm1θ1θ2θ3θm2θ4θ5θSθPiθRθd1θd2θt1θt2θv}T.
(3)
以无阻尼自由振动数学模型为基础,在MATLAB/Simulink环境中建立强迫振动模型,以进一步分析传动的动态响应.模型中相关的阻尼系数由以下公式计算.
轮齿啮合阻尼系数[6]
(4)
式中:εv为啮合阻尼比;kv为齿轮副啮合刚度;rb1、rb2为主、从动齿轮的基圆半径;J1、J2为主、从动齿轮的转动惯量.
轴的扭转阻尼系数为[6]
(5)
式中:
εT为扭转阻尼比;kT为轴的扭转刚度;J1、J2为轴两端部件的转动惯量.
2 传动系统扭转振动特性分析
2.1 传动系统的固有频率和振型
通过求解动力传动系统特征方程,能够得到传动系统的固有频率以及对应的模态振型,一挡和二挡对应的各阶固有频率如表1所示.
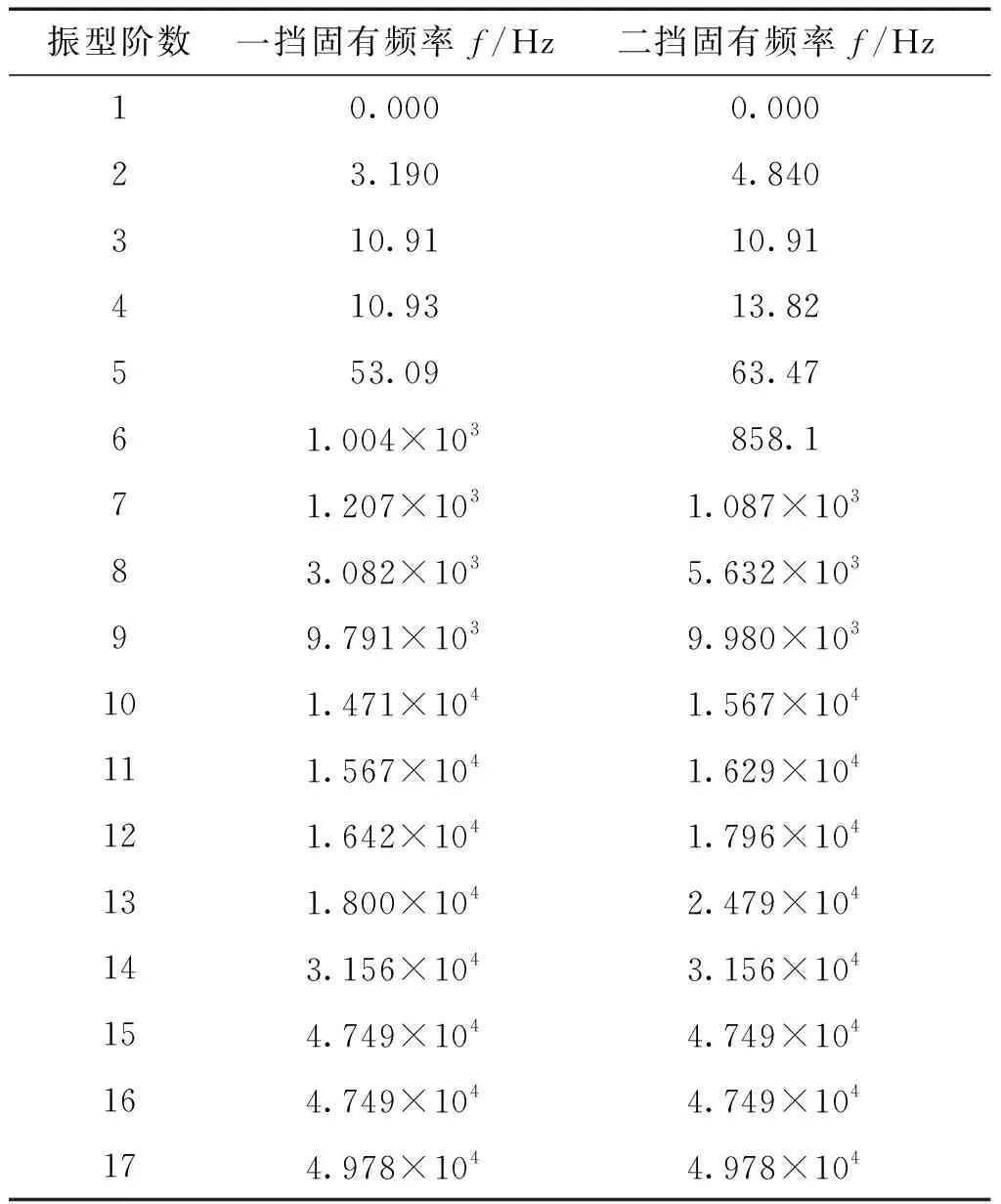
表1 传动系统扭振固有频率
将模态振型归一化,得到车辆在一挡、二挡时动力传动系各阶模态振型如图3所示,其中,节点1至节点17分别代表着驱动电机、变速箱主动齿轮、变速箱从动齿轮、变速箱输出齿轮、作业电机、作业电机输出齿轮、惰轮、太阳轮、各行星轮、齿圈、主减速器主动齿轮、主减速器从动齿轮、左车轮、右车轮、整车.

图3 各挡模态振型图
归一化后的模态阵型图准确直观地表现了各阶固有频率下传动系统各部件的相对振幅关系.由图3分析可知,汽车分别在一挡和二挡行驶时,其各阶模态振型的总体特征基本一致.从整体上看,在低阶频率段,1阶固有频率对应刚体模态,2阶模态下传动系统中各部件相对振幅均较大,3、4阶模态下的相对振幅较大的位置则主要出现在车轮处;在中间阶频率段,最大相对振幅主要出现在变速箱及主减速器处;在高阶频率段,最大相对振幅主要出现在行星排的位置.仿真结果比较符合常识,验证了仿真分析的有效性.
2.2 电机临界转速及共振点分析
在本文研究的传动系统中,驱动电机的输出转矩是主要的激励源,当电机转矩中的某谐波分量接近传动系统的固有频率时,将发生共振现象.共振时的电机临界转速的计算公式如式(6)所示[7].
(6)
式中:nc表示电机临界转速,r/min;f表示传动系统扭振的固有频率,Hz;k表示电机转矩波动中的谐波转矩频次.
文中采用的永磁同步电机具有4对极,且其电磁转矩的谐波转矩频率为电频率的6倍,谐波阶数越高,谐波转矩的幅值会相应下降,故高阶谐波对传动系统扭振的影响可忽略不计[7].在工程问题中,可以只考虑低阶的谐波分量,本文选取前两阶谐波量,即取k值为24和48.
结合传动系统的固有频率,可得各挡对应的临界车速,如表2所示.

表2 各挡临界车速
对于纯电动汽车,其最低稳定车速一般在4~5 km/h,该洗扫车行驶工况为C-WTVC工况,结合表2可知,汽车在一挡和二挡行驶时,在C-WTVC工况的车速范围内,高于最低稳定车速的临界车速点各有8个.传动系统在对应的挡位和临界车速下将会发生共振,对行驶过程中的安全性和舒适性造成影响.
2.3 强迫振动动态响应分析
在强迫振动模型中,分别在驱动电机和作业电机处施加1 100 Nm和650 Nm的阶跃转矩模拟急加速工况,仿真时间为10 s;施加斜坡转矩模拟缓加速工况,设定驱动电机和作业电机的转矩上升时间均为1.1 s,最终达到的转矩分别为1 100 Nm和650 Nm,仿真时间为10 s.一挡和二挡时的传动系统强迫振动响应具有相似的特征,以一挡行驶为例进行强迫振动动态响应分析,仿真结果如图4所示.

图4 急加速工况和缓加速工况下强迫振动响应
由图4可知,在急加速工况下,传动系统出现了严重的扭振现象.电机轴处动载荷与整车的等效角加速度曲线出现明显抖动,驱动电机、作业电机、等效角加速度的超调量分别为83.92%、90.63%、105.68%,经过6 s之后逐渐趋于稳定.相较于急加速工况,缓加速工况的扭振现象明显改善,两电机轴处的动载荷以及整车等效角加速度的超调量分别为4.03%、2.27%和5.51%,并能够更快地达到稳定值.对比可知,减小电机转矩变化率能够使传动系统的瞬态扭振得到有效改善;但从汽车动力性的角度考虑,由图4(d)可知,限制电机的转矩变化率将会使汽车的速度响应滞后,对汽车的动力性造成负面影响.
为进一步研究电机转矩变化率与扭振响应及动力性能的关系,本文以一挡为例,分别设置驱动电机转矩变化率为1 000 Nm/s、2 000 Nm/s、4 000 Nm/s、8 000 Nm/s,为方便分析,设置作业电机的转矩上升时间与驱动电机一致.不同转矩变化率下传动系统的强迫振动仿真结果如图5所示.
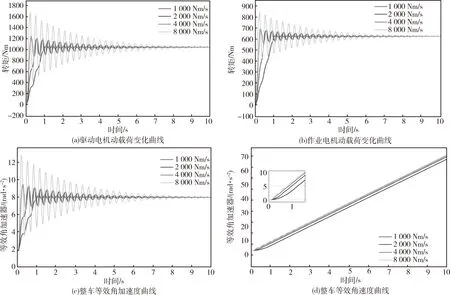
图5 四种电机转矩变化率下一挡扭振响应
表3列出了4种转矩变化率下扭振动态响应的超调量,当转矩变化率为1 000 Nm/s时,扭振动态响应的超调量很小;转矩变化率为2 000 Nm/s和4 000 Nm/s时,超调量有小幅增长;转矩变化率达到8 000 Nm/s时,超调量则大幅增加.对比等效角速度变化曲线可知,相较于8 000 Nm/s的转矩变化率,1 000 Nm/s时的速度响应滞后0.42 s, 2 000 Nm/s时滞后0.16 s,4 000 Nm/s时仅滞后0.05 s.结果表明,对电机转矩变化率进行控制,能够在保持动力性能的基础上实现较为显著的减振效果.
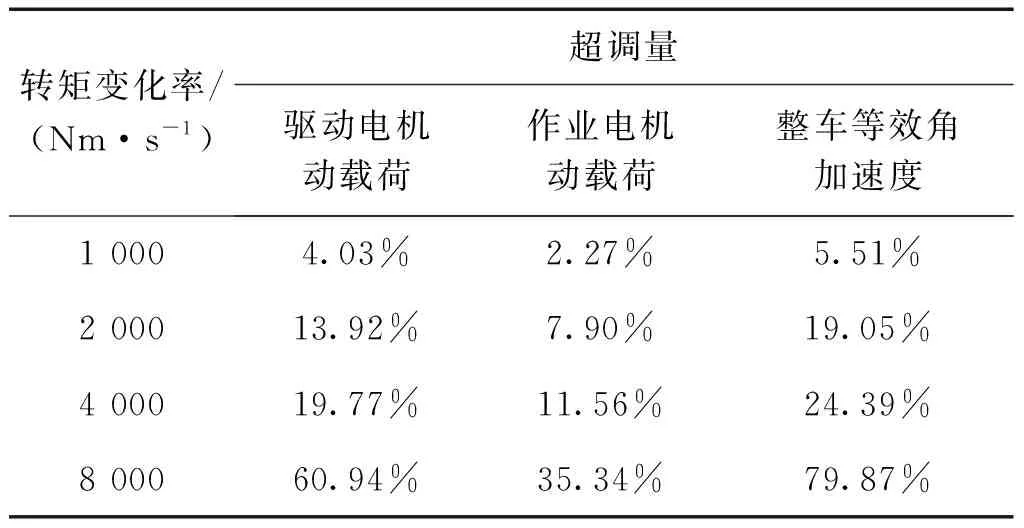
表3 不同电机转矩变化率下扭振动态响应超调量
3 结 论
文中根据传动系统构型和相关参数,建立了传动系统集中质量模型,求解无阻尼自由振动数学模型,得到传动系统的固有频率,通过对振型进行归一化处理,分析得到各挡位下传动系统各节点的相对振幅关系,并基于电机临界转速的计算结果,分析汽车行驶过程中的共振可能性,并找到一挡和二挡下各8个共振点车速,在MATLAB/Simulink环境下建立了强迫振动模型,对急加速和缓加速两种工况进行仿真,对扭振动态响应进行分析,结果验证了限制电机转矩变化率能够使汽车扭振现象得到明显改善,但会对动力性产生负面影响,并基于此结论进一步量化分析了电机转矩变化率对汽车动力性损失和减振效果的影响.

